[Из песочницы] Анализ аудио-кодека ROAD
Далее будут рассмотрены заявленные уникальные свойства и произведено несколько тестовых измерений.
Предпрослушивание
В статье описывается довольно сложная формула для объяснения этого свойства, но на самом деле всё намного проще. По факту это свойство означает, что компрессии подвергается не весь сигнал, а только его часть, что продемонстрировано на следующем изображении:
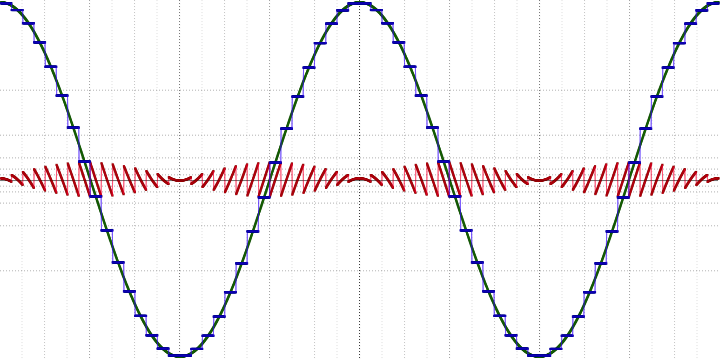
Здесь зелёным цветом помечен исходный сигнал, синим — усреднённый по некоторому количеству точек (семплов) и сохраняемый в явном виде, и красным — остаток, подвергаемый сжатию.
В сильно грубом приближении можно сказать, что сжимается лишь высокочастотная часть сигнала. Более точно в частотной области разделение на усреднённый и остаточный сигналы будут выглядеть, например, так (для 4-кратного усреднения в 48 кГц):
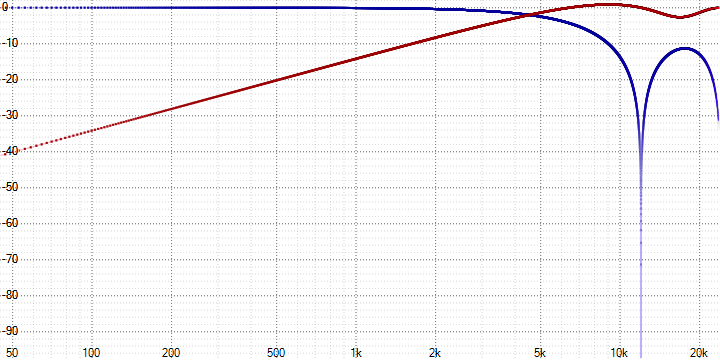
Или так (для 32-кратного усреднения в 48 кГц):

Ещё более точный вид будет зависеть от конкретного взятого сигнала. Например, для синусоиды из самого первого изображения:
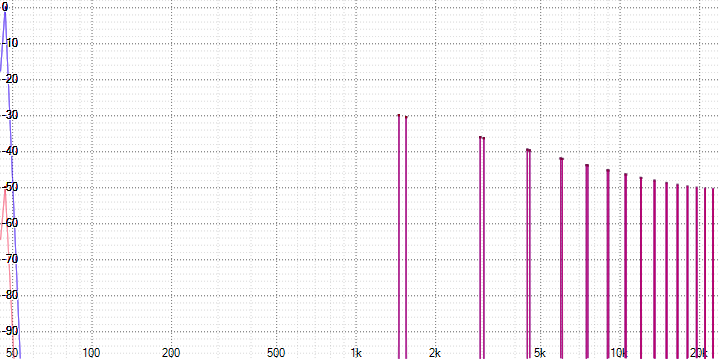
Здесь усреднение привело к появлению гармоник в противофазе в обоих сигналах, которые взаимокомпенсируются при сложении. Очевидно, что при изменении фазы или амплитуды гармоники в одном из сигналов (например, в результате сжатия) полной компенсации происходить уже не будет и приведёт к искажению исходного сигнала. Далее это будет показано на конкретных измерениях.
Частичная совместимость
Это свойство явно следует из предыдущего. Так как часть сигнала хранится без сжатия, её можно воспроизвести, игнорируя закодированную часть. Автор преподносит это как достоинство, но оно выглядит крайне сомнительным. Если вы скачали аудио-файл, который не воспроизводится плеером — понятно, что не хватает какого-то кодека. Но если файл воспроизводится с ухудшенным качеством — то логичнее предположить, что так и должно быть или он повреждён, чем искать кодек, улучшающий его звучание.
Разгон
Этим словом автор назвал возможность передискретизации (ресемплиннг, resampling) на уровне декодера. Это можно было бы назвать достоинством, если бы оно приводило к каким-либо значимым преимуществам перед использованием других ресемплеров, в том числе и встроенных в программные аудио-плееры или устройства вывода звука.
Качество ресемплера определяется степенью подавления паразитных гармоник за пределами оригинальной полосы частот. Далее будет показано, что данный кодек таким качеством не обладает.
Расширение динамического диапазона
А здесь уже происходит явная подтасовка фактов. При оцифровке аудио-сигнала происходит не просто уменьшение динамического диапазона — появляются шумы квантования, которые имеют нелинейный характер. Их довольно-таки сложно отфильтровать, поэтому на практике они просто маскируются техниками dithering и noise shaping.
Никакими способами невозможно возместить потерянную информацию, чтобы обеспечив заявленное расширение динамического диапазона. То, что новые выборки звукового потока будут синтезированы в расширенном диапазоне означает лишь отсутствие появление новых шумов квантования — и то лишь на этапе обработки, поскольку устройство воспроизведения звука также имеет ограниченную точность. И к тому же, этим свойством обладают абсолютно все ресемплеры.
Недетерминированное декодирование
Исходя из описания можно было бы предположить, что каждый раз после декодирования мы получаем немного разный результат. Однако реальное сравнение показало, что результаты идентичны. Это значит, что по факту это свойство не имеет никакого значения — с тем же успехом можно увидеть недетерминированность в том, в каком порядке складывать цифры 2 и 3 для получения цифры 5.Испытание на тестовых данных
В статье есть изображение Лены, но нет ни одной осциллограммы. Восполним этот пробел в контексте рассмотрения вносимых кодеком искажений.
Для измерения будут использоваться синтезированные сигналы длительностью 65536 семплов (для удобства последующего Фурье-анализа). Результаты измерений будут представлены как во временной (зелёным цветом), так и в частотной (синим цветом) области в виде логарифмической амплитудно-частотной характеристики.
Изменение амплитуды на 6 дБ примерно равно изменению в 2 раза.
Изменение амплитуды на 12 дБ примерно равно изменению в 4 раза.
При кодировании использовались следующие параметры:
- Maximum sample length of rang = от 4 до 32, для каждого производилось отдельное измерение;
- Length of encoding superframe = 8 (при использовании значения по-умолчанию, 10, файл обрабатывался не полностью и обрезался по правой границе);
- Relative shifting between domains = 1 (по-умолчанию).
MLS — Maximum Length Sequence
Это стандартный инструмент для проведения подобного рода измерений. По виду и на слух он похож на белый шум с той лишь разницей, что ограничен на заданном промежутке времени и имеет дискретный характер. Для аудио-измерений обычно формируется через обратное преобразование Фурье, в котором все амплитуды приравниваются константе, а фазы — псевдослучайным значениям.
После измерения по виду АЧХ можно оценить отклик системы на каждой отдельно взятой частоте по отклонению её амплитуды от 0 дБ.
Поскольку анализировать шум на искажения во временной области довольно проблематично, здесь будут представлены результаты измерений только в частотной области.
Исходный сигнал:
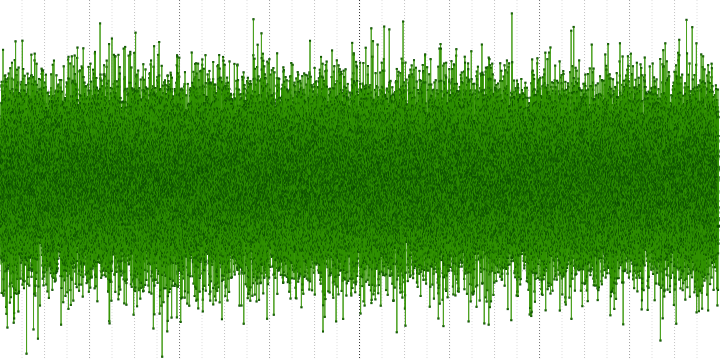
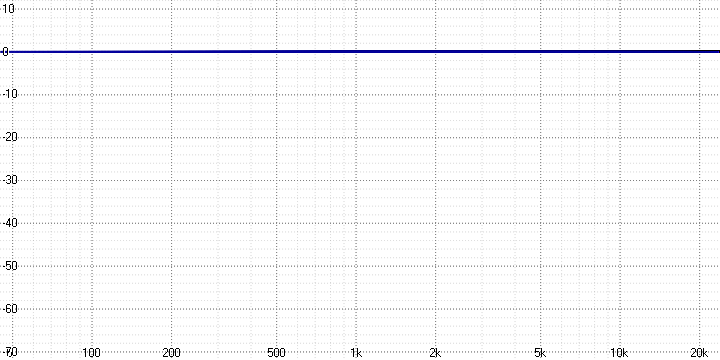
Результаты измерений:
sample length = 4:
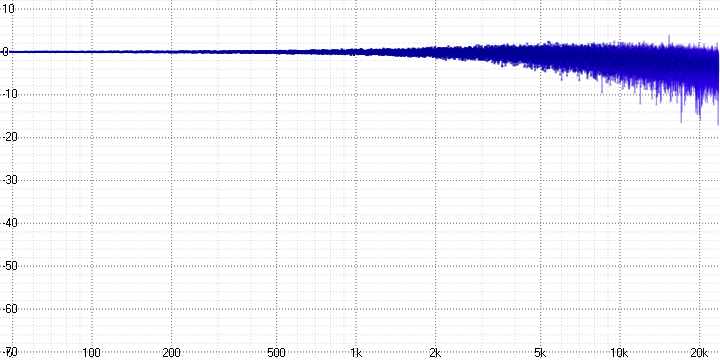
sample length = 8:
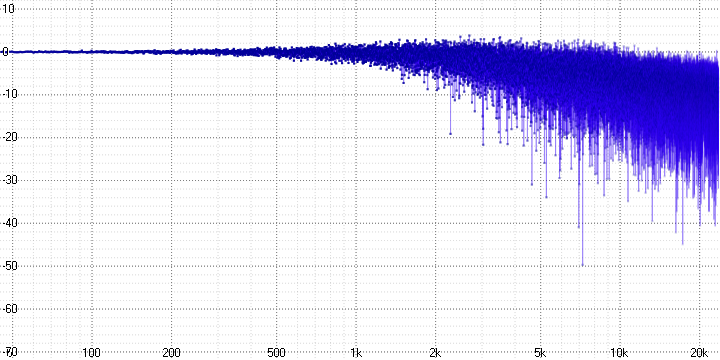
sample length = 16:
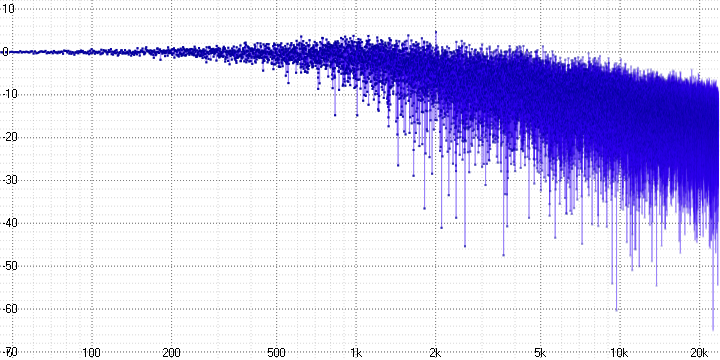
sample length = 32:
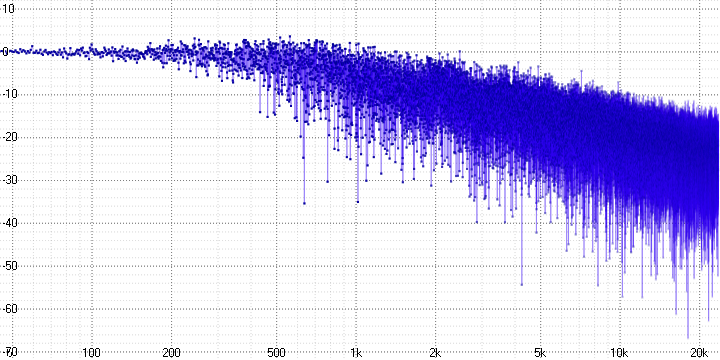
Здесь хорошо виден спад и сильное зашумление на высоких частотах, возрастающих с увеличением параметра sample length (который, вероятно, определяет количество усредняемых точек).
Логарифмический свип-тон (sweep-tone)
Представляет из себя синусоиду с постоянно увеличивающейся или уменьшающейся частотой.
Здесь с уменьшением частоты амплитуда уменьшается, чтобы компенсировать наклон АЧХ (в линейном свип-тоне это не требуется), а также наложено сглаживающее окно.
Его часто используют, чтобы помимо частотного отклика оценить ещё и нелинейные искажения (distortion). Здесь мы никаких коэффициентов считать не будем, а просто оценим результат визуально.
Исходный сигнал:

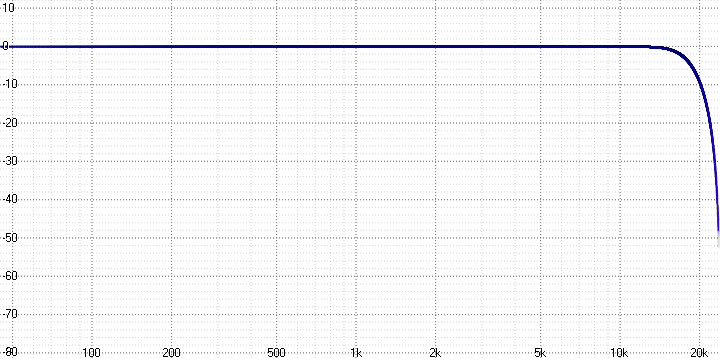
Результаты измерений:
sample length = 4:

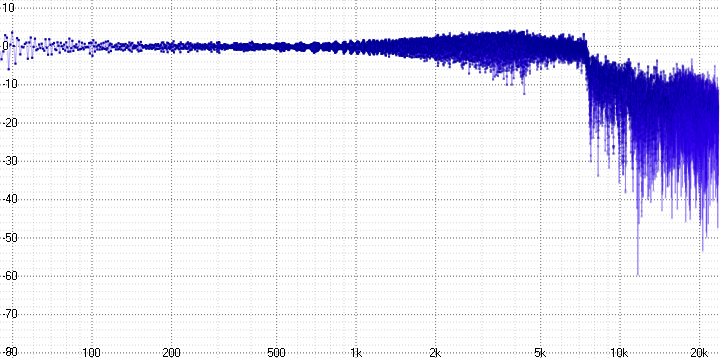
sample length = 8:
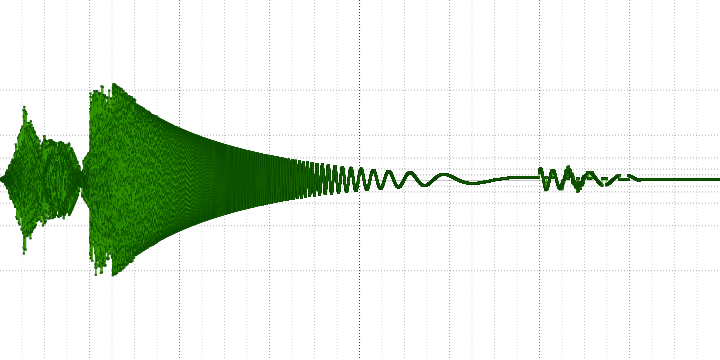
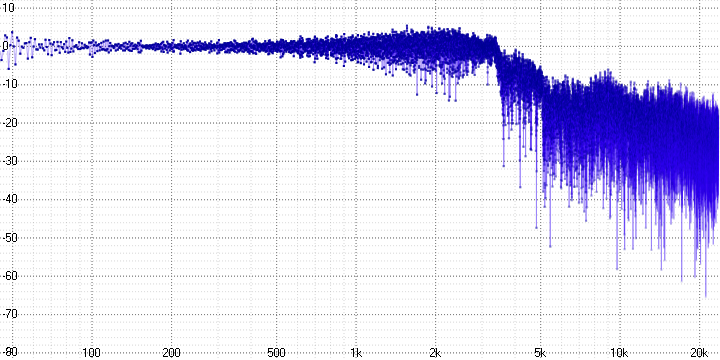
sample length = 16:
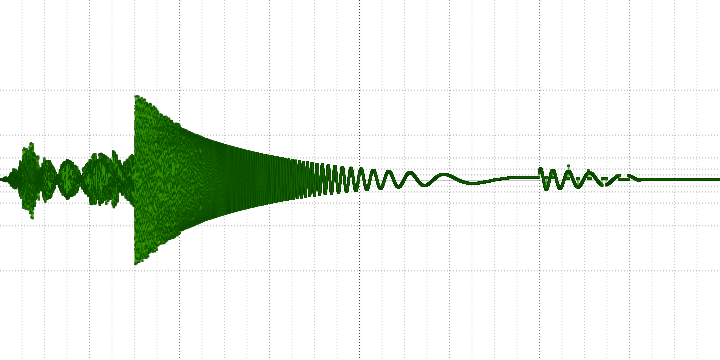

sample length = 32:

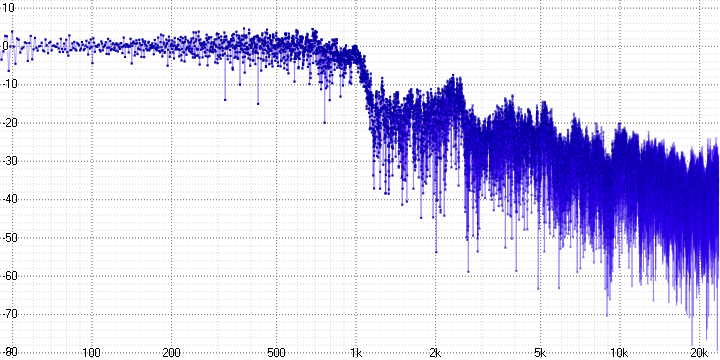
На осциллограмме хорошо видно, что часть высокочастотной информации теряется, и чем больше коэффициент сжатия, тем сильнее.
На АЧХ в то же время видно, что она не просто теряется –, а замещается гармониками (которые неизбежно возникают при децимации усреднением) и шумом.
На осциллограмме также можно увидеть искажение противоположного характера — появления звука там, где его не было. Сложно сказать, является ли это ошибкой или же особенностью алгоритма.
Последовательность из 8 тонов
Содержит ноты «ля» от контроктавы (55 Гц) до «ля» пятой октавы (7040 Гц).
Исходный сигнал:

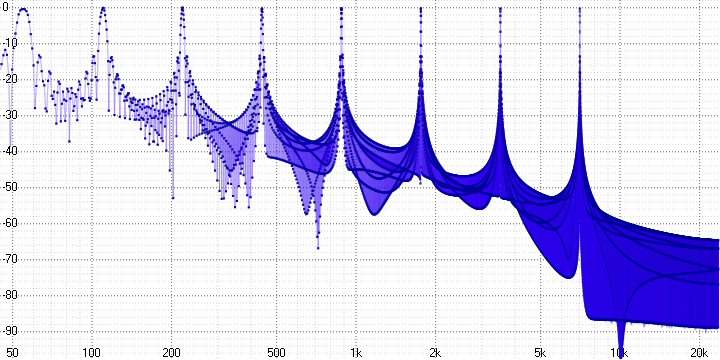
Результаты измерений:
sample length = 4:

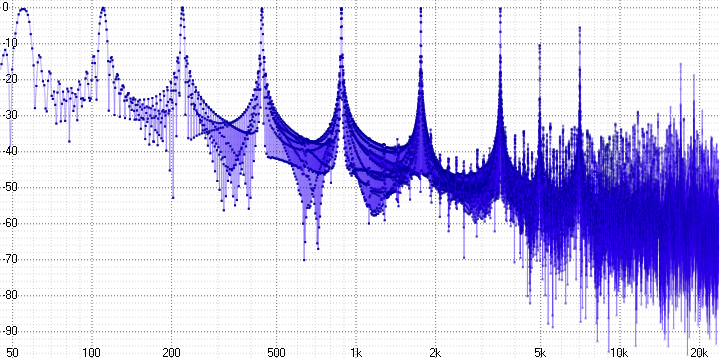
sample length = 8:

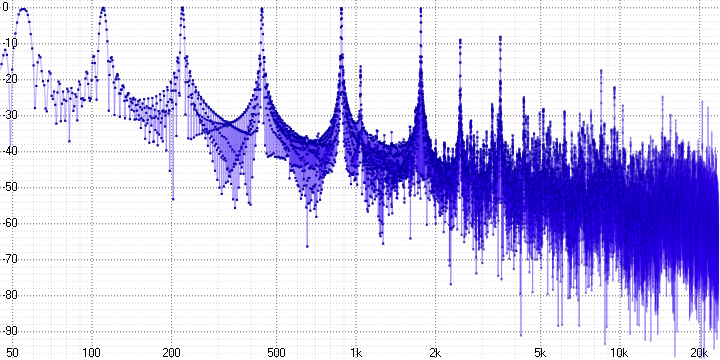
sample length = 16:

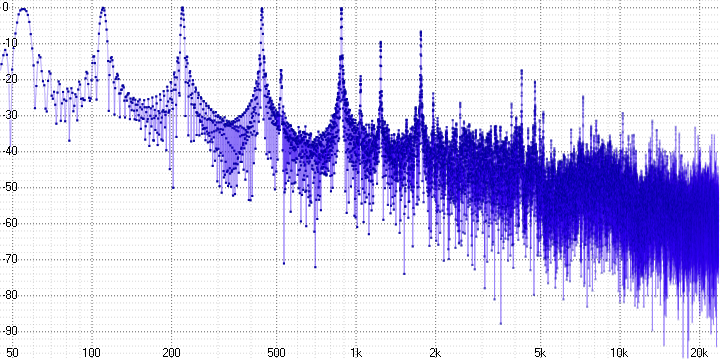
sample length = 32:
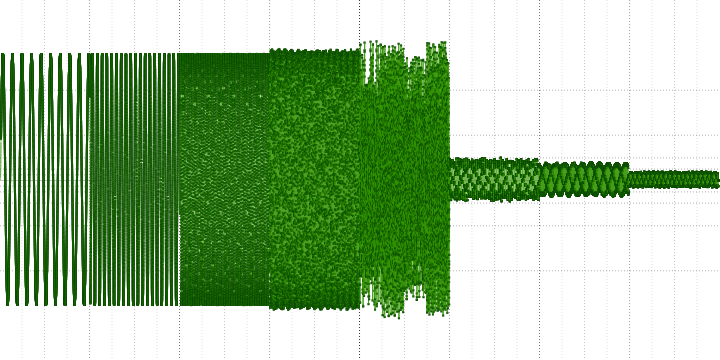
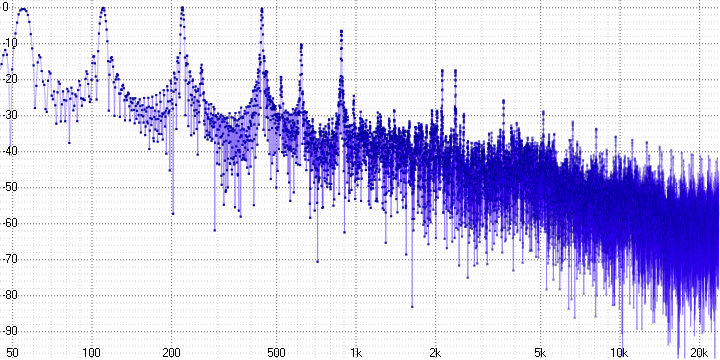
Здесь мы уже можем однозначно утверждать о наличии выраженных гармонических искажений. Поскольку синусоида — это чистый тон, любое её искажение приводит к появлению гармоник — их хорошо видно (на частоте 5 кГц в первом графике, например).
Рассмотрим синусоиду с частотой 440 Гц из последнего замера чуть ближе:
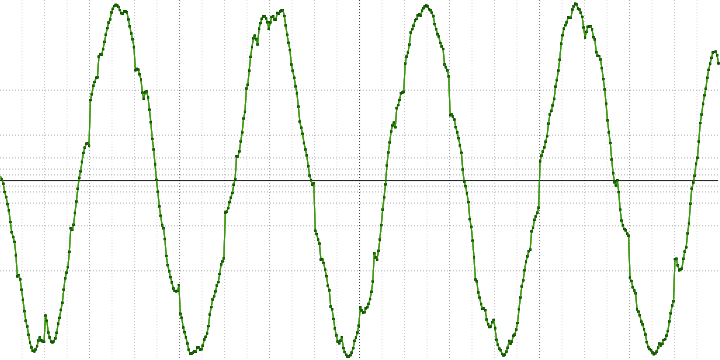
Здесь можно увидеть, что она собрана из кусочков от других синусоид. Также хорошо видно и разрывы на краях блоков.
Испытание «разгона» и расширения динамического диапазона
В декодере есть возможность увеличить частоту дискретизации в 2 или 4 раза и глубину квантования до 24 бит. Испытаем эту возможность на предыдущем сигнале (с параметром sample length = 4):


По форме сигнала видно, что он претерпел ещё бо́льшие искажения. По АЧХ видно, что расширенный частотный диапазон заполнен шумом. Ничего похожего на расширение динамического диапазона также не наблюдается (например, в виде снижения уровня шума).
ЗаключениеРазумеется, из приведённых выше графиков вовсе не следует, что этот кодек нельзя использовать на практике. Вполне возможно, что для кого-то слова «Фрактальное Сжатие» и «Теория Хаоса» будут иметь намного бо́льший вес, чем какие-то там графики. Не менее возможно, что кто-то воспримет его искажения как особенные и приятные на слух, которые только улучшают звучание.
Но лично мне идея фрактального сжатия как таковой кажется притянутой за уши ещё с начала её появления и представляется своего рода «Святым Граалем». Ведь со времени выхода «Фрактальной геометрии природы» ничего особо нового так и не появилось — из книги в книгу кочуют одни и те же фрактальные листья и деревья, множества Мальдеброта и Жулиа, кривые Коха, Гильберта, Пеано и треугольники Серпинского (и оригинальная статья также не стала в этом плане исключением). К тому же, все они имеют исключительно геометрическую природу — никто ещё не заявил о существовании «аудио-фракталов», наделённых свойствами самоподобных множеств с дробной метрической размерностью.
Комментарии (1)
24 сентября 2016 в 15:07
0↑
↓
Спасибо за статью!Но лично мне идея фрактального сжатия как таковой кажется притянутой за уши ещё с начала её появления и представляется своего рода «Святым Граалем». Ведь со времени выхода «Фрактальной геометрии природы» ничего особо нового так и не появилось
Дело не в картинках и геометрии. Дело в том, что не все «хаосы» фрактальны. Фрактальным он становится когда на систему действуют в течении (продолжительного) времени однородные силы (например для биржевых котировок теория хаоса очень хорошо работает). «Полезный» сигнал в аудиозаписи этому условию уже при первом приближении не удовлетворяет. Система конечно, динамическая и всё такое, но не фрактальная, потому что даже вряд ли хаос. Сжатие с потерями всегда достигается (спектральное через Фурье или еще какое другое) при наличии предположений о полезной информации, что противоречит подходу к хаотичным системам.
