Талант против удачи: моделируем успех
В компьютерном моделировании, численных экспериментах, есть ощутимая, но трудновыразимая прелесть. Дело даже не в том, что с помощью простейшей — буквально в десятки строк! — программы удаётся описать и «прокручивать» взад и вперёд сложные процессы из настоящей жизни. Дело скорее в том, что результат работы таких моделей даёт нетривиальные выводы с далеко идущими последствиями.
Вспомните, как мы программировали жизнь по генератору случайных чисел: принимать важные решения, следуя монетке, игровому кубику или, что то же самое, «знакам судьбы», оказывается, не только можно, но часто нужно — важно лишь правильно ограничить риски. Или как наглядно иллюстрировали возможность самостоятельного усложнения вычислительных машин до степени, превосходящей человеческие возможности понимания («Слишком сложные»), с неизбежным превращением человека в беззащитное перед искусственным интеллектом существо («Суперинтеллект и проблема останова»). Как на детском диалекте бейсика решали вполне жизненную задачу, ради доказательства, что пора переходить от тупого перебора вариантов к искусственной интуиции («Как компьютер расправился с покером»).
Сегодня есть возможность продолжить эту серию рассказом о новом интересном эксперименте. Группа исследователей из Италии (A.Pluchino et al), применив всё тот же метод моделирования элементарными цифровыми средствами, смогла выразить численно феномен, давно известный, но до сих пор остававшийся так сказать выведенным на кончике пера. То есть больше ощущаемым, нежели измеренным. Речь о роли случайности или, иначе, удачи в успехе.
Едва ли кто-то возьмётся спорить, что современное общество считает успех результатом почти исключительно личных качеств. Талант и интеллект, навыки и приложенные усилия, трудоспособность и готовность принимать риски — вот ключевые слагаемые успеха. Считается, сделайте на них акцент, используйте по максимуму — и однажды успех обязательно вас настигнет. Настигнет, естественно, в материально-денежном выражении, с чем, полагаю, тоже никто спорить не станет: успешные люди могут быть счастливы или нет, но они уж точно обеспечены! А проблема, давно подмеченная, в частности, философами, но в общем легко обнаруживаемая статистически, в том, что фактические данные этого не подтверждают.
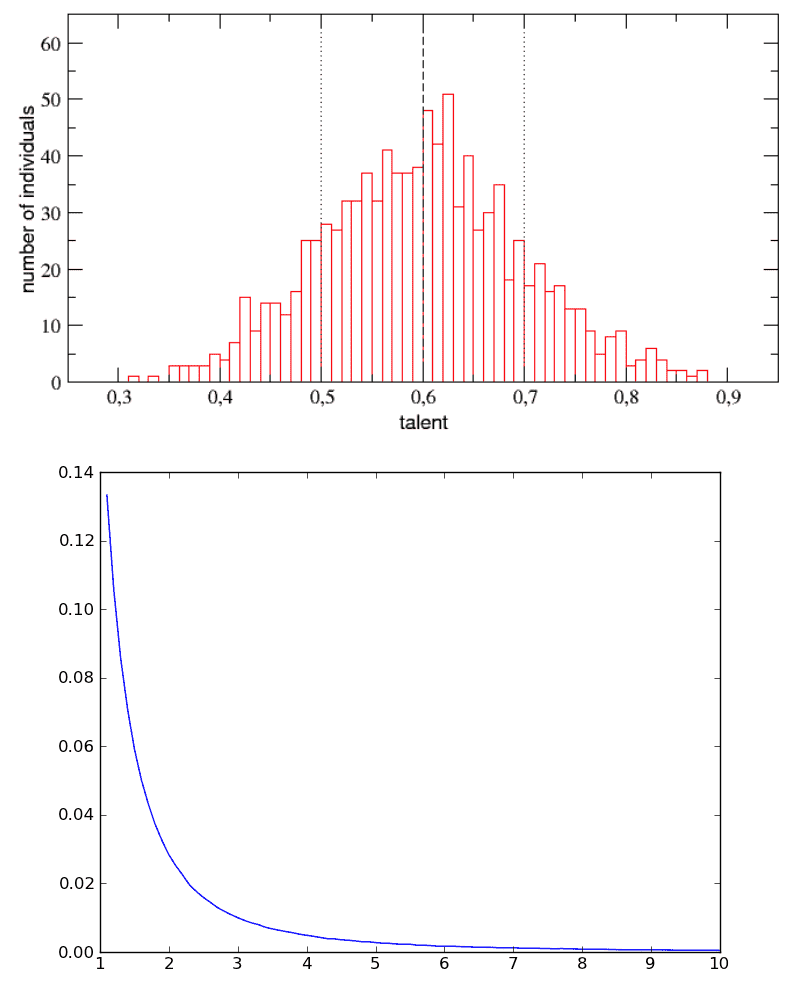Распределение талантливых людей (верхний график; коэффициент интеллекта по горизонтали) против распределения людей успешных (нижний график; личный капитал по вертикали).
Сравните графики распределения людей талантливых и людей успешных. Первый соответствует так называемому нормальному распределению (известно также как гауссово): настоящих талантов и по-настоящему тупых сравнительно немного, они по краям, а между ними масса середнячков. Второй график напоминает закон Парето (резкий всплеск с длинным хвостом): действительно обеспеченных (читайте: успешных!) единицы, остальные — тот самый длинный хвост — живут, что называется, от зарплаты до зарплаты.
Итак, графики очевидно и принципиально отличаются. Но как же так? Ведь если успех действительно есть производная только личных качеств, кривые должны быть идентичны! Ответ, конечно, давно дан, но, повторюсь, выведен он на кончике пера: причина — в удаче, шансе, случайности, везении. Называйте её как угодно, суть не изменится: успех в значительной, если не в большей, степени зависит именно от удачи. Не повезло в жизни — и никакой талант, никакая настойчивость не помогут разбогатеть!
Над этим наблюдением часто подтрунивают: мол, успех всего лишь результат везения, спросите любого неудачника! Но перед статистикой шутники пасуют. Например, проанализируйте профессиональную успешность людей в зависимости от их имён. В идеальном мире, где успех есть только производная таланта (назовём так совокупный набор личных качеств), зависимости между именем человека и его успехами на службе/работе быть, естественно, не может и не должно (если интересны подробности, вспомните, что естественные числовые ряды следуют так называемому закону Бенфорда и это позволяет, например, вскрывать мошенничества). В действительности же статистика обнаруживает множество отклонений от идеала.
Так люди, подписывающиеся с употребление отчества, чаще упоминаются как одарённые. А учёные с именами, начинающимися ближе к началу алфавита, чаще продвигаются по службе. Равно и в начальники вообще чаще пробиваются люди с гордо звучащими именами. И так далее, и так далее — не стану утомлять вас ссылками на оригиналы научных работ, все они есть в исследовании, о которой сегодня пойдёт речь.
Иначе говоря, несомненно, что таланта для успеха недостаточно, нужна ещё удача. Извечный вопрос: в какой пропорции две этих компоненты должны быть смешаны? Тут мы и приходим к работе, выполненной итальянцами. Построив простую программную модель общества, они смогли измерить влияние удачи и, что даже более важно, сделать из этого практически полезные выводы.
В качестве среды они выбрали не просто язык программирования, а уже готовый инструмент для моделирования сообществ: NetLogo. Это свободный продукт (развивается под лицензией GPL), исходники самой модели авторы также опубликовали, поэтому при желании весь эксперимент легко повторить на собственном столе.
Суть: на ограниченном пространстве размещается тысяча человек. Каждый из них наделён одинаковым капиталом и различной случайной степенью таланта (то есть, повторюсь, суммой личных качеств: интеллект, навыки, трудоспособность и прочее), причём распределение повторяет наблюдаемое в реальности (гауссово).
По этому же пространству случайно разбрасывается тысяча точек, половина из которых символизируют «удачную возможность» (зелёные), другая половина — «невезение» (красные). Точки движутся по случайным траекториям, а вся симуляция идёт шестимесячными отрезками на протяжении 40 лет. Важно, что столкновение индивида с «невезением» сокращает его капитал вдвое, а вот столкновение с «удачей» капитал удваивает, но не всегда, а с вероятностью, пропорциональной таланту. То есть чем более одарён индивид, тем выше вероятность, что он предоставившимся шансом воспользуется.
Как видите, модель местами весьма упрощена (в частности, в отношении к риску: убытки важно ограничивать — и это давно не секрет), но всё же основные её свойства повторяют наблюдаемое в настоящем обществе: талантливых людей сравнительно немного и они имеют большие шансы воспользоваться выпавшей удачей. Оказываются идентичны реальности и результаты прогона этой модели (как однократного, так и многократных): мы получаем типичное парето-распределение, в котором огромное число неудачников противостоит буквально единицам, добившимся успеха (единицы миллиардёров против миллиардов, живущих на зарплату: знакомо?).
Многократный прогон несколько смещает центр тяжести в сторону более талантливых людей, однако принципиально картина остаётся той же: удача играет в судьбах наших виртуальных героев первую скрипку!
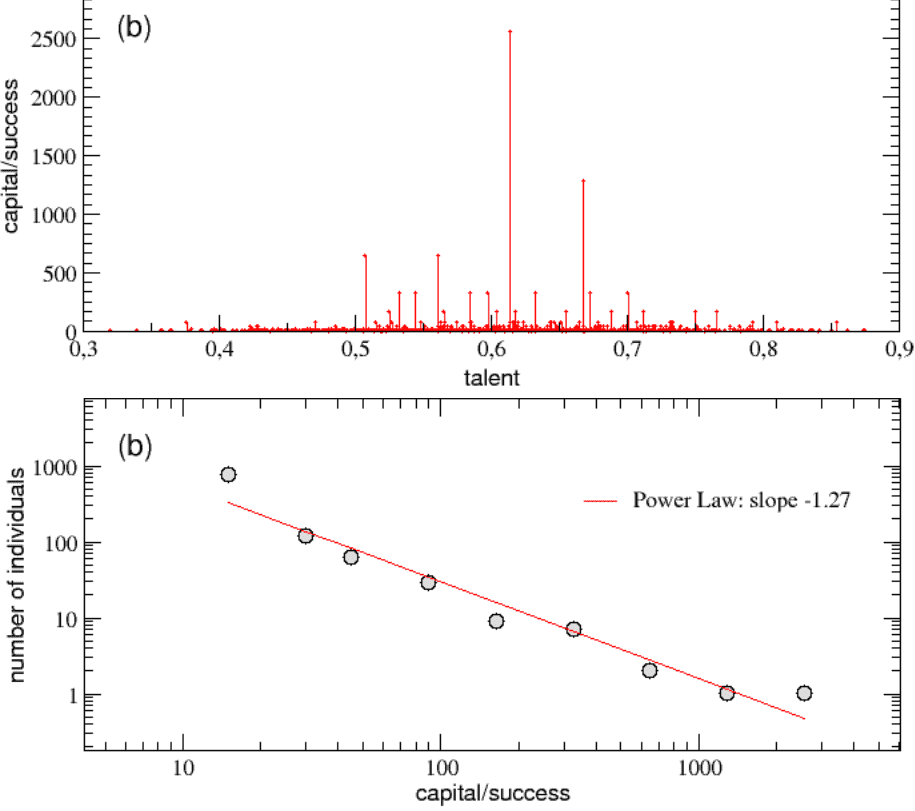Результаты моделирования. Как видите, успеха добились главным образом индивиды с талантом около среднестатистического (верхний график). И успешных людей очень, очень немного по сравнению со всеми остальными (нижний график: обратите внимание, он логарифмический, то есть каждое деление по вертикали отличается от предыдущего в 10 раз).
Переводя с языка цифр, мы видим, что наибольший шанс пробиться к «вершине успеха» имеют счастливчики-середнячки — просто потому, что их больше и им, суммарно, чаще везёт. Тогда как люди талантливые вероятностно обречены прозябать в бедности и безвестности. И это позволяет сделать два важных вывода.
Во-первых, даже если вы объективно одарённый человек, полагаться только на одарённость не следует. Одного таланта для успеха недостаточно!
Во-вторых, методика стимулирования талантливых людей (и проектов, что в социальном контексте то же самое), принятая в современном обществе, объективно плоха! Успешность принимается за меру таланта — и её вознаграждают, стимулируют. Но выходит так, что вознаграждаются в основном люди, добившиеся успеха благодаря чистому везению. И это ещё более усиливает негативный эффект как для личности, так и для общества: ведь стимулирующие фонды не бездонны — и в результате настоящие таланты страдают от нехватки возможностей. Авторы работы называют это наивной меритократией.
Но что же делать? Как исправить эту несправедливость, уравновесить влияние слепого везения? К счастью, в наших руках модель, а значит, возможно проверить влияние любых стратегий на финальное распределение. Опуская здесь все проверенные варианты (отсылаю к оригиналу — который читается легко и даже увлекательно, если только вы немного знакомы с программированием и математикой), назову лишь показавшие наилучший результат.
На индивидуальном уровне важно предоставить себя как можно более широкому потоку случайностей. Работайте над большим количеством идей, диверсифицируйте темы, области знаний и деятельности, в которых вы заняты, расширьте круг общения. В результате вы поймаете больше удачных моментов, которыми, как человек предположительно талантливый, сможете воспользоваться лучше «середнячков», выезжающих на чистой удаче.
На уровне же социальном наиболее эффективной оказывается стратегия равных возможностей. Иначе говоря необходимо прекратить поощрять только людей, добившихся успеха. Это порочная практика, усиливающая влияние удачи: возможности не бесконечны, а значит, отдав их «везунчикам», мы обделим многих по-настоящему одарённых (но менее везучих) индивидов. Поэтому важно распределить возможности равномерно, без приоритетов: если речь о науке — гранты, если речь об образовании — доступ к знаниям, если речь об обществе в целом — стимулы в широком понимании. Только тогда модель показывает наивысший процент талантливых людей, среди добившихся успеха.
Правда, не обольщайтесь: даже тогда, среди пробившихся на вершину успеха, талантливых лишь около двух третей
Полный текст статьи читайте на Компьютерра
