Рассуждение о природе «замороженной случайности» в распределении простых чисел18.04.2024 12:30

Гипотеза о природе сложности

Недавно в ленте FB попалось интереснейшее видео Теория Всего и феноменологическая Теория Сложности. Что это и почему это важно? где, помимо всего прочего интересного, прозвучала следующая цитата:

Идея самоиндуцированных спиновых стекол состоит в том, что беспорядок, в общем-то, не нужен, а что нужно нужно то, что называется фрустрации, или то, что называется конкурирующее взаимодействие. То есть когда у вас на систему действует несколько разнонаправленных тенденций и каждая хочет систему упорядочить, но каждая хочет систему упорядочить по-своему. Когда они все присутствуют одновременно и действуют одновременно система не может выбрать куда ей упорядочиваться. И вот она приходит в это в это состояние спинового стекла, несмотря на то что никакого беспорядка нет.

Михаил Кацнельсон, ©

(Примечание: Спиновые стёкла рассматриваются как состояние магнитной системы со случайным распределением спин-спиновых взаимодействий. В системе отсутствует дальний порядок, причем беспорядок в системе замороженный, то есть не меняется со временем).

Я достаточно далёк от физики в целом и данной тематики в частности, но вот сам тезис о связи конкурирующих взаимодействий и свойствах сложных систем демонстрировать, с одной стороны квази-случайное поведение, а с другой определённые закономерности показался очень любопытным, поскольку вызвал ассоциации с совершенно неожиданным объектом для сравнения — простыми числами. Точнее с их распределением.

В этой связи приведу другой тезис, кторый буду использовать как вторую отправную точку:

Ни нули дзета-функции Римана, ни собственные значения гауссовой случайной эрмитовой матрицы не похожи на случайно разбросанные точки (отличаются от идеально случайного разброса);

С одной стороны, рапределение простых чисел выглядит вполне случайным (хотя, право, мало ли что как выглядит…?!!), с другой стороны — случайность тут тоже «замороженная», ну, а с третьей — присутствуют и закономерности.

В частности, имеется:

Теорема о распределении простых чисел

С неё и начнем.

Функция a (x)

Рассмотрим некоторую функцию a(x) где $x \in \mathbb{R}$ , x > 0» src=«https://habrastorage.org/getpro/habr/upload_files/1e3/eda/b68/1e3edab6845cc116921dd2fc3d356667.svg» /> такую что точно выполняется соотношение: 

<img alt=

Из (1) выразим a(x) :

$x = \pi(x) \cdot \log_{a(x)}{x}$ $\log_{a(x)}{x} = \frac{x}{ \pi(x) }$ $a(x)^{\frac{x}{\pi(x)}} = x$ $(a(x)^{\frac{x}{\pi(x)}})^{\frac{\pi(x)}{x}} = x^{\frac{\pi(x)}{x}}$

Получим a(x) :

$a(x) = x^{\frac{\pi(x)}{x}} \text{ (2)}$

Мы определели такую функцию a(x) , значения которой есть основания логарифма числа при котором соотношение (1) в точности соответсвует распределению простых чисел (т.е. функции $\pi(x)$ ).

(Рис. 1) Функция при небольших

(Рис. 1) Функция a(x)

при небольших

(Рис. 2) Функция при достаточно больших

(Рис. 2) Функция a(x)

при достаточно больших

Можно заметить, что характерный ступенчатый вид функции естественным образом обусловлен свойствами базовых функций $\pi(x)$ и $a_{k}(x)$ .

(Рис. 3) Функция распределения простых чисел до значения

(Рис. 3) Функция распределения простых чисел $\pi(x)$ до значения x = 200

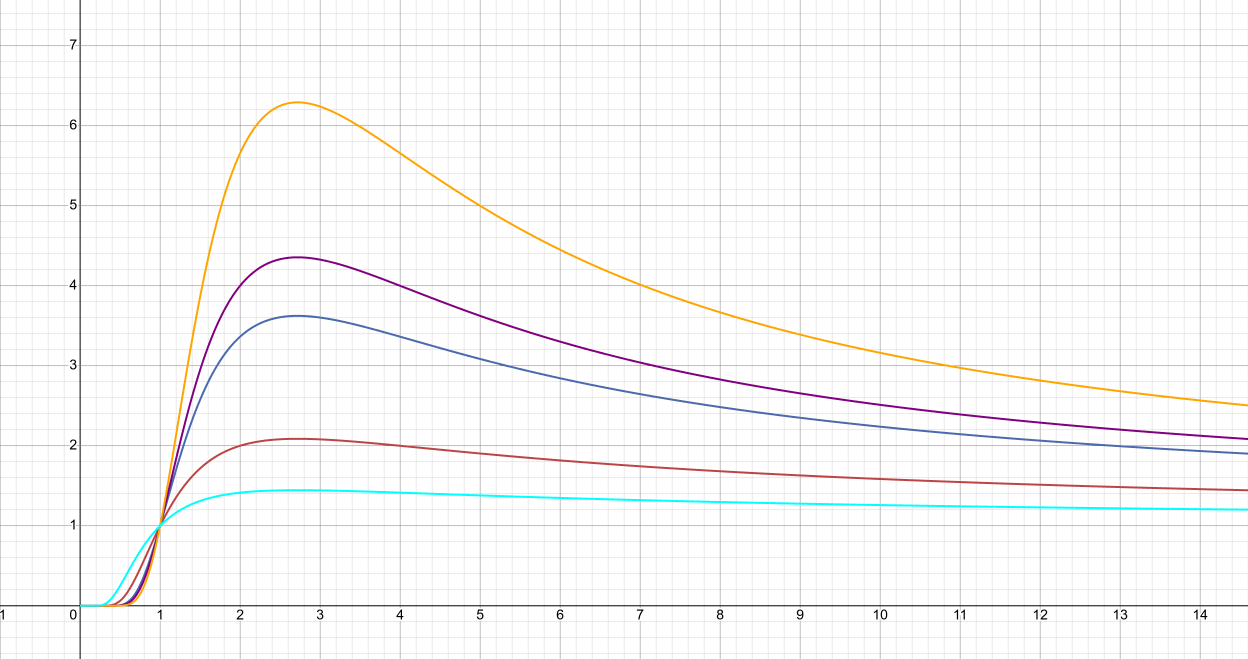
(Рис. 4) Семейство функций вида .

(Рис. 4) Семейство функций вида $a_{k}(x) = x^{\frac{k}{x}}$ $k \in \mathbb{N}$ .

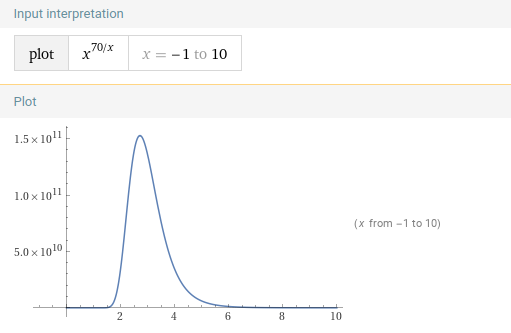
(Рис. 5) Функция

Посмотрим на функции внимательней.

Элементарные свойства функций a_k (x) и π (x)

Семейство функций вида $a_{k}(x) = x^{\frac{k}{x}}$ $k \in \mathbb{N}$ для $\forall k \in \mathbb{N}$ и $\forall x \in \mathbb{R}$ x > 0» src=«https://habrastorage.org/getpro/habr/upload_files/cd3/412/ebc/cd3412ebc6a55c0f2cd43eddab1cde39.svg» /> имеет ряд примечательных свойств: 

1.1. <img alt= имеет единственный максимум при x = e равный $e^{\frac{k}{e}}$ и монотонно и достаточно быстро убывает для всех $x \gg e$ .
1.2. $\lim_{x\to +\infty}{a_{k}(x)} \to 1$
1.3. $\forall x>1» src=«https://habrastorage.org/getpro/habr/upload_files/752/acc/fe0/752accfe0f8939883ee4deb3c18a9a77.svg» /><img alt=$ a_{k}(x)» src=«https://habrastorage.org/getpro/habr/upload_files/5fc/f3b/c70/5fcf3bc70b2ed15a33867b7640fd6f26.svg» />
1.4. $a_{k}(x)$ растёт крайне быстро и до очень больших значений на фиксированном интевале (0;e] .

Функция $\pi(x)$ обладает следующими элементарными свойствами:
2.1. $0 < \pi(x) < x$
2.2 $0 \leq \pi(x_{i+1}) - \pi(x_{i}) \leq 1$ неубывающая ступенчатая функция.

Интерпретация графика a (x)

Несложно заметить, что функция a(x) (Рис. 1) является композицией функций $a_{k}(x)$ (Рис. 4), на интервалах $[p_0,p_1), [p_1,p_2), ...,[p_i,p_{i+1}), [p_{i+1},p_{i+2}), ...$ по всем простым p_i , где $k=\pi(x)$ для $x \in [p_i, p_{i+1}-1)$ .

Поскольку на каждом интервале значение $\pi(x)=const$ , то каждому интервалу соответсвует свой ниспадающий участок соответсвующей функции $a_{k}(x)$ (»гирлянда»).

В силу 1.3 $a_{k+1}(x) > a_{k}(x)» src=«https://habrastorage.org/getpro/habr/upload_files/86d/26f/12c/86d26f12c9f0ec38c9861f4dc7ded07e.svg» /> каждое появление нового простого числа (в силу 2.2) гарантированно поднимает график вверх (»вершина гирлянды — простое число») выше предыдущего значения, а каждое последующее <img alt=$ e» src=«https://habrastorage.org/getpro/habr/upload_files/e94/052/162/e94052162ccc0d5694353d1219a6a3bf.svg» /> в силу 1.1 снова опускает его.

В силу того, что множество простых чисел бесконечно, а в силу 1.1 функция убывает и в то же время в силу 1.2 не опускается ниже 1 мы имеем постоянно действующий процесс взаимно конкурирующих взаимодействий.

Вывод

Согласно базовой гипотезе, наличие этих «фрустраций» (в смысле данном выше), вероятно, и может определять «случайный» характер распределения простых чисел.

P.S. Предел a (x)

Глядя на Рис. 2 можно предположить, что:

$\lim_{x\to +\infty}{a(x)} \to e$

Во всяком случае, это было бы красиво :)

Habrahabr.ru прочитано 3096 раз