[Перевод] Алгоритмы обнаружения контуров изображения
В статье представлены четыре самых распространённых алгоритма обнаружения контуров.
Первые два, а именно алгоритм трассировки квадратов и трассировка окрестностей Мура, просты в реализации, а потому часто применяются для определения контура заданного паттерна. К сожалению, у обоих алгоритмов есть несколько слабых мест, что приводит к невозможности обнаружения контура большого класса паттернов из-за их особого вида смежности.
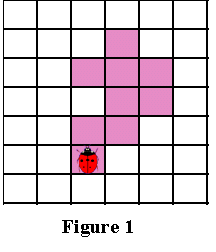
Данные алгоритмы будут игнорировать все «дырки» в паттерне. Например, если у нас есть паттерн, подобный показанному на Рисунке 1, то обнаруженный алгоритмами контур будет похож на показанный на Рисунке 2 (синими пикселями обозначен контур). В некоторых областях применения это вполне допустимо, но в других областях, например, в распознавании символов, требуется обнаружение внутренних частей паттерна для нахождения всех пробелов, отличающих конкретный символ. (На Рисунке 3 показан «полный» контур паттерна.)

Следовательно, для получения полного контура сначала необходимо использовать алгоритм «поиска дырок», определяющий отверстия в заданном паттерне, а затем применить к каждому отверстию алгоритм обнаружения контуров.

Что такое связность
В цифровых изображениях с двоичными значениями пиксель может иметь одно из следующих значений: 1 — когда является частью паттерна, или 0 — когда является частью фона, т.е. градации серого отсутствуют. (Мы будем считать, что пиксели со значением 1 чёрные, а со значением 0 — белые).
Для идентификации объектов в цифровом паттерне нам нужно находить группы чёрных пикселей, «связанных» друг с другом. Другими словами, объектами в заданном цифровом паттерне являются связные компоненты этого паттерна.
В общем случае, связная компонента — это множество чёрных пикселей P, такое, что для каждой пары пикселей pi и pj в P существует последовательность пикселей pi, …, pj, такая, что:
a) все пиксели в последовательности находятся во множестве P, т.е. являются чёрными, и
b) каждые 2 пикселя, находящиеся в последовательности рядом, являются «соседями».
Возникает важный вопрос: когда мы можем сказать, что 2 пикселя являются «соседями»? Поскольку мы используем квадратные пиксели, ответ на предыдущий вопрос нетривиален по следующей причине: в квадратной тесселяции пиксели имеют общее или ребро, или вершину, или не имеют ничего общего. У каждого пикселя есть 8 пикселей, имеющих с ним общую вершину; такие пиксели составляют «окрестность Мура» данного пикселя. Должны ли мы считать «соседями» пиксели, имеющие только одну общую вершину? Или чтобы считаться «соседями», два пикселя должны иметь общее ребро?
Так возникают два вида связности, а именно: 4-связность и 8-связность.
4-связность
Когда мы можем сказать, что заданное множество чёрных пикселей является 4-связным? Во-первых, нужно определить понятие 4-соседа (также называемого прямым соседом):
Определение 4-соседа: пиксель Q является 4-соседом заданного пикселя P, если Q и P имеют общее ребро. 4-соседи пикселя P (обозначенные как P2, P4, P6 и P8), показаны на Рисунке 2 ниже.

Определение 4-связной компоненты: множество чёрных пикселей P является 4-связной компонентой, если для каждой пары пикселей pi и pj в P существует последовательность пикселей pi, …, pj, такая, что:
a) все пиксели в последовательности находятся во множестве P, т.е. являются чёрными, и
b) каждые два пикселя, которые находятся рядом в последовательности, являются 4-соседями
Примеры 4-связных паттернов
На схемах ниже показаны примеры 4-связных паттернов:

8-связность
Когда можно сказать, что заданное множество чёрных пикселей 8-связное? Во-первых, нам нужно определить понятие 8-соседа (также называемого непрямым соседом):
Определение 8-соседа: пиксель Q является 8-соседом (или просто соседом) заданного пикселя P, если Q и P имеют общее ребро или вершину. 8-соседи заданного пикселя P составляют окрестность Мура этого пикселя.
Определение 8-связной компоненты: множество чёрных пикселей P является 8-связной компонентой (или просто связной компонентой), если для каждой пары пикселей pi и pj в P существует последовательность пикселей pi, …, pj, такая, что:
a) все пиксели в последовательности находятся во множестве P, т.е. являются чёрными, и
b) каждые два пикселя, которые находятся рядом в этой последовательности, являются 8-соседями
Примечание: все 4-связные паттерны являются 8-связными, т.е. 4-связные паттерны являются подмножеством множества 8-связных паттернов. С другой стороны, 8-связный паттерн может и не являться 4-связным.
Пример 8-связного паттерна
На схеме ниже показан паттерн, являющийся 8-связным, но не 4-связным:

Пример паттерна, не являющегося 8-связным:
На схеме ниже показан пример паттерна, не являющийся 8-связным, т.е. составленный из более чем одной связной компоненты (на схеме показаны три связные компоненты):

Алгоритм трассировки квадратов
Идея
Лежащая в основе алгоритма трассировки квадратов идея очень проста; это можно связать с тем фактом, что алгоритм стал одной из первых попыток обнаружения контура двоичного паттерна.
Чтобы понять, как он работает, нужно немного воображения…
Допустим, у нас есть цифровой паттерн, например, группа из чёрных пикселей на фоне из белых пикселей, т.е. на сетке; находим чёрный пиксель и объявляем его нашим »начальным» пикселем. (Нахождение »начального» пикселя можно реализовать множеством разных способов; мы начнём с левого нижнего угла сетки, будем сканировать каждый столбец пикселей снизу вверх, от самого левого столбца и до самого правого, пока не натолкнёмся на чёрный пиксель. Его мы и объявим »начальным».)
Теперь представьте, что вы — божья коровка, стоящая на начальном пикселе, как это показано на показанном ниже Рисунке 1. Чтобы получить контур паттерна, вам необходимо сделать следующее:
каждый раз, когда вы оказываетесь на чёрном пикселе, поворачивайте налево, и
каждый раз, когда вы оказываетесь на белом пикселе, поворачивайте вправо,
пока снова не доберётесь до начального пикселя.
Чёрные пиксели, которые вы обошли, будут являться контуром паттерна.
Важным аспектом алгоритма трассировки квадратов является «чувство направления». Повороты влево и вправо выполняются относительно текущего расположения, которое зависит от того, каким образом вы попали на текущий пиксель. Следовательно, чтобы делать правильные ходы, необходимо отслеживать своё направление.
Алгоритм
Ниже представлено формальное описание алгоритма трассировки квадратов:
Входящие данные: квадратная тесселяция, T, содержащая связную компоненту P чёрных ячеек.
Выходные данные: ряд B (b1, b2,…, bk) пикселей границы, т.е. контур.
Начало
Конец
Примечание: понятия «влево» и «вправо» следует рассматривать не относительно страницы или читателя, а относительно направления входа в «текущий» пиксель во время выполнения сканирования.
Демонстрация
Ниже показана анимированная демонстрация того, как алгоритм трассировки квадратов обнаруживает контур паттерна. Не забывайте, что божья коровка движется по пикселям; замечайте, как меняется её направление при поворотах влево и вправо. Повороты влево и вправо выполняются относительно текущего направления в пикселе, т.е. ориентации божьей коровки.

Анализ
Оказывается, что возможности алгоритма трассировки квадратов очень ограничены. Он неспособен обнаруживать контуры большого семейства паттернов, которые часто возникают в реальных областях применения.
В основном это связано с тем, что повороты влево и вправо не учитывают пиксели, расположенные «по
диагонали» от текущего пикселя.
Давайте рассмотрим различные паттерны с разной связностью и увидим, почему терпит неудачу алгоритм трассировки квадратов. Кроме того, мы изучим способы усовершенствования возможностей алгоритма и заставим его работать хотя бы с паттернами, имеющими особый вид связности.
Критерий останова
Одна из слабостей алгоритма заключается в выборе критерия останова. Другими словами, когда алгоритм прекращает своё выполнение?
В исходном описании алгоритма трассировки квадратов условием завершения является попадание в начальный пиксель во второй раз. Оказывается, что если алгоритм зависит от такого критерия, то он не сможет обнаружить контуры большого семейства паттернов.
Ниже показана анимированная демонстрация с объяснением того, как алгоритму не удаётся обнаружить точный контур паттерна из-за выбора плохого критерия останова:

Как видите, усовершенствование критерия останова может стать хорошим началом для улучшения результативности алгоритма в целом. Существует две эффективные альтернативы для имеющегося критерия останова:
a) Останавливаться, только посетив начальный пиксель n раз, где n не меньше 2, ИЛИ
b) Останавливаться после попадания в начальный пиксель во второй раз точно так же, как мы попали в него изначально.
Этот критерий был предложен Джейкобом Элиософфом, поэтому мы будем называть его критерием останова Джейкоба.
Смена критерия останова в общем случае улучшает результативность алгоритма трассировки квадратов, но не позволяет преодолеть другие слабые места, которые он имеет в случае паттернов с особыми видами связности.
Square Tracing Algorithm неспособен обнаружить контур семейства паттернов со связностью 8, которые НЕ имеют связности 4.
Ниже показана анимированная демонстрация того, как алгоритму трассировки квадратов (с критерием останова Джейкоба) не удаётся обнаружить правильный контур паттерна со связностью 8 без связности 4:

Этот алгоритм совершенно бесполезен?
Если вы прочитали представленный выше анализ, то наверно думаете, что алгоритму трассировки квадратов не удаётся обнаружить контуры большинства паттернов. Но оказывается. что существует особое семейство паттернов, у которого полностью правильно обнаруживается контур алгоритмом трассировки квадратов.
Пусть P — множество чёрных пикселей со связностью 4 на сетке. Пусть белые пиксели сетки, т.е. фоновые пиксели W тоже имеют связность 4. Оказывается, что при таких условиях паттерна и его фона можно доказать, что алгоритм трассировки квадратов (с критерием останова Джейкоба) всегда успешно будет справляться с определением контура.
Ниже представлено доказательство, что в случае, когда и паттерн, и пиксели фона имеют связанность 4, алгоритм трассировки квадратов будет правильно определять контур при использовании критерия останова Джейкоба.
Доказательство
Дано: паттерн P такой, что все пиксели паттерна (т.е. чёрные) и пиксели фона (т.е. белые) W имеют связность 4.
Первое наблюдение
Так как множество белых пикселей W имеет связность 4, это значит, что в паттерне не может быть никаких »дыр» (выражаясь неформально,»дырами» мы называем группы белых пикселей, полностью окружённые чёрными пикселями паттерна).
Наличие любой »дыры» в паттерне приведёт к отделению группы белых пикселей от остальных белых пикселей; при этом множество белых пикселей теряет связность 4.
На Рисунке 2 и Рисунке 3 ниже показано два вида »дыр», которые могут возникнуть в паттерне со связностью 4:

Второе наблюдение
Любые два чёрных пикселя паттерна ОБЯЗАНЫ иметь одну общую сторону.
Допустим, два чёрных пикселя имеют только одну общую вершину. Тогда, чтобы удовлетворить свойству 4-связности паттерна, должен существовать путь, соединяющий эти два пикселя так, что каждые два соседних пикселя на этом пути имеют связность 4. Но это даст нам паттерн, похожий на Рисунок 3. Другими словами, это приведёт к разделению белых пикселей. На Рисунке 4 ниже показан типичный паттерн, удовлетворяющий допущению, что пиксели паттерна и фона 4-связаны, т.е. не имеют »дыр», а каждые два чёрных пикселя имеют одну общую сторону:

Полезно представлять такие паттерны следующим образом:
Сначала рассматриваем граничные пиксели, т.е. контур паттерна. Затем если мы рассмотрим каждый граничный пиксель как имеющий 4 ребра единичной длины, то увидим, что некоторые из этих рёбер общие с соседними белыми пикселями. Мы назовём такие рёбра граничными рёбрами.
Такие граничные рёбра можно рассматривать как рёбра многоугольника. На Рисунке
5 ниже эта мысль продемонстрирована на примере многоугольника, соответствующего паттерну с Рисунка 4 выше:

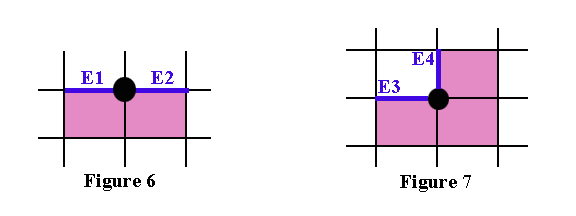
Если мы рассмотрим все возможные «конфигурации» граничных пикселей, которые могут возникать в таких паттернах, то увидим, что существует два простых случая, показанных на Рисунке 6 и Рисунке 7 ниже.
Граничные пиксели могут быть кратными этих случаев или другими расположениями, т.е. поворотами этих двух случаев. Граничные рёбра помечены синим как E1, E2, E3 и E4.
Третье наблюдение
В случае рассмотренных выше двух случаев, какой бы начальный пиксель мы не выбрали, и в каком бы направлении в него не попали, алгоритм трассировки квадратов никогда не будет «возвращаться назад» (backtrack), никогда не будет «проходить через» граничное ребро дважды (только если он не трассирует границу во второй раз) и никогда не пропустит граничное ребро. Проверьте!
Здесь нужно пояснить две концепции:
a) алгоритм «возвращается назад», когда перед трассировкой всей границы он идёт назад, чтобы посетить уже посещённый пиксель, и
b) для каждого граничного ребра существует два способа «пройти через него», а именно «внутрь» и «наружу» (где «внутрь» обозначает движение внутрь соответствующего многоугольника, а «наружу» — наружу многоугольника).
Кроме того, когда алгоритм проходит «внутрь» через одно из граничных рёбер, он пройдёт «наружу» через следующее граничное ребро, т.е. алгоритм трассировки квадратов не должен иметь возможности пройти сквозь два последовательных ребра одинаковым образом.
Последнее наблюдение
У каждого паттерна существует чётное количество граничных рёбер.
Если посмотреть на многоугольник с Рисунка 5, то можно увидеть, что:
если мы хотим начать с вершины S, отмеченной на схеме, и следовать по граничным рёбрам, пока снова не достигнем S, то заметим, что пересечём в процессе чётное количество граничных рёбер. Можно считать каждое граничное ребро «шагом» в отдельном направлении. Тогда для каждого «шага» вправо должен быть соответствующий «шаг» влево, если мы хотим вернуться в исходную позицию. То же самое относится к вертикальным «шагам». Следовательно, «шаги» должны иметь соответствующие пары и это объясняет, почему в каждом из таких паттернов будет чётное количество граничных рёбер.
Следовательно, когда алгоритм трассировки квадратов входит через начальное граничное ребро (начального пикселя) во второй раз, то он будет это делать в том же направлении, что и в первый раз.
Причина этого в том, что поскольку существует два способа прохода через граничное ребро, и алгоритм попеременно выполняет движение «внутрь» и «наружу», а граничных рёбер чётное количество, то алгоритм пройдёт через начальное граничное ребро во второй раз так же, как и в первый.
Заключение
В случае 4-связного паттерна и фона алгоритм трассировки квадратов обнаружит всю границу, т.е. контур, паттерна и прекратит работу после однократной трассировки, т.е. не будет трассировать её заново, поскольку при достижении начального граничного ребра во второй раз он войдёт в него так же, как и в первый раз. Следовательно, алгоритм трассировки квадратов с критерием останова Джейкоба будет правильно определять контру любого паттерна при условии, что и паттерн, и фон обладают 4-связностью.
Трассировка окрестностей Мура
Идея
Идея, лежащая в основе трассировки окрестностей Мура (Moore-Neighbor tracing), проста;, но прежде чем объяснять её, нам нужно объяснить важное понятие: окрестности Мура пикселя.
Окрестность Мура
Окрестность Мура пикселя P — это множество из 8 пикселей, имеющих общую вершину или ребро с этим пикселем. Такие пиксели, а именно P1, P2, P3, P4, P5, P6, P7 и P8, показаны на Рисунке 1.
Окрестность Мура (Moore neighborhood, также называемая 8-соседями или indirect neighbors (непрямыми соседями)) — это важное понятие, часто упоминаемое в литературе.

Теперь мы готовы познакомиться с идеей, лежащей в основе трассировки окрестностей Мура.
Пусть существует цифровой паттерн, т.е. группа чёрных пикселей, на фоне из белых пикселей, т.е. на сетке; найдём чёрный пиксель и объявим его »начальным» пикселем. (Находить »начальный» пиксель можно разными способами, но мы, как и раньше, будем начинать с левого нижнего угла и сканировать все столбцы пикселей по порядку, пока не найдём первый чёрный пиксель, который и объявим »начальным».)
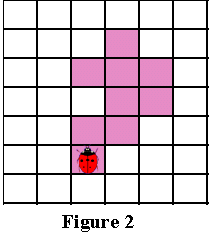
Теперь снова представьте, что вы божья коровка, стоящая на начальном пикселе, как показано на Рисунке 2 ниже. Без потери обобщённости мы будем обнаруживать контур, двигаясь вокруг паттерна по часовой стрелке. (Неважно, какое направление мы выберем, главное — использовать его в алгоритме постоянно).
Общая идея заключается в следующем: каждый раз, когда мы попадаем в чёрный пиксель P, то возвращаемся назад, то есть к белому пикселю, в котором стояли ранее. Затем обходим пиксель P по часовой стрелке, посещая каждый пиксель в его окрестности Мура, пока не попадём в чёрный пиксель. Алгоритм завершает выполнение, когда начальный пиксель достигает начального пикселя во второй раз.
Те чёрные пиксели, которые посетил алгоритм, будут контуром паттерна.
Алгоритм
Ниже приведено формальное описание алгоритма трассировки окрестностей Мура:
Входящие данные: квадратная тесселяция T, содержащая связную компоненту P из чёрных ячеек.
Выходные данные: ряд B (b1, b2,…, bk) граничных пикселей, т.е. контур.
Обозначим как M (a) окрестность Мура пикселя a.
Пусть p будет текущим граничным пикселем.
Пусть c будет текущим рассматриваемым пикселем, т.е. c находится в M (p).
Начало
- Задаём B как пустое множество.
- Снизу вверх и слева направо сканируем ячейки T, пока не найдём чёрный пиксель s из P.
- Вставим s в B.
- Зададим в качестве текущей граничной точки p точку s, т.е. p=s
- Вернёмся назад, т.е. перейдём к пикселю, из которого мы пришли в s.
- Зададим в качестве c следующий по часовой стрелке пиксель в M (p).
- Пока c не равно s, выполняем
- если c — чёрный
- Вставляем c в B
- задаём p=c
- возвращаемся назад (перемещаем текущий пиксель c в пиксель, из которого попали в p)
иначе- перемещаем текущий пиксель c в следующий по часовой стрелке пиксель в M (p)
Конец цикла «Пока»
- если c — чёрный
Конец
Демонстрация
Ниже показана анимированная демонстрация того, как трассировка окрестностей Мура выполняет обнаружение контура паттерна. (Мы решили трассировать контур по часовой стрелке.)

Анализ
Основная слабость трассировки окрестностей Мура заключается в выборе критерия останова.
В исходном описании алгоритма для трассировки окрестностей Мура критерием останова является попадание в начальный пиксель во второй раз. Аналогично алгоритму трассировки квадратов, оказывается, что трассировка окрестностей Мура при использовании такого критерия не может обнаруживать контуры большого семейства паттернов.
Ниже показана анимированная демонстрация, объясняющая, почему алгоритму не удаётся найти точный контур паттерна из-за выбора плохого критерия останова:

Как видите, усовершенствование критерия останова может стать хорошим началом для улучшения результативности трассировки в целом. Для критерия останова есть две эффективные альтернативы, аналогичные критерию останова Джейкоба.
Использование критерия Джейкоба значительно улучшает результативность трассировки окрестностей Мура, делая его наилучшим алгоритмом для определения контура любого паттерна, вне зависимости от его связности.
Причина этого в основном заключается в том, что для поиска следующего граничного пикселя алгоритм проверяет всю окрестность Мура граничного пикселя. В отличие от алгоритма трассировки квадратов, который делает повороты только влево и вправо и упускает пиксели «по диагонали», трассировка окрестностей Мура всегда будет способна обнаружить внешнюю границу любой связной компоненты. Причина заключается в следующем: для любого 8-связного (или просто связного) паттерна следующий граничный пиксель лежит в пределах окрестности Мура текущего граничного пикселя. Поскольку трассировка окрестностей Мура проверяет каждый из пикселей в окрестности Мура текущего граничного пикселя, она обязана обнаружить следующий граничный пиксель.
Когда трассировка окрестностей Мура достигает начального пикселя во второй раз точно так же, как она сделала это в первый раз, то это значит, что был обнаружен полный внешний контур паттерна, и если не остановить алгоритм, то он заново будет обнаруживать тот же контур.
Радиальная развёртка
Алгоритм радиальной развёртки (Radial Sweep) — это алгоритм обнаружения контура, рассматриваемый в некоторых книгах. Несмотря на сложное название, лежащая в его основе идея очень проста. На самом деле, оказывается, что алгоритм радиальной развёртки идентичен трассировке окрестностей Мура. Можно задаться вопросом: «Зачем же вообще мы его упоминаем?».
Трассировка окрестностей Мура выполняет поиск в окрестности Мура текущего граничного пикселя в определённом направлении (мы выбрали направление по часовой стрелке), пока не найдёт чёрный пиксель. Затем она объявляет этот пиксель текущим граничным пикселем и продолжает работу.
Алгоритм радиальной развёртки выполняет то же самое. С другой стороны, он обеспечивает интересный способ поиска следующего чёрного пикселя в окрестности Мура заданного граничного пикселя.
Способ основан на следующей идее:
каждый раз, когда мы находим новый граничный пиксель, делаем его текущим пикселем P, и рисуем воображаемый отрезок прямой, соединяющий P с предыдущим граничным пикселем. Затем поворачиваем отрезок относительно P по часовой стрелке, пока он не натолкнётся на чёрный пиксель в окрестности Мура пикселя P. Поворот отрезка идентичен проверке каждого пикселя в окрестности Мура P.
Мы создали анимированную демонстрацию того, как работает алгоритм радиальной развёртки и чем он похож на трассировку окрестностей Мура.

А когда же останавливается алгоритм радиальной развёртки?
Давайте объясним поведение алгоритма при использовании следующих критериев останова…
Критерий останова 1
Пусть алгоритм радиальной развёртки завершает работу тогда, когда посетит начальный пиксель во второй раз.
Ниже представлена анимированная демонстрация, из которой понятно, почему правильно будет сменить критерий останова.

Стоит упомянуть также то, что при использовании этого критерия останова в обоих алгоритмах результативность алгоритма радиальной развёртки идентична трассировке окрестностей Мура.
В алгоритме трассировки квадратов и в трассировке окрестностей Мура мы выяснили, что использование критерия останова Джейкоба значительно улучшает результативность обоих алгоритмов.
Критерий останова Джейкоба требует, чтобы алгоритм прекращал выполнение при посещении начального пикселя во второй раз в том же направлении, что и в первый раз.
К сожалению, мы не можем использовать в алгоритме радиальной развёртки критерий останова Джейкоба. Причина заключается в том, что алгоритм радиальной развёртки не определяет понятия «направления», в котором он попадает в граничный пиксель. Другими словами, непонятно «направление», в котором алгоритм попал в граничный пиксель (и его определение нетривиально).
Следовательно, нам нужно предложить другой критерий останова, который не зависит от направления попадания в определённый пиксель, способный улучшить результативность алгоритма радиальной развёртки…
Критерий останова 2
Допустим, что каждый раз, когда алгоритм обнаруживает новый граничный пиксель Pi, он вставляется в ряд граничных пикселей: P1, P2, P3, …, Pi; и объявляется текущим граничным пикселем. (P1 мы будем считать начальным пикселем). Это значит, что мы знаем предыдущий граничный пиксель Pi-1 каждого текущего граничного пикселя Pi . (Что касается начального пикселя, то мы будем предполагать, что P0 является воображаемым пикселем, неэквивалентным ни одному из пикселей на сетке, который стоит перед начальным пикселем в ряду граничных пикселей).
С учётом представленных выше допущений мы можем определить критерий останова следующим образом:
Алгоритм прекращает выполнение, когда:
a) текущий граничный пиксель Pi уже ранее встречался как пиксель Pj (где j < i ) в ряду граничных пикселей, И
b) Pi-1 = Pj-1.
Другими словами, алгоритм завершает выполнение тогда, когда он посещает граничный пиксель P во второй раз, если граничный пиксель до P (в ряду граничных пикселей) во второй раз является тем же пикселем, который был до P, когда P был посещён в первый раз.
Если условие критерия останова удовлетворено и алгоритм не завершает работу, то алгоритм радиальной развёртки будет продолжать обнаруживать ту же границу во второй раз.
Результативность алгоритма радиальной развёртки с этим критерием останова схоже с результативностью трассировки окрестностей Мура с критерием останова Джейкоба.
Алгоритм Тео Павлидиса
Идея
Этот алгоритм — один из самых последних алгоритмов обнаружения контуров, предложенный Тео Павлидисом. Он привёл его в своей книге 1982 года Algorithms for Graphics and Image Processing (глава 7, раздел 5). Он не так прост, как алгоритм трассировки квадратов или трассировка окрестностей Мура, но не так уж и сложен (это свойственно большинству алгоритмов обнаружения контуров).
Этот алгоритм мы будем объяснять не так, как это сделано в его книге. Наш подход легче воспринимается и он даёт представление об общей идее, лежащей в основе алгоритма.
Без утери обобщённости мы решили обходить контур по часовой стрелке, чтобы соответствовать порядку всех других алгоритмов, представленных в статье. С другой стороны, Павлидис выбрал направление против часовой стрелки. На результативность алгоритма это никак не повлияет. Единственное отличие заключается в относительном направлении движений, которые мы будем делать при обходе контура.
Теперь перейдём к идее…
Допустим, у нас есть цифровой паттерн, т.е. группа чёрных пикселей на фоне из белых пикселей, т.е. на сетке; находим чёрный пиксель и объявляем его »начальным» пикселем. Искать »начальный» пиксель можно различными способами, например, изложенным выше.
Для нахождения начального пикселя пользоваться этим способом необязательно. Вместо этого мы выберем начальный пиксель, удовлетворяющий следующим ограничениям, накладываемым на выбор начального пикселя алгоритмом Павлидиса:
Важное ограничение направления, в котором мы входим в начальный пиксель
На самом деле можно выбрать ЛЮБОЙ чёрный граничный пиксель в качестве начального при таком условии: если вы изначально стоите на нём, левый соседний пиксель НЕ чёрный. Другими словами, нужно входить в начальный пиксель в таком направлении, чтобы левый соседний пиксель был белым («левый» здесь берётся относительно направления, в котором мы входим в начальный пиксель).
Теперь представим, что вы божья коровка, стоящая на начальном пикселе, как это показано на Рисунке 1 ниже. В процессе выполнения алгоритма нас будут интересовать только три пикселя, находящиеся перед вами, т.е. P1, P2 и P3, показанные на Рисунке 1. (Мы обозначим как P2 пиксель перед вами, P1 — это пиксель слева от P2, а P3 — пиксель справа от P2).
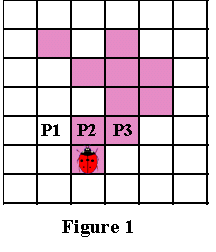
Как и в алгоритме трассировки квадратов, самое важное в алгоритме Павлидиса — это «чувство направления». Повороты влево и вправо выполняются относительно текущей позиции, которая зависит от того, как вы вошли в текущий пиксель. Следовательно, чтобы делать правильные ходы, важно отслеживать текущую ориентацию. Но как бы вы ни были расположены, пиксели P1, P2 и P3 определяются описанным выше образом.
Имея эту информацию, мы готовы к объяснению алгоритма…
Каждый раз, когда вы стоите на текущем граничном пикселе (который сначала является начальным пикселем), делаем следующее:
Во-первых, проверяем пиксель P1. Если P1 чёрный, тогда объявляем P1 текущим граничным пикселем и перемещаемся на один шаг вперёд, а затем делаем шаг влево, чтобы оказаться на P1 (порядок ходов очень важен).
На Рисунке 2 ниже показан этот случай. Путь, по которому нужно попасть в P1, показан синим.

И только если P1 белый, переходим к проверке P2…
Если P2 чёрный, то объявляем P2 текущим граничным пикселем и двигаемся на шаг вперёд, чтобы оказаться на P2. Этот случай показан на Рисунке 3 ниже. Путь, по которому нужно двигаться на P2, показан синим.

Только если и P1, и P2 белые, переходим к проверке P3…
Если P3 чёрный, то объявляем P3 текущим граничным пикселем и двигаемся на один шаг вправо, а затем на один шаг влево, как показано на Рисунке 4 ниже.
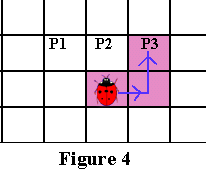
Вот и всё! Три простых правила для трёх простых случаев. Как видите, важно отслеживать своё направление при поворотах, потому что все ходы делаются относительно текущей ориентации. Но кажется, мы что-то забыли? Что если все три пикселя перед нами белые? Тогда мы поворачиваемся (стоя на текущем граничном пикселе) на 90 градусов по часовой стрелке, чтобы увидеть перед собой новый набор из трёх пикселей. Затем мы выполняем ту же проверку для этих новых пикселей. У вас может всё равно остаться вопрос: что если все эти три пикселя будут белыми?! Тогда снова поворачиваемся на 90 градусов по часовой стрелке, стоя на том же пикселе. Прежде чем проверить всю окрестность Мура пикселя, можно повернуться три раза (каждый раз на 90 градусов по часовой стрелке).
Если мы повернёмся три раза, так и не найдя чёрных пикселей, то это значит, что мы стоим на изолированном пикселе, не соединённом ни с каким другим чёрным пикселем. Именно поэтому алгоритм позволяет повернуться три раза, а потом завершает своё выполнение.
Ещё один аспект: Когда алгоритм завершает выполнение?
Алгоритм завершает работу в двух случаях:
a) как сказано выше. алгоритм позволяет повернуться три раза (каждый раз на 90 градусов по часовой стрелке), после его завершает выполнение и объявляет пиксель изолированным, ИЛИ
b) когда текущий граничный пиксель является начальным пикселем, алгоритм завершает выполнение, «объявляя», что обнаружил контур паттерна.
Алгоритм
Ниже представлено формальное описание алгоритма Павлидиса:
Входящие данные: квадратная тесселяция T, содержащая связную компоненту P чёрных ячеек.
Выходные данные: ряд B (b1, b2,…, bk) граничных пикселей, т.е. контур.
Определения:
- Обозначим как p текущий граничный пиксель, т.е. пиксель, на котором мы стоим.
- Определим P1, P2 и P3 следующим образом: (см. также
Habrahabr.ru прочитано 8774 раза