Знакомьтесь, loop fracking

Целью данной работы является обозначение еще одной техники оптимизации циклов.
При этом нет задачи ориентироваться на какую-либо существующую архитектуру, а, наоборот,
будем стараться действовать по возможности абстрактно, опираясь преимущественно на здравый смысл.
Автор назвал эту технику «loops fracking» по аналогии с, например, «loops unrolling»
или «loops nesting». Тем более, что термин отражает смысл и не занят.
Циклы являются основным объектом для оптимизации, именно в циклах большинство программ проводят основное время.
Существует достаточное количество техник оптимизации, ознакомиться с ними можно здесь.
Основные ресурсы для оптимизации это:
- Экономия на логике окончания цикла. Проверка критерия окончания цикла приводит к ветвлению, ветвление «ломает конвейер», давайте проверять реже. В результате появляются прелестные образцы кода, например, Duf«s device.
На данный момент предсказатели переходов (там, где они есть) в процессорах сделали подобную оптимизацию малоэффективной.void send(int *to, int *from, int count) { int n = (count + 7) / 8; switch (count % 8) { case 0: do { *to = *from++; case 7: *to = *from++; case 6: *to = *from++; case 5: *to = *from++; case 4: *to = *from++; case 3: *to = *from++; case 2: *to = *from++; case 1: *to = *from++; } while (--n > 0); } } - Вынос инвариантов цикла за скобки (hoisting).
- Оптимизация работы с памятью для более эффективной работы кэша памяти. Если в цикле есть обращения к количеству памяти, заведомо превышающему объем кэш-памяти, становится важным, в каком порядке идут эти обращения. Компилятору сложно кроме очевидных случаев разбираться с этим, иногда для достижения эффекта фактически пишется другой алгоритм. Поэтому данная оптимизация ложится на плечи прикладных программистов. А компилятор / профилировщик могут обеспечить статистикой, дать подсказки … обратную связь.
- Использование (явного или неявного) параллелизма процессора. Современные процессоры умеют исполнять код параллельно.
В случае явно параллельной архитектуры (EPIC, VLIW) одна инструкция может содержать несколько команд (которые будут выполняться параллельно), затрагивающих разные функциональные блоки.
Суперскалярные процессоры самостоятельно разбирают поток инструкций, выискивают параллелизм и по возможности его используют.
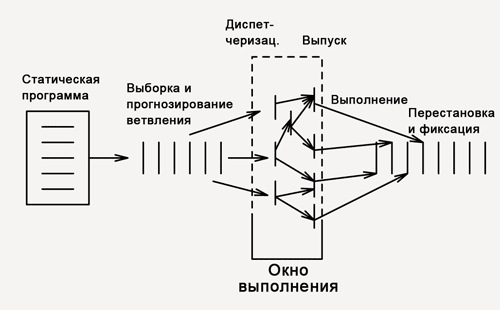
Принципиальная схема суперскалярного исполнения командЕще один вариант — векторные операции, SIMD.
Сейчас мы как раз и займемся поиском способа максимального использования параллелизма процессора (ов).
Что мы имеем.
Для начала разберем несколько простых примеров, используя для опытов MSVS-2013(x64) на процессоре Intel Core-i7 2600. К слову, GCC умеет всё то же и не хуже, во всяком случае на таких простых примерах.
Простейший цикл — вычисление суммы целочисленного массива.
int64_t data[100000];
…
int64_t sum = 0;
for (int64_t val : data) {
sum += val;
}
Вот что делает из этого компилятор:
lea rsi,[data]
mov ebp,186A0h ;100 000
mov r14d,ebp
...
xor edi,edi
mov edx,edi
nop dword ptr [rax+rax] ; выравнивание
loop_start:
add rdx,qword ptr [rsi]
lea rsi,[rsi+8]
dec rbp
jne loop_start
То же, но с double«ами (AVX, /fp: precise & /fp: strict — ANSI совместимость)
vxorps xmm1,xmm1,xmm1
lea rax,[data]
mov ecx,186A0h
nop dword ptr [rax+rax]
loop_start:
vaddsd xmm1,xmm1,mmword ptr [rax]
lea rax,[rax+8]
dec rcx
jne loop_start
Миллион раз этот код выполняется за 85 сек.
Не видно здесь никакой работы компилятора по выявлению параллельности, хотя,
казалось бы, в задаче она налицо. Компилятор обнаружил зависимость в данных и не смог ее обойти.
То же, но (AVX, /fp: fast — без ANSI — совместимости)
vxorps ymm2,ymm0,ymm0
lea rax,[data]
mov ecx,30D4h ; 12500, 1/8
vmovupd ymm3,ymm2
loop_start:
vaddpd ymm1,ymm3,ymmword ptr [rax+20h] ; SIMD
vaddpd ymm2,ymm2,ymmword ptr [rax]
lea rax,[rax+40h]
vmovupd ymm3,ymm1
dec rcx
jne loop_start
vaddpd ymm0,ymm1,ymm2
vhaddpd ymm2,ymm0,ymm0
vmovupd ymm0,ymm2
vextractf128 xmm4,ymm2,1
vaddpd xmm0,xmm4,xmm0
vzeroupper
Выполняется 26 сек, используются векторные операции.
Тот же цикл, но в традиционном С стиле
for (i = 0; i < 100000; i ++) {
sum += data[i];
}
Получаем неожиданно для (/fp: precise)
vxorps xmm4,xmm4,xmm4
lea rax,[data+8h]
lea rcx,[piecewise_construct+2h]
vmovups xmm0,xmm4
nop word ptr [rax+rax]
loop_start:
vaddsd xmm0,xmm0,mmword ptr [rax-8]
add rax,50h
vaddsd xmm1,xmm0,mmword ptr [rax-50h]
vaddsd xmm2,xmm1,mmword ptr [rax-48h]
vaddsd xmm3,xmm2,mmword ptr [rax-40h]
vaddsd xmm0,xmm3,mmword ptr [rax-38h]
vaddsd xmm1,xmm0,mmword ptr [rax-30h]
vaddsd xmm2,xmm1,mmword ptr [rax-28h]
vaddsd xmm3,xmm2,mmword ptr [rax-20h]
vaddsd xmm0,xmm3,mmword ptr [rax-18h]
vaddsd xmm0,xmm0,mmword ptr [rax-10h]
cmp rax,rcx
jl loop_start
Здесь нет параллельности, всего лишь попытка сэкономить на обслуживании цикла.
Выполняется этот код 87 сек.
Для /fp: fast код не изменился.
Подскажем компилятору, используя loop nesting.
double data[100000];
…
double sum = 0, sum1 = 0, sum2 = 0;
for (int ix = 0; i < 100000; i+=2)
{
sum1 += data[i];
sum2 += data[i+1];
}
sum = sum1 + sum2;
Получаем ровно то, что просили, причем код одинаков для опций /fp: fast & /fp: precise.
Операции vaddsd на некоторых процессорах (Бульдозер от АМД) могут выполняться параллельно.
vxorps xmm0,xmm0,xmm0
vmovups xmm1,xmm0
lea rax,[data+8h]
lea rcx,[piecewise_construct+2h]
nop dword ptr [rax]
nop word ptr [rax+rax]
loop_start:
vaddsd xmm0,xmm0,mmword ptr [rax-8]
vaddsd xmm1,xmm1,mmword ptr [rax]
add rax,10h
cmp rax,rcx
jl loop_start
Миллион раз этот код выполняется за 43 сек, вдвое быстрее чем «наивный и точный» подход.
При шаге в 4 элемента код выглядит так (опять же, одинаково для опций компилятора /fp: fast & /fp: precise)
vxorps xmm0,xmm0,xmm0
vmovups xmm1,xmm0
vmovups xmm2,xmm0
vmovups xmm3,xmm0
lea rax,[data+8h]
lea rcx,[piecewise_construct+2h]
nop dword ptr [rax]
loop_start:
vaddsd xmm0,xmm0,mmword ptr [rax-8]
vaddsd xmm1,xmm1,mmword ptr [rax]
vaddsd xmm2,xmm2,mmword ptr [rax+8]
vaddsd xmm3,xmm3,mmword ptr [rax+10h]
add rax,20h
cmp rax,rcx
jl loop_start
vaddsd xmm0,xmm1,xmm0
vaddsd xmm1,xmm0,xmm2
vaddsd xmm1,xmm1,xmm3
Этот код миллион раз выполняется за 34 сек.
Для того же, чтобы гарантировать векторные вычисления, придется прибегать к разным трюкам, как то
- писать подсказки компилятору в виде прагм: #pragma ivdep (#pragma loop (ivdep), #pragma GCC ivdep), #pragma vector always, #pragma omp simd… и надеяться что компилятор не проигнорирует их
- использовать intrinsic«и — указания компилятору, какие инструкции использовать, например, суммирование двух массивов может выглядеть так:
Как то всё это не очень вяжется со светлым образом «языка высокого уровня».
С одной стороны, при необходимости получить результат, указанные оптимизации совсем не в тягость.
С другой, возникает проблема переносимости. Допустим, программа писалась и отлаживалась для процессора с четырьмя сумматорами.
Тогда при попытке исполнить ее на версии процессора с 6-ю сумматорами, мы не получим ожидаемого выигрыша.
А на версии с тремя — получим замедление в 2 раза, а не на четверть, как хотелось бы.
Напоследок вычислим сумму квадратов (/fp: precise)
vxorps xmm2,xmm2,xmm2
lea rax,[data+8h] ; pdata = &data[1]
mov ecx,2710h ; 10 000
nop dword ptr [rax+rax]
loop_start:
vmovsd xmm0,qword ptr [rax-8] ; xmm0 = pdata[-1]
vmulsd xmm1,xmm0,xmm0 ; xmm1 = pdata[-1] ** 2
vaddsd xmm3,xmm2,xmm1 ; xmm3 = 0 + pdata[-1] ** 2 ; sum
vmovsd xmm2,qword ptr [rax] ; xmm2 = pdata[0]
vmulsd xmm0,xmm2,xmm2 ; xmm0 = pdata[0] ** 2
vaddsd xmm4,xmm3,xmm0 ; xmm4 = sum + pdata[0] ** 2 ; sum
vmovsd xmm1,qword ptr [rax+8] ; xmm1 = pdata[1]
vmulsd xmm2,xmm1,xmm1 ; xmm2 = pdata[1] ** 2
vaddsd xmm3,xmm4,xmm2 ; xmm3 = sum + pdata[1] ** 2 ; sum
vmovsd xmm0,qword ptr [rax+10h] ; ...
vmulsd xmm1,xmm0,xmm0
vaddsd xmm4,xmm3,xmm1
vmovsd xmm2,qword ptr [rax+18h]
vmulsd xmm0,xmm2,xmm2
vaddsd xmm3,xmm4,xmm0
vmovsd xmm1,qword ptr [rax+20h]
vmulsd xmm2,xmm1,xmm1
vaddsd xmm4,xmm3,xmm2
vmovsd xmm0,qword ptr [rax+28h]
vmulsd xmm1,xmm0,xmm0
vaddsd xmm3,xmm4,xmm1
vmovsd xmm2,qword ptr [rax+30h]
vmulsd xmm0,xmm2,xmm2
vaddsd xmm4,xmm3,xmm0
vmovsd xmm1,qword ptr [rax+38h]
vmulsd xmm2,xmm1,xmm1
vaddsd xmm3,xmm4,xmm2
vmovsd xmm0,qword ptr [rax+40h]
vmulsd xmm1,xmm0,xmm0
vaddsd xmm2,xmm3,xmm1 ; xmm2 = sum;
lea rax,[rax+50h]
dec rcx
jne loop_start
Компилятор опять пилит цикл на куски по 10 элементов с целью экономии на логике цикла,
при этом обходится 5 регистрами — один под сумму и по паре на каждую из двух параллельных веток умножений.
Или вот так для /fp: fast
vxorps ymm4,ymm0,ymm0
lea rax,[data]
mov ecx,30D4h ;12500 1/8
loop_start:
vmovupd ymm0,ymmword ptr [rax]
lea rax,[rax+40h]
vmulpd ymm2,ymm0,ymm0 ; SIMD
vmovupd ymm0,ymmword ptr [rax-20h]
vaddpd ymm4,ymm2,ymm4
vmulpd ymm2,ymm0,ymm0
vaddpd ymm3,ymm2,ymm5
vmovupd ymm5,ymm3
dec rcx
jne loop_start
vaddpd ymm0,ymm3,ymm4
vhaddpd ymm2,ymm0,ymm0
vmovupd ymm0,ymm2
vextractf128 xmm4,ymm2,1
vaddpd xmm0,xmm4,xmm0
vzeroupper
Сводная таблица:
| MSVC,/fp: strict, /fp: precise, сек | MSVC,/fp: fast, сек | |
| foreach | 85 | 26 |
| C style цикл | 87 | 26 |
| C style nesting X2 | 43 | 43 |
| C style nesting X4 | 34 | 34 |
Как объяснить эти числа?
Стоит отметить, что истинную картину происходящего знают только разработчики процессора, мы же можем только делать догадки.
Первая мысль, что ускорение происходит за счет нескольких независимых сумматоров, по всей видимости ошибочна.
Процессор i7–2600 имеет один векторный сумматор, который не умеет выполнять независимые скалярные операции.
Тактовая частота процессора — до 3.8 гГц.
85 сек простого цикла дают нам (миллион раз по 100 000 сложений) ~3 такта на итерацию. Это хорошо согласуется с данными (1, 2) о 3 тактах на исполнение векторной инструкции vaddpd (пусть даже мы складываем скаляры). Поскольку есть зависимость по данным, быстрее 3 тактов итерацию выполнить невозможно.
В случае нестинга (Х2) отсутствует зависимость по данным внутри итерации и есть возможность загрузить конвейер сумматора с разницей в такт. Но в следующей итерации зависимости по данным возникают так же с разницей в такт, в результате имеем ускорение в 2 раза.
В случае нестинга (Х4) конвейер сумматора загружается также с шагом в такт, но ускорения в 3 раза (из-за длины конвейера) не происходит, вмешивается дополнительный фактор. Например, итерация цикла перестала умещаться в строке кэша L0m и получает штрафной такт (ы).
Итак:
- с моделью компиляции /fp: fast самый простой исходный текст дает самый быстрый вариант кода, что логично т.к. мы имеем дело с языком высокого уровня.
- ручные оптимизации в духе nesting«а дают хороший результат для модели /fp: precise, но только мешают компилятору при использовании /fp: fast
- ручные оптимизации переносимы в большей степени, нежели векторизованный код
Чуть чуть про компиляторы.
Регистровые архитектуры дают простой и универсальный способ получить приемлемый код
из переносимого текста на языках высокого уровня.
Компиляцию условно можно разбить на несколько шагов:
- Синтаксический анализ. На этом этапе осуществляется синтаксически управляемая трансляция, производятся статические проверки. На выходе мы имеем дерево (DAG) синтаксического разбора.
- Генерация промежуточного кода. При желании, генерация промежуточного кода может быть объединена с синтаксическим анализом.
Тем более, что при использовании в качестве промежуточного кода трехадресных инструкций, данный шаг становится тривиальным ибо «трехадресный код является линеаризованным представлением синтаксического дерева или дага, в котором внутренним узлам графа соответствуют явные имена».
В сущности, трехадресный код предназначен для виртуального процессора с бесконечным количеством регистров. - Генерация кода. Результатом данного шага является программа для целевой архитектуры. Поскольку реальное количество регистров ограничено и невелико, на этом этапе мы должны определить, какие временные переменные в каждый момент будут находиться в регистрах, и распределить их по конкретным регистрам. Даже в чистом виде эта задача является NP-полной, кроме того, дело усложняется тем, что обычно существуют разнообразные ограничения по использованию регистров. Тем не менее, для решения данной задачи разработаны приемлемые эвристики. Кроме того, трехадресный (или его эквиваленты) код дает нам формальный аппарат для анализа потоков данных, оптимизации, удаления бесполезного кода, …
Вырисовываются проблемы:
- Для решения NP-полной задачи размещения регистров используют эвристики и это даёт код приемлемого качества. Эти эвристики не любят дополнительных ограничений на использование памяти или регистров. Например, расщепленной (interlaced) памяти, неявного использования регистров инструкциями, векторных операций, регистровых колец … Не любят вплоть до того, что эвристика может перестать работать и построение близкого к оптимальному кода перестает быть задачей, решаемой универсальным образом.
В результате (векторные?) возможности процессора могут быть задействованы лишь тогда, когда компилятор распознал типовую ситуацию из набора, которому его обучили. - Проблема масштабирования. Размещение (allocation) регистров делается статически, если мы попытаемся исполнить скомпилированный код на процессоре с той же системой команд, но большим количеством регистров, никакого выигрыша не получится.
Это касается и SPARC с его стеком регистровых окон, для которого большее количество регистров приводит лишь к тому, что большее количество фреймов вызовов умещается в пуле регистров, что уменьшает частоту обращений к памяти.
EPIC — сделана попытка в направлении масштабирования — «Каждая группа из нескольких инструкций называется bundle. Каждый bundle может иметь стоповый бит, обозначающий, что следующая группа зависит от результатов работы данной. Такой бит позволяет создавать будущие поколения архитектуры с возможностью параллельного запуска нескольких bundles. Информация о зависимостях вычисляется компилятором, и поэтому аппаратуре не придётся проводить дополнительную проверку независимости операндов.» Предполагалось, что независимые bundles могут исполняться параллельно, причем, чем больше исполняющих устройств в системе, тем шире может использоваться внутренний параллелизм программы. С другой стороны, далеко не всегда подобные особенности дают выигрыш, во всяком случае, для суммирования массива это видится автору бесполезным.
Суперскалярные процессоры решают проблему, вводя «регистры для нас» и «регистры в себе». На число первых ориентируется компилятор, когда расписывает (аллоцирует) регистры. Число вторых может быть любым, обычно их в разы больше, чем первых. В процессе декодирования суперскалярный процессор заново расписывает регистры исходя из их фактического количества в пределах окна в теле программы. Размер окна определяется сложностью логики, которую процессор может себе позволить. Кроме числа регистров, конечно, масштабированию подлежат и функциональные устройства.
- Проблема совместимости. Особо отметим X84–64 и линейку технологий — SSE — SSE2 — SSE3 — SSSE3 — SSE4 — AVX — AVX2 — AVX512 — …
Совместимость сверху вниз (т.е. код скомпилирован под старшую технологию, а хочется исполнять на младших процессорах) может быть обеспечена одним способом — генерацией кода под каждую упомянутую технологию и выбор в runtime нужной ветки для исполнения. Звучит не очень привлекательно.
Совместимость снизу вверх обеспечивает процессор. Эта совместимость гарантирует исполнимость кода, но не обещает его эффективного исполнения. Например, если код скомпилирован под технологию с двумя независимыми сумматорами, а исполняется на процессоре с 4-мя, фактически использованы будут только два из них. Генерация нескольких веток кода под разные технологии не решает проблемы будущих технологий, планируемых или нет.
Взгляд на циклы
Рассмотрим ту же задачу, суммирование массива. Представим это суммирование как вычисление одного выражения. Поскольку мы используем бинарное сложение, выражение может быть представлено в виде бинарного дерева, причем из за ассоциативности суммирования, таких деревьев много.
Вычисление производится при обходе дерева вглубь слева направо.
Обычное суммирование выглядит как лево-растущее вырожденное до списка дерево: 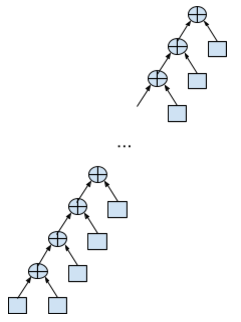
double data[N];
…
double sum = 0;
for (int i = 0; i < N; i++)
{
sum += data[i];
}
Максимальная глубина стека (обход в глубину подразумевает постфиксное суммирование, т.е. стек), которая может здесь потребоваться — 2 элемента. Никакой параллельности не предполагается, каждое суммирование (кроме первого) должно дождаться результатов предыдущего суммирования, т.е. налицо зависимость по данным.
Зато нам достаточно 3 регистров (сумма и два для эмуляции верхушки стека) чтобы просуммировать массив любого размера.
Нестинг цикла в два ручейка выглядит так: 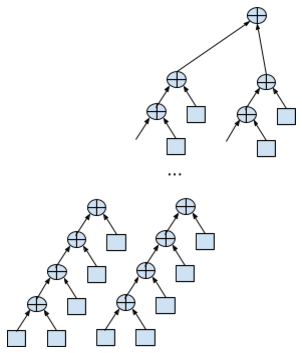
double data[N];
…
double sum = 0;
double sum1 = 0, sum2 = 0;
for (int i = 0; i < N/2; i+=2)
{
sum1 += data[i];
sum2 += data[i + 1];
}
sum = sum1 + sum2;
Для вычислений нужно вдвое больше ресурсов, 5 регистров на всё,
но теперь часть суммирований можно делать параллельно.
Самый ужасный с вычислительной точки зрения вариант — право-растущее, вырожденное до списка дерево, для его вычисления нужен стек размером с массив при отсутствии параллелизма.
Какой вариант дерева даст максимальный параллелизм? Очевидно, сбалансированное (в пределах возможного) дерево, где обращения к исходным данным есть только в листовых суммирующих узлах.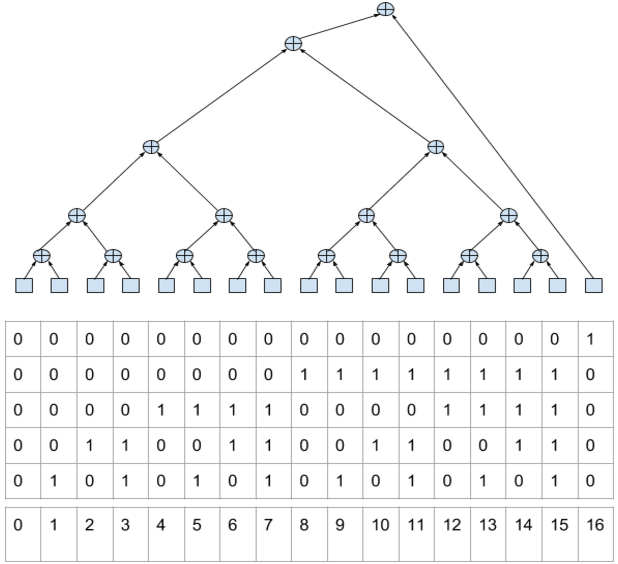
// Алгоритм вычисления суммы таков:
double data[N];
for (unsigned ix = 0; ix < N; ix++) {
unsigned lix = ix;
push(data[ix]);
while (lix & 1) {
popadd();
lix >>= 1;
}
}
for (unsigned ix = 1; ix < bit_count(N+1); ix++) {
popadd();
}
В этом псевдо-коде использованы следующие функции:
- push(val) — помещает значение на вершину стека, увеличивает стек. Предполагается что стек организован на пуле регистров.
- popadd() — суммирует два элемента на вершине стека, результат помещает во второй сверху, удаляет верхний элемент.
- bit_count(val) — подсчитывает число бит в целочисленном значении
После работы этого псевдокода в стеке остается единственный элемент, равный искомой сумме.
Как это работает? Обратим внимание, что номер элемента в бинарном представлении кодирует путь до него от вершины дерева выражения (от старших битов к младшим). При этом 0 обозначает движение налево, 1 — направо (аналогично коду Хаффмана).
Отметим, что количество непрерывно идущих взведённых младших бит равно количеству суммирований, которые надо сделать для обработки текущего элемента. А общее количество взведённых бит в номере означает количество элементов находящихся в стеке на момент до начала работы с эти элементом.
На что следует обратить внимание:
- Размер стека т.е. потребное число регистров для него есть log2 от размера данных. С одной стороны, это не очень удобно т.к. размер данных может быть величиной вычисляемой, а размер стека хотелось бы определить при компиляции. С другой стороны, никто на мешает компилятору пилить данные на тайлы размер которых определяется исходя из числа доступных регистров.
- В такой интерпретации задачи достаточно параллелизма, чтобы автоматически задействовать любое количество доступных независимых сумматоров. Загрузка элементов из массива может делаться независимо и параллельно. Суммирования одного уровня также выполняются параллельно.
- с параллелизмом есть проблемы. Пусть на момент компиляции у нас было N сумматоров. Для того, чтобы эффективно работать с отличным от N их числом (ради чего всё и затевалось), придётся задействовать аппаратную поддержку
- для архитектур с явным параллелизмом всё непросто. Помог бы пул сумматоров и разрешение исполнять параллельно несколько независимых «широких» инструкций. Для суммирования берется не конкретный сумматор, а первый в очереди. Если широкая инструкция пытается выполнить три суммирования, из пула будут истребованы три сумматора. Если такого к-ва свободных сумматоров нет, инструкция будет блокирована вплоть до их освобождения.
- для суперскалярных архитектур требуется отслеживать состояние стека. Есть унарные (ex: смена знака) и бинарные операции (Ex: popadd) со стеком. А также листовые операции без зависимостей (Ex: push). С последними проще всего, их можно ставить на исполнение в любой момент. Но если у операции есть аргумент (ы), она перед выполнением должна дождаться готовности своих аргументов.
Так, оба значения для операции popadd должны находиться на вершине стека. Но к тому моменту как подойдет очередь их суммировать, они уже могут быть совсем не на вершине стека. Может случиться, что они физически расположены и не подряд.
Выходом будет размещение (allocation) соответствующего регистра из пула стека в момент постановки инструкции на исполнение, а не в момент, когда результат готов и его надо разместить.
Например push (data[i]) означает, что из памяти надо вычитать значение и разместить его в регистр. Номер этого регистра берется из очереди свободных регистров до начала чтения. Регистр удалятся из очереди.
Для операции popadd на момент постановки на исполнение номера регистров с аргументами уже известны, хотя, возможно и не вычислены. При этом берется новый регистр под результат, а при готовности аргументов popadd исполняется, регистры из под аргументов отдаются в очередь свободных.
Постановка инструкций на исполнение происходит вплоть до исчерпания пула регистров и по мере их освобождения продвигается вперед.
Таким образом достигается масштабируемость и по размеру пула регистров и по количеству функциональных устройств. Платой является поддержание состояния стека/очереди регистров и зависимостей между инструкциями. Что не выглядит непреодолимой преградой.
- В режиме ANSI совместимости из-за проблем с точностью для выражений с double«ами формально невозможны оптимизационные алгебраические преобразования. Поэтому существует режим /fp: fast, который развязывает компилятору руки. Фактически суммирование пирамидкой даже более бережно относится к точности в силу того, что происходит суммирование (более вероятно) сопоставимых чисел, а не добавление к нарастающей сумме.
- Можно ли реализовать описанную схему на существующих архитектурах, без аппаратной поддержки стека? Да, для фиксированного размера массива. Компилятор пилит цикл на тайлы размером, скажем, 64 элемента и явно расписывает стековую машину по регистрам. Заодно потребуется и код для остальных степеней 2 меньше 64 — для выхода из цикла. Это будет довольно громоздко, но сработает.
Так может выглядеть код для 16 -элементной пирамиды.lea rax,[data] vxorps xmm6,xmm6,xmm6 ; здесь будем держать 0 vaddsd xmm0,xmm6,mmword ptr [rax] ; 0 vaddsd xmm1,xmm0,mmword ptr [rax+8] ; 1 vaddsd xmm0,xmm6,mmword ptr [rax+10h] ; 1 0 vaddsd xmm2,xmm0,mmword ptr [rax+18h] ; 1 2 vaddsd xmm0,xmm1,xmm2 ; 0 vaddsd xmm1,xmm6,mmword ptr [rax+20h] ; 0 1 vaddsd xmm2,xmm1,mmword ptr [rax+28h] ; 0 2 vaddsd xmm1,xmm6,mmword ptr [rax+30h] ; 0 2 1 vaddsd xmm3,xmm1,mmword ptr [rax+38h] ; 0 2 3 vaddsd xmm1,xmm2,xmm3 ; 0 1 vaddsd xmm0,xmm0,xmm1 ; 0 vaddsd xmm1,xmm6,mmword ptr [rax+40h] ; 0 1 vaddsd xmm2,xmm1,mmword ptr [rax+48] ; 0 2 vaddsd xmm1,xmm6,mmword ptr [rax+50h] ; 0 2 1 vaddsd xmm3,xmm1,mmword ptr [rax+58h] ; 0 2 3 vaddsd xmm1,xmm2,xmm3 ; 0 1 vaddsd xmm2,xmm6,mmword ptr [rax+60h] ; 0 1 2 vaddsd xmm3,xmm2,mmword ptr [rax+68h] ; 0 1 3 vaddsd xmm2,xmm6,mmword ptr [rax+70h] ; 0 1 3 2 vaddsd xmm4,xmm2,mmword ptr [rax+78h] ; 0 1 3 4 vaddsd xmm2,xmm4,xmm3 ; 0 1 2 vaddsd xmm3,xmm1,xmm2 ; 0 3 vaddsd xmm1,xmm0,xmm3 ; 1
Что дальше?
Мы разобрали нахождение суммы массива — очень простую задачу. Возьмем что-нибудь посложнее.
Последний пример достаточно показателен. В целях оптимизации рекурсия обычно переводится в итерации, в результате типичный текст (основной цикл) выглядит так:
nn = N >> 1;
ie = N;
for (n=1; n<=LogN; n++) {
rw = Rcoef[LogN - n];
iw = Icoef[LogN - n];
if(Ft_Flag == FT_INVERSE) iw = -iw;
in = ie >> 1;
ru = 1.0;
iu = 0.0;
for (j=0; j>= 1;
}
Что можно сделать в данном случае? В духе описанной оптимизации циклов, пожалуй, что ничего. Может ли здесь быть полезным описанный аппаратный стек, вопрос интересный. Впрочем, это уже совсем другая история.
PS: отдельное спасибо Таситу Мурки (Felid) за консультации по SIMD и не только.
PPS: иллюстрация для заголовка взята из видеоряда к King Crimson — Fracture — Live in Boston 1974.
