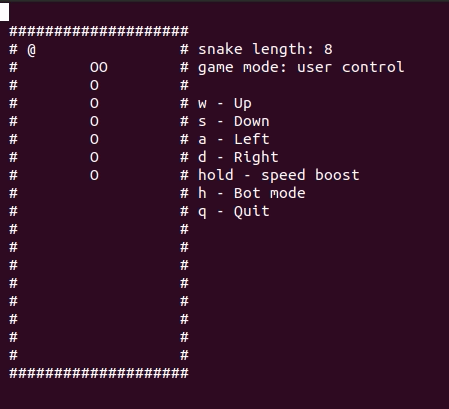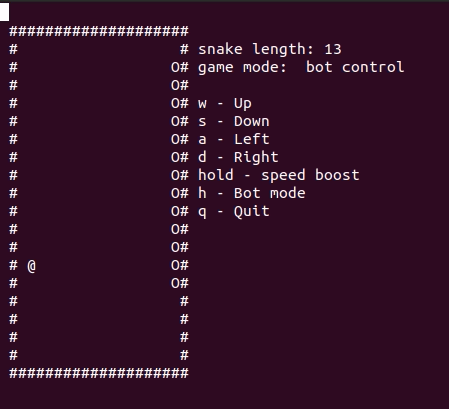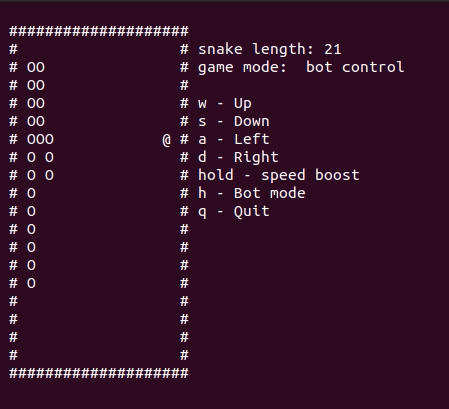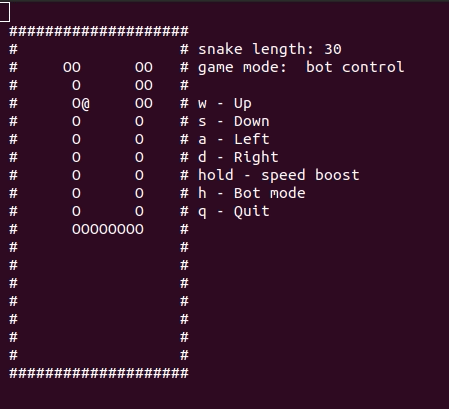
Змейка на Haskell с циклом Гамильтона
После прохождения курса по Haskell решил закрепить знания первым проектом. Писать будем змейку для терминала. Чтобы придать игре уникальности, добавим бота, который сам будет проходить игру.

Проект написан на haskell-platform, Ubuntu 20.04.
GitHub проекта
Игровой цикл
Начнем с реализации игрового цикла. Змея может двигаться независимо от нажатия клавиш, следовательно нам понадобится два параллельных потока. Используем модуль Control.Concurrent. Ответвляемся от основного процесса при помощи forkIO и синхронизируем потоки через MVar. С каждой итерацией игрового цикла, tryInput будет содержать Maybe Char значение, в зависимости от ввода пользователя. Потоки при этом не блокируются и работают параллельно. Для настройки буферизации ввода воспользуемся System.IO — отключим ожидание EOL символа при вводе и уберем отображение пользовательского вывода. Интересно, что hSetBuffering stdin NoBuffering не работает для Windows консоли — getChar будет ждать EOL и запустить игру в форточках в текущем виде не получится. Также подключим System.Console.ANSI для очистки экрана и перемещения курсора терминала.
import Control.Concurrent
import System.Console.ANSI
import System.IO
gameLoop :: ThreadId -> MVar Char -> IO ()
gameLoop inputThId input = do
tryInput <- tryTakeMVar input
gameLoop inputThId input
inputLoop :: MVar Char -> IO ()
inputLoop input = (putMVar input =<< getChar) >> inputLoop input
main = do
hSetBuffering stdin NoBuffering
hSetEcho stdin False
clearScreen
input <- newEmptyMVar
inputThId <- forkIO $ inputLoop input
gameLoop inputThId inputМир для змеи
Определим типы данных. У игры будет 4 состояния: Process — змеей управляет игрок, Bot — змеей рулит игра, GameOver и Quit. Мир игры определен типом data World, он будет каким-то образом меняться в игровом цикле gameLoop. Сейчас он содержит змею, направление ее движения, координату фрукта и текущее игровое состояние. Далее по мере разработки будет добавлять в него новые поля. Начальная точка (0,0) будет верхним левым краем консоли. Змея двигается параллельно осям, следовательно у нас 4 возможных направления движения.
data StepDirection = DirUp
| DirDown
| DirLeft
| DirRight deriving (Eq)
type Point = (Int, Int)
type Snake = [Point]
data WorldState = Process
| GameOver
| Quit
| Bot deriving (Eq)
data World = World { snake :: Snake
, direction :: StepDirection
, fruit :: Point
, worldState :: WorldState
}
gameLoop :: ThreadId -> MVar Char -> World -> IO ()
{-- … --}Таймер
Для анимации движения змеи нам потребуются функции работы со временем. Воспользуемся модулем Data.Time.Clock. Добавим в наш мир 3 поля: lastUpdateTime — время последнего обновления мира, updateDelay — сколько ждем до следующего обновления и isUpdateIteration — флаг необходимости обновить мир в текущей итерации. Укажем начальные значения мира и напишем для него первый обработчик timerController. Он принимает текущее время и устанавливает флаг isUpdateIteration, если пришло время обновляться.
import Data.Time.Clock
data World = World {
{-- … --}
, lastUpdateTime :: UTCTime
, updateDelay :: NominalDiffTime
, isUpdateIteration :: Bool
}
initWorld :: UTCTime -> World
initWorld timePoint = World { snake = [(10, y) | y <- [3..10]]
, direction = DirRight
, fruit = (3, 2)
, lastUpdateTime = timePoint
, updateDelay = 0.3
, isUpdateIteration = True
, worldState = Process
}
timerController :: UTCTime -> World -> World
timerController timePoint world
| isUpdateTime timePoint world = world { lastUpdateTime = timePoint
, isUpdateIteration = True
}
| otherwise = world where
isUpdateTime timePoint world =
diffUTCTime timePoint (lastUpdateTime world) >= updateDelay world
gameLoop inputThId input oldWorld = do
{-- … --}
timePoint <- getCurrentTime
let newWorld = timerController timePoint oldWorld
gameLoop inputThId input newWorld { isUpdateIteration = False }
main = do
{-- … --}
timePoint <- getCurrentTime
gameLoop inputThId input (initWorld timePoint)Контроллер ввода
Далее добавим обработчик ввода inputController. Клавиши WSAD меняют направление нашей змеи. Стоит обратить внимание, что змея не может двигаться назад, за исключением случая, когда она состоит из 1 сегмента. Поэтому если новое направление ведет ко второму от головы сегменту змеи, мы игнорируем такой ввод. Также если текущее направление совпадает с предыдущим, то есть пользователь зажал клавишу управления, ускорим движение змеи уменьшив updateDelay. Функция pointStep принимает направление и точку, возвращая новую точку, перемещенную на один шаг в заданном направлении.
pointStep :: StepDirection -> Point -> Point
pointStep direction (x, y) = case direction of
DirUp -> (x, y - 1)
DirDown -> (x, y + 1)
DirLeft -> (x - 1, y)
DirRight -> (x + 1, y)
inputController :: Maybe Char -> World -> World
inputController command world = let
boost dir1 dir2 = if dir1 == dir2 then 0.05 else 0.3
filterSecondSegmentDir (x:[]) dirOld dirNew = dirNew
filterSecondSegmentDir (x:xs) dirOld dirNew | pointStep dirNew x == head xs = dirOld
| otherwise = dirNew in
case command of
Just 'w' -> world { direction = filterSecondSegmentDir (snake world) (direction world) DirUp
, updateDelay = boost (direction world) DirUp
, worldState = Process
}
Just 's' -> world { direction = filterSecondSegmentDir (snake world) (direction world) DirDown
, updateDelay = boost (direction world) DirDown
, worldState = Process
}
Just 'a' -> world { direction = filterSecondSegmentDir (snake world) (direction world) DirLeft
, updateDelay = boost (direction world) DirLeft
, worldState = Process
}
Just 'd' -> world { direction = filterSecondSegmentDir (snake world) (direction world) DirRight
, updateDelay = boost (direction world) DirRight
, worldState = Process
}
Just 'q' -> world { worldState = Quit }
Just 'h' -> world { worldState = Bot }
_ -> world { updateDelay = 0.3 }Двигаем змею
Следующий контроллер moveController сдвинет нашу змею, если пришло время isUpdateIteration для обновления мира.
snakeStep :: StepDirection -> Snake -> Snake
snakeStep direction snake = (pointStep direction $ head snake):(init snake)
moveController :: World -> World
moveController world
| not $ isUpdateIteration world = world
| otherwise = world { snake = snakeStep (direction world) (snake world) }Столкновения с препятствиями
Границы поля
Последний контроллер будет обрабатывать столкновения змеи с препятствиями. В текущий момент ими могут быть только сама змея и фрукт, поэтому добавим стены. Они статичны, поэтому не будет добавлять их в мир и объявим отдельно. Первый элемент пары (1,1) — верхняя левая точка стены и (20,20) — нижняя правая.
initWalls :: Walls
initWalls = ((1,1),(20,20))ГСЧ
Фрукт появляется на поле в случайном месте, следовательно нам нужен ГСЧ. В Haskell он реализован в модуле System.Random, функция randomR. Так как мы работаем с чистыми функциями, которые возвращают при одинаковых аргументах одинаковый результат, вторым аргументом randomR служит генератор, который обновляется с каждым вызовом. Добавим его как поле нашего мира и зададим ему начальное значение. Когда змея ест фрукт, она растет в хвосте. Сохраним координату крайней точки хвоста при обновлении мира.
import System.Random
data World = World {
{-- … --}
, oldLast :: Point
, rand :: StdGen
}
initWorld timePoint = World {
{-- … --}
, oldLast = (0, 0)
, rand = mkStdGen 0
}
{-- … --}
timerController timePoint world
| isUpdateTime timePoint world = world {
{-- … --}
, oldLast = last $ snake world
}
{-- … --} Контроллер столкновений
Добавим функции проверки столкновений змеи с телом и головы со стеной.
collisionSnake :: Snake -> Bool
collisionSnake (x:xs) = any (== x) xs
collisionWall :: Point -> Walls -> Bool
collisionWall (sx,sy) ((wx1,wy1),(wx2,wy2)) =
sx <= wx1 || sx >= wx2 || sy <= wy1 || sy >= wy2Все готово для контроллера столкновений collisionController. Переводим состояние мира в GameOver при столкновении с препятствиями и увеличим длину змеи в хвосте при съедании фрукта, также сгенерив новый в пределах стен. Если координата нового фрукта является координатой тела змеи, пробуем новую координату.
collisionController :: World -> World
collisionController world
| not $ isUpdateIteration world = world
| collisionSnake $ snake world = world { worldState = GameOver }
| collisionWall (head $ snake world) initWalls = world { worldState = GameOver }
| collisionFruit (snake world) (fruit world) = world { snake =
(snake world) ++ [oldLast world]
, fruit = newFruit
, rand = newRand
}
| otherwise = world where
collisionFruit snake fruit = fruit == head snake
(newFruit, newRand) = freeRandomPoint world (rand world)
randomPoint ((minX, minY), (maxX, maxY)) g = let
(x, g1) = randomR (minX + 1, maxX - 1) g
(y, g2) = randomR (minY + 1, maxY - 1) g1 in
((x, y), g2)
freeRandomPoint world g | not $ elem point ((fruit world):(snake world)) =
(point, g1)
| otherwise = freeRandomPoint world g1 where
(point, g1) = randomPoint initWalls gГрафика
Перейдем к отображению мира. Базовая функция нашей графики drawPoint принимает символ и отображает его в заданной координате экрана. Функция renderWorld отображает наш мир. Без установленного флага isUpdateIteration, контроллеры moveController, collisionController и renderWorld не производят никаких изменений. Рендер отображает наш фрукт, новое положение змеи и затирает ее хвост. Стены отображаются один раз при старте и не обновляются.
renderWorld :: World -> IO ()
renderWorld world
| not $ isUpdateIteration world = return ()
| otherwise = do
drawPoint '@' (fruit world)
drawPoint ' ' (oldLast world)
mapM_ (drawPoint 'O') (snake world)
setCursorPosition 0 0
drawPoint :: Char -> Point -> IO ()
drawPoint char (x, y) = setCursorPosition y x >> putChar char
drawWalls :: Char -> Walls -> IO ()
drawWalls char ((x1, y1),(x2, y2)) = do
mapM_ (drawPoint char) [(x1, y)| y <- [y1..y2]]
mapM_ (drawPoint char) [(x, y1)| x <- [x1..x2]]
mapM_ (drawPoint char) [(x2, y)| y <- [y1..y2]]
mapM_ (drawPoint char) [(x, y2)| x <- [x1..x2]]
main = do
{-- … --}
drawWalls '#' initWalls
{-- … --}Подключаем все контроллеры и добавляем рендер в игровом цикле.
gameLoop inputThId input oldWorld = do
{-- … --}
let newWorld = collisionController . moveController $ timerController timePoint (inputController tryInput oldWorld)
renderWorld newWorld
{-- … --}На текущем этапе у нас есть рабочая змейка с контролем от пользователя. Добавим возможность игре проходить себя самостоятельно. Задачу идеального прохождения змейки очень подробно в своих видео разобрал австралийский кодер CodeBullet. Также об этом можно почитать у RussianDragon тут. Позаимствуем идею с циклом Гамильтона и приступим.
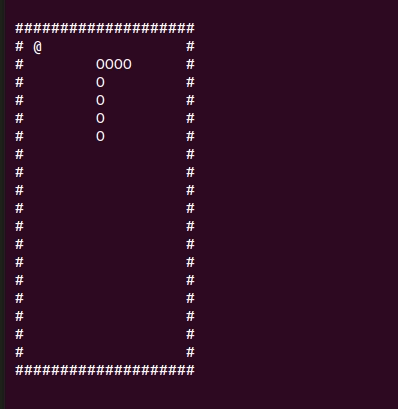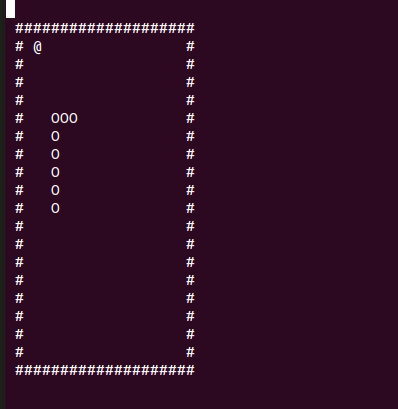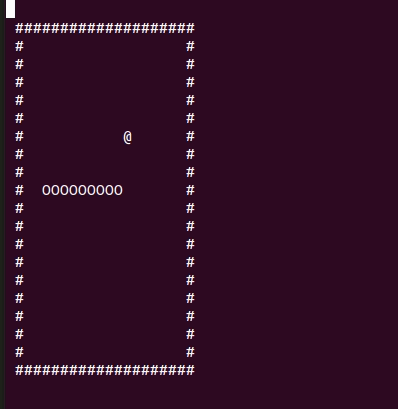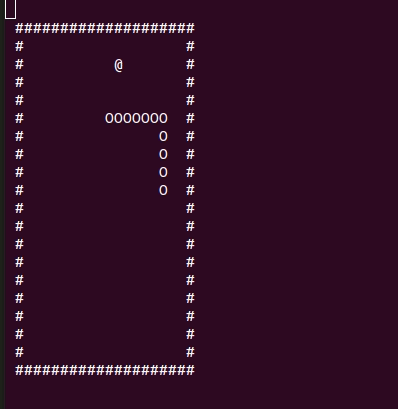
Цикл Гамильтона
Немного теории: цикл Гамильтона в контексте нашей игры — замкнутый путь, проходящий через каждую точку поля ровно один раз. Мы сможем его найти сделав проход по часовой стрелке. Добавим пару синонимов типов: Path — путь по игровому полю, ClosedPath — замкнутый путь или цикл Гамильтона для нашего поля.
type Path = [Point]
type ClosedPath = [Point]Напишем несколько вспомогательных функций, wallsFirstPoint вернет нулевую точку игрового поля внутри стен. С нее мы начнем составление цикла Гамильтона и соответственно в нее мы должны вернуться. isPathContain аналогично проверки столкновения змеи с телом, проверяет содержит ли путь точку. clockwise вернет список возможных направлений по часовой стрелке. distBetweenPoints — расстояние между двумя точками, учитывая что змея не может двигаться по диагонали.
clockwise = [DirUp, DirRight, DirDown, DirLeft]
wallsFirstPoint :: Point
wallsFirstPoint = ((fst $ fst initWalls) + 1, (snd $ fst initWalls) + 1)
isPathContain :: Path -> Point -> Bool
isPathContain path point = any (== point) path
distBetweenPoints :: Point -> Point -> Int
distBetweenPoints (x1, y1) (x2, y2) = abs (x1 - x2) + abs (y1 - y2)И сама функция поиска цикла Гамильтона getHamPath. Она принимает начальную точку цикла, второй аргумент является аккумулятором рекурсии, при вызове указываем пустой список. Функция проверяет, равна ли площадь нашего поля длине найденного пути Гамильтона и равно ли расстояние между первой и последней точкой пути единице, то есть пусть замкнулся и является циклом. Если нет, ищем следующую точку при помощи nextHamPathPoint. Даем ей текущий найденный путь и 4 возможных направления движения. Если точка не имеет коллизий со стеной и найденным путем, выбираем ее и включаем в путь. Вариант, что nextHamPathPoint не нашел ни одной точки крашит программу, так как цикл Гамильтона гарантированно должен быть найден. В нашем случае это может произойти только при условии, что у поля обе стороны четные и у пути нет возможности вернуться к начальной точке.
getHamPath :: Point -> ClosedPath -> ClosedPath
getHamPath currentPoint hamPath | hamPathCapacity initWalls == length (currentPoint:hamPath)
&& distBetweenPoints currentPoint (last hamPath) == 1
= currentPoint:hamPath
| otherwise = getHamPath newPoint (currentPoint:hamPath) where
newPoint = nextHamPathPoint (currentPoint:hamPath) clockwise
hamPathCapacity ((x1, y1),(x2, y2)) = (x2 - x1 - 1) * (y2 - y1 - 1)
nextHamPathPoint :: Path -> [StepDirection] -> Point
nextHamPathPoint _ [] = error "incorrect initWalls"
nextHamPathPoint hamPath (dir:dirs) | isPathContain hamPath virtualPoint
|| collisionWall virtualPoint initWalls =
nextHamPathPoint hamPath dirs
| otherwise = virtualPoint where
virtualPoint = pointStep dir (head hamPath)Добавим найденный цикл Гамильтона в наш мир.
data World = World {
{-- … --}
, hamPath :: ClosedPath
}
initWorld timePoint = World {
{-- … --}
, hamPath = getHamPath wallsFirstPoint []
} Внутри замкнутого пути наша змея может двигаться в 2х направлениях. Несмотря на то, что путь зациклен, он представляет из себя список с головой и хвостом. Будем считать движение от головы к хвосту DirFromHead и DirFromTail в обратном направлении.

data PathDirection = DirFromHead | DirFromTail deriving (Eq)Добавим к контроллеру движения змеи управление ботом при помощи функции nextDirOnPath, которую опишем позже. Она возвращает пару (botStepDir, botPathDir) первый элемент дает нам предложенное ботом направление змеи на поле. Второй указывает на движение внутри цикла Гамильтона. Если вернулось DirFromHead, то есть обратное текущему, переворачиваем цикл.
moveController world
{-- … --}
| worldState world == Process = world {snake = snakeStep (direction world) (snake world)}
| otherwise = world { snake = snakeStep botStepDir (snake world)
, hamPath = if botPathDir == DirFromTail then hamPath world else reverse $ hamPath world
} where
(botStepDir, botPathDir) = nextDirOnPath (snake world) (hamPath world)
nextDirOnPath :: Snake -> ClosedPath -> (StepDirection, PathDirection)
nextDirOnPath = undefinedДобавим пару вспомогательных функций: dirBetweenPoints вернет нам направление между двумя точками по меньшему расстоянию по оси и pointNeighborsOnPath вернет пару соседей точки внутри замкнутого пути.
dirBetweenPoints :: Point -> Point -> StepDirection
dirBetweenPoints (x1, y1) (x2, y2) | x1 == x2 = if y1 > y2 then DirUp else DirDown
| y1 == y2 = if x1 > x2 then DirLeft else DirRight
| otherwise = if abs (x1 - x2) < abs (y1 - y2) then
dirBetweenPoints (x1, 0) (x2, 0) else
dirBetweenPoints (0, y1) (0, y2)
pointNeighborsOnPath :: Point -> ClosedPath -> (Point, Point)
pointNeighborsOnPath point path | not $ isPathContain path point || length path < 4 = error "incorrect initWalls"
| point == head path = (last path, head $ tail path)
| point == last path = (last $ init path, head path)
| otherwise = _pointNeighborsOnPath point path where
_pointNeighborsOnPath point (a:b:c:xs) = if point == b then (a,c) else _pointNeighborsOnPath point (b:c:xs)Найдем на нашем замкнутом пути соседние точки для головы змеи, определим ту, которая является частью змеи и вернем направление к противоположному соседу.
nextDirOnPath :: Snake -> ClosedPath -> (StepDirection, PathDirection)
nextDirOnPath (snakeHead:snakeTail) path | snakeTail == [] = (dirBetweenPoints snakeHead point1, DirFromTail)
| point1 == head snakeTail = (dirBetweenPoints snakeHead point2, DirFromHead)
| otherwise = (dirBetweenPoints snakeHead point1, DirFromTail) where
(point1, point2) = pointNeighborsOnPath snakeHead pathСейчас у нас есть бот, который проходит змейку по найденному пути, не сокращая его.
Ускоряем бота
Попробуем ускорить бота, добавив еще пару функций: collisionSnakeOnPath проверит, свободен ли замкнутый путь начиная с точки в заданном направлении от тела змеи и distBetweenPointsOnPath которая вернет пару расстояний от точки до точки на замкнутом пути. Первый элемент будет расстоянием для DirFromTail направления, второй для DirFromHead.
collisionSnakeOnPath :: Snake -> Point -> ClosedPath -> PathDirection -> Bool
collisionSnakeOnPath snake point path pathDir | null $ common snake pathPart = False
| otherwise = True where
pathPart = takePathPart point (if pathDir == DirFromHead then path else reverse path) (length snake)
common xs ys = [ x | x <- xs , y <- ys, x == y]
takePathPart point path len = _takePathPart point (path ++ (take len path)) len where
_takePathPart _ [] _ = []
_takePathPart point (x:xs) len | x == point = x:(take (len - 1) xs)
| otherwise = _takePathPart point xs len
distBetweenPointsOnPath :: Point -> Point -> ClosedPath -> (Int, Int)
distBetweenPointsOnPath point1 point2 path | point1 == point2 = (0, 0)
| id1 < id2 = (length path - id2 + id1,id2 - id1)
| otherwise = (id1 - id2, length path - id1 + id2) where
(id1,id2) = pointIndexOnPath (point1,point2) path 0 (0,0)
pointIndexOnPath _ [] _ ids = ids
pointIndexOnPath (point1,point2) (x:xs) acc (id1,id2) | x == point1 = pointIndexOnPath (point1,point2) xs (acc+1) (acc,id2)
| x == point2 = pointIndexOnPath (point1,point2) xs (acc+1) (id1,acc)
| otherwise = pointIndexOnPath (point1,point2) xs (acc+1) (id1,id2) Сведем все в новую функцию управления змеей. Находим точку для сокращения цикла Гамильтона enterPointBypass в направлении фрукта, ищем самый короткий путь до фрукта в прямом и обратном направлении и проверяем ляжет ли туда змея. Если ничего не нашли, двигаемся дальше по циклу через nextDirOnPath.
nextDirBot :: Snake -> Point -> ClosedPath -> (StepDirection, PathDirection)
nextDirBot snake fruit path | distBypass1 < distBypass2 && distBypass1 < distToFruit1
&& not (collisionSnakeOnPath snake enterPointBypass path DirFromTail)
= (dirBetweenPoints (head snake) enterPointBypass, DirFromTail)
| distBypass2 < distToFruit1
&& not (collisionSnakeOnPath snake enterPointBypass path DirFromHead)
= (dirBetweenPoints (head snake) enterPointBypass, DirFromHead)
| otherwise = nextDirOnPath snake path where
dirBypass = dirBetweenPoints (head snake) fruit
enterPointBypass = pointStep dirBypass (head snake)
(distBypass1, distBypass2) = distBetweenPointsOnPath enterPointBypass fruit path
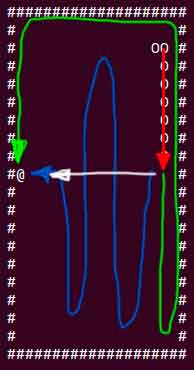
(distToFruit1, _) = distBetweenPointsOnPath (head snake) fruit pathПредложенный алгоритм сокращения пути не является оптимальным и имеет как минимум 2 явных проблемы. Мы рассматриваем точку входа для сокращения пути enterPointBypass только по направлению к фрукту, следовательно если цикл полностью заблокировал видимость фрукта, змея пойдет по полному пути. Также, если змея и фрукт расположены на достаточно большом расстоянии, как на картинке, бот выберет зеленое направление вместо белого, так как длину пути до фрукта мы сравниваем не по фактическому расстоянию на поле, а по длине цикла.
Подключим наш nextDirBot к контроллеру движения змеей, добавим меню и смотрим на результат.