Задачу о N ферзях признали NP-полной задачей
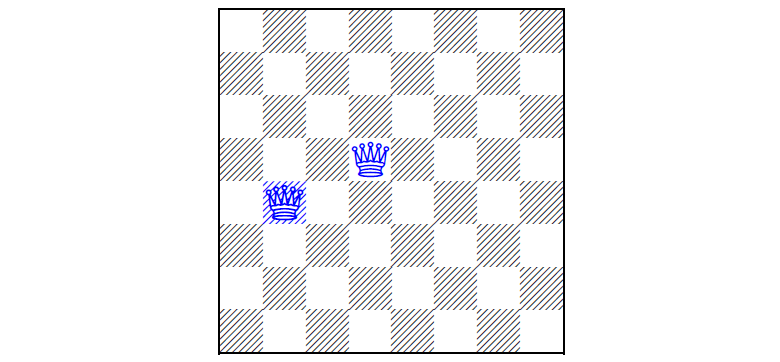
Первый вариант головоломки 1850 года, когда два ферзя заранее установлены на доску, а игрок должен расставить остальных ферзей (два решения задачи см. под катом)
Задача о N ферзях состоит в том, чтобы разместить N ферзей на доске размером N×N таким образом, чтобы ни один ферзь не находился под боем другого, при этом на доске заранее установлены несколько ферзей. То есть в итоге никакие два ферзя не должны находиться на одной линии или диагонали. Впервые задачку сформулировали в 1848 году, а в 1850 году придумали вариант головоломки, когда некоторое количество ферзей заранее поставлено на доску, а игрок должен расставить остальных, если это возможно.
Исследователи из Сент-Эндрюсского университета (Шотландия) опубликовали научную статью, в которой доказывают, что задача о N ферзях является не только #P-полной задачей, но также NP-полной задачей. Более того, Математический институт Клэя (США) готов заплатить миллион долларов любому, кто сможет оптимизировать решение этой задачи как задачи на доказательство P=NP.
Как известно, в теории сложности #P является классом проблем, решением которых является количество успешных, то есть, завершающихся в допускающих состояниях, путей вычислений для некой недетерминированной машины Тьюринга, работающей полиномиальное время. Класс #P принадлежит к классу NP и относится именно к вычислительным задачам среди задач разрешимости в классе NP.
Учёные отмечают, что эта задача может быть самой простой среди NP-полных задач, чтобы объяснить суть этих проблем любому человеку, который знает правила игры в шахматы. У этой задачи вообще очень интересная история. В своё время она привлекла внимание Гаусса, который даже сделал небольшую ошибку в её решении (на доске 8×8 он сообщил о 76 решениях, но потом сам признал четыре из них ошибочными, так что остались только 72).
Обобщение задачи для доски N×N привлекло внимание многих математиков. За последние полвека вышло несколько десятков научных работ, посвящённых этой проблеме. Как минимум шесть из них цитируются более 400 раз на Google Scholar: это Golomb & Baumert, 1965; Bitner & Reingold, 1975; Mackworth & Freuder, 1985; Minton, Johnston, Philips, & Laird, 1992; Selman, Levesque & Mitchell, 1992; Crawford, Ginsberg, Luks, & Roy, 1996.
Сложность задачи о N ферзях часто неправильно оценивают. Даже в обильно цитируемых работах её часто называют NP-сложной задачей (NP-hard), но она будет таковой только при условии, что P=NP. На самом деле вычислительный вариант задачи, то есть определение количества решений для N ферзей, представляет собой последовательность A000170 из Онлайн-энциклопедии целочисленных последовательностей. Эта последовательность сейчас известна максимум для n=27, где количество решений превышает 2,34×1017. Не известно ни одно более эффективное решение проблемы, чем простой перебор. Так, для n=27 в 2016 году использовался масштабный параллельный поиск на FPGA.
В то же время, если компьютер начнёт перебор возможных положений ферзей на доске 1000×1000 клеток, то он загрузится этой задачей навечно. По мнению учёных, если некто найдёт действительно быстрый и эффективный способ решения, то сможет извлечь из этого гораздо бóльшую выгоду, чем один миллион долларов от Математического института Клэя. «Если вы напишете программу, которая может решить проблему действительно быстро, вы могли бы адаптировать её для решения многих важных задач, с которыми мы сталкиваемся ежедневно, — говорит профессор информатики Ян Гент (Ian Gent), один из авторов научной работы. — Среди них тривиальные проблемы, такие как поиск самой большой группы ваших друзей в Facebook, которые не знают друг друга, или очень важные задачи, например, взлом кодов, которые обеспечивают безопасность всех наших онлайн-транзакций».
Но это чисто теоретические измышления. На практике никто пока не приблизился к решению задачи о N ферзях быстрым и эффективным способом. За доказательство, что существует более эффективный способ решения задачи, чем простой перебор всех вариантов, дадут миллион долларов.
Научная статья опубликована в августе 2017 года в журнале Journal of Artificial Intelligence Research (doi:10.1613/jair.5512, pdf).
P.S. Два решения задачи с КДПВ:

