Задача про обезьян и бесконечность13.04.2016 17:18

Всем известно, что если посадить обезьяну за печатную машинку и заставить ее вечно случайно стучать по клавишам, то, рано или поздно, она напечатает «Войну и мир», собрание трудов Пифагора и даже статью, которую вы сейчас читаете.

Потрясающий факт, но еще интереснее попытаться понять, сколько же времени ей понадобится для набора конкретного текста. А вам очевидно, что строку «abc» набирать гораздо быстрее чем «aaa»? Решению этой задачи и посвящен этот пост. Попутно объясняется префикс функция и ее свойства.

Понятно, что время, потраченное обезьяной на набор конкретного текста — это некоторая случайная величина. Поэтому логично спросить про ее математическое ожидание.

Формальная постановка задачи

Дана строка s, состоящая из прописных латинских букв («a»-«z»). Нужно найти мат. ожидание количества случайных нажатий на клавиши до того, как будет набрана вся строка s, если все символы набираются равновероятно (с вероятностью 1/26).

Код решения

Чтобы понять, почему это работает и что это за функция Pi () нужно прочитать всю статью :(.

string s; //строка, которую набирает обезьяна
int n = s.length();
vector p = Pi(s);
vector pow(n+1);
pow[0] = 1;
int i;
for (i = 1; i <= n; i++) {
  pow[i] = pow[i-1]*26;
}
long double ans = 0;
for (i = n; i>0; i = p[i-1]) {
  ans += pow[i];
}
cout << ans;

Префикс функция

Именно эта функция поможет нам решить поставленную задачу. Префикс функция была введена Д. Кнутом и М. Праттом (и параллельно Д. Моррисом) для их знаменитого алгоритма поиска подстроки в строке (алгоритм КМП). Префикс функция для строки s возвращает длину самого длинного собственного префикса строки, который также является ее суффиксом.

Префиксы и суффиксы

Префикс — это просто начало строки, если отбросить сколько-то символов с конца. Так у строки «aba» есть 4 префикса:» (пустая строка), «a», «ab» и «aba». Суффикс — тоже самое, но символы удаляются с начала. При этом некоторые суффиксы и префиксы могут совпасть. Для строки «aba» есть 3 таких префикса-суффикса:», «a» и «aba» (четвертый суффикс «ba» не совпадает с префиксом «ab»). Суффикс или префикс называется собственным, если он короче всей строки.

Формально говоря: $\pi(s) = max\{ k \,|\, 0\le k < |s|,\, pref_k(s) = suf_k(s)\}$

Где prefk (s) — это префикс длины k строки s, а sufk (s) — это суффикс длины k строки s.

Как в алгоритме КМП, так и в других применениях, гораздо полезнее рассматривать префикс функцию сразу для всех префиксов данной строки. Да, звучит страшно — для каждого префикса нужно найти наибольший собственный префикс, который совпадает с суффиксом префикса. Но на самом деле все просто:

$\pi_s(k) = \pi(pref_k(s)),\, 1\le k \le |s|$

Такая расширенная префикс функция полезна прежде всего тем, что ее проще вычислять, чем просто $\pi(s)$ . Ниже показаны значения $\pi_s(k)$ для s=«ababac».

   k: 1 2 3 4 5 6
   s: a b a b a c
P(i): 0 0 1 2 3 0

Вычисление префикс функции

Код вычисления

vector Pi(string s) {
  int n = s.length();
  vector p(n);
  p[0] = 0;
  for (int i = 1; i < n; i++) {
    int j = p[i-1]; 
    while (j > 0 && s[i] != s[j]) { 
      j = p[j];
    }
    if (s[i] == s[j]) j++;
    p[i] = j;
  } 
  return p;
}

Быстрое, за O (N), вычисление префикс функции основано на двух простых наблюдениях.

(1) Чтобы получить префикс-суффикс для позиции k надо взять какой-то префикс-суффикс для позиции k-1 и дописать к нему в конец символ на позиции k.

(2) Все префиксы-суффиксы строки s длины n можно получить как $\pi_s(n),\, \pi_s(\pi_s(n)),\, \pi_s(\pi_s(\pi_s(n)))$ и так далее, пока очередное значение не станет равным 0. Это свойство можно проверить на строке «abacaba». Тут $\pi_s(7)=3,\, \pi_s(3)=1,\, \pi_s(1)=0$ , что соответствует всем префиксам-суффиксам («aba», «a» и »). Так получается потому, что максимальный префикс-суффикс имеет длину $\pi_s(n)$ . Следующий по длине префикс-суффикс будет короче. Но поскольку первый префикс-суффикс встречается как в начале, так и на конце строки s, то следующий префифкс-суффикс будет длиннейшим префиксом-суффиксом в первом префиксе-суффиксе.

Поэтому для построения префикс функции для позиции i достаточно проитерироваться начиная со значения префикс функции в предыдущей позиции пока продолжение суффикса новым символом не будет также и префиксом (для этого надо проверить только один новый символ). Такой алгоритм выполняется за линейное время, потому что значение префикс функции каждый раз увеличивается максимум на 1, поэтому оно не может уменьшится более чем n раз, а значит, вложенный цикл суммарно выполнится не более чем n раз.

Конечный автомат KMP

Следующий математический объект, необходимый в решении поставленной задачи — это конечный автомат, принимающий строки, заканчивающиеся на заданную строку s. Этот автомат используется в другой, менее известной модификации алгоритма Кнута-Морисса-Пратта. В этой версии алгоритма строится конечный автомат, который принимает все строки, которые заканчиваются на заданную строку (шаблон). Затем автомату передается строка-текст. Каждый раз, когда автомат принимает переданный ему текст, найдено очередное вхождение шаблона. Именно этот автомат и поможет нам решить задачу об обезьяне за печатоной машинкой.

Что такое конечный автомат

Конечный автомат — это математический объект который проще всего представить себе как некоторую коробку у которой есть какое-то внутреннее состояние. Изначально коробка находится в начальном состоянии. В коробку можно вводить строки, по одному символу за раз. После каждого символа коробка меняет свое состояние, при чем в зависимости от текущего состояния и введенного символа. Так же некоторые состояния являются хорошими (математический термин — конечные состояния). Говорят, что автомат принимает строку, если после скармливания ему этой строки символ-за-символом, автомат находится в хорошем состоянии.

Для определения КА нужно определить начальное состояние, хорошие состояния и функцию перехода — для каждого состояния и символа нужно указать новое состояние, в которое автомат перейдет. Удобно рисовать автомат как полный ориентированный граф, где вершины — это стостояния, а на каждом ребре написан ровно один символ. Из каждой вершины должно быть ровно одно ребро с каждым символом. Тогда для обработки какой-то строки надо просто перейти по ребрам с символами из этой строки. Если путь закончился в конечном состоянии, то автомат такую строку принимает.

Для построения этого автомата мы будем использовать уже известную нам префикс функцию.
В автомате будет n+1 состояние, пронумерованные от 0 до n. Состояние k соответствует совпадению последних k набранных символов с префиксом шаблона длины k (Если мы ищем строку «abac» то нам от текущего текста интересно только что там на конце: «abac», «aba», «ab», «a» или что-то друге. Этой информации достаточно чтоб получить такуюже после дописывания одного символа). Состояние 0 будет начальным, а состояние n — конечным. Иногда может быть неразбериха: например, для сроки «ababccc» при скормленой автамату строке «zzzabab» можно выбрать как состояние 2, так и 4. Но, чтобы не терять нужную информацию о набранном тексте, мы всегда будем выбирать наибольшее состояние.

пример конечного автомата KMP

Вот автомат для строки «ababac». Для примера алфавит состоит только из символов 'a'-'c'. Параллельные ребра объединены для наглядности. На самом деле каждому ребру соответствует только один символ. Начальное состояние — 0, конечное — 6.

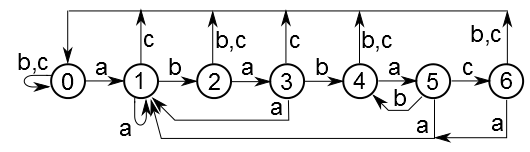
Несложно убедиться, что любой путь из состояния 0 в состояние 6, каким бы сложным он не был, обязательно кончается на строку «ababac». И наоборот, любой такой путь обязательно закончится в состоянии 6.

Код построения конечного автомата

string s; //исходная строка.
int n = s.length();
vector< vector > nxt(n+1, vector(256)); 
// функция перехода nxt[состояние][символ] == новое состояние
vector p = Pi(s); // Префикс функция. См. код выше
nxt[0][s[0]] = 1; //единственный переход из состояния 0 не в 0.
for (int i = 1; i <= n; i++) {
  for (int c = 0; c < 256; c++)
    nxt[i][c] = nxt[p[i-1]][c]; //p[] индексируется с нуля, поэтому нужно -1
  if (i < n) nxt[i][s[i]] = i+1;
}

Обратите внимание, как строятся переходы. Для расчета переходов из состояния i мы рассматриваем 2 варианта. Если новый символ — это s[i] — то переход будет в состояние i+1. Тут все очевидно: если было совпадение в i символов — то добавив следующий символ из строки s мы увеличим длину совпадения на 1. Если же символ не совпал, то мы просто копируем переходы из состояния $\pi_s(i)$ . Почему? Переход в этом случае будет точно в состояние с номером ≤i. Значит после перехода мы забудем часть информации о набранном тексте. Можно сделать это перед переходом. Самый минимум, что мы можем стереть, это притвориться что на самом деле сейчас состояние не i, а $\pi_s(i)$ . Это как в том примере выше, можно было считать что текст кончается на «abab» или «ab». Если из «abab» никаких переходов нет — можно использовать переходы из «ab».

Решение

Теперь мы готовы решить поставленную задачу.
Построим для строки s автомат KMP. Поскольку все символы набираются обезьяной случайно, нам не важны сами символы, а только ребра в графе переходов. Задачу можно переформулировать так: найти мат. ожидание количества переходов в случайном блуждании из состояния 0 пока не достигнуто состояние n.

Логично в такой постановке ввести переменные: Ek, 0≤k≤n — матожидание количества переходов до достижения состояния n. E0 будет ответом к исходной задаче. Пусть Z — это множество допустимых символов (алфавит). Можно составить систему уравнений:

$(1)$

$E_n = 0$

$(2)$

$E_k = 1 + \frac{1}{|Z|}\sum_{c \in Z}{E_{nxt[k][c]}}, k=0..n-1$

Уравнение (1) означает, что достигнув состояния n случайное блуждание останавливается.
Для любого другого состояния будет сделан какой-то переход, поэтому в уравнении (2) присутствует слагаемое 1. Второе слагаемое — это сумма по всем возможным вариантам, умноженным на вероятность этих вариантов. Все вероятности одинаковы — поэтому она вынесена за знак суммы.

Вот уже есть решение задачи за O (n^3): построенную систему линейных уравнений можно решить методом Гаусса. Но если немного посмотреть на эту систему и вспомнить, что есть префикс функция, то есть решение гораздо проще и быстрее.

Вспомним построение конечного автомата. (Для простоты далее вместо $\pi_s$ я буду использовать просто $\pi$ ). Переходы из состояния k почти полностью совпадают с переходами из состояния $\pi(k)$ . Отличие в переходе только по символу s[k-1]. Поэтому правые части уравнений (2) для состояний k и $\pi(k)$ отличаются только одним слагаемым. В уравнении для $\pi(k)$ стоит $E_{nxt[\pi(k)][s[k-1]]}$ вместо $E_{nxt[k][s[k-1]]}$ в уравнении для k. При чем nxt[k][s[k-1]]=k+1. Используя этот факт можно переписать уравнения (2):

$(3)$

$E_k = E_{\pi(k)} + \frac{1}{|Z|}(E_{k+1}-E_{nxt[\pi(k)][s[k-1]]})$

Теперь нужно сделать еще одно наблюдение. Оказывается

$nxt[\pi(k)[s[k-1]] = \pi(k+1)$

Т.е. чтобы найти префикс функцию для какого-то состояния, надо взять префикс функцию от предыдущего состояния и перейти оттуда по символу, ведущему в следующее состояние.
Действительно, если рассмотреть состояние $\pi(k)$ , то оно соответствует строке, заканчивающейся на символ s[k-1]. Значит туда есть переходы по этому символу. Рассмотрим самое большое состояние, из которого такой переход есть, но которое имеет номер < k. Если после перехода по символу s[k-1] мы получили какой-то суффикс $pref_k(s)$ , то до перехода это был суффикс $pref_{k-1}(s)$ . Поскольку это было самое правое такое состояние, то оно соответствует максимальному префиксу-суффиксу $pref_{k-1}(s)$ , а значит оно имеет номер $\pi(k-1)$ . Вот мы и получили этот удивительный и полезный факт.

Тогда (3) преобразуется в:

$E_k = E_{\pi(k)} + \frac{1}{|Z|}(E_{k+1}-E_{\pi(k+1)})$

Или по-другому:

$|Z| (E_k - E_{\pi(k)}) =(E_{k+1}-E_{\pi(k+1)})$

С обеих сторон от знака равенства тут отрицательные числа (логично, что чем больше k, тем меньше Ek). Умножим обе части на -1.

$(4)$

$|Z| (E_{\pi(k)}-E_k) =E_{\pi(k+1)}-E_{k+1}$

Но (4) справедливо только для k>0. Для k=0 можно явно выписать уравнение (2), ведь только один из |Z| переходов ведет в состояние 1, а все остальные возвращаются в состояние 0:

$E_0 = 1 + \frac{1}{|Z|}E_1 + \frac{|Z|-1}{|Z|}E_0$

Теперь соберем все переменные слева, домножим уравнение на |Z| и заменим $0=\pi(1)$ (префикс функция для одного символа всегда равна 0, т.к. непустых собственных префиксов у одного символа нет):

$(5)$

$E_{\pi(1)} - E_1 = |Z|$

Я позволю себе повторить уравнения (1), (4) и (5), так как они составляют систему, которую мы теперь решим аналитически:

$E_{\pi(1)} - E_1 = |Z| \ |Z| (E_{\pi(k)}-E_k) =E_{\pi(k+1)}-E_{k+1},\, k=1..n-1 \ E_n = 0$

Подставляя первое уравнение в левую часть второго при k=1, затем при k=2 и т.д. получаем:

$(6)$

$E_{\pi(k)} - E_k = |Z|^k ,\, k=1..n$

Вот уже решение почти готово: теперь рассмотрим (6) при k=n и вспомним, что $E_n = 0$ , получаем:

$E_{\pi(n)} = |Z|^n$

Подставляем это значение в (6) при $k = \pi(n)$ — получаем:

$E_{\pi(\pi(n))} = |Z|^n + |Z|^{\pi(n)}$

Аналогично, получаем:

$E_{\pi(\pi(\pi(n)))} = |Z|^n + |Z|^{\pi(n)} + |Z|^{\pi(\pi(n))}$

И так можно продолжать то тех пор, пока не получим выражение для $E_0$ , что, кстати, и является ответом к задаче. Обозначим $\pi^k$ примененную k раз подряд функцию $\pi$ , тогда:

$(*)$

$E_0 = \sum_{k:\pi^k(n) > 0}|Z|^k$

Таким образом, мы получили решение задачи за O (n): построить префикс функцию к строке s и итерироваться по ней начиная с n пока не достигнем 0, попутно складывая степени |Z| равные текущей длине префикса. Это и есть то самое решение, приведенное в начале статьи.

Глядя на (*) становится понятно, почему строку «aaa» набрать сложнее чем «abc», ведь в у «aaa» только третья итерация $\pi$ равна нулю, а у второй строки вообще нет непустых префиксов равным суффиксам и $\pi$ сразу дает ноль.

Замечания

Префикс функция и автомат КМП очень полезные инструменты для работы со строками. Если у уважаемых читателей есть интерес, то я могу разобрать решения других задач. О любых опечатках прошу сообщать в личку, спасибо.