Задача о форме поверхности вращающейся жидкости
Размешивая утром сахар в чае или кофе, можно заметить, что форма поверхности воды в стакане принимает форму воронки. О том, какая эта форма люди задумывались давно, например, на Хабре есть статья https://habr.com/ru/post/345994, где утверждается, что это параболоид (парабола, если смотреть в разрезе). Однако, легко убедиться в том, что на самом деле это не совсем парабола. Вернее, совсем не парабола. А что же это тогда ?
Для того, чтобы вычислить, какую форму приобретёт вода (ну или другая жидкость) в стакане, необходимо учитывать вязкость и влияние стенок стакана. Поэтому здесь надо использовать уравнения Навье-Стокса для вязкой несжимаемой жидкости. Поскольку стакан имеет цилиндрическую форму, то и уравнения Навье-Стокса надо записать в цилиндрических координатах, где ось z идет по центру стакана и направлена вверх, а r — расстояние от этой оси. В общем виде уравнения Навье-Стокса в цилиндрических координатах выглядят следующим образом (Ландау-Лифшиц Гидродинамика):
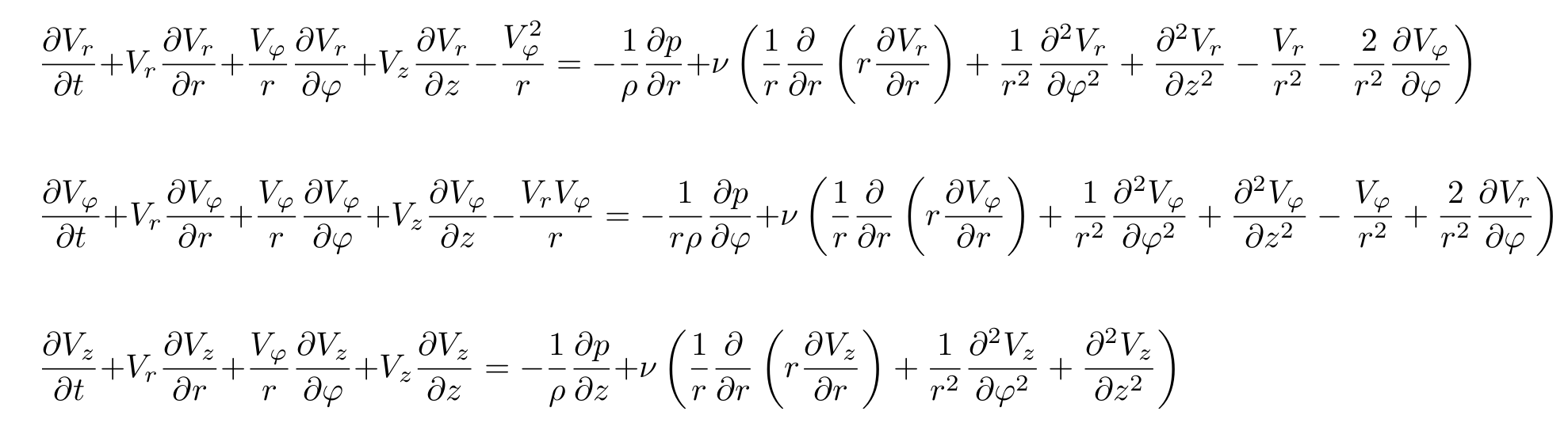
Здесь ро — плотность жидкости, а ню — кинематическая вязкость.
Решить такую систему уравнений в аналитическом виде представляет большую сложность, поэтому мы сделаем два разумных упрощения. Первое, будем считать, что дно стакана не воздействует на форму жидкости, т.е. стакан достаточно глубокий. Второе — будем считать, что скорость вращения жидкости по окружности значительно больше, чем скорость перемещения жидкости вверх-вниз и от центра стакана к и от его стенок. Т.е. этими скоростями можно пренебречь. С учетом таких упрощений, третье уравнение нашей системы превратится в тождество, а оставшиеся два будут выглядеть следующим образом:
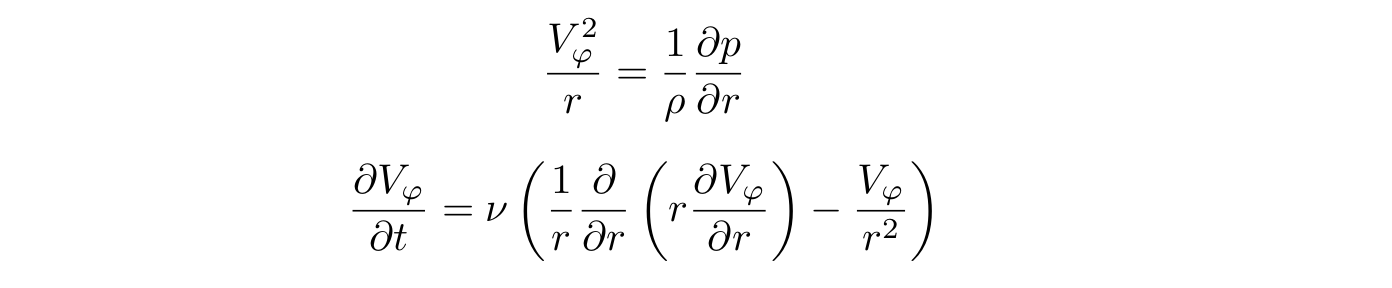
Давление внутри жидкости в любой точке прямо пропорционально столбу жидкости над этой точкой и вычисляется по известной формуле:
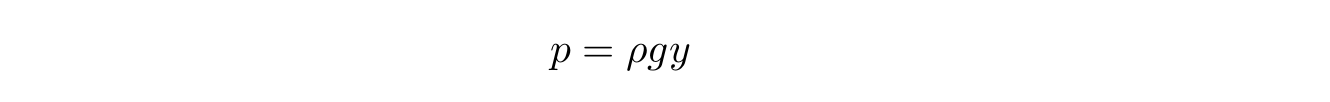
где g — ускорение свободного падения, а y — высота столба жидкости для фиксированного z, которая, собственно, и задаёт форму поверхности. Таким образом, первое уравнение можно переписать в следующем виде:
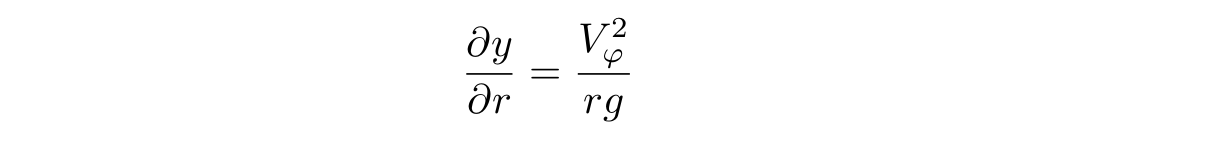
Надо заметить, что если угловая скорость omega постоянна, то можно получить пресловутую параболу, поскольку:
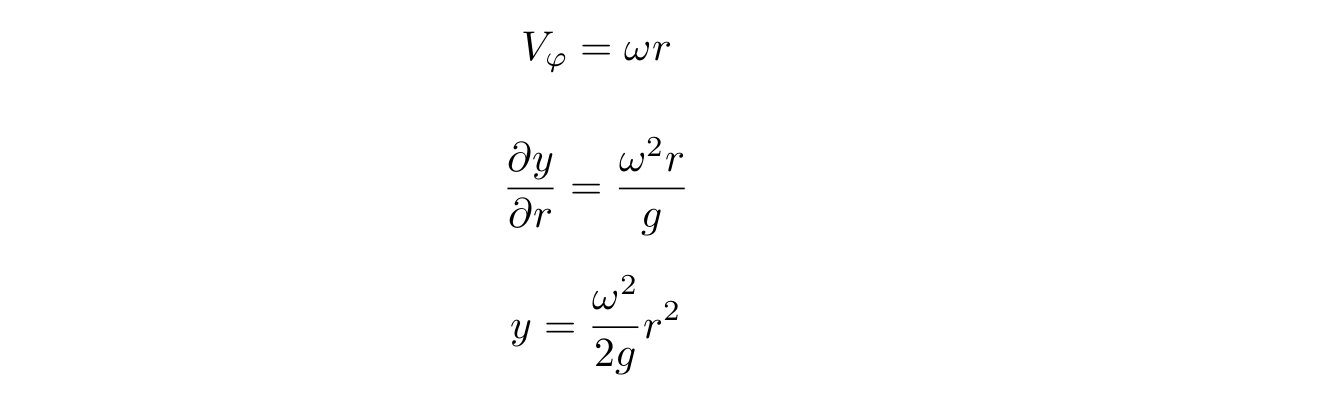
Однако, в нашем случае касательная скорость зависит от расстояния до стенок, поскольку, согласно гидродинамике, скорость около стенок равна нулю. Значение этой скорости получим из второго уравнения:

Касательная скорость зависит не только от расстояния до стенок стакана, но и от времени, поскольку жидкость вязкая, энергия вращения теряется на трение. Для того, чтобы решить второе уравнение, представим касательную скорость в виде произведения двух функций, одна из которых зависит только от расстояния от оси стакана, а вторая только от времени:
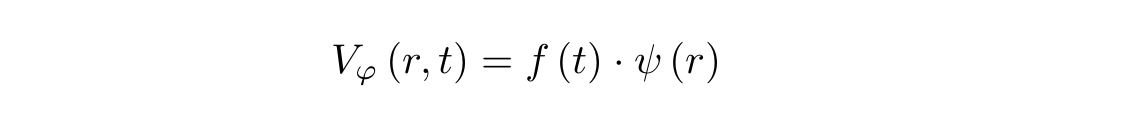
Подставив во второе уравнение, получим:
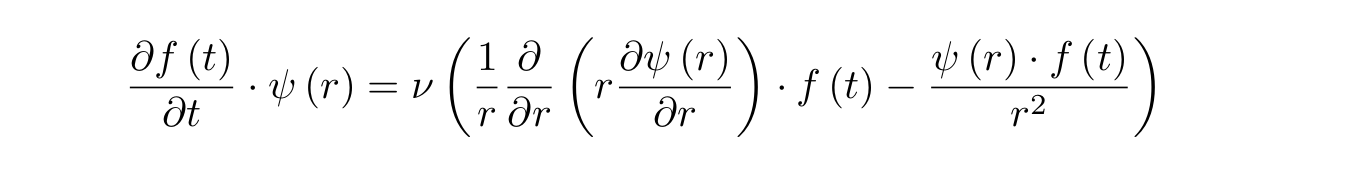
Если разделить это уравнение на саму функцию и ню, то легко увидеть, что первая часть равенства зависит только от времени, а вторая только
от r. Значит, их можно приравнять некоторой константе лямбда:

Решим сначала уравнение для той части, которая зависит от расстояния от центра стакана r:

Продифференцируем выражение в скобках:
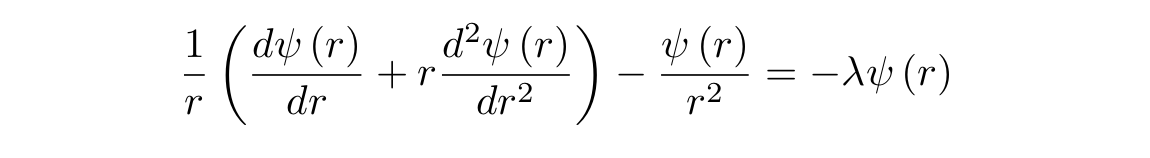
Раскроем скобку:
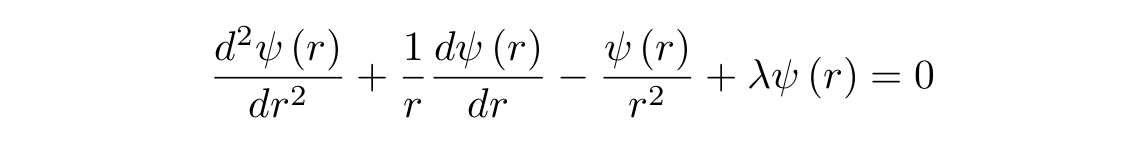
Сгруппируем и умножим на r в квадрате:
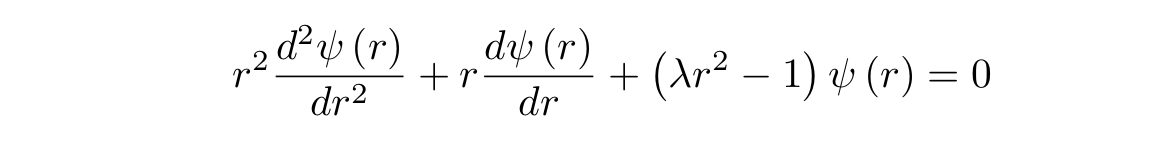
Получилось красивое дифференциальное уравнение, но мешает лямбда. Чтобы от нее избавиться, сделаем замену переменной:
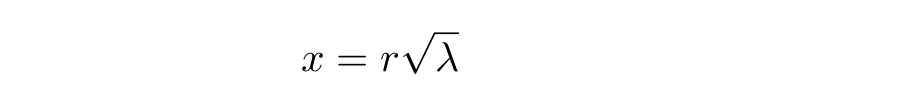
Тогда:
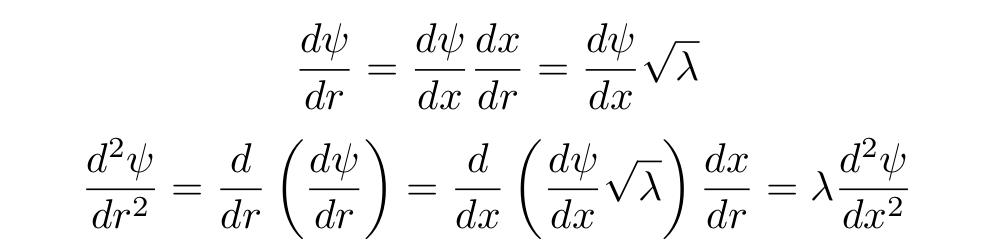
И наше уравнение принимает вид:
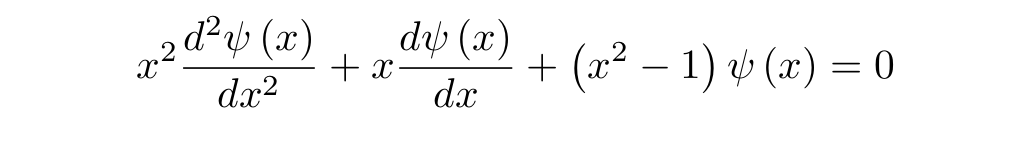
Это уравнение Бесселя первого порядка. Для того, чтобы точно узнать распределение касательной скорости, надо воспользоваться граничным условием, гласящим, что у стенки стакана скорость будет равна нулю, то есть это будет первый нуль функции Бесселя первого порядка равный:

Из этого условия можно найти значение лямбда. Поскольку

где R — радиус стакана, можно найти
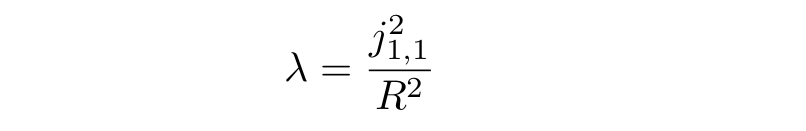
Таким образом, распределение касательной скорости от расстояния от центра стакана будет выглядеть следующим образом:
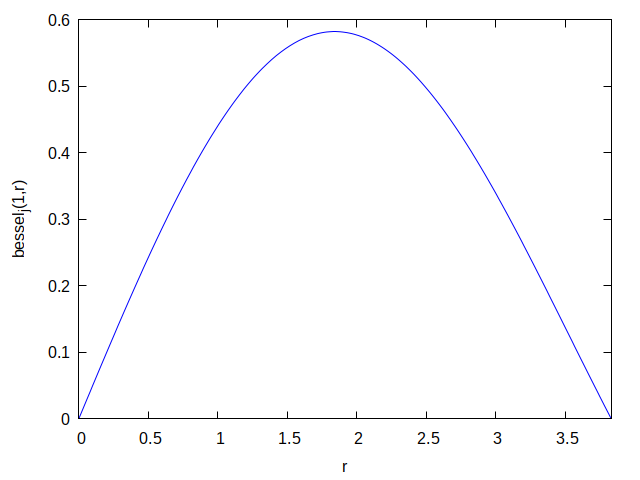
Для того, чтобы найти зависимость касательной скорости от времени, подставим найденное значение лямбда в ту часть, которая зависит только от времени:
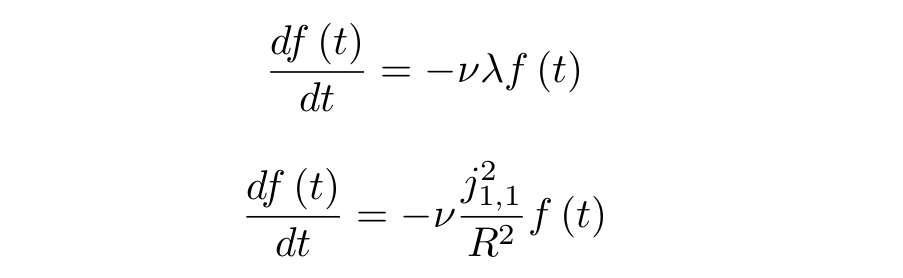
Решив это уравнение, получим:
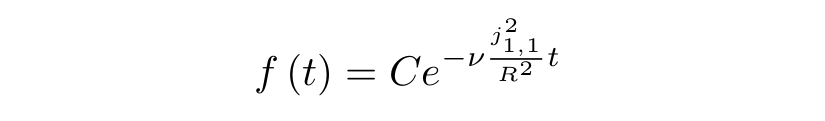
где C — константа. Можно подсчитать, за какое время касательная скорость уменьшается в два раза:
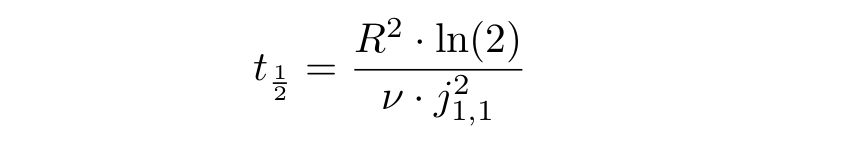
Окончательно зависимость касательной скорости от расстояния и времени будет:
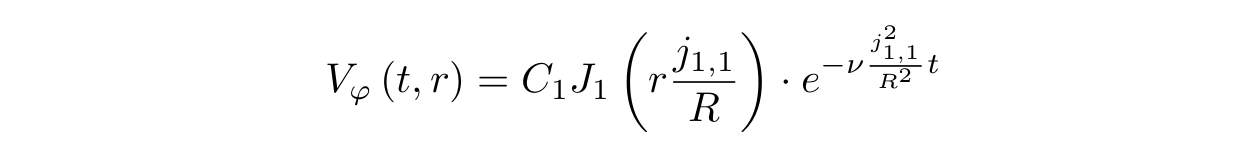
Найдем теперь, собственно, форму поверхности. Для этого подставим значение касательной скорости в уравнение для y:
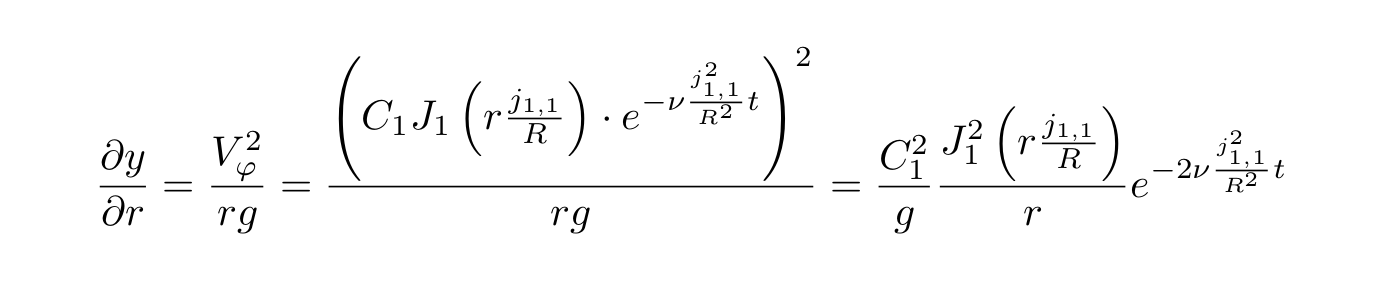
Интегрируем и получаем:

Здесь C1 и C2 — константы, зависящие от того, насколько сильно мы раскрутили жидкость и от глубины нашего стакана. Профиль нашей вращающейся жидкости будет выглядеть следующим образом:
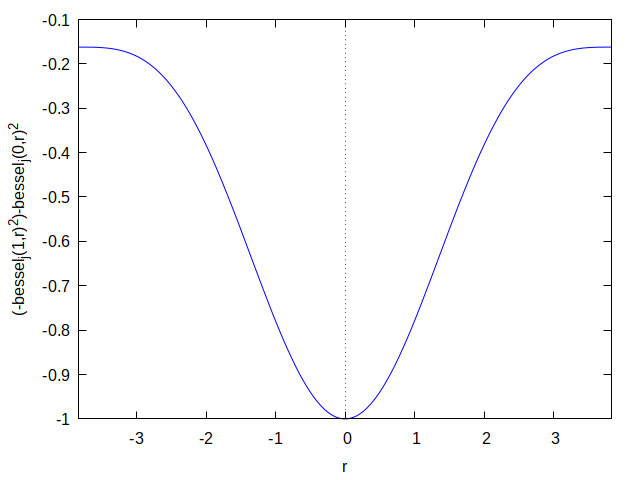
А если его представить в 3d, то вот так:

Похоже ли это на реальную форму чая у вас утром, пишите в комментариях.
