Взлом квантовой программы12.07.2021 16:16

Программы для квантового компьютера тоже могут содержать уязвимости. Эти уязвимости могут позволять удалённо выполнять какие-то вычисления.
Как же написать шеллкод для программы, уязвимой к исполнению квантового кода?

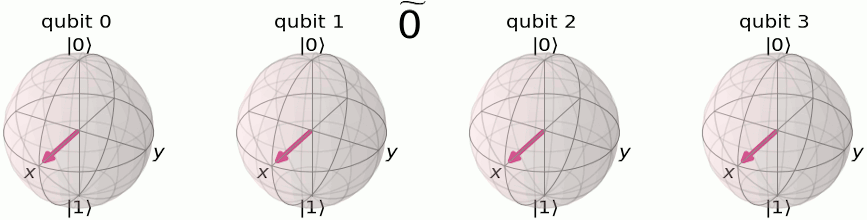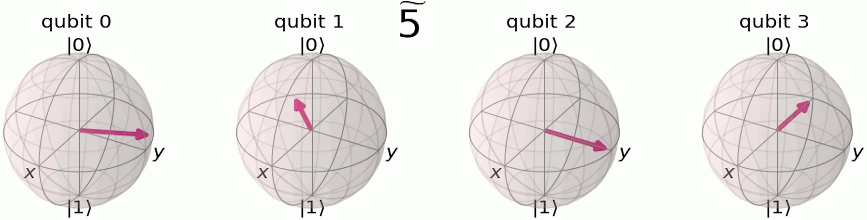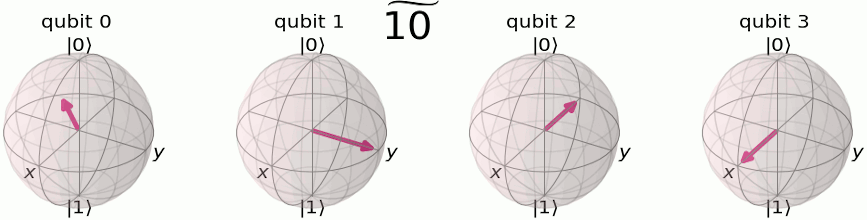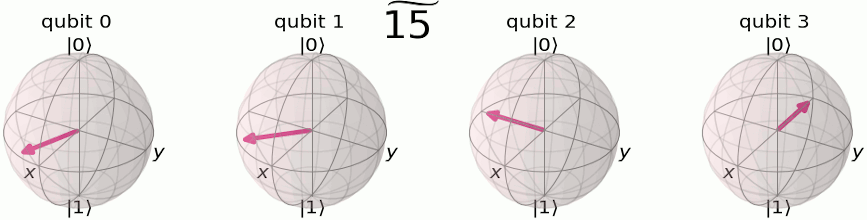
aixm4tecgfmlruxm2cimaqnyrnu.gif

Привет читателям блога компании DeteAct!
Меня зовут Омар Ганиев, многие меня знают по нику «Beched».

Мы занимаемся пентестами и аудитами безопасности и любим решать сложные задачи, в том числе в свободное время. При этом приходится следить за передовыми технологиями, поэтому хочу немного рассказать про «квантовый шеллкодинг» на примере одной задачки из недавнего хакквеста.
Спасибо автору задачи Владимиру keltecc, который, кстати, уже выложил исходники задания на гитхабе.

Квантовое программирование — это тоже программирование, и в квантовых программах тоже могут быть уязвимости. Автор задачи создал сервис, который симулирует некоторые квантовые вычисления с использованием секретного значения («флага») и пользовательского ввода.

В решении задачи есть две части: реверс-инжиниринг логики .NET-приложения на Q# и собственно программирование квантового эксплойта.

Реверс-инжинирим


Нам даны скомпилированные файлы проекта в виде нескольких DLL на Q# и ELF-файл сервиса. Исходников нет.
Вооружившись инструментами dotPeek и dnSpy, принимаемся декомпилировать DLL и изучать логику приложения.

3vd2fj0qymbfnfhf1lnptevkfnm.png
Эти инструменты, конечно, не умеют декомпилировать .NET-байткод в Q#-код, поэтому мы получаем лишь C#-код, причём с некоторыми потерями. Каждый из инструментов не справляется с декомпиляцией некоторых кусков кода, но суммарно картина видна.
Так, при помощи dotPeek разбираемся с точкой входа в ZN.Runner.dll:

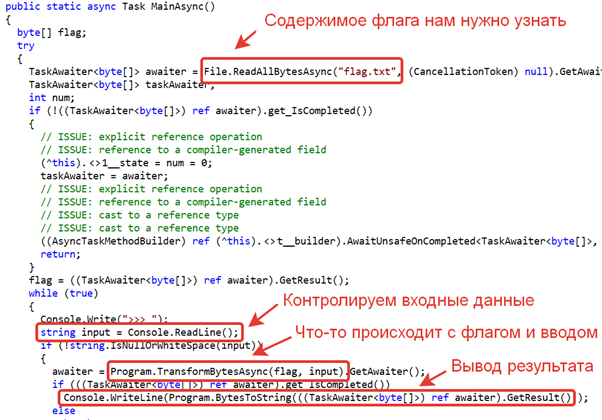
dr3tio72thi7biwofqk7khvasxs.png

Тут можно разобрать, что программа считывает флаг из файла, далее считывает строку, переданную пользователем, затем производит какое-то преобразование над этими буферами и выдаёт результат.
Открываем код процедуры Program.TransformBytesAsync, которая производит интересующее нас преобразование:

vcb86dpta3pbmbk7ejzynbdvaue.png

Итак, всё выглядит довольно непонятно, но, не обращая внимание на преобразования типов, мы можем понять, что по всей видимости флаг и наша строка попадают в квантовый симулятор, и сами вычисления реализованы в классе TransformBytes, который можно найти в файле ZN.Quantum.dll.

Здесь нам перестаёт помогать dotPeek, и приходится обратиться к dnSpy. Низкоуровневый класс TransformBytes, который мы видим в декомпиляторе, соответствует такой штуке, как операция (operation) в Q#. Тело операции имплементировано в методе __Body__ декомпилированного класса:

tybke1k1_5zkiop8mgyqnpelqri.png

По декомпилированному коду видно, что поочерёдно для каждого байта флага производятся следующие операции:

  1. Инициализируется массив iqarray из 8 кубитов,
  2. При помощи ConstructOperations создаётся массив унитарных преобразований (тип IUnitary) iqarray2,
  3. Применяется NumberToBigEndian к байту флага, результат записывается в iqarray,
  4. К iqarray применяется Microsoft.Quantum.Canon.QFT,
  5. К первому кубиту (iqarray[0]) применяются операции из массива iqarray2 при помощи ApplyOperations.

Операция ConstructOperations формирует массив (последовательность) квантовых гейтов в зависимости от строк, считанных из ввода через CycleStringReader:

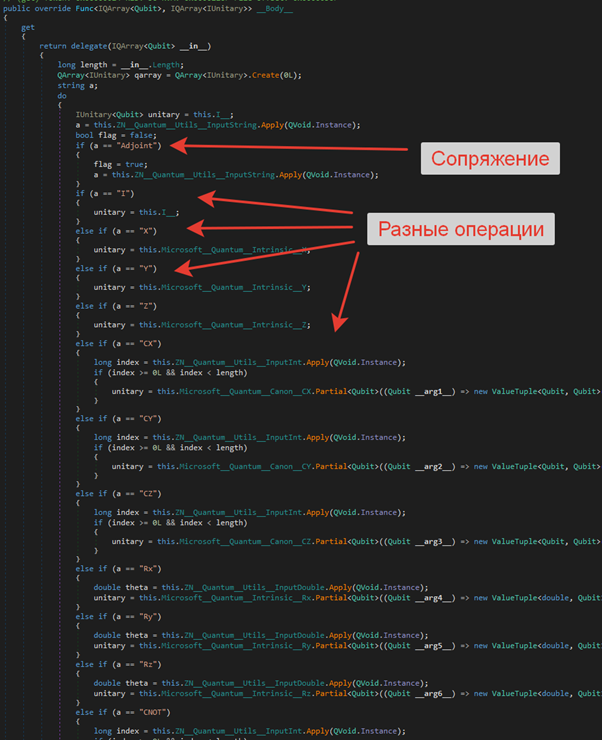
wzsyr9dd9ogrvv75i4wflt16yiu.png

Для исполнения доступны следующие операции, которые будут применены к первому кубиту из нашего массива:

  • Adjoint (сопряжение)
  • I (тождественная операция)
  • X, Y, Z
  • CX, CY, CZ
  • Rx, Ry, Rz
  • CNOT
  • SWAP (можно поменять местами первый кубит с i-м)

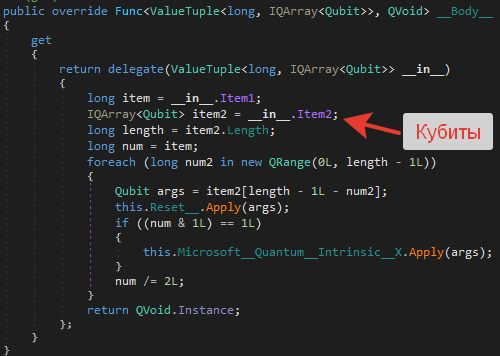
Операция NumberToBigEndian «намазывает» классические биты целочисленного аргумента на массив кубитов, так что изначально каждый кубит равен 0 или 1:

g1ja3wpd3rmt5qshtrbzinplwag.png

Следом применяется операция QFT, т.е. квантовое преобразование Фурье. Именно это преобразование делает вывод программы случайным набором битов вместо битов флага.
В итоге выполняется операция ApplyOperations, которая просто берёт массив гейтов, полученный при помощи ConstructOperations, и последовательно применяет их после QFT.

Суть задачи


Таким образом, мы разобрались, что программа считывает флаг, «рандомизирует» его при помощи QFT, после чего исполняет контролируемый нами квантовый код из ограниченного множества гейтов.
По сути программа уязвима к удалённому исполнению (почти) произвольного кода в квантовой машине. Это то, что обычно называется RCE.

Наша задача — написать эксплойт для этой уязвимости, составив из доступных нам гейтов такой код, что мы сможем обратить действие QFT.
Отправив этот набор гейтов на сервер, в ответ мы детерминированно получим изначальное значение флага!

Пишем квантовый эксплойт


Применение квантовой операции — суть умножение на матрицу. Квантовое преобразование Фурье — это перемножение некоторого количества матриц. Преобразование может быть применено к серии кубитов, в нашем случае это массив из 8 кубитов.
На картинке ниже из Википедии схематично показана работа QFT для n кубитов:

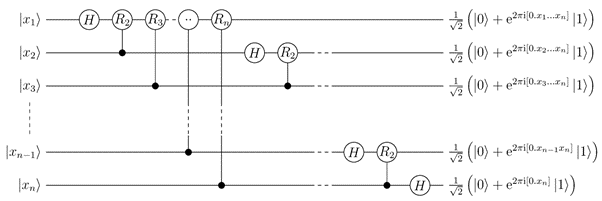
nqoro8pm7elltzybawhtyxmzz8i.png

Здесь H — это гейт Адамара, замечательное преобразование, в результате которого кубит при измерении будет равновероятно возвращать 0 или 1. Матрица этого оператора выглядит следующим образом:

q2eclcdtsxsvbgghf_n9d9w-qss.png

Rk — это контролируемые версии фазовых вращений, матрица которых для 2 кубитов выглядит так:

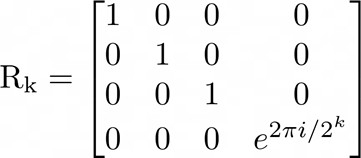
frspkknqmmzzdsmzlj7crocqcom.png

Для того, чтобы построить обратное преобразование, нам нужно выполнить операции в обратном порядке, при этом вместо каждой матрицы брать эрмитово-сопряжённую ей (поскольку все преобразования унитарны).

Но вот незадача: у нас в наборе гейтов, доступных в ConstructOperations, нет ни H, ни Rk, ни сопряжённых им операторов (кстати, оператор Адамара сопряжён сам себе).
Значит, нам надо как-то выразить эти операторы через доступные нам. Оказывается, гейт Адамара мы можем выразить, например, через операторы Z и Ry (pi/2), что легко проверить, перемножив соответствующие матрицы.

С контролируемыми вращениями сложнее: листая документацию Q# по доступным операторам можно заметить, что самая похожая матрица у оператора Rz. На самом деле, это как раз то, что нам нужно, поскольку Rz с подходящим аргументом отличается от Rk только в глобальной фазе, что не влияет на результат вычислений.

Вот только кое-чего нам не хватает в Rz: контролируемости. Её мы можем достичь при помощи такой хитрости: если нам нужно выполнить контролируемое вращение Rz (theta), мы сначала выполним Rz (theta/2), затем контролируемое вращение вокруг оси X (CX), затем Rz (-theta/2) и снова CX.

Поскольку оператор X «разворачивает» направление вращения Rz, мы получим как раз нужный эффект зависимости от контрольного бита: если контрольный бит равен 0, композиция двух Rz с разными знаками «сократится», а если контрольный бит ненулевой, то они приплюсуются, и мы получим полное вращение Rz (theta).

Итоговый алгоритм следующий:

  1. Применяем H к первому кубиту,
  2. Поочерёдно для каждого последующего кубита:
    • Выполняем SWAP, чтобы в дальнейшем работать с ним,
    • Поочерёдно применяем Rk с каждым предыдущим кубитом в качественно контрольного,
    • Применяем H,
    • Повторяем SWAP, чтоб вернуть кубит на место.
  3. Применяем ко всему набору кубитов последовательность транспозиций SWAP, которые в композиции дают инверсию (т.е. переворачиваем массив).

Последний шаг, конечно, можно выполнить и на клиентской стороне, а не в квантовом коде.
Ниже приведён код эксплойта на Python (см. gist): 
from math import pi
from socket import socket

s = socket()
s.connect(('quantum.kelte.cc', 17171))

prog = ''

# Hadamard for the 0th qubit
prog += 'H\n'
for i in xrange(1, 8):
    # Take the ith qubit
    prog += 'SWAP %s\n' % i
    ids = list(range(i - 1, 0, -1)) + [i] # We have 0 swapped with i
    for j in xrange(len(ids)):
        theta = -pi / (2 ** j) / 4
        # Controlled (global phase adjusted) R1 implementation
        prog += 'Rz %f\n' % theta
        prog += 'CX %s\n' % ids[j]
        prog += 'Rz %f\n' % -theta
        prog += 'CX %s\n' % ids[j]
    # Apply Hadamard
    prog += 'H\n'
    # Swap back with the 0th qubit
    prog += 'SWAP %s\n' % i

# Reverse all the qubits
prog += '''SWAP 1
SWAP 6
SWAP 1
SWAP 2
SWAP 5
SWAP 2
SWAP 3
SWAP 4
SWAP 3
SWAP 7
'''

# Implement Hadamard
prog = prog.replace('H', 'Z Ry %f' % (pi / 2)).replace('\n', ' ')

s.recv(128)

s.send('%s\n' % prog.strip())

print(s.recv(56).strip().decode('hex'))

Запускаем и получаем флаг: ZN{Qu4NtuM_H3ll0_w0RLD_2021}.
Магия!

© Habrahabr.ru