Выразительная простота python на примере задач из комбинаторики
В процессе самообучения языку программирования python (имея знания с/с++) решил написать в качестве задания функции генерирующие элементы из различных множеств комбинаторных конфигураций. Конечно, можно справедливо заметить, что подобный функционал уже есть в стандартной библиотеке python в модуле itertools, но у каждого должно быть право изобрести велосипед, тем более в целях обучения…Тот кто знаком с основами теории вероятностей должны помнить, что такое урновые схемы и о чем эта таблица: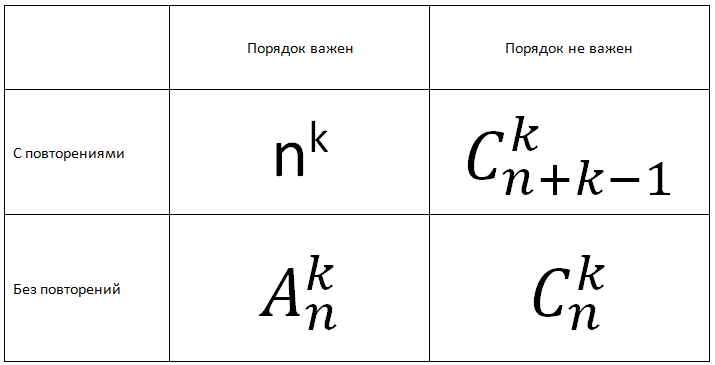 
И так ТЗ — написать четыре генератора, которые принимая строку s, состоящую из уникальных символов, и размер выборки к, возвращают строку — выборку с повторением/без повторений из k символов строки s порядок важен/не важен.В результате получился следующий код:
import math
def template (s, k, assertion = None, reducer = None): n = len (s) assert assertion (n, k) if k == 0: yield » return elif k == 1: for c in s: yield c return
k-=1 for i in range (n): c = s[i] new_s = reducer (s, i) if not assertion (len (new_s), k): break for res in template (new_s, k, assertion, reducer): yield c+res assertion_norep = lambda n, k: n > 0 and n >= k and k >= 0 assertion_rep = lambda n, k: n > 0 and k >= 0
def permutation_norep (s, k): return template (s, k, assertion = assertion_norep, reducer = lambda s, i: s[: i]+s[i+1:]) def permutation_rep (s, k): return template (s, k, assertion = assertion_rep, reducer = lambda s, i: s)
def combination_norep (s, k): return template (s, k, assertion = assertion_norep, reducer = lambda s, i: s[i+1:]) def combination_rep (s, k): return template (s, k, assertion = assertion_rep, reducer = lambda s, i: s[i:])
test = «abcdefg» k = 5 n = len (test) assert len (set (permutation_norep (test, k))) == (math.factorial (n) / math.factorial (n-k)) assert len (list (permutation_norep (test, k))) == (math.factorial (n) / math.factorial (n-k))
assert len (set (permutation_rep (test, k))) == n**k assert len (list (permutation_rep (test, k))) == n**k
assert len (set (combination_norep (test, k))) == (math.factorial (n) / (math.factorial (n-k)*math.factorial (k))) assert len (list (combination_norep (test, k))) == (math.factorial (n) / (math.factorial (n-k)*math.factorial (k)))
assert len (set (combination_rep (test, k))) == (math.factorial (n+k-1) / (math.factorial (n-1)*math.factorial (k))) assert len (list (combination_rep (test, k))) == (math.factorial (n+k-1) / (math.factorial (n-1)*math.factorial (k))) Так как python является языком еще более высокого уровня абстракции, чем с/с++, поэтому он позволяет проще и выразительнее писать код, который бы на других языках выглядел бы более громоздко и запутаннее. Новичкам в python я хотел бы обратить внимание на несколько моментов:
return после yield Рекурсивный генератор Шаблон стратегия Использование lambda функций P.S. Могу добавить, что я не сразу пришел к подобному решению, использующему общую «шаблонную» функцию. Сначала я написал все функции по отдельности, а потом выделил общее и различное.
