Введение в моделирование динамики квадро-, гекса- и октокоптеров28.09.2020 08:02

Что бы разбавить зубодробительную математику лекций Козлова Олега Степановича «Управление в технических системах», публикуем здесь пример применения знаний из этих лекций на практике.

В данной статье, Александр Щекатуров, ученик Олега Степановича описывает создание модели октокоптера, попутно раскрывая секреты и демонстрируя приемы работы в среде структурного моделирования физических систем.

В настоящей статье приведено описание логически завершённой, но всего лишь части полной работы по моделированию, но этой части достаточно для введения в тему динамического моделирования БПЛА коптерного типа.

Здесь опущено моделирование эффектов прецессии, принимается что и реактивный момент каждой ВМГ равен нулю, а именно: каждая ВМГ имеет два двигателя и винта, вращающихся с одинаковой скоростью в противоположные стороны. Не моделируются отказы оборудования и предполагается что объект находится только в воздухе (в штатном режиме полёта), режимы посадки и взлёта, аварийные ситуации, захват груза и разгрузка — в приведённой модели не реализованы, а также не рассматриваются вопросы подробного моделирования датчиков, фильтрации сигналов и шумов, изгиб рамы коптера и/или винтов, работа на запредельных нагрузках, написание драйверов к той или иной аппаратуре и т.д. и т.п., — всё это темы более расширенной статьи или даже книги.

Дано: объект массой порядка 10…25 кг, с 4, 6 или 8-ю парными соосными винтомоторными группами (ВМГ), расположенными по традиционной схеме квадро, гекса или октокоптера на жёсткой раме, с 8, 12 или 16 двигателями типа T-motors Antigravity 6007 KV320 или аналогичными и соответствующими им винтами (исходим из грузоподъёмности одной ВМГ порядка 2 кг на 50% газа). Предположим что конструкция аппарата до конца не определена.

Требуется: сконструировать и реализовать модель динамики объекта параметрически, в общем виде и в объёме, достаточном для проектирования полётного контроллера и наземного пульта управления коптером.

В литературе и сети приведено довольно много моделей квадрокоптеров, есть некоторые модели гекса- и октокоптеров. Однако, изложенного в системном и методичном виде со всеми подробностями — практически ничего нет (по крайней мере, в русскоязычном сегменте, из тех материалов что удалось найти). Наиболее методично теоретический подход к моделированию мультироторного БПЛА изложен в работах [1] и [2].

Опуская некоторые выкладки, изложенные в этих работах (они легко гуглятся), можно выделить следующие допущения и упрощения, принятые в модели:

Двигатель моделируется как инерционное звено (апериодическое звено) первого порядка, на вход которому подается заданное значение угловой скорости, а на выходе — текущее (измеренное) значение угловой скорости вращения. Интегрируя скорость вращения, можно получить и текущий угол поворота если это зачем-то нужно. Силу тяги ВМГ развивает пропорциональную квадрату угловой скорости (равно как и реактивный момент каждого двигателя, но в нашем случае он будет 0), а именно:
$F_M(t)=C_T \cdot \omega^2(t), \\ M_M(t)=C_Q \cdot \omega^2(t),$

где, для выбранной винтомоторной группы (согласно её характеристике):
$C_T=2.02268 \cdot 10^{-4}H \cdot c^2$ ,
$M_M ≈0 \ \ Н \cdot м\cdot с^2$ — реактивный момент двигателя,
— текущая угловая скорость, рад/с.
Мультироторный аппарат моделируется как твёрдое тело и представляет собой жёсткую (недеформируемую) раму постоянной массы, симметричную по трём главным осям, с прикрепленными к ней ВМГ в одной плоскости, в которой находится и центр масс аппарата. При этом ВМГ расположены на восьми лучах (4 из них одной длины, а другие 4 могут быть другой длины) и жестко закреплены относительно рамы. Таким образом можно говорить о том, что радиус-векторы центров ВМГ и орты силы тяги каждой ВМГ — суть геометрические константы в системе координат, связанной с коптером. Другими словами, величина [Н], вычисленная в модели ВМГ, является модулем вектора силы, приложенного всегда в определенном направлении и в определенной точке коптера. В процессе полета это направление будет меняться, конечно, но относительно рамы коптера (и связанной с ней системы координат) оно остаётся неизменным.
Используется две системы координат: а) неподвижная инерциальная, связанная с Землёй и б) подвижная, связанная с коптером. Системы координат обозначим буквами I и B (от английских слов inertial — инерциальный и body — тело). При этом оси систем направлены: -вправо, -на наблюдателя, -вниз, — вправо вдоль луча первой ВМГ, -на наблюдателя вдоль луча третьей ВМГ, -сверху вниз при нормальной ориентации коптера (см. рисунок):

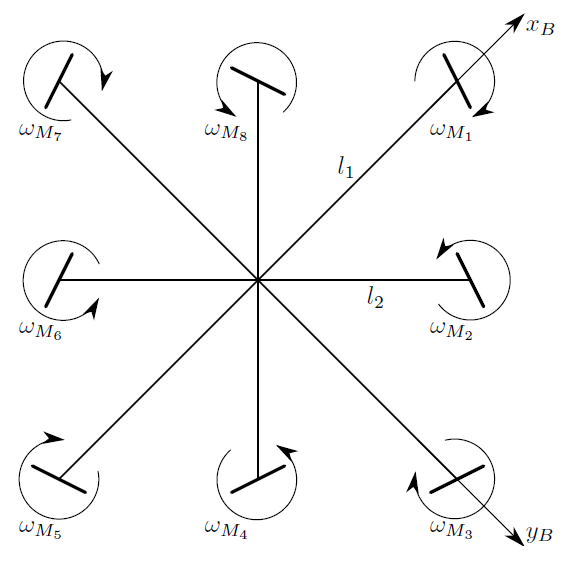
Тогда, в системе координат B векторы центров ВМГ будут равны:
$\vec {r_{M1}} = (l_1,0,0)^T, \ \ \ \ \vec {r_{M2}}=\frac{1}{\sqrt 2} (l_2,l_2,0)^T \\ \vec {r_{M3}} = (0,l_1,0)^T, \ \ \ \ \vec {r_{M4}}=\frac{1}{\sqrt 2} (-l_2,l_2,0)^T \\ \vec {r_{M5}} = (l_1,0,0)^T, \ \ \ \ \vec {r_{M6}}=\frac{1}{\sqrt 2} (-l_2,-l_2,0)^T \\ \vec {r_{M7}} = (0,-l_1,0)^T, \ \ \ \ \vec {r_{M8}}=\frac{1}{\sqrt 2} (l_2,-l_2,0)^T$

где — длина луча у 1, 3, 4 и 5-й ВМГ, а — длина лучей у 2, 4, 6 и 8-й ВМГ.
Для того чтобы коптер управлялся (хотя бы немного) по курсу, в нашем случае отсутствия реактивного момента двигателей, вектора сил тяги каждой ВМГ должны быть немного отклонены от вертикального направления (повёрнуты вокруг каждого луча на небольшой угол порядка 1…5 градусов, причем в разные стороны — четные в одну, а нечетные в другую). Если обозначить этот угол как $\gamma$ , орты можно получить в следующем виде:
$\vec{e_{M1}}=(0,-sin(\gamma),-cos(\gamma))^T, \ \ \ \vec{e_{M2}}=(-\frac{sin(\gamma)}{\sqrt2},\frac{sin(\gamma)}{\sqrt2},-cos(\gamma))^T,\\ \vec{e_{M3}}=(sin(\gamma),0,-cos(\gamma))^T, \ \ \ \vec{e_{M4}}=(-\frac{sin(\gamma)}{\sqrt2},-\frac{sin(\gamma)}{\sqrt2},-cos(\gamma))^T,\\ \vec{e_{M5}}=(0,sin(\gamma),-cos(\gamma))^T, \ \ \ \vec{e_{M6}}=(\frac{sin(\gamma)}{\sqrt2},-\frac{sin(\gamma)}{\sqrt2},-cos(\gamma))^T,\\ \vec{e_{M7}}=(-sin(\gamma),0,-cos(\gamma))^T, \ \ \ \vec{e_{M8}}=(\frac{sin(\gamma)}{\sqrt2},\frac{sin(\gamma)}{\sqrt2},-cos(\gamma))^T.$

На основе этих геометрических констант (напомним, они являются константами только в системе координат B, связанной с коптером) строится весь дальнейший каркас модели, поэтому они важны. В общем случае, винтомоторных групп может быть другое количество и направлены они могут быть в других направлениях, и располагаться у коптера в других местах.
О применяемых системах координат подробно изложено в [1].
Силы, которые будут учтены в модели. На коптер действуют:
4.1) Сила тяжести. Направлена всегда вниз вдоль оси инерциальной системы координат . Сила тяжести — постоянная величина, зависит только от массы коптера. Масса коптера принимается постоянной и не меняется (хотя в процессе моделирования её можно будет менять, имитируя дополнительный полезный груз, навешенный на коптер).
4.2) Силы тяги ВМГ — их всего 8, они направлены вдоль своих направлений, модуль сил вычисляется в зависимости от угловой скорости вращения соответствующей ВМГ.
4.3) Сила сопротивления воздуха (и/или ветер) — моделируется как состоящая из двух компонент. Сила сопротивления воздуха прямо пропорциональна плотности воздуха, квадрату линейной скорости объекта в воздухе и характерной площади сечения в выбранном направлении (коэффициент формы). Сила ветра — внешняя возмущающая сила, задается произвольным образом или при помощи дополнительной «модели ветра» (в настоящей статье не рассматривается).
4.4) Внешняя сила или возмущение — произвольное внешнее воздействие. В модели такая возможность заложена как простой способ в дальнейшем проверять на устойчивость регуляторы по каждому из направлений.
Моменты, учитываемые в модели:
5.1) Реактивный момент двигателей ВМГ. В нашей модели он равен нулю, из-за парности двигателей и винтов в каждой ВМГ в общем случае — следует учитывать. В некоторых аппаратах этот момент используется и для управления по курсу.
5.2) Явление прецессии — в рассматриваемой модели он нулевой, в общем случае его нужно считать.
5.3) Момент сопротивления воздуха — аналогично силе сопротивления воздуха, прямо пропорционален плотности воздуха, квадрату угловой скорости коптера и коэффициенту формы.
5.4) Опрокидывающий момент от ветровой нагрузки.
5.5) Внешний возмущающий момент — для отладки регуляторов.
5.6) Моменты от сил тяги ВМГ. Поскольку винты расположены не в центре масс коптера, каждый из них будет создавать свой поворотный момент. Это, пожалуй, основной фактор, который управляет ориентацией коптера в пространстве.

С учетом принятых допущений, и того что коптер моделируется как единое твёрдое тело, основа модели динамики коптера очень проста — это второй закон Ньютона, который в векторной форме выглядит следующим образом, всего два простых уравнения:

$\frac{d \vec{p}(t)}{dt}=\vec{F}(t), \\ \frac{d \vec{L}(t)}{dt}=\vec{M}(t),$

где $\vec {p}(t))=m \cdot \vec{v}(t)$ — импульс коптера, а $\vec{L} (t)=I(t)\cdot \vec{\omega}(t)$ — момент импульса коптера, $m$ — его масса, $I(t)$ — тензор инерции (линейный оператор момента инерции). $\vec{F}(t)$ и $\vec{M}(t)$ суть суммы всех сил и всех моментов, действующих на коптер.

Легко видеть, что всё было бы очень просто и очевидно, если бы правые части были небольшими, а тензор инерции не зависел бы от ориентации коптера (как если бы коптер был шаром). Но из-за вращения коптера, а также из-за обилия сил и моментов, конечные уравнения, записанные в инерциальной системе координат, получатся очень громоздкими, даже без учета прецессии и реактивных моментов ВМГ. Поэтому используется следующий математический приём — уравнения, записанные в инерциальной системе координат, переводятся в систему координат B, связанную с коптером, в которой слагаемые правой части (их запись) получается гораздо более лаконичной и удобной. Подробнее этот приём описан в [1], приведём здесь лишь основные соотношения.

Подставив в приведенные уравнения второго закона Ньютона значения для импульса и момента импульса коптера, для инерциальной системы координат получим:

$\frac{d \vec{v_I}(t)}{dt}=\frac{1}{m}\vec{F_I}(t),\\ \frac{d \vec{\omega_I}(t)}{dt}= I^{-1}(\vec{M_I}(t)-\frac{dI_I}{dt}\cdot \vec{\omega_I}).$

В этих уравнениях математически очень сложны правые части, а уравнения динамики в связанной системе координат B (где правые части более просты) — не могут быть получены так легко, поскольку система координат, связанная с коптером — вращается.

В математике есть два основных подхода к преобразованию векторов из одной системы координат в другую и обратно — матрицы поворота и кватернионы. Последние более универсальны, первые — проще. В настоящей модели используются матрицы поворота. Если ориентацию коптера представить тремя углами: крена φ (roll), тангажа θ (pitch) и рыскания/курса ψ (yaw), а матрицы преобразования из системы I в B и обратно обозначить как $R_{IB}$ и $R_BI=R_IB^T$ , то любой вектор записанный для системы координат I, можно перевести в систему координат B, и наоборот, используя умножение соответствующей матрицы на вектор, например: $\vec{F_I }(t)=R_{BI} \vec{F_B}(t)$ , или $\vec{F_B }(t)=R_{IB} \vec{F_I}(t)$ .

Чтобы лучше понимать написанное далее, прокомментируем ещё раз как понимать матрицы поворота и вектора в пространстве: система координат I неподвижна, относительно неё летает и вращается коптер, а вместе с ним и связанная система координат B. Просуммировав все силы, которые действуют на коптер, можно получить вектор $\vec F(t)$ (аналогично и с моментом сил), и в каждый момент времени он является вектором с вполне определенной длиной и направлением в пространстве. Но раскладывая его на проекции по осям — в разных системах координат мы получим разные величины проекций. Всё что делает матрица поворота — это переводит одни проекции вектора в другие, при этом сам вектор никуда не поворачивается и не изменяет своей длины, в выбранный момент времени. Если проекции сравнить с тенями вектора, то матрицы поворота преобразуют одни тени в другие, всё. Больше они ничего не делают и сложностей кроме вычислительных не представляют.

Нам они нужны только из-за того, что вычислять и суммировать силы и моменты сил, действующие на коптер, гораздо проще в связанной системе координат B. В ней же проще провести численное интегрирование уравнений, чтобы получить величины угловой и линейной скоростей коптера $\vec{ω_B}(t)$ и $\vec{v_B}(t)$ , а потом обратной матрицей поворота вычислить (вычислить алгебраически — матрицы поворота это простые уравнения) эти же скорости для инерциальной системы координат I и там уже, интегрируя дальше, вычислить линейные и угловые координаты коптера.

Приведем используемое выражение для матрицы поворота из системы I в B, записав для краткости функции косинуса и синуса как cos () = c () и sin () = s ():

$R_{IB}=\\ =\left( \begin{array}{ccc} c(\theta)\cdot s(\psi) & c(\theta)\cdot s(\psi) & -s(\theta)\\ s(\varphi) \cdot s(\theta) \cdot c(\psi)- c(\varphi) \cdot s(\psi)&s(\varphi) \cdot s(\theta) \cdot s(\psi) + c(\varphi) \cdot C(\psi) & s(\varphi) \cdot c(\theta)\\ c(\varphi) \cdot s(\theta) \cdot c(\psi) + s(\varphi) \cdot s(\psi)&s(\varphi) \cdot s(\theta) \cdot s(\psi) - s(\varphi) \cdot c(\psi) & c(\varphi) \cdot c(\theta) \end{array} \right)$

Отметим еще раз, что в каждый момент времени эта матрица, очевидно, будет получаться разной т.к. меняются углы ориентации коптера. Но это просто алгебраические вычисления, без никаких дифференциальных уравнений. Сама матрица — не константа, и у неё есть производная по времени.

Реализованная методом структурного моделирования, матрица в среде SimInTech выглядит как показано на рисунке 1.

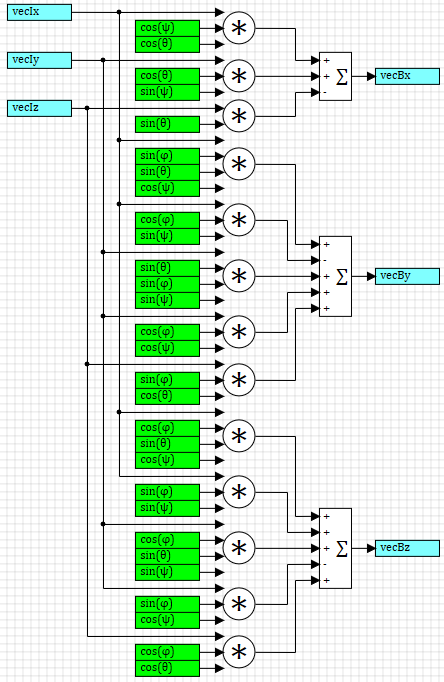
Рисунок 1. Матрица поворота из системы I в систему координат B

Тогда, для вектора линейной скорости можно записать:

$\vec {v_B} (t)=R_{IB} \cdot \vec {v_I}(t),$

, а для момента импульса

$\vec {L_B} (t)=R_{IB} \cdot \vec{L_I }(t).$

Опуская промежуточные выкладки (в том числе производную матрицы поворота, которая получается равной в итоге векторному произведению угловой скорости объекта на саму матрицу поворота, взятое с обратным знаком), для первого из рассматриваемых уравнений динамики получим следующее выражение в связанной с коптером системе координат B:

$\frac{d\vec{v_B}}{dt} =- \vec{\omega_B}(t) \times \vec{v_B}(t)+ \frac{1}{m}\vec{F_B}(t),$

а для второго уравнения, учитывая что $\vec{L_B } (t)=I_B\cdot \vec{\omega_B} (t)$ ,
и так как во вращающейся связанной системе координат тензор инерции константа и его производная по времени равна нулю, а $\frac{d\vec{L_B } (t)}{dt}=I_B\cdot \frac{d\vec{\omega_B} (t)}{dt}$ получим:

$\frac{d\vec{\omega_B}}{dt} =-I_B^{-1}( \vec{M_B}(t) - \vec{\omega_B}(t) \times (I_B \cdot \vec{\omega_B}(t))).$

Итого, запись II закона Ньютона для вращающейся системы B, по сравнению с исходными уравнениями, дополнилась двумя векторными произведениями.

Переменными состояния коптера в такой записи являются две векторных величины (или 6 скалярных) — вектор линейной скорости и вектор угловой скорости. Алгебраически это будет 6 переменных — три проекции линейной скорости и три проекции угловой скорости. И мы имеем записанную в форме Коши систему из 6 нелинейных уравнений первого порядка, которую легко можно реализовать в среде структурного моделирования SimInTech или Simulink или Scilab и даже успешно решить её тем или иным методом интегрирования.

Получив значения скоростей коптера (сначала в системе B), их можно матрицей обратного поворота преобразовать к системе I, еще раз проинтегрировать и получить уже значения координат и, следовательно, положение объекта в пространстве, в инерциальной системе координат.

Единственное что мы еще не сделали по уравнениям — не записали выражения для сил и моментов, действующих на коптер. Сделаем это ниже, в системе координат B. Согласно допущениям, учитываем и обозначим индексами: M — работу двигателей, только в части создаваемой силы тяги и моментов от неё, D — силу сопротивления воздуха (вместе с ветром), O — внешнее возмущение, вообще нулевое, и задаваемое произвольно пользователем, силу тяжести — она поворотного момента сил не создаёт:

$\vec {F_B}(t) = \vec {F_M}(t)+\vec {F_D}(t)+\vec {F_O}(t)+m\cdot g \cdot R_{IB}\cdot\vec{e_{IZ}}\\ \vec {M_B}(t) = \vec {M_M}(t)+\vec {M_D}(t)+\vec {M_O}(t)$

Сила тяжести в связанной системе координат будет «поворачиваться» в зависимости от ориентации коптера.

Распишем подробнее чему равны слагаемые:

$\vec {F_M}(t) = C_T\cdot\omega_{M1}^2(t)\cdot \vec {e_{M1}}+ C_T\cdot\omega_{M2}^2(t)\cdot \vec {e_{M2}}+ C_T\cdot\omega_{M3}^2(t)\cdot \vec {e_{M3}}+\\ +C_T\cdot\omega_{M4}^2(t)\cdot \vec {e_{M4}}+ C_T\cdot\omega_{M5}^2(t)\cdot \vec {e_{M5}}+ C_T\cdot\omega_{M6}^2(t)\cdot \vec {e_{M6}}+\\ +C_T\cdot\omega_{M7}^2(t)\cdot \vec {e_{M7}}+ C_T\cdot\omega_{M8}^2(t)\cdot \vec {e_{M8}}$

Здесь уже фигурируют угловые скорости вращения ВМГ, а не коптера. Напомним, что орты сил тяги у нас записаны для системы координат B и там являются константами — очевидно, что их можно вычислить 1 раз, общий коэффициент вынести здесь за скобку и сильно упростить вычисления. Если бы мы записывали уравнения динамики в системе I, то данное выражение обросло бы ещё 8-ю умножениями на матрицу поворота каждого орта и это пришлось бы считать на каждом шаге расчета.

Сила сопротивления воздуха (при отсутствии ветра):

$\vec{F_{D}} =-0.5 \rho \cdot C_D \cdot \left( \begin{array}{c} A_{yz}\cdot v_x \cdot |v_x|\\ A_{xz}\cdot v_y \cdot |v_y| \\ A_{xy}\cdot v_z \cdot |v_z| \end{array} \right)$

Внешнее возмущение — нулевое, по желанию пользователя, он может сам установить то или иное значение позже, до расчета, или в процессе моделирования.

Момент сил тяги двигателей запишем как:

$\vec {M_M}(t) =\vec{r_{M1}} \times \vec {e_{M1}} \cdot C_T\cdot\omega_{M1}^2(t) + \vec{r_{M2}} \times \vec {e_{M2}} \cdot C_T\cdot\omega_{M2}^2(t)+\\ +\vec{r_{M3}} \times \vec {e_{M3}} \cdot C_T\cdot\omega_{M3}^2(t)+ \vec{r_{M4}} \times \vec {e_{M4}} \cdot C_T\cdot\omega_{M4}^2(t)+\\ +\vec{r_{M5}} \times \vec {e_{M5}} \cdot C_T\cdot\omega_{M5}^2(t)+ \vec{r_{M6}} \times \vec {e_{M6}} \cdot C_T\cdot\omega_{M6}^2(t)+\\ \vec{r_{M7}} \times \vec {e_{M7}} \cdot C_T\cdot\omega_{M7}^2(t)+ \vec{r_{M8}} \times \vec {e_{M8}} \cdot C_T\cdot\omega_{M8}^2(t)$

Момент сопротивления воздуха (подробнее см. [1]):

$\vec{M_{D}} =-0.5 \rho \cdot C_D \cdot \left( \begin{array}{c} A_{yz}\cdot v_x \cdot |v_x| \cdot l_x\\ A_{xz}\cdot v_y \cdot |v_y| \cdot l_y\\ 8A_{xy}\cdot v_z \cdot |v_z| \cdot l_z \end{array} \right)$

Ещё раз отметим, что расчет прецессии и реактивных моментов ВМГ в данной статье для краткости изложения опущен.

Чтобы не ошибиться при переходе от векторных уравнений к скалярным, записанным по осям, проще воспользоваться пакетом типа MathCAD или Maple, в котором большинство преобразований можно выполнить автоматизированно, в символьном виде и получить требуемые 6 уравнений динамики, записанные по осям подвижной системы координат B.

В наиболее компактной форме полученные и решаемые уравнения динамики выглядят так:

$\frac{d\vec{v_B}}{dt}=\frac{1}{m}\left(\vec{F_M}(t) +\vec{F_D}(t) + \vec{F_O}(t)\right)+ gR_{IB}\vec{e_Iz} -\vec{\omega_B}(t)\times\vec{v_B}(t),\\ \frac{d\vec{\omega_B}}{dt} = I_B^{-1}\left (\vec{M_M}(t) +\vec{M_D}(t)- \vec{\omega_B}(t)\times(I_B\cdot\vec{\omega_B}(t) \right).$

Интегрируя их и получив значения скоростей в системе В, можно посчитать скорость и углы ориентации в инерциальной системе координат I:

$\vec{v_I}(t) = R_{BI}\cdot \vec{v_B}(t),\\ \left( \begin{array}{c} \dot{\varphi} \\ \dot{\theta} \\ \dot{\psi} \end{array} \right) = W_{BI} \cdot\vec{\omega_B}(t).$

Про матрицу преобразования из угловой скорости коптера в скорости поворота по углам Эйлера $W_{BI}$ подробнее см. в [1].

Переходим к самому интересному — к реализации полученных уравнений динамики средствами среды динамического моделирования SimInTech. Как известно, любую задачу можно всегда решить несколькими способами, и чем она сложнее и многомернее — тем больше количество способов. В настоящей статье предложен один из вариантов решения, он не единственный, и в некоторых местах — не самый оптимальный. Выбор решения определялся простотой реализации с одной стороны, и удобством для методичного рассказа, с другой.

Итак, что мы получили с точки зрения математики — в системе координат B мы имеем 2 векторных дифференциальных уравнения, которые при переходе к проекциям (и скалярным уравнениям) дают 6 нелинейных дифференциальных уравнений первого порядка, относительно 6 переменных: трёх скоростей и трёх угловых скоростей. Это так называемая 6DOF задача, т.е. задача с шестью степенями свободы. Сначала можно подумать, что раз у коптера имеется 6 степеней свободы, то должно быть и 6 переменных состояния (дифференциальных переменных). Но это так только на первый взгляд. Кроме скоростей, дальше нам придется получить еще и координаты (три линейных и три угла положения в пространстве) — для чего еще раз проинтегрировать скорости. Таким образом, всего у коптера есть 12 степеней свободы. А если учесть еще то, что правые части дифференциальных уравнений есть ни что иное как ускорения коптера по осям, то получим как бы 18 степеней свободы. Это важно понимать, так как в дальнейшем для построения регулятора нам потребуются все 12 фазовых координат объекта плюс ещё 6 измеренных (или вычисленных) ускорения коптера.

3.1 Решение дифференциальных уравнений методом структурного моделирования

Для решения дифференциального уравнения методом структурного моделирования используются либо типовые звенья первого и второго порядков — если дифференциальное уравнение линейно и подходит под один из типов, либо используется блок типа «Интегратор», на вход которому подаётся правая часть уравнения, а на выходе будет искомая интегральная величина. Приведём пример — заготовку для решения нашей системы из 6-ти дифференциальных уравнений, см. рисунок 2.

На рисунке 2 представлена «основа» динамической части модели октокоптера, которую формируют 6+3+3 блоков типа «интегратор». Первые шесть блоков, получая на вход правые части дифференциальных уравнений (вычислим их ниже) — ускорения коптера по осям $a_{Bx},a_{By},a_{Bz},ω_{Bx},ω_{By},ω_{Bz}$ , — занимаются интегрированием и вычислением скоростей коптера по этим же осям (тоже, в связанной с коптером системе В).

Следующие три интегратора принимают линейные скорости в системе координат I (полученные алгебраически из скоростей в системе B путём применения матрицы поворота) и, интегрируя их, получают координаты центра масс коптера в инерциальной системе координат

И, еще три блока типа «интегратор» занимаются вычислением углов ориентации коптера, интегрируя их производные (угловые скорости) в системе I, полученные из угловых скоростей коптера в системе B применением матрицы $W_{BI}$ . Здесь же реализовано и вычисление нужных тригонометрических функций от углов поворота.

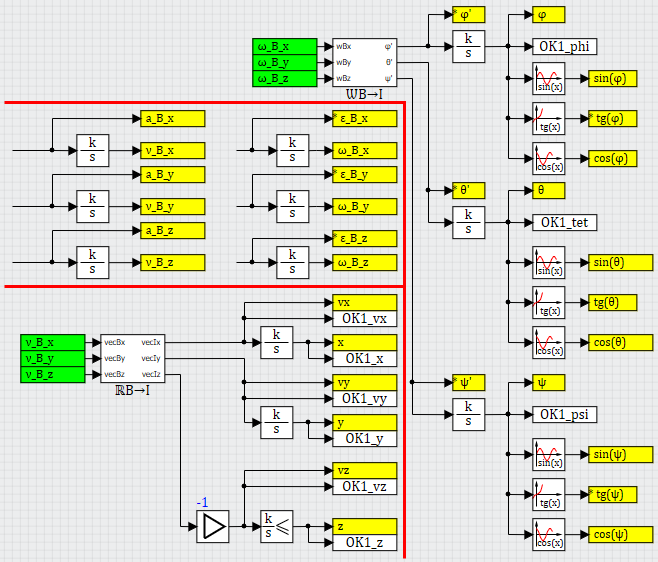
Рисунок 2. Структура модели октокоптера

Обилие блоков «в память» и «из памяти» обусловлено многократным использованием в других частях модели полученных величин — например, по рисунку 1 видно что тригонометрические функции от углов ориентации используются многократно и оптимально вычислить их в одном месте схемы, а потом уже использовать по мере необходимости.

Если бы у нас была более простая ситуация — одно дифференциальное уравнение второго порядка (классический второй закон Ньютона a = F/m), например в проекции на ось x, то его решение таким же способом выглядело бы как на рисунке 3:

Рисунок 3. Двойное интегрирование

В случае коптера используется такой же приём, т.е. если на выходе из интегратора имеется какая-то величина, то слева от него — обязательно производная этой же величины. Таким образом записываются и решаются дифференциальные уравнения методом структурного моделирования, если не прибегать к встроенному языку программирования SimInTech (где зачастую удаётся сделать то же самое еще более просто, но менее очевидно).

В субмодели W (B→I) реализована матрица преобразования из угловой скорости в системе B в производные углов Эйлера, см. рисунок 4 и [1] для подробностей.

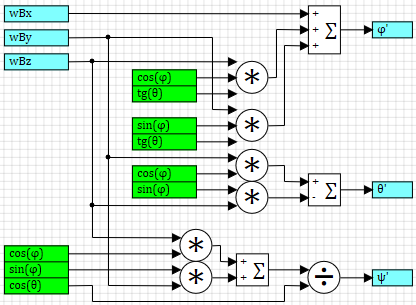
Рисунок 4. Матрица $W_{BI}$

3.2 Правые части уравнений модели коптера

Для замыкания модели необходимо посчитать и реализовать все правые части у шести основных уравнений, то есть спроецировать полученные в разделе 2 векторные уравнения на оси $x_B,y_B,z_B$ и результат нарисовать в схеме SimInTech. Опуская выкладки (их читатель может выполнить самостоятельно на листке бумаги, или при помощи какого-то символьного математического ПО), приведем окончательный вид уравнений. Из-за громоздкости, приводить будем по слагаемым в правых частях.

Сила тяги винтомоторных групп $\vec{F_M }(t):$

$F_{Мх}(t)=\frac{1}{\sqrt{2}} \left(-F_{М2}(t)-F_{M4}(t)+F_{M6}(t)+F_{M8}(t)\right) \cdot sin(\gamma)+\\ +\left(F_{M3}(t)-F_{M7}(t) \right)\cdot sin(\gamma),\\ F_{Му}(t)=\frac{1}{\sqrt{2}} \left(F_{М2}(t)-F_{M4}(t)-F_{M6}(t)+F_{M8}(t)\right) \cdot sin(\gamma)+\\ + \left( F_{M5}(t)-F_{M1}(t) \right ) \cdot sin(\gamma),\\ F_{Мz}(t)= \left(F_{M1}(t)+F_{М2}(t)+F_{M3}(t)+F_{M4}(t)+\\ +F_{M5}(t)+F_{M6}(t)+F_{M8}(t)+F_{M8}(t)\right) \cdot cos(\gamma),$

где $F_{Mi}(t)$ — сила тяги i-ой ВМГ в текущий момент времени.

Сила сопротивления воздуха $\vec{F_D}(t)$ при отсутствии ветра — формулы приведены выше, проекции будут равны:

$$display$$F_{Dx}(t) = 0.5 \cdot \rho \cdot C_D\cdot A_{yz}\cdot v_x\cdot |v_x|,\\ F_{Dу}(t) = 0.5 \cdot \rho \cdot C_D\cdot A_{xz}\cdot v_у\cdot |v_у|,\\ F_{Dz}(t) = 0.5 \cdot \rho \cdot C_D\cdot A_{xy}\cdot v_z\cdot |v_z|.\\$$display$$

Сила тяжести, в проекции на оси подвижной системы координат, слагаемое $g\cdot R_{IB}\cdot \vec {e_{Iz}}$ очевидно будет равно:

$g\cdot R_{IB}\cdot \vec {e_{Iz}} =\left( \begin{array}{c} -sin(\theta)\\ sin(\phi)\cdot cos(\theta) \\ cos(\phi)\cdot cos(\theta) \end{array} \right)$

И последнее слагаемое в уравнении линейной скорости коптера — векторное произведение скоростей:

$-\vec{\omega_B}(t)\times \vec{v_B}(t) =\left( \begin{array}{c} v_{Bz}\cdot \omega_{By} - v_{By} \cdot \omega_{Bz} \\ v_{Bx}\cdot \omega_{Bz} - v_{Bz} \cdot \omega_{Bx} \\ v_{By}\cdot \omega_{Bx} - v_{Bx} \cdot \omega_{By} \end{array} \right).$

Если аккуратно подставить полученные проекции в уравнение для производной линейной скорости коптера, и дальше реализовать всё это в SimInTech, по осям, получим следующие структурные схемы, представленные на рисунках 5, 6 и 7 (показаны проекции только на ось $x_B$ , на другие оси результат аналогичен с точностью до слагаемых):

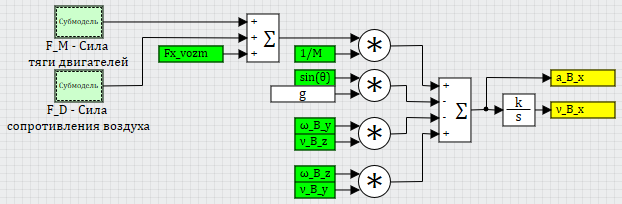
Рисунок 5. Линейное ускорение коптера по оси $x_{B}$ .

Рисунок 6. Сила тяги ВМГ по оси $x_{B}$ .

Рисунок 7. Сила сопротивления воздуха по оси $x_{B}$ .

Итого, на данном этапе мы до конца реализовали одно из шести основных уравнений (согласно рисунку 2 — вычислили вход в первый интегратор). Остальные оборванные там входы для сил вычисляются аналогично. Рассмотрим уравнение для моментов и для вычисления угловой скорости, а точнее — его слагаемые в правой части:

$\vec{M_m}(t)+\vec{M_D}(t)-\vec{\omega_B}(t) \times(I_B \cdot \vec{\omega_B})$

Сумма моментов сил тяги всех ВМГ:

$M_{Mx}(t)=\left[ \frac{l_2}{\sqrt2} \left( -F_{M2}(t)-F_{M4}(t)+F_{M6}(t)+F_{M8}(t) \right) +\\ +l_1(F_{M7}(t)-F_{M3}(t))\right] \cdot cos(\gamma), \\ M_{Mу}(t)=\left[ \frac{l_2}{\sqrt2} \left( F_{M2}(t)-F_{M4}(t)-F_{M6}(t)+F_{M8}(t) \right) +\\ +l_1(F_{M1}(t)-F_{M5}(t))\right] \cdot cos(\gamma),\\ M_{Mz}(t)= \left[ l_2 ( F_{M2}(t)+F_{M4}(t)+F_{M6}(t)+F_{M8}(t)) +\\ -l_1(F_{M1}(t)+F_{M3}(t)+F_{M5}(t)+F_{M7}(t)) \right] \cdot sin(\gamma).$

где $F_{Mi} (t)$ — сила тяги i-ой ВМГ в текущий момент времени, $l_1,l_2$ -плечи сил (длины лучей рамы коптера для нечетных и четных ВМГ).

Момент сопротивления воздуха (при отсутствии ветра):

$M_{Dx}(t) = 0.5 \cdot \rho \cdot C_D\cdot A_{yz}\cdot \omega_{Bx}\cdot |\omega_{Bx}|\cdot l_x,\\ M_{Dу}(t) = 0.5 \cdot \rho \cdot C_D\cdot A_{xz}\cdot \omega_{By}\cdot |\omega_{By}|\cdot l_y,\\ M_{Dz}(t) = 0.5 \cdot \rho \cdot C_D\cdot 8\cdot A_{xy}\cdot \cdot \omega_{Bz}\cdot |\omega_{Bz}|\cdot l_z.$

Векторное произведение угловой скорости на произведение тензора инерции и угловой скорости:

$-\vec{\omega_B}(t)\times (I_B \cdot\vec{\omega_B}(t)) =\left( \begin{array}{c} (I_{yy}-I_{zz})\cdot \omega_{By}\cdot \omega_{Bz} \\ (I_{zz}-I_{xx})\cdot \omega_{Bx}\cdot \omega_{Bz} \\ (I_{xx}-I_{yy})\cdot \omega_{Bx}\cdot \omega_{By} \end{array} \right).$

Итого, после подстановки этих слагаемых в дифференциальное уравнение для угловой скорости, и реализации полученного в среде SimInTech, получим следующие структурные схемы:

Рисунок 8. Угловое ускорение коптера вокруг оси $x_{B}$ .

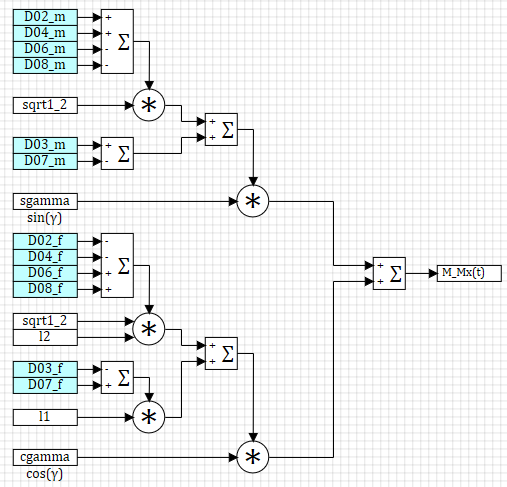
Рисунок 9. Момент сил тяг ВМГ вокруг оси $x_{B}$ .

Рисунок 10. Сила сопротивления воздуха при вращении вокруг $x_{B}$ .

3.3 Система уравнений динамики октокоптера в структурном виде

Итого, если представить все реализованные уравнения рядом на схеме, получим следующую картину (рисунок 11). Как видно, она довольно громоздка, даже без включения сюда других дифференциальных уравнений для вычисления координат коптера и углов поворота. А поскольку в дальнейшем на каждое уравнение будут навешиваться еще дополнительные сервисные вычисления (ускорений, различных составляющих сил и моментов, для отладки модели и регуляторов), целесообразнее эти уравнения структурно разделить на 6+ субмоделей, что и было сделано, в каждой из которых решается своё уравнение, см. рисунок 12.

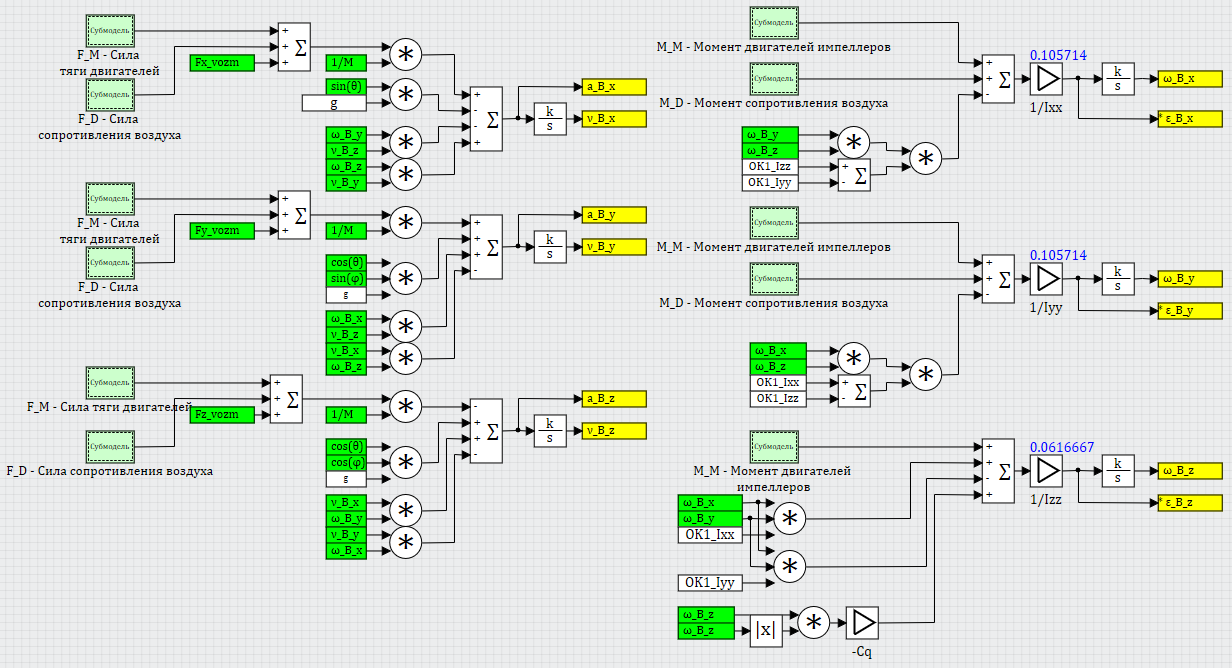
Рисунок 11. Уравнения динамики коптера в связанной системе координат В.

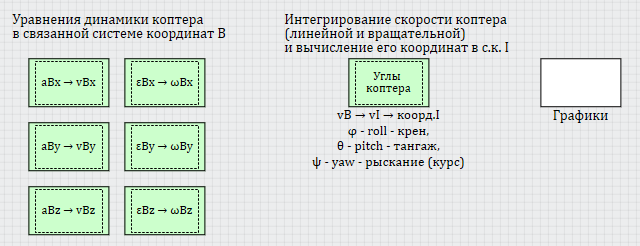
Рисунок 12. Модель динамики коптера, верхний уровень.

В принципе, все приведенные уравнений и структуры можно было реализовать и средствами языка программирования SimInTech, но тогда они были бы не так наглядны.

Входными величинами здесь являются силы тяги двигателей (они считаются вне этих уравнений, в зависимости от текущей скорости вращения каждой ВМГ и её силовой характеристики), внешняя возмущающая сила и момент сил (задаются пользователем произвольно) и сила тяжести. Также, возможно ещё влияние ветра/прецессия/реактивный момент или что-то ещё — в настоящей статье это не рассматривается, для краткости мы ограничились силами тяги двигателей и притяжения Земли.

Выходными величинами являются ускорения, скорости и положение (координаты) коптера — ускорения и скорости в системах координат B и I, положение — в системе I (положение коптера в системе B практической ценности почти не имеет т.к. сама система движется вместе с коптером и совпадает по положению с ним — то есть там положение коптера всегда будет нулевым).

В продолжении мы рассмотрим создание системы