Введение в криптографию и шифрование, часть вторая. Лекция в Яндексе
Под катом — расшифровка и часть слайдов.
— Реальная ситуация следующая: коллизия между двумя выборками случайных чисел длиной 256 бит достигнет вероятности ½ примерно при 4 миллиардах выборок. Значит, если мы рассматриваем поток блоков длиной 64 случайных бита, то с вероятностью ½ среди 232 таких блоков найдутся два одинаковых.
Какое прикладное значение имеет указанный научный факт? Выход функции шифрования можно рассматривать как случайное число, и идеальная функция шифрования неотличима от случайного числа. Значит, если мы рассматриваем блоки, зашифрованные, например, алгоритмом DES или ГОСТ-28147, то взяв 232 таких блоков, мы с вероятностью ½ обнаружим, что два из них зашифрованы одинаково.
Давайте кто-то посчитает: 232 блоков размером 64 бита или 8 байт — это сколько? 32 гигабайта? Похоже на правду. Теперь поделим 32 гигабайта на 10 гигабит. Если у нас есть алгоритм шифрования с 64-битными блоками, то чуть позже, чем через 32 секунды, мы увидим коллизию. Мы увидим два блока, которые зашифровались одинаково. Как выяснили в СВС, указанные два блока необязательно должны быть с одинаковым открытым текстом. Открытый текст может быть разным.
Что это будет значить? Если у нас есть какой-то блок Ci, то что было зашифровано в режиме СВС? 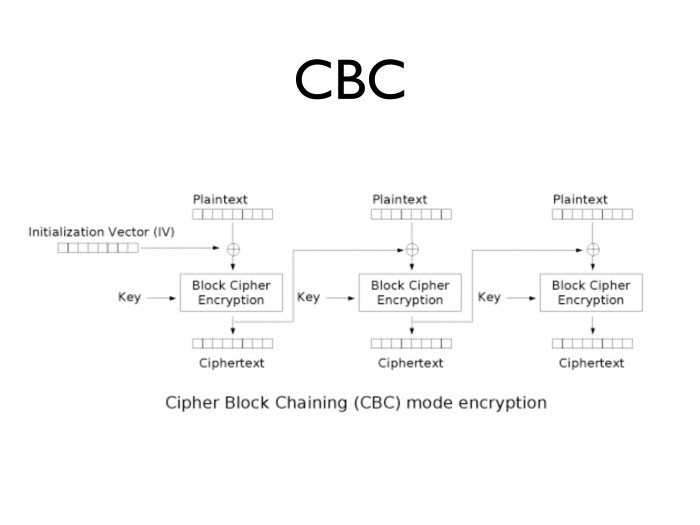
Допустим, мы пронаблюдали коллизию через 30 секунд. Две части равны. Шифрование является взаимно однозначным соответствием. Таким образом, раз функции шифрования равны, то подшифрование тоже равное.
Cj-1 и Ci-1 — их мы видели, ведь они только что передавались в канале связи.
Другими словами, если у нас есть настолько маленький размер блока, то даже при абсолютно стойком шифровании мы спустя некоторое время начнем получать разности между какими-то двумя случайными открытыми текстами. Это свойство необязательно трансформируется в реальную атаку, но на практике оно не очень хорошее. Из-за него режим СВС является причиной многих бед.
Последняя из таких бед — атака (неразборчиво — прим. ред.), опубликованная буквально пару недель назад. Она крайняя, но, думаю, не последняя в этом ряду. И всё из-за злосчастного свойства СВС, о котором я рассказал.
Однако СВС — по-прежнему широко распространенный режим шифрования. Его можно встретить где угодно.
— Если нужно взять последние 10 бит, нам придется считать последовательно…
— Да, конечно, у СВС есть проблема: чтобы расшифровать 1 гигабайт и прочитать в нем последние 10 байт, нужно сначала нагенерировать это всё.
Несмотря на все сложности с СВС, он по-прежнему является самым распространенным режимом шифрования: в TLS точно, но думаю, что и в IPsec — то есть в протоколах, используемых в реальной жизни.
Как с этим в реальной жизни борются? В первую очередь, Triple DES уже широко не используется. Далее, если посмотреть на AES с размером блока 128 бит, то вероятность коллизии ½ наступает примерно после 264 блоков, а это очень много трафика. Поэтому в реальной жизни вероятность, что мы наткнемся на коллизию, невысока. Так что не надо использовать Triple DES и ГОСТ-28147, если вы не государственная организация и не вынуждены их использовать.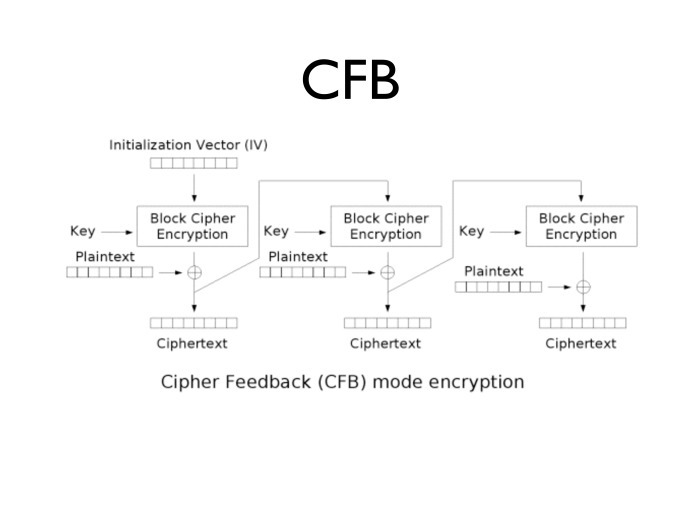
СВС — не единственный режим шифрования. Есть еще CFB. Он, если посмотреть внимательно, сильно от СВС не отличается. Мы берем инициализационный вектор, ксорим с ним открытый текст и получаем шифротекст. Результат шифруем еще раз, ксорим с ним открытый текст, получаем второй блок текста и т. д.
Почему я вообще заговорил про CFB? Потому что, в отличие от СВС, вариант CFB стандартизован для ГОСТа. Если внимательно посмотреть, он в этом смысле ничем не лучше СВС — в нем есть такая же проблема. В закрытых системах можно встретиться с указанной реализацией, с ней в принципе возникают некоторые проблемы.
А какие еще проблемы бывают у этих алгоритмов? Чтобы расшифровать каждый следующий блок, нам нужен зашифрованный открытый текст. Без доступного блока открытого текста мы не можем сгенерировать следующий блок шифрования. Чтобы от этой проблемы избавиться, придумали режим OFB. Он устроен так: дается инициализированный вектор, он шифруется ключом, результат шифруется ключом еще раз, еще раз… Фактически мы берем и шифруем инициализационный вектор много раз — столько, сколько блоков нам нужно.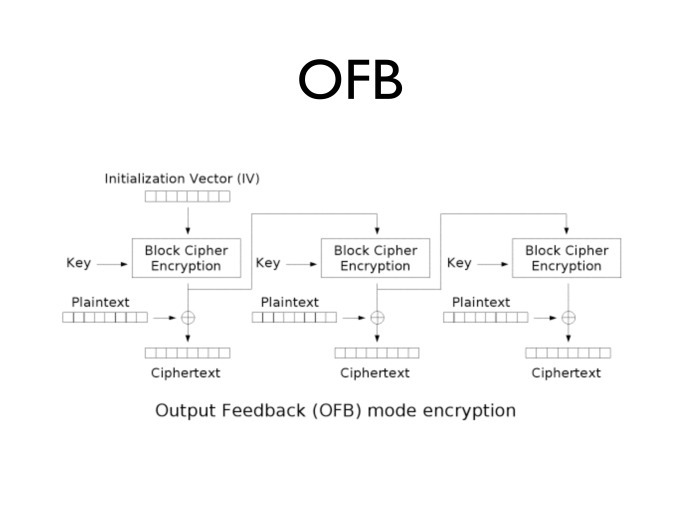
Блоки мы складываем с открытым текстом. Почему это удобно? Если внимательно посмотреть, блочный режим шифрования превращается в потоковый. Если сейчас трафика мало, а процессор свободен, мы можем загодя нагенерировать несколько блоков и затем израсходовать их при возможном всплеске трафика. Очень удобно. И нам не нужно знание открытого текста, чтобы зашифровать следующий блок. Можно набрать и держать несколько гигабайт в памяти — на случай, если понадобятся.
Все недостатки поточных шифров тут тоже присутствуют.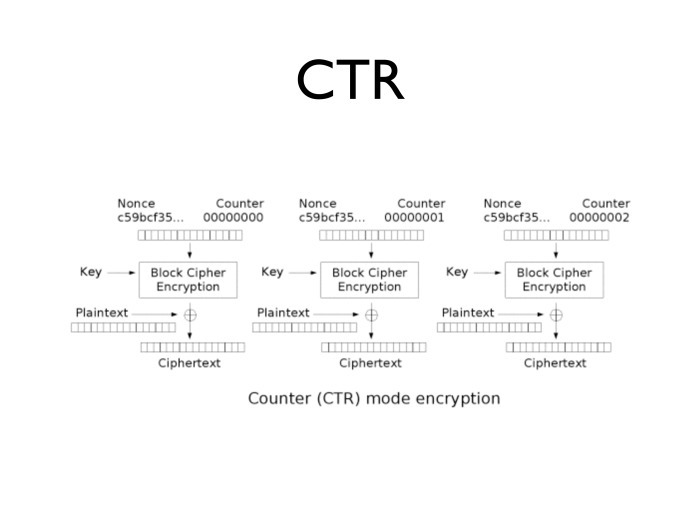
Немного другой способ шифрования — так называемый counter mode или CTR. Он устроен просто: берем некое случайное число, помещаем его в начало блока, а в конец просто помещаем счетчик от нуля до скольки угодно. Например, до 64 бит. Берем и делим пополам: левые 64 бит отдаем под случайное число, а правые 64 бит — под счетчик.
Шифруем каждое такое число и сводим результат с открытым текстом.
Чем удобен CTR? Он позволяет нам зашифровать 125-й блок, не шифруя предыдущие 124 блока, то есть решает проблему расшифровки последних 16 байт из 10-гигабайтного файла. Он достаточно удобный и во всех остальных смыслах. Если говорить про всплеск трафика, можно загодя нагенерировать блоки для шифрования.
Это в случае с сообщениями длиннее одного блока. А что делать, если они короче одного блока? Другими словами, мы хотим зашифровать не 16, а 8 байт.
— Добить до 16.
— А как? Допустим, мы расшифровали некий блок, в конце у которого четыре нуля. Как мы узнаем, что эти четыре нуля добиты нами, а не являются фрагментом наших блоков?
— Перед передачей зашифрованного сообщения сообщить длину в байтах.
— Удобный способ, но он неудобен тем, что вы перед передачей не всегда знаете размер. Если email — знаете, а если нет?
После передачи? Окей, наверное, можно. А где там искать отличия? Надо осуществлять хранение в каком-то отдельном месте. Вопрос — в каком?
— Не в рамках шифрования.
— Если не в рамках шифрования передавать длину сообщения, вы ее будете раскрывать. Думаю, мы ее скрывали.
Добро пожаловать в мой персональный ад, а именно в систему с паддингом. Идея, что надо в конце сообщения написать, какой оно длины, не очень плохая. Важно только придумать способ дополнения блока, который позволит однозначно установить, что этот кусок в конце — дополнение, а не часть данных.
Существует несколько режимов паддинга, и к сожалению, самый распространенный из них обладает несколькими неприятными свойствами.
Мы берем и в конце последнего блока дописываем каждый свободный байт числом свободных байт. Если в конце осталось 3 байта — мы берем и записываем их: 3, 3, 3.
Если длина сообщения приходится ровно на границу, мы дополняем ее еще одним блоком, куда записываем, по-моему, четыре нуля. Не принципиально. Такой способ кодирования всегда однозначный. Мы открываем, узнаём последний байт и, если он не нулевой, понимаем — надо сколько-то байт отсчитать. Фактически, это хитро закодированная длина сообщения. Если же последний байт нулевой, мы можем отбросить блок целиком. И мы знаем, что полный блок никогда не может закончиться нулем: тогда мы бы его дополнили еще одним полностью нулевым блоком.
Если последний блок заканчивается единицей, то он полный и мы обязательно дополним его еще одним блоком.
Казалось бы, нормально. Перед нами рабочий механизм паддинга.
Допустим, мы проводим атаку. У нас есть система Oracle — ее так в криптографии называют. Это не тот Oracle, который делает базы данных. Речь идет о коробке, устройство которой вам неизвестно, но в данном случае она представляет собой алгоритм шифрования или расшифрования. Вы не знаете, какой внутри ключ, хотя он дает вам какой-то ответ. Однако он точно не даст вам ответ о том, правильно или неправильно расшифровалась строчка, которую вы в него засунули.
Итак, у вас есть указанная коробка. При этом вы видели одно сообщение и точно знаете, что оно расшифровалось нормально. Как ни странно, в реальных системах такое сообщение легко получить.
Дальше вы берете сообщение и засылаете его в коробку, поменяв в нем один последний байт. Коробка может вам вернуть два состояния. Либо вы узнаете, что ваша конструкция как-то хорошо расшифровалась, либо — что она не расшифровалась из-за ошибки паддинга.
Как все работает? Ваш программный код пытается что-то расшифровать, расшифровывает и дальше проверяет паддинг в конце. Если паддинг не соответствует стандарту, вы видите »333» или что-то не в порядке, не весь последний блок нулевой, то она скажет вам: «padding error». За счет такой схемы вы довольно простым образом можете перебрать последние байты последнего блока. Например, если у вас используется злосчастный режим СВС, то, разобрав кусок plain-текста, вы сможете понять, что здесь находилось.
Казалось бы, все выглядит довольно безобидно. Но на практике проблема с атаками padding oracle приводила, например, к удаленному выполнению зловредного кода в Windows 2003 где-то в 2008 году.
Почему так происходит? Мы пытаемся что-то расшифровать, не проверив, что поступившее сообщение действительно отправил тот, от кого мы чего-то ждем.
Добро пожаловать в аутентификацию. Всё, о чём мы только что говорили, обеспечивало конфиденциальность сообщения. Используя шифрование, мы отправляем сообщение и можем быть уверены, что никто кроме получателя его не прочитает. Но когда получатель получает сообщение, как он может проверить, что сообщение действительно поступило от отправителя? Для такой проверки существует отдельный набор протоколов аутентификации сообщений. По-английски это называется MAC — message authentication code. 
Какие тут проблемы? Есть проблема в случае с потоковыми алгоритмами шифрования. Допустим, есть сообщение, о котором мы ничего не знаем. Есть гамма, которая каким-то образом нагенерирована. Получается шифротекст. Допустим, шифр абсолютно стойкий и с ним все хорошо. Но представим, что атакующий взял и изменил какой-то бит в сообщении, которое мы получаем. Обнаружим мы ошибку? Очевидно, нет.
Если он поменял нулевой бит на единицу, он непредсказуемым образом изменил открытый текст. Если он в шифротексте поменял единицу на ноль и в оригинальном сообщении в этом месте тоже был ноль, оно поменяется на единицу. Если мы «флипнули» бит в шифротексте, он флипнется и в открытом тексте. И эту проблему нельзя обнаружить средствами одного алгоритма шифрования.
Понятно, что в блочном шифре будет больше проблем, что они накопятся и что вы наверняка столкнетесь с проблемой паддинга, но в целом указанная проблема все еще есть. Само по себе шифрование не обеспечивает аутентификацию сообщения. Нужен отдельный механизм.
Механизм называется МАС. Как он работает? 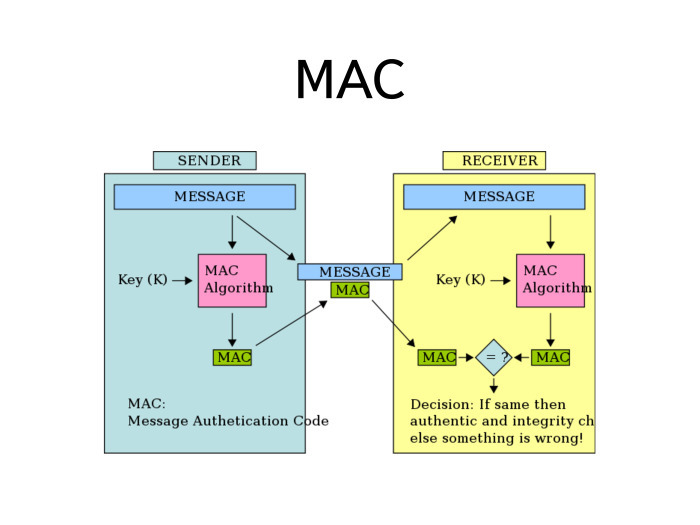
Берем сообщение и пропускаем через специальную функцию под названием МАС-алгоритм. На вход МАС-алгоритм получает не только сообщение, но и ключ, отличающийся от ключа шифрования.
Когда мы хотим передать сообщение, мы прицепляем к нему результат выполнения алгоритма. Получатель берет сообщение, выполняет такую же операцию и сравнивает МАС, который он вычислил, с МАС, который он получил. Если они совпали — значит, сообщение не было изменено в процессе. А если два МАС не совпали, значит, по пути случилась проблема.
Что можно использовать в качестве МАС-функции? Можно использовать количество единиц, но, кажется, такая схема легко форжится.
Хеш-функция — очевидный ответ. А еще?
Долгое время были распространены СВС МАС. Берем конструкцию, в которой нет инициализационного вектора, а все остальное то же самое. Берем шифротекст — шифруем, «чейним», шифруем, «чейним»… Получается последний блок, где накоплена вся информация о нашем тексте. Очень удобно.
Но также совершенно справедливо, что можно использовать какой-нибудь криптографический хеш как элемент МАС. Криптографических хешей существует несколько, самые распространенные из них — MD5, семейство SHA, ГОСТ 34.11… ну и недавно сошелся конкурс на SHA-3, в котором победил алгоритм Keccak.
Хеши устроены сложнее, чем алгоритмы шифрования, но по своему принципу идея построения хеш-функции похожа на алгоритм блочного шифрования. Другими словами, мы берем какой-нибудь блок данных и последовательно, несколько раз применяем к нему набор достаточно примитивных операций. Если посмотреть на MD5, то там есть только сложение по модулю 2 и циклические сдвиги. Применяем их много раз — как правило, гораздо больше, чем в случае с алгоритмами блочного шифрования. Если по пути встречается текст, от которого нам надо взять более длинную, чем один блок, функцию, то мы чейним их при помощи способа, немножко похожего на СВС. Мы добавляем эти фрагменты к нашей вычисляемой функции.
Результатом вычисления хеша является числа. Длина числа всегда фиксированная. Типичные размеры выхода хеша для MD5 — 128 бит, для SHA-1 — 168 бит, для SHA-256 — 256 бит, для SHA-384 — 384 бита, и для SHA-512 — 512 бит.
Что еще важного можно сказать про хеши? При малых изменениях на входе хеш обязан обеспечивать большие изменения на выходе. Значит, если в открытом тексте на входе мы поменяли один бит, то в идеале хеш, результат вычисления хеш-функции, должен измениться ровно наполовину.
Сейчас в реальной практике рекомендуется использовать SHA-2, а конкретно SHA-256 или SHA-384 — в зависимости от ваших потребностей. MD4 поломан давно, MD5 — в принципе, тоже поломан: буквально вчера опубликована новая атака на MD5, где ребята классным образом используют Sony PlayStation для генерации коллизий. Можно считать, что использовать MD5 больше не надо. В реальной жизни всегда используйте SHA-2.
Где еще, помимо аутентификации, применяются хеш-функции? В протоколе выработки ключей, например в PBKDF2. Предположим, вам нужно зашифровать какой-нибудь файл. Вы берете пользователя и, как правило, спрашиваете пароль, с помощью которого надо файл зашифровать. В реальной ситуации пользователь введет в качестве пароля что-то вроде последовательности от 1 до 5, и его работа будет закончена.
С одной стороны, вам хочется, чтобы ваш ключ шифрования был не таким предсказуемым, как »12345», и чтобы распределение бит было более равномерным. С другой — если атакующий начинает перебирать все возможные варианты паролей, каждая атака перебором должна занимать как можно больше времени. Указанный класс KDF-функций нацелен именно на это.
PBKDF2 — конкретная функция из класса функций генерации ключей. Устроена она очень просто. Она только и делает, что применяет алгоритм хеширования несколько десятков тысяч раз. А попутно — на каждом этапе — подмешивает дополнительные данные так, чтобы вычислить ее заранее было довольно тяжело.
Поскольку хеш-функция выполняется довольно долго, то выполнение хеш-функций несколько тысяч раз занимает еще больше времени. Другими словами, мы удобным способом защищены от атакующего, который пытается перебрать несколько распространенных паролей.
В реальной жизни, когда применяется KDF-функция, рекомендуется выбирать количество итераций таким, чтобы оно было, с одной стороны, приемлемым для нетерпеливого пользователя, а с другой — неприемлемым для атакующего, который хочет подобрать несколько миллионов ключей. В реальной жизни подбирайте такое количество итераций в KDF, чтобы оно, например, выполнялось одну секунду. Для атакующего одна секунда — совершенно непристойное время, а вот пользователь, нажимая кнопку и ожидая, пока пароль проверяется, вполне способен одну секунду подождать.
Хранение паролей — то же применение хешей. Антон в рассказе про UNIX обязательно расскажет и об этом.
Поскольку у нас есть атаки padding oracle и похожие, то, когда мы генерируем сообщение, есть два варианта действий.
Есть криптопримитив типа МАС, и есть криптопримитив для шифрования. Мы хотим отправить сообщение и аутентифицировать его. Есть два способа. Мы можем сообщение зашифровать, потом взять МАС от этой штуки и прицепить его к сообщению. Целиком оно будет выглядеть так: E (T) || MAC (E (T)).
Второй способ следующий: берем сообщение, шифруем его и берем МАС от открытого текста. Потому что зачем нам лишняя операция?
По сути, одно называется MAC before encrypt, а второе — encrypt before MAC.
Вопрос — что лучше? Одинаково? Окей, еще версии?
Есть еще один прекрасный способ — мол, давайте зашифруем МАС, чтобы никакое знание про открытый текст точно не утекало.
Действительно, с этим способом есть проблема: если вы с помощью него зашифруете сообщение, то возникнет риск натолкнуться на атаку padding oracle. Padding oracle не беспокоится о том, МАС у вас в конце или какие-то другие данные. У вас будет коробка, которая сначала попытается расшифровать сообщение. Если из-за неправильного паддинга оно не расшифруется, коробка даже МАС не станет проверять, а сразу ответит в сторону атакующего или еще кого-то, что «я не смогла расшифровать эту штуку». Достаточно неприятно. Поэтому вот общая рекомендация к дизайну таких систем — если не знаете, что творите, лучше используйте такую вещь, а если знаете — такую: E (T) || MAC (E (T)).
Буквально полгода назад мы с Антоном дискутировали про одно место, и я настаивал на использовании второй конструкции. Я думал, что знаю, что творю. И мне до сих пор кажется, что я знал, что творил, ведь там не было padding oracle.
Умеем шифровать наше сообщение, умеем проверить, что полученное сообщение действительно пришла от отправителя. Эта конструкция состоит в следующем: A и B заранее договорились о разделяемом секрете, который они потом смогут использовать для шифрования сообщений и их верификации.
В реальной жизни, если есть секрет, разделяемый между двумя персонажами, то он, конечно, никогда не используется в качестве ключа шифрования или ключа проверки подписи. Из него за счет какой-нибудь KDF-функции обязательно будут нагенерированы подключи: ключ шифрования и ключ верификации, которые уже будут использоваться в реальных протоколах. Это не оригинальный разделяемый секрет.
Какая здесь проблема? Когда есть Алиса и Боб — есть один разделяемый ключ. Когда есть три персонажа — есть три разделяемых ключа. Четыре — еще немного. Когда у нас 100 персонажей, то разделяемых ключей очень много. А когда мы Яндекс, у нас 100 млн пользователей, и мы хотим с каждым надежно всё шифровать — проблема становится неподъемной.
Значит, необходим механизм, который позволял бы не хранить десятки миллионов ключей, одновременно обеспечивая надежность шифрования между большим количеством абонентов в группе.
Возникшую проблему долго не удавалось решить — пока не появилась концепция асимметричных шифров.
Чем асимметричный шифр отличается от симметричного? 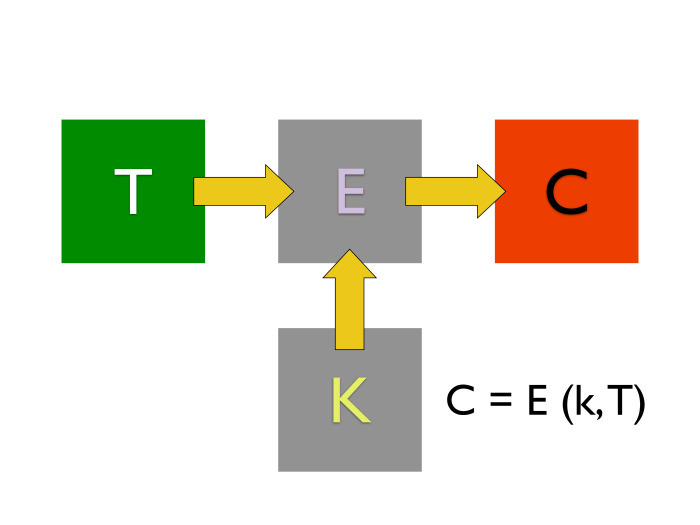
В асиметричном шифре существует два ключа k1 и k2, связанные нетривиальным соотношением. Если некое сообщение зашифровано на ключе k1, то расшифровано оно может быть на ключе k2. Иногда и наоборот, но не всегда.
Важно: k1и k2 в реальной жизни таковы, что, зная один, нельзя вычислить второй. Между ними существует соотношение, но оно нетривиальное.
Причиной, почему такая схема возможна, является существование однонаправленных функций. Речь идет о таких функциях, которые легко вычислить в одну сторону, но без знания какого-то секрета сложно обратить.
Точно неизвестно, существуют ли такие функции в математическом смысле, но если бы они существовали, можно было бы доказать, что P = NP. Сейчас не существует ни одной функции с доказанной обратимостью. Если говорить конкретно про RSA, люди просто верят, что он такой. Эффективных атак тоже пока не существует.
Исторически первыми ребятами, придумавшими нечто похожее на однонаправленные функции, были Диффи и Хеллман. Изобретенный ими алгоритм называется алгоритмом Диффи-Хеллмана (DH). По сути, речь идет о средстве выработки секрета между двумя участниками, которые заранее не общались.
Есть Алиса и Боб. Пусть у них есть общее знание про числа P и G. Это основание поля и генератор.
Алиса генерирует большое случайное число, а и вычисляет генератор в степени a по модулю Р. Результат А она пересылает Бобу.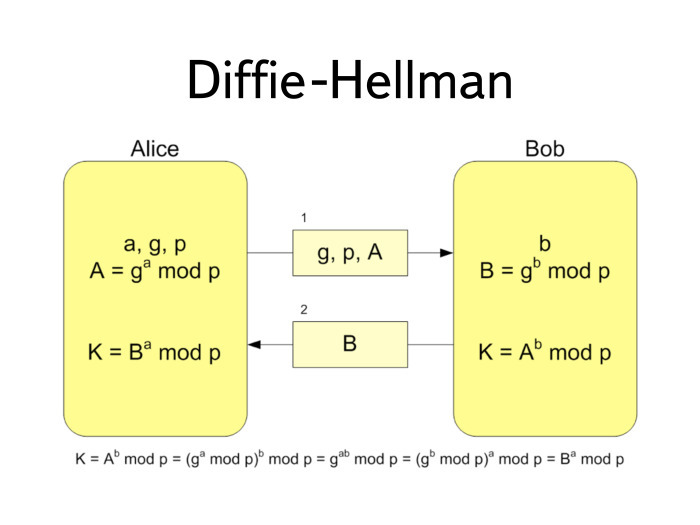
Боб берет какое-то случайное число В, вычисляет тот же самый генератор в степени B по модулю Р. Генератор и модуль G и P представляют собой открытые данные. Если посмотреть на реальные криптографические протоколы, G и P являются свойствами конкретной группы. Про них обычно так прямо и пишут.
Что происходит дальше? Боб вычисляет В и пересылает его Алисе. Алиса берет В и возводит в свою степень а, а Боб берет число, полученное от Алисы, и возводит в степень b. Внизу равенство: Вa = Ab. Не очень сложно.
Таким образом, два участника соединения смогли получить, вычислить некий общий секрет, не передавая его по проводу. Получилось очень удобно.
Кажется, здесь всё здорово в ситуации, если Алиса и Боб изначально знают, когда они разговаривают друг с другом, — что немного сводит эту проблему к точке 0.
Еще лет пять спустя Ривест, Шамир и Адлеман придумали криптосхему, которую назвали в честь себя — RSA. 
Берем два больших случайных числа. Тут написано — 1024 бита. В современных системах бит обычно 2048, 4096 или даже 8192: речь идет про действительно большую, длинную запись.
Вычисляем их произведение — модуль.
Вычисляем значение функции Эйлера от числа (n-1)(p-1). Функция Эйлера — количество натуральных чисел, взаимно простых с аргументом функции и меньше указанного аргумента.
Если посмотреть на функцию Эйлера, она выглядит примерно так: растет, растет и падает. На графике сколько-то лучей. Функция Эйлера имеет излом в каждой точке.
Дальше вычисляем взаимно простое с функцией Эйлера число е и еще одно число — мультипликативно обратное числу е по модулю. Оно такое, что на этом модуле функции Эйлера произведение двух полученных чисел равно единице.
Числе е мы называем публичной экспонентой, а d — секретной экспонентой. Последняя вычисляется при помощи алгоритма Евклида как наименьшее общее. В школе, классе в третьем, мы все проходили вычисление наибольшего общего и наименьшего общего. Вот почему не надо рассказывать про математику RSA.
Важно, что мы выбрали два таких числа, что по указанному модулю их произведение равно единице. Иначе говоря, одно число представимо как единица плюс некое k, умноженное на функцию Эйлера, где k — целое число.

Дальше, когда мы хотим что-то зашифровать, мы представляем это что-то в виде числа, которое мы возводим в степень е по вычисленному нами основанию n. Результат возведения в степень как раз и является шифротекстом. Такая операция гораздо сложнее, чем любые операции в симметричных алгоритмах шифрования, но принципиально несложная.
Если мы хотим расшифровать наше что-то, мы возводим его в степень d.
А поскольку de = 1 по модулю функции Эйлера от n, то результат, Med mod n, означает, что это M1 по модулю n. Таким образом и происходит расшифровка. M1 = M.
Если есть такой классный алгоритм шифрования как RSA, то почему бы не шифровать им всё подряд? Мы берем два ключа, k1 и k2, один называем публичным, другой — секретным. В данном случае е — публичный ключ, d — секретный. Всё, что мы зашифровали на публичном ключе, мы можем расшифровать на секретном, а всё, что мы зашифровали на секретном ключе, можно расшифровать публично. Здесь наблюдается симметрия: можно Me сделать, а потом в степени d, или Md, а потом в степени е.
Если есть такой классный алгоритм шифрования как RSA, то зачем мы вообще пользуемся симметричными алгоритмами?
Конечно, из-за скорости. Симметричные алгоритмы состоят из XOR и сдвигов, ну и еще из подстановок в таблицах. На процессорах все указанные операции выполняются, как правило, одной ассемблерной командой. Вот почему симметричные алгоритмы шифрования очень быстрые. Здесь же надо выполнить операцию возведения в степень — намного более дорогую, и ее производительность намного ниже, чем производительность любого симметричного шифра.
Есть и вторая проблема. Мы поняли, как с помощью симметричных шифров шифровать куски длиной больше, чем блок произвольной длины. А с RSA мы не можем шифровать куски произвольной длины, поскольку возведение в степень — дорогая операция. Нельзя зашифровать что угодно. Поэтому в реальной жизни делается иначе: когда мы хотим отправить кому-то сообщение, мы можем как-нибудь выработать сеансовый ключ с помощью ассиметричного шифрования, а потом с помощью полученного ключа начать выполнять шифрование потока данных, используя симметричный алгоритм и классические МАС-функции.
RSA использует ключи длиной 1024, 2048, 4096 бит — довольно большие. Алгоритмы симметричного шифрования AES, DES и Salsa используют следующие длины ключей: 256, 128 бит или даже 64 в случае с DES.
Вопрос, какой ключ более стойкий — RSA-2048 или AES-256? В RSA числа очень большие, но вы же понимаете, что в AES ключом может служить полный набор из всех 2256 вариантов, а в RSA — далеко не каждое число. В первую очередь мы берем случайные простые числа, которые даже среди больших чисел встречаются далеко не подряд. Вариантов ключей в пространстве 22048 намного меньше. 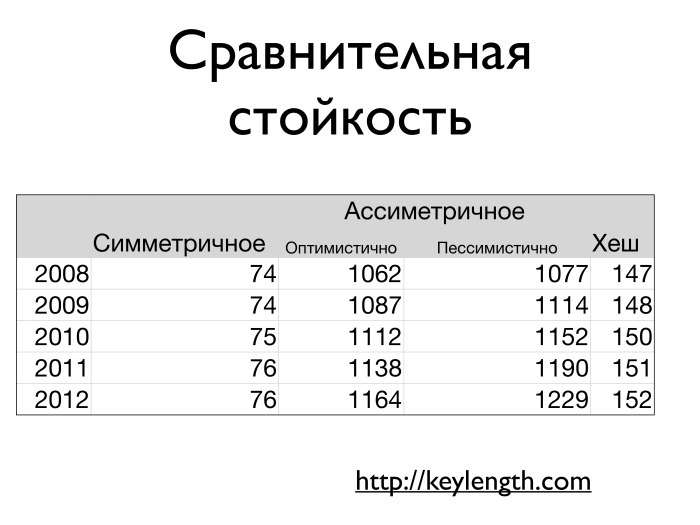
Нет математической теоремы, где говорилось бы, что такая-то длина ключа соответствует такой-то длине ключа из другого алгоритма. Существует некий эмпирический набор представлений о том, что чему соответствует. Есть критерий Ленстры, основанный на примерном времени, которое требуется для подбора ключа при атаке полным перебором. И считается, что это примерно характеризует пространство ключей в некой области.
Критерий Ленстры где-то там закончился, но такие таблицы есть и для нынешних дат. Можно сказать, что 2014 году соответствует AES с ключом длиной примерно 78–80 бит. Эквивалентный ему симметричный алгоритм шифрования, а конкретно RSA, работает при длине 1300–1400 бит. Можно зайти на keylength.com и посмотреть, сколько там сейчас. Разумная длина хеша сейчас — 160–170 бит. То есть SHA1 в 2014 году уже не применим просто с точки зрения атаки полным перебором, поскольку длина его выхода — 168 бит.
Когда вы дизайните какую-нибудь криптосистему, необходимо соблюдать баланс между длинами ключей, симметричным и асимметричным алгоритмом шифрования и длиной хеша.
Мы выучили три примитива. Давайте посмотрим, как, используя их, полностью зашифровать сообщение и переслать его от одного пользователя другому.
Давайте разберем два варианта. Первый вариант: два пользователя находятся онлайн и могут быстро обмениваться друг с другом сообщениями. Второй: пользователи не находятся онлайн и обмениваются сообщениями с некоторой задержкой. Давайте посмотрим, как можно эффективно реализовать обмен в обоих случаях.
Начнем со второго случая. Грубо говоря, это email. Что делать, если мы хотим отправить сообщение от Алисы Бобу?
Алиса генерирует симметричный ключ — допустим, длиной 128 бит. Что еще есть? Сразу скажем, что у Алисы есть публичный ключ Боба. У нее есть свой публичный ключ и есть свой приватный ключ.
У Боба есть его публичный ключ, публичный ключ Алисы и свой приватный ключ.
Мы говорили, что Алиса не может зашифровать сообщение публичным ключом Боба, потому что оно может быть длиной в несколько гигабайт, а возвести число в степень нескольких гигабайт мы не можем.
Симметричный ключ шифруется ключом Боба.
Мы шифруем сообщение симметричным алгоритмом на этом ключе. Вычисляем хеш. Берем сообщение, зашифрованное на ключе, сгенерированном случайно при помощи какого-нибудь симметричного алгоритма. К указанному сообщению мы пристыковали хеш, зашифрованный на приватном ключе Алисы.
Ключ шифруем на публичном ключе Боба.
Мы сгенерировали случайное 128-битное число, которое стало нашим сеансовым ключом. С помощью этого 128-битного ключа, используя симметричный алгоритм, мы зашифровали сообщение. Мы взяли хеш от сообщения, зашифровали его на нашем приватном ключе. еще мы взяли наш сессионный ключ и зашифровали его на публичном ключе Боба. Затем мы сконкатинировали все три конструкции и отправили результат Бобу.
Каковы действия Боба? Сначала он расшифровывает сессионный ключ, используя свой приватный ключ. Поскольку он зашифрован на публичном ключе Боба, то его можно расшифровать только с помощью приватного ключа Боба. Боб получил сессионный ключ, дальше публичным ключом проверяет, что письмо пришло от Алисы… Или все-таки сначала расшифровывает сообщение?
Есть версия, что необходимо подписывать и брать хеш от зашифрованного сообщения. А здесь мы берем хеш от открытого текста. Так как лучше делать?
С другой стороны, если мы считаем, что за нами наблюдает всевидящее око АНБ… Это ряд, о котором я уже рассказывал. Только я о нем рассказывал применительно к padding oracle, что очень актуально для онлайновых атак, а здесь ситуация офлайновая, и он не всегда очевиден.
Что делает Боб? Боб видит блок, который, предположительно, зашифрован на приватном ключе Алисы. Он может использовать публичный ключ Алисы, чтобы расшифровать указанный фрагмент. Расшифровав его, Боб получит либо хеш от сообщения, либо хеш от зашифрованного сообщения — в зависимости от того, что именно мы зашифровали.
Дальше Боб вычисляет на своей стороне хеш либо от зашифрованного сообщения, либо от сообщения, которое он зашифровал с помощью сессионного ключа. Боб может сравнить вычисленный и полученный хеши: если они совпали, значит, сообщение дошло. Во-первых, оно не изменилось в процессе — свойство хеша это гарантирует. Во-вторых, поскольку он смог расшифровать указанный фрагмент на публичном ключе Алисы, то сообщение действительно пришло от нее.
Какой здесь тонкий момент? В области, где надо либо расшифровать и потом проверить, либо подписать и потом зашифровать.
Речь идет об офлайновой коммуникации. Примерно так, если не углубляться в детали, устроены S/MIME и PGP. Обо всех остальных деталях, связанных с пониманием, что ключ действительно от Алисы, завтра расскажет Антон.
Снова есть Алиса, которая хочет отослать сообщение Бобу. Она знает публичный ключ Боба, свой публичный ключ и свой приватный ключ. И есть Боб, который знает свой публичный ключ, публичный ключ Алисы и свой приватный ключ. Допустим, они оба онлайн. Что мы можем здесь сделать? В чем разница?
Важное отличие: когда оба абонента находятся онлайн, мы имеем возможность сделать DH и, таким образом, выработать сеансовый ключ. Дальше задача сводится к предыдущей.
Если они оба онлайн, и сначала мы можем произвести полноценный DH, то, произведя его, мы на обеих сторонах получим общий ключ.
Проблема с DH состоит в атаке посередине (англ. man-in-the-middle или MITM — прим. ред.). Другими словами, отправляя и посылая результат возведения в степень, мы на самом деле не знаем, кому мы его отправили и от кого получили. Если у нас есть человек, находящийся посередине между Алисой и Бобом, он может получить от Алисы какое-нибудь число, нагенерировать свое число, послать его Бобу от имени Алисы, получить от Боба новое число, сгенерировать еще какое-нибудь число и послать его Алисе от имени Боба. Вместо одной DH-сессии будут две — со злоумышленником посередине. Но ни Алиса, ни Боб не смогут проверить, что они разговаривают друг с другом напрямую.
Что делать? Подписывать ключами, которые есть.
— На одной стороне эти параметры шифруются приватным ключом, на другой — расшифровываются…
— Алиса вот так посылает? А какая польза?
— Только Боб сможет расшифровать…
— Почему? Кто угодно сможет расшифровать.
— Сообщение шифруется публичным ключом Боба, чтобы расшифровать его своим приватным ключом мог только Боб.
— Любой желающий в интернете сможет зашифровать сообщение публичным ключом Боба. Как Боб проверит, что сообщение пришло от Алисы?
— …и подписать приватным ключом Алисы.
— А зачем шифровать? Я рассказывал, что у DH есть очень удобное свойство: наблюдающий, даже если он видит весь обмен, не может восстановить сессионный ключ.
— Чтобы нельзя было наладить две DH-сессии и устроить MITM?
— Нет. Что атакующий получает, если видит DH-сессию? Я же сказал, что сессионный ключ в DH-сессии он установить не может. MITM может, и для этого нужно шифрование? Не верю.
Какой механизм нужен, чтобы проверить аутентичность полученного сообщения? Подпись. Алиса генерирует А, берет х
