Восстановление таблиц Хаффмана в Intel ME 11.x06.12.2017 16:03

Сегодня эксперт Positive Technologies Дмитрий Скляров на конференции Black Hat в Лондоне расскажет о том, как устроена файловая система на которой располагается часть Intel CSME / ME версий 11.x и некоторые файлы для этой системы. Мы представляем вашему вниманию его статью о восстановлении таблиц Хаффмана в Intel ME 11.x.

Как известно, многие модули Intel ME 11.x хранятся во Flash-памяти в упакованном виде, и для сжатия применяются два алгоритма — LZMA и Huffman Encoding. Для LZMА существует публичная реализация, которую можно использовать для распаковки, но для Huffman все сложнее. Распаковщик Huffman Encoding в ME реализован на аппаратном уровне, и построение эквивалентного программного кода представляет собой сложную и нестандартную задачу.

Предыдущие версии ME

Ознакомившись с исходными текстами, являющимися частью проекта unhuffme, легко увидеть, что для предыдущих версий ME существует два набора таблиц Хаффмана и в каждом из наборов присутствует две таблицы. Наличие двух таблиц (по одной для кода и для данных) обусловлено, вероятно, тем, что статистические свойства кода и данных сильно отличаются.

Также примечательны следующие свойства:

Для разных наборов таблиц диапазоны длин кодовых слов различаются (7–19 и 7–15 бит включительно).
Каждая кодовая последовательность кодирует целое количество байт (от 1 до 15 включительно).
В обоих наборах используется Canonical Huffman Coding (это позволяет быстро определять длину очередного кодового слова при распаковке).
В пределах одного набора длины закодированных значений для любого кодового слова совпадают во всех таблицах (Code и Data).

Постановка задачи

Можно предположить, что в таблицах Хаффмана для ME 11.x три последних свойства также соблюдаются. Тогда для полного восстановления таблиц требуется найти следующее:

диапазон длин кодовых слов;
границы значений кодовых слов, имеющих одинаковую длину (Shape);
длины закодированных последовательностей для каждого кодового слова;
закодированные значения для каждого кодового слова в обеих таблицах.

Разбиение сжатых данных на отдельные страницы

Для получения информации об отдельных модулях можно использовать имеющиеся знания о внутренних структурах прошивки.

Разобрав Lookup Table, являющуюся частью Code Partition Directory, легко определить, для каких модулей применяется кодирование Хаффмана, где начинаются их упакованные данные и какой размер модуль будет иметь после распаковки.

Разобрав Module Attributes Extension для конкретного модуля, несложно найти размер сжатых и распакованных данных и SHA256 от распакованных данных.

Бегло проанализировав несколько прошивок для ME 11.x, легко заметить, что размер данных после распаковки Хаффманом всегда кратен размеру страницы (4096 == 0×1000 байт). В начале упакованных данных располагается массив четырехбайтовых целочисленных значений. Количество элементов массива соответствует количеству страниц в распакованных данных.
Например, для модуля размером 81920 == 0×14000 байт массив будет занимать 80 == 0×50 байт и состоять из 20 == 0×14 элементов.

В двух старших битах каждого из Little-Endian-значений хранится номер таблицы (0b01 для кода и 0b11 для данных). В оставшихся 30 битах хранится смещение начала сжатой страницы относительно конца массива смещений. Приведенный выше фрагмент описывает 20 страниц:

Примечательно, что смещения упакованных данных для каждой страницы отсортированы по возрастанию, а размер упакованных данных для каждой страницы в явном виде нигде не фигурирует. В приведенном выше примере упакованные данные для каждой конкретной страницы начинаются на границе кратной 64 = 0×40 байтам, а неиспользуемые области заполнены нулями. Но по другим модулям можно установить, что наличие выравнивания не является обязательным. Это наталкивает на мысль, что распаковщик останавливается, когда объем данных распакованной страницы достигает 4096 байт.

Так как мы знаем общий размер упакованного модуля (из Module Attributes Extension), мы можем разделить упакованные данные на отдельные страницы и работать с каждой страницей отдельно. Начало упакованный страницы определяется из массива смещений, а размер — смещением начала следующей страницы или общим размером модуля. При этом после упакованных данных может идти произвольное количество незначащих бит (эти биты могут иметь любые значения, но на практике они обычно нулевые).

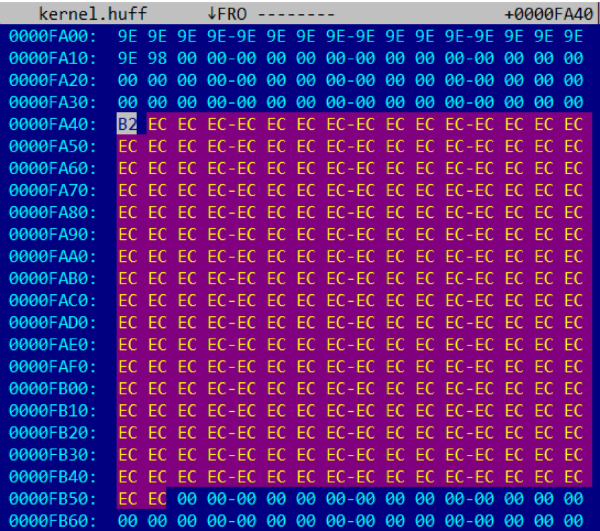
На скриншоте видно, что последняя сжатая страница (начинающаяся по смещению 0xFA40) состоит из байта 0xB2 == 0b10110010, за которым идет 273 байта со значением 0xEC == 0b11101100, и дальше — только нули. Так как битовая последовательность 11101100 (или 01110110) повторяется 273 раза, можно предположить, что она кодирует 4096/273 == 15 одинаковых байт (скорее всего со значениями 0×00 или 0xFF). Тогда битовая последовательность 10110010 (или 1011001) кодирует 4096–273×15 == 1 байт.

Это хорошо согласуется с предположением о том, что каждая кодовая последовательность кодирует целое количество байт (от 1 до 15 включительно). Однако полностью восстановить таблицы Хаффмана таким образом невозможно.

Нахождение пар «сжатый текст — открытый текст»

Как было показано ранее, в разных версиях прошивок для ME 11 модули с одинаковыми названиями могут упаковываться разными алгоритмами. Если разобрать Module Attributes Extension для одноименных модулей, упакованных как LZMA так и Хаффманом, и извлечь значения SHA256 для каждого модуля, — то не обнаружится ни одной пары модулей, упакованных разными алгоритмами и имеющих одинаковые значения хешей.

Но если вспомнить, что для модулей, упакованных LZMA, SHA256 обычно считается от сжатых данных, и посчитать SHA256 для модулей после распаковки LZMA, — обнаружится достаточно много подходящих пар. И для каждого такого «парного» модуля мы сразу получим несколько пар страниц — в упакованном Хаффманом и распакованном виде.

Shape, Length, Value

Наличие большого набора страниц в сжатом и открытом виде (раздельно для кода и данных) позволяет восстановить все кодовые последовательности, используемые в этих страницах. Решение задачи находится на стыке методов линейной алгебры и поисковой оптимизации. Наверное, можно построить строгую математическую модель, учитывающую все ограничения, но так как задача разовая, быстрее оказалось часть работы выполнить вручную, а часть автоматизировать.

Самое важное — хотя бы примерно определить Shape (точки изменения длин кодовых последовательностей). Например, что 7-битовые последовательности имеют значения от 1111111 до 1110111, 8-битовые от 11101101 до 10100011, и т. д. Так как используется Canonical Huffman Coding, знание Shape позволяет определить длину следующей кодовой последовательности (самая короткая последовательность состоит только из единиц, самая длинная — только из нулей, и чем меньше значение, тем длиннее последовательность).

Так как мы не знаем точный размер сжатых данных, можно выкинуть из «хвоста» все последовательности, состоящие только из нулевых бит (так как они самые длинные, и появление самой редкой кодовой последовательности в последней позиции маловероятно).

Когда каждая сжатая страница может быть представлена в виде набора кодовых последовательностей, можно приступать к определению длин кодируемых ими значений. Сумма длин закодированных значений для каждой страницы должна составлять 4096 байт. Это позволяет составить систему линейных уравнений, где неизвестными будут длины закодированных значений, коэффициентами — количество вхождений соответствующей кодовой последовательности в сжатую страницу, а на месте свободного члена всегда стоит 4096. Страницы кода и данных можно обрабатывать совместно, так как для одинаковых кодовых последовательностей длины закодированных значений должны совпасть.

При наличии достаточного количество страниц (и уравнений) единственное решение системы легко находится методом Гаусса. А имея открытый текст, зная длину каждого значения и порядок их следования, несложно получить соответствие кодовых последовательностей и кодируемых ими значений.

Неизвестные последовательности

После обработки всех доступных «парных» страниц получится выяснить значения примерно для 70% последовательностей из кодовой таблицы и 68% последовательностей из таблицы данных. Длины будут известны примерно для 92% последовательностей. И останется некоторая неопределенность в Shape: в некоторых местах может использоваться или одно значение меньшей длины или два значения большей длины, и определить границу невозможно, пока одно из значений не встретится в упакованных данных.

Теперь можно приступать к восстановлению значений для кодовых последовательностей, встречающихся только в модулях, для которых нет открытых текстов.

Если встречается последовательность с неизвестной длиной, в систему уравнений добавляется еще одна строка, и это позволяет быстро определить длину. Но как определить значение, не имея открытого текста?

Верификатор и brute-force

К счастью, в метаданных хранится SHA256 от распакованного модуля. И если мы правильно угадаем значение всех неизвестных кодовых последовательностей во всех страницах, составляющих модуль, вычисленное значение SHA256 должно совпасть со значением SHA256 из Module Attributes Extension.

Когда суммарная длина неизвестных последовательностей составляет 1 или 2 байта, неизвестные байты элементарно находятся лобовым перебором. Так же можно поступать с 3 и даже 4 неизвестными байтами (особенно если они расположены близко к концу модуля), но перебор может занять от нескольких часов до нескольких дней на одном ядре (легко распараллелить на несколько ядер или машин). Попытки перебора 5 и более байт не предпринимались.

Таким образом удается восстановить еще несколько кодовых последовательностей (и несколько модулей). Но потом остаются только модули, в которых суммарный объем неизвестных байт превышает возможности brute-force-подбора.

Эвристики

Однако наличие большого числа модулей, незначительно отличающихся друг от друга, позволяет применять различные эвристики и с их помощью находить значения неизвестных кодовых последовательностей.

Использование второй таблицы Хаффмана

Так как в распаковщике имеется две таблицы Хаффмана, компрессор пытается сжать данные каждой из них, и оставляет ту версию, которая занимает меньше места. Вследствие этого деление на «код» и «данные» оказывается условным. И при изменении части страницы более эффективной может оказаться другая таблица. То есть, посмотрев в другие версии того же модуля, можно найти идентичные фрагменты, которые были упакованы другой таблицей, и так восстановить неизвестные байты.

Многократное использование

Когда одна кодовая последовательность много раз встречается в одном (или разных) модулях (например, в коде и в данных), зачастую легко определить, какие ограничения накладываются на неизвестные значения.

Константы и таблицы со смещениями

В области данных модулей довольно часто встречаются константы и смещения (например, до текстовых строк или функций). Константы могут быть общими и для разных модулей (например, для функций хеширования и алгоритмов шифрования), а смещения уникальны для каждой версии модуля, но должны ссылаться на одни и те же (или очень похожие) фрагменты данных или кода. И их значения очень легко восстановить.

Строковые константы из открытых библиотек

Некоторые фрагменты кода ME явно были позаимствованы из open-source-проектов (например, wpa_supplicant), и фрагменты текстовых строк легко угадываются по контексту и путем подглядывания в исходники.

Код из открытых библиотек

Подсмотрев в исходники и найдя текст функции, для скомпилированного кода которой неизвестно несколько байт, можно поработать компилятором и угадать, какие значения подходят в этом месте.

Сходимость процесса

Начиная с модулей, в которых было меньше всего неизвестных последовательностей, и комбинируя различные эвристики, удавалось шаг за шагом увеличивать известную часть таблиц Хаффмана (каждый раз проверяя правильность предположений вычисляя SHA256). С ростом покрытия модули, где изначально число неизвестных последовательностей измерялось десятками, оказывались не столь пугающими. Процесс выглядел сходящимся, но все уперлось в amt.

Этот модуль самый большой по размеру (порядка 2 мегабайт, примерно 30% от общего объема), содержит множество кодовых последовательностей, которые не встречаются ни в одном другом модуле, но встречаются во всех версиях amt. Можно с высокой вероятностью угадать несколько последовательностей, но единственный способ проверить предположение — угадать их все (чтобы совпало SHA256). Благодаря неоценимой помощи Максима Горячего нам удалось преодолеть и этот барьер, вследствие чего мы получили возможность распаковывать любой из модулей, содержащийся в имеющихся у нас прошивках и упакованный алгоритмом Хаффмана.

Со временем появлялись новые прошивки, и в них попадались не встреченные ранее кодовые слова. Но всякий раз одна из эвристик срабатывала, модуль успешно распаковывался и увеличивалось покрытие таблиц.

Финальный штрих

К середине июня 2017 года мы смогли восстановить примерно 89,4% последовательностей для кодовой таблицы и 86,4% последовательностей для таблицы данных. Но шансы построить за разумное время 100% покрытие таблиц через анализ новых модулей весьма слабы.

19 июня на GitHub пользователем с ником IllegalArgument были опубликованы фрагменты таблиц Хаффмана, покрывающих 80,8% последовательностей для кодовой таблицы и 78,1% последовательностей для таблицы данных. Вероятно, автор (или авторы) использовали аналогичный подход, основанный на анализе имеющихся прошивок. И в опубликованных таблицах не оказалось ничего нового.

А 17 июля Марк Ермолов и Максим Горячий получили возможность узнавать распакованные значения для любых сжатых данных. Мы подготовили 4 сжатых страницы (по две для кода и для данных), и восстановили все 1519 последовательностей для обеих таблиц.

При этом обнаружилось одно непонятное место. В таблице Хаффмана для данных значение 00410E088502420D05 соответствует как последовательности 10100111 (длиной 8 бит), так и последовательности 000100101001 (длиной 12 бит). Это явная избыточность, но скорее всего она обусловлена случайной ошибкой.

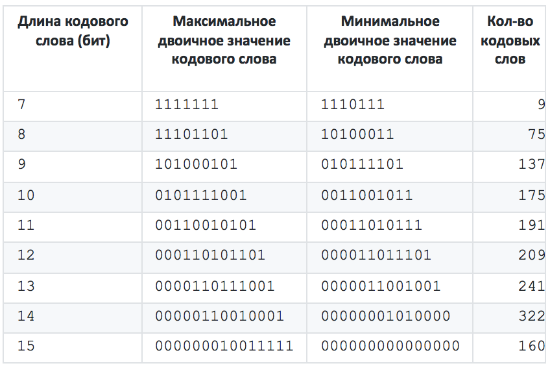
Итоговый Shape имеет следующий вид:

Автор: Дмитрий Скляров, Positive Technologies