Волновые процессы в гидравлических линиях. Основы16.11.2018 12:02

Привет, Хабр!

В предыдущей статье я рассказывал про метод характеристик, предназначенный для расчёта волновых процессов в гидравлических линиях. На самом деле, конечно же, волновые процессы можно рассчитывать и в уме, нужно только знать подход.

Под катом я покажу «на пальцах» и при помощи гифок основные волновые эффекты. В качестве примера я буду использовать опять гидравлическую линию, но на самом деле в основе лежат практически те же самые уравнения, что и для акустики и электрических линий. Так что, даже если вы не гидравлик, может быть простые аналогии помогут вам разобраться в волновых процессах в целом.

Осторожно! Под катом 15 Мб анимированных гифок!

Итак, здесь мы будем рассматривать распространение одномерных плоских волн в гидравлической линии. Это допущение вполне справедливо для длинных трубопроводов, чья длина во много раз превосходит внутренний диаметр. Трением для простоты пока тоже пренебрежём. В этом случае протекающие физические процессы будут описываться парой дифференциальных уравнений в частных производных:

$\frac{\partial p}{\partial t}+\rho\;c^2\frac{\partial v}{\partial x}=0$

$\frac{\partial v}{\partial t}+\frac1\rho\frac{\displaystyle\partial p}{\displaystyle\partial x}=0$

где $\rho$ — плотность, $v$ — скорость, $p$ — давление, $c$ — скорость звука.

С непривычки вид этих уравнений может испугать, но на самом деле здесь всё просто. Первое уравнение говорит нам, что давление будет расти со временем, если в сегмент трубы будет втекать больше жидкости, чем вытекать (при том, тем быстрее, чем более плотная и упругая жидкость находится в трубе); второе уравнение показывает, что для того, чтобы ускорить сегмент жидкости, нужно приложить к нему разницу давлений (причём, чем больше будет плотность, тем больше нужно приложить разницу давлений, чтобы разогнать сегмент). Т.е. описываются вполне банальные вещи: жидкость сжимаема, жидкость имеет массу.
Оставим аналитическое решение этих уравнений для будущих статей, перейдём сразу к примеру «на пальцах».
Возьмём трубу, заполненную водой, в которой поддерживается давление 100 бар (10 МПа) и протекает расход 30 л/мин. Если на левый конец подать ступеньку давления, она предсказуемо начнёт перемещаться по потоку со скоростью, равной скорости звука в среде.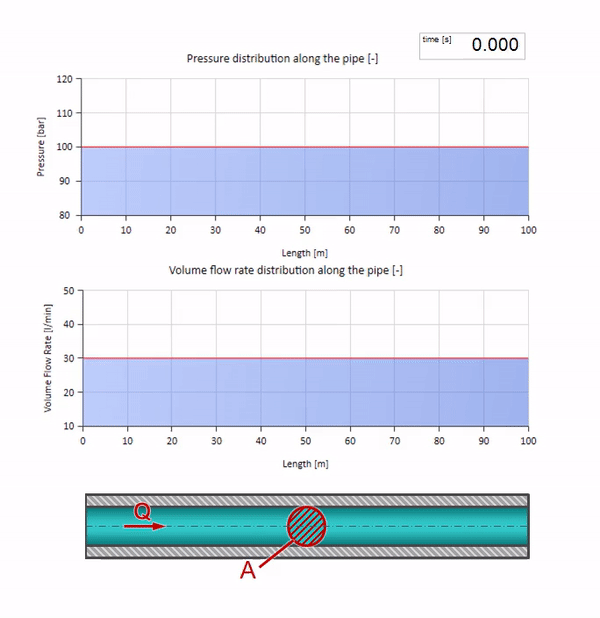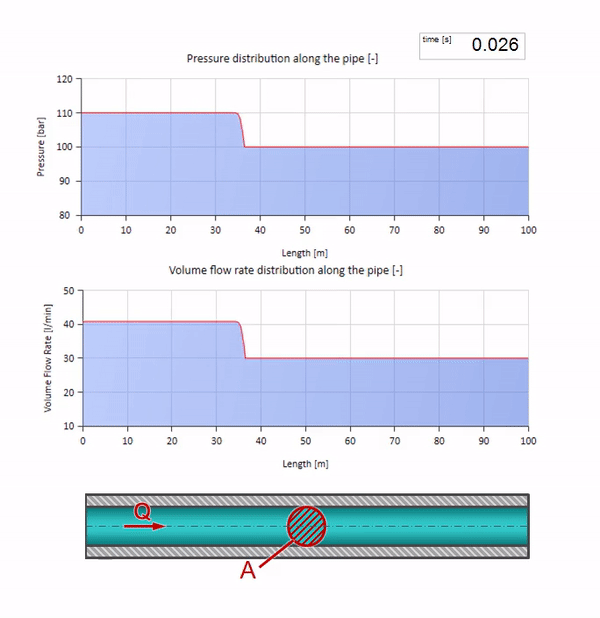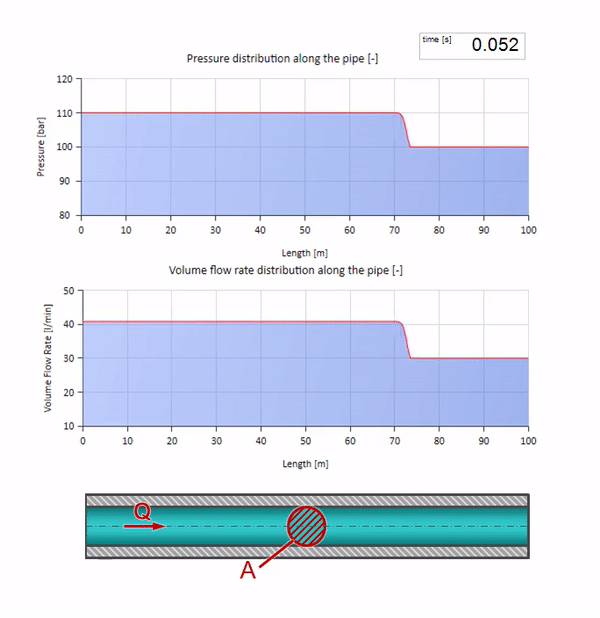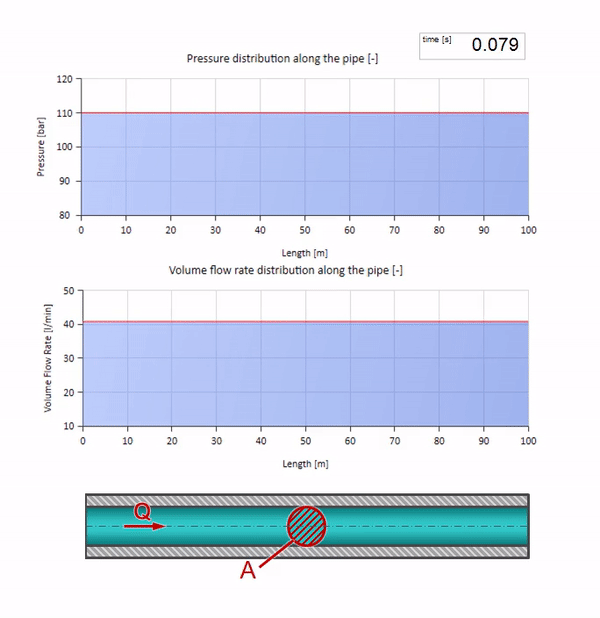

Разумеется, вместе с давлением будет меняться и значение расхода. Если давление растёт, оно будет «подгонять» жидкость по потоку и увеличивать расход тоже на какую-то «ступеньку». Насколько именно, определяется значением волнового сопротивления. Для трубы площадью поперечного сечения $A$ , заполненной жидкостью с плотностью $\rho$ и местной скоростью звука $c$ , волновое сопротивление можно посчитать следующим образом:

$Z_L=\frac{\rho\;c}A$

По размерности это то же самое, что и обычное гидравлическое сопротивление, только используется для расчёта соотношений волн давления ( $\widehat p$ ) и расхода ( $\widehat Q$ ), а не их абсолютных величин:

$Z_L=\frac{\widehat p}{\widehat Q}$

Чем больше плотность и скорость звука, тем выше будет волновое сопротивление, т.е. тем труднее будет определённому перепаду давления разгонять жидкость (увеличивать расход)

Посмотрим теперь как будут вести себя две волны, двигающиеся навстречу друг другу: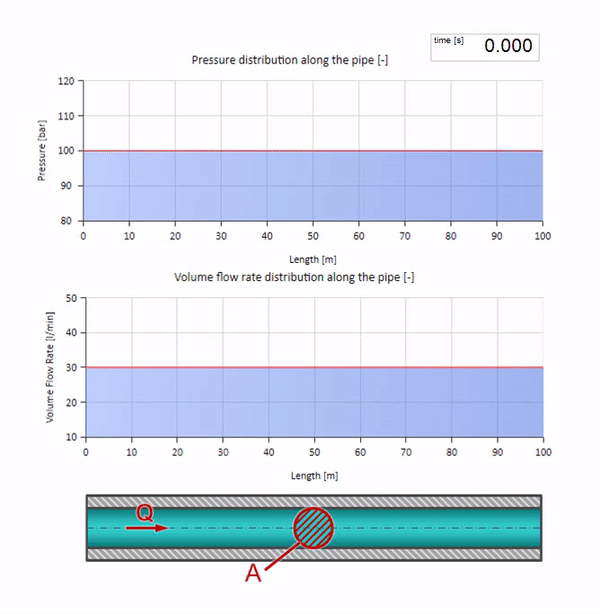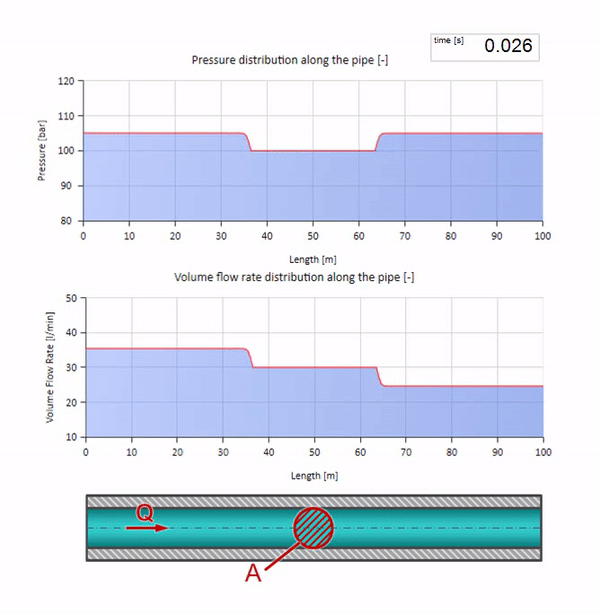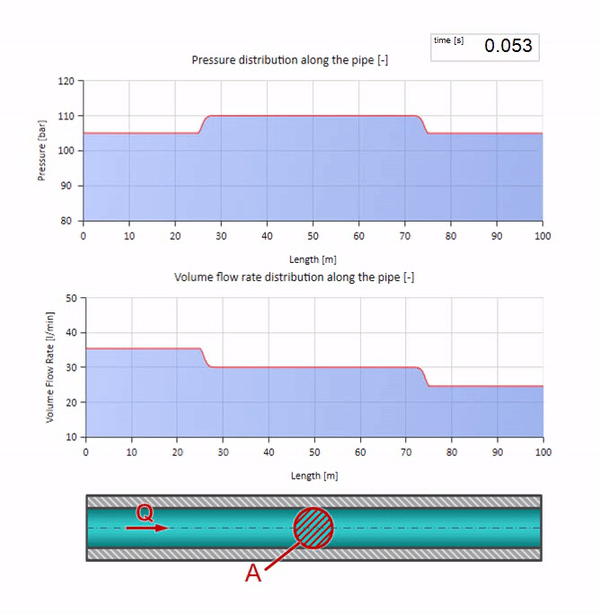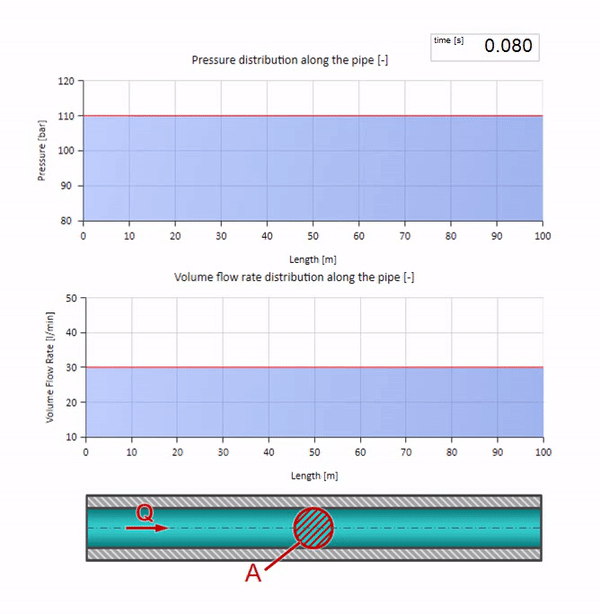

Если давление на правом конце повышается, жидкость неизбежно будет затормаживаться отрицательным перепадом. Значит волна повышения давления, идущая против потока, будет приводить к уменьшению расхода на величину, определяемую опять же волновым сопротивлением. То есть справа будет двигаться волна роста давления и падения расхода.
При столкновении может показаться, что волны расхода отражаются друг от друга и идут обратно. На самом деле они просто накладываются друг на друга. Этот эффект ещё называется интерференцией: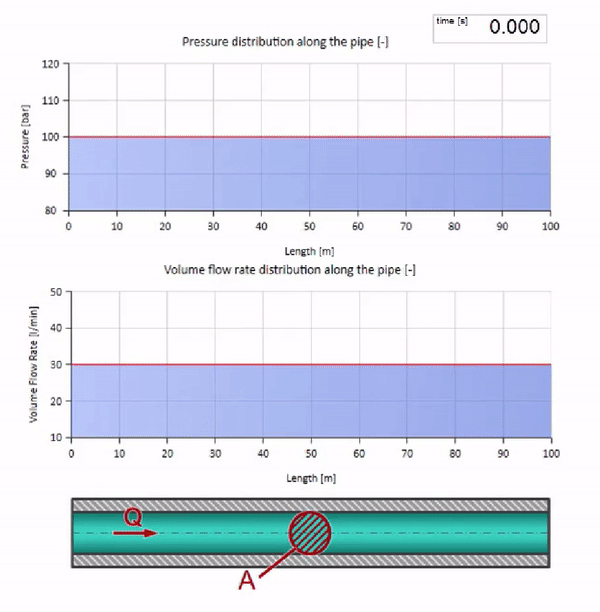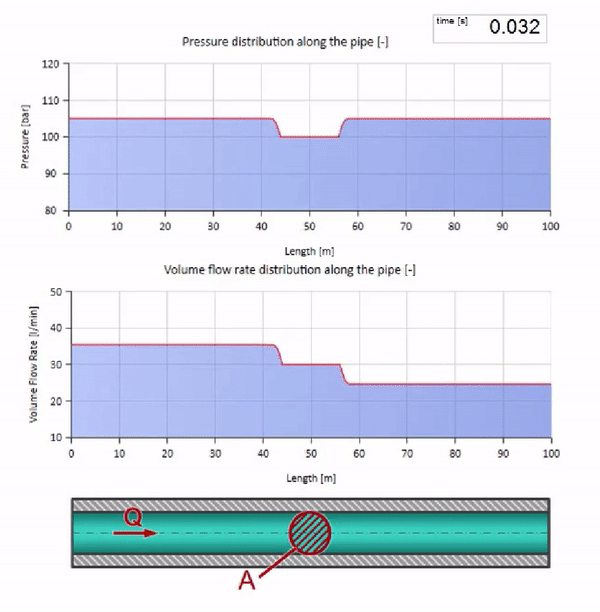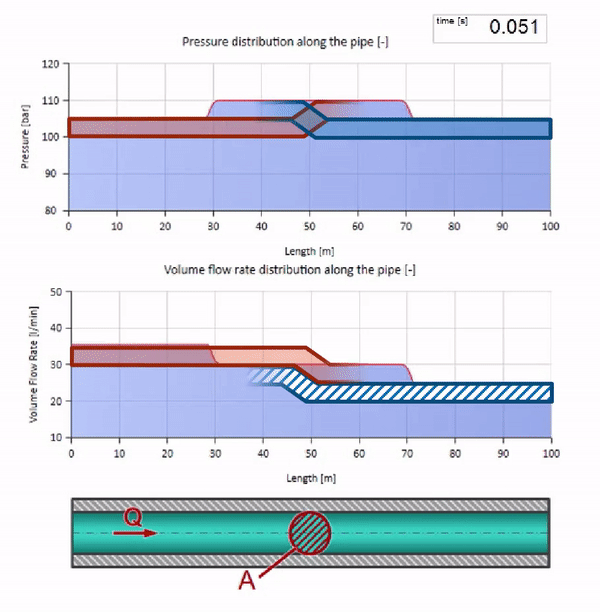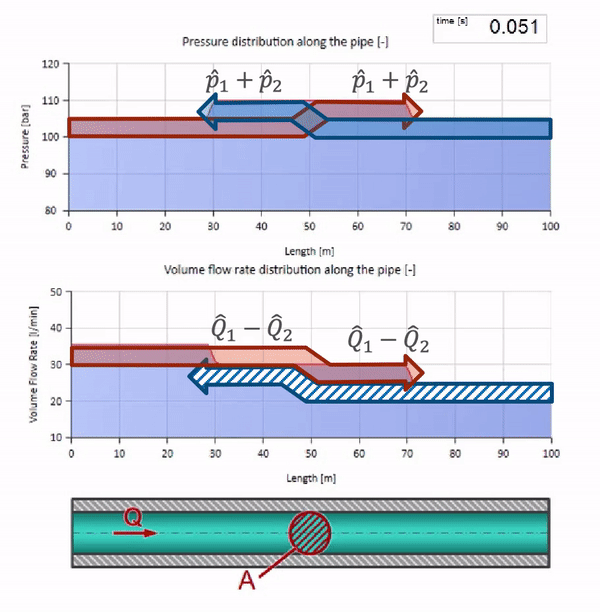

Теперь мы знаем, что у каждой трубы с жидкостью есть такое свойство как волновое сопротивление. Интересно посмотреть что будет с волной, если у трубы на определённом участке резко изменится диаметр: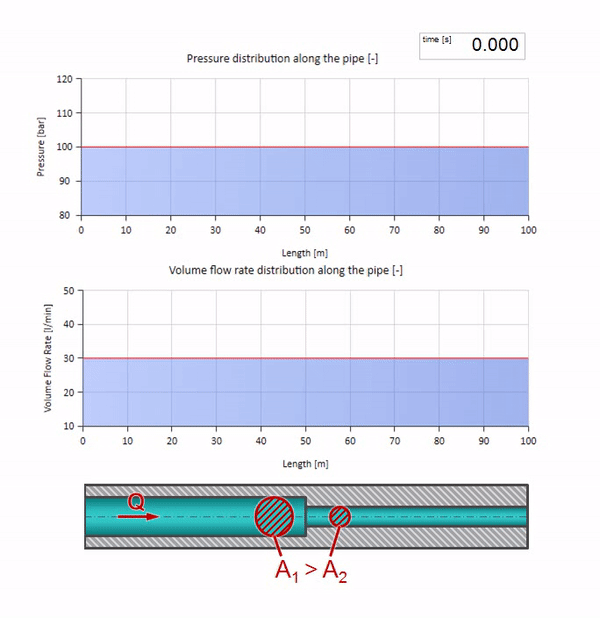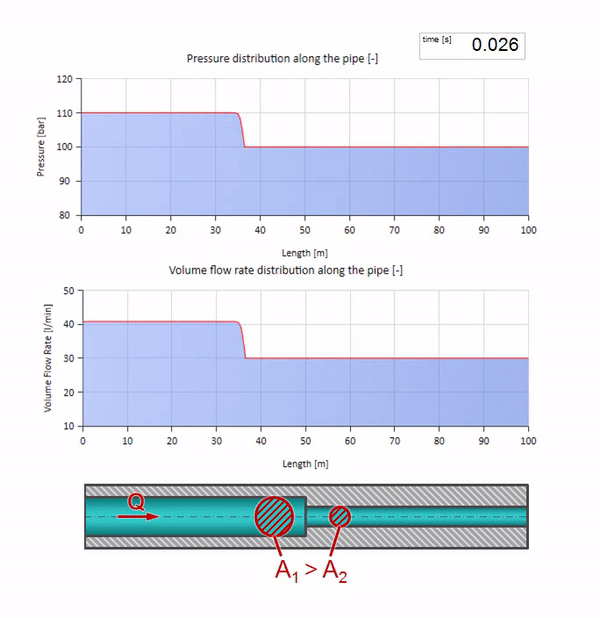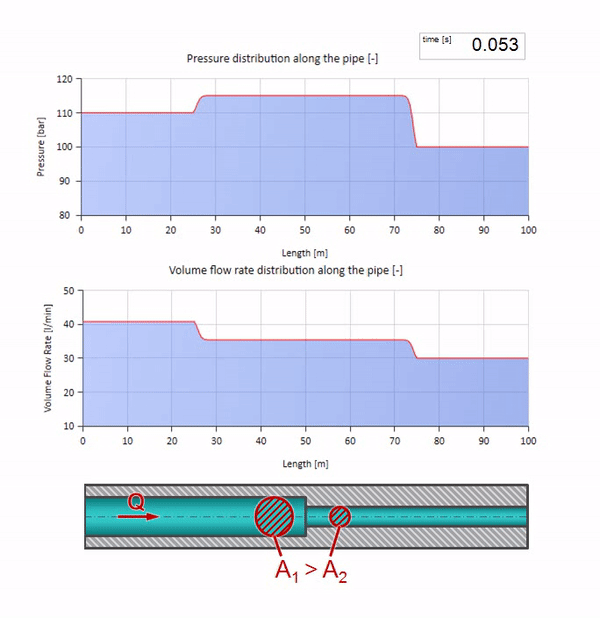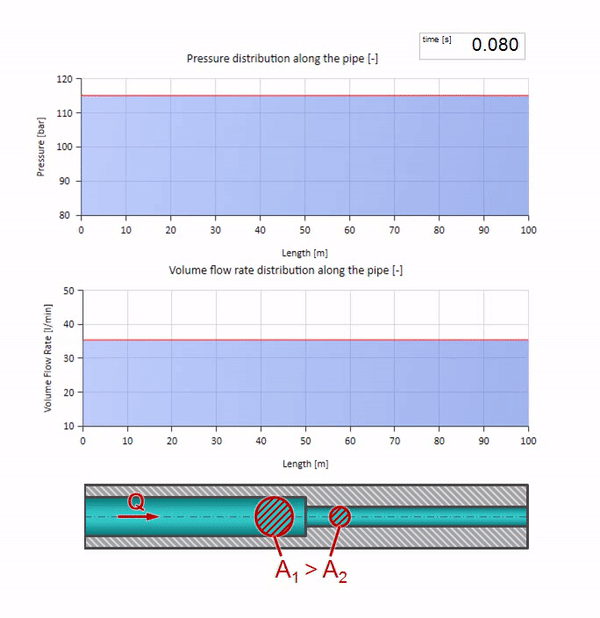

До того как волна дойдёт до места с уменьшением диаметра трубы, разумеется, ничего интересного не происходит. Но далее она достигает участка с бо́льшим волновым сопротивлением, а это значит, что отношение волны давления к волне расхода должно быть больше, чем в левом участке трубы. Это значит, что волна давления должна вырасти, а расхода — уменьшиться. При этом, волне ничего не остаётся, кроме как ещё и отразиться влево, сохраняя равные значения на стыке двух труб.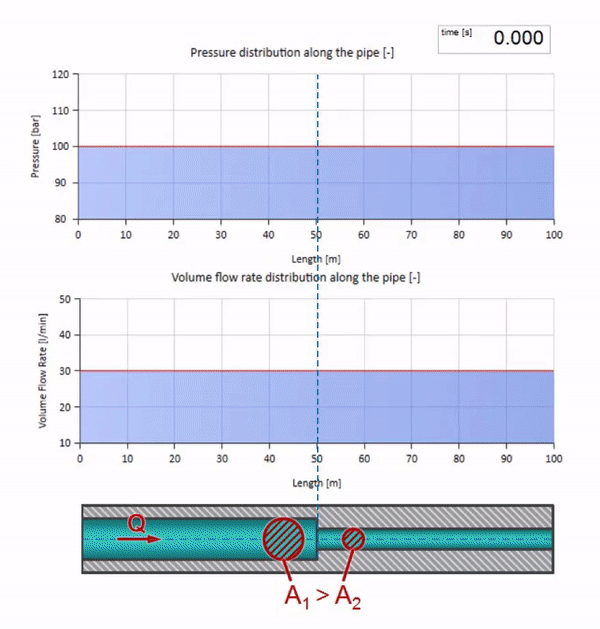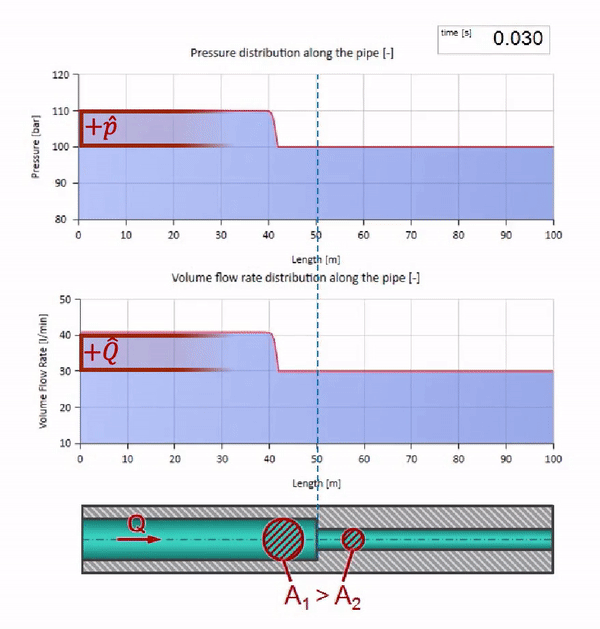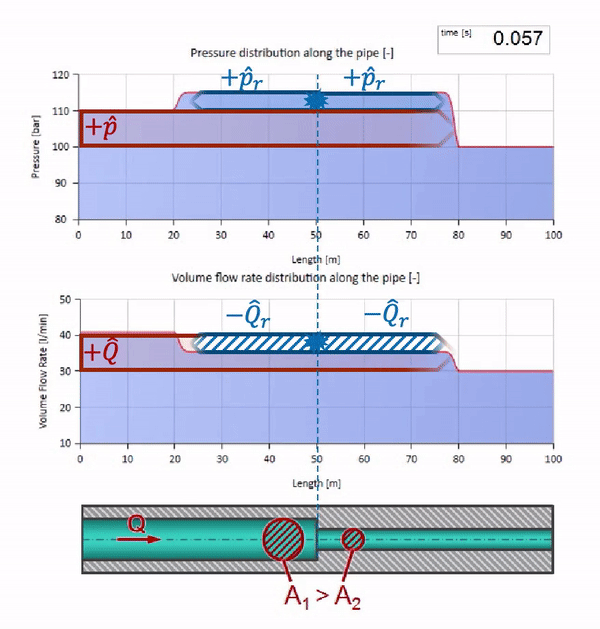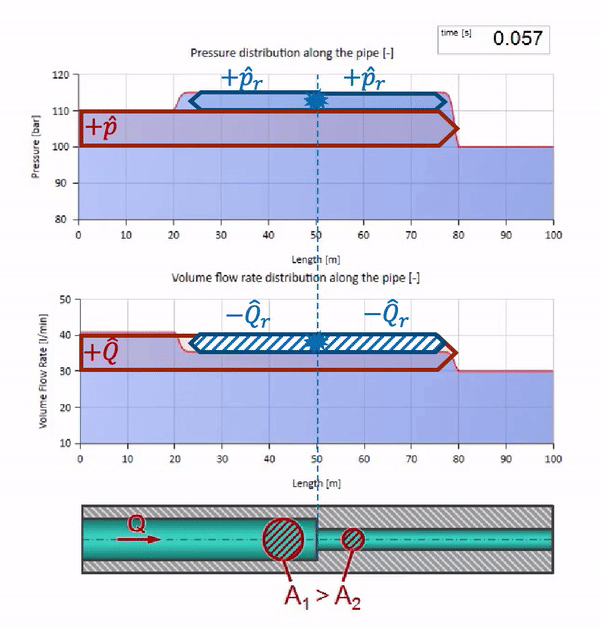

Для расчётов удобно использовать коэффициент отражения $r$ , который считается из волновых сопротивлений отдельных участков:

$r=\frac{Z_2-Z_1}{Z_1+Z_2}$

Тогда отражённые волны давления и расхода можно посчитать так:

${\widehat p}_r=r\;\widehat p$

${\widehat Q}_r=-\frac{\displaystyle\;{\widehat p}_r}{Z_1}=-r\;\widehat Q$

а сами эти волны наложатся по закону интерференции с исходной.
А так будет выглядеть картина отражения волны от участка с меньшим волновым сопротивлением: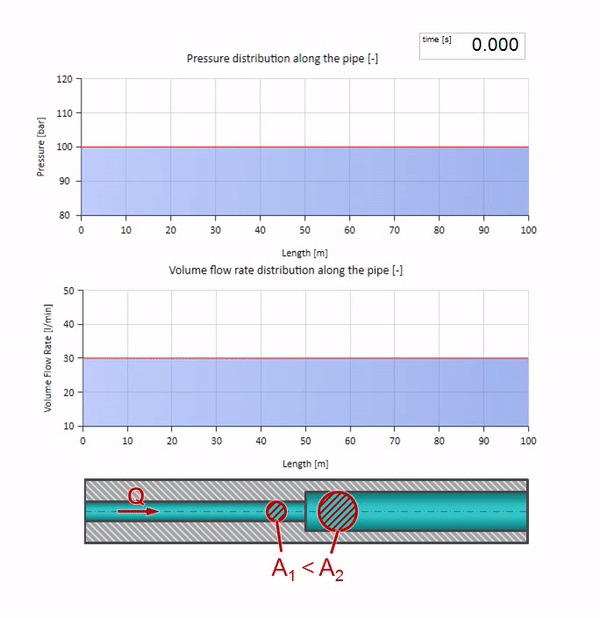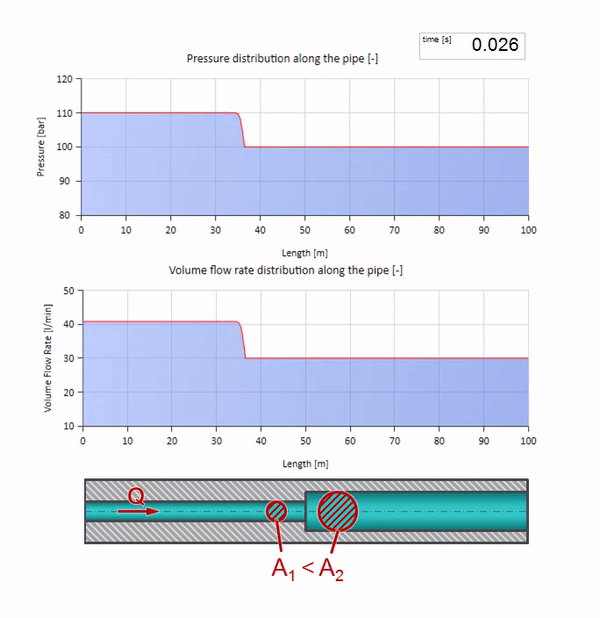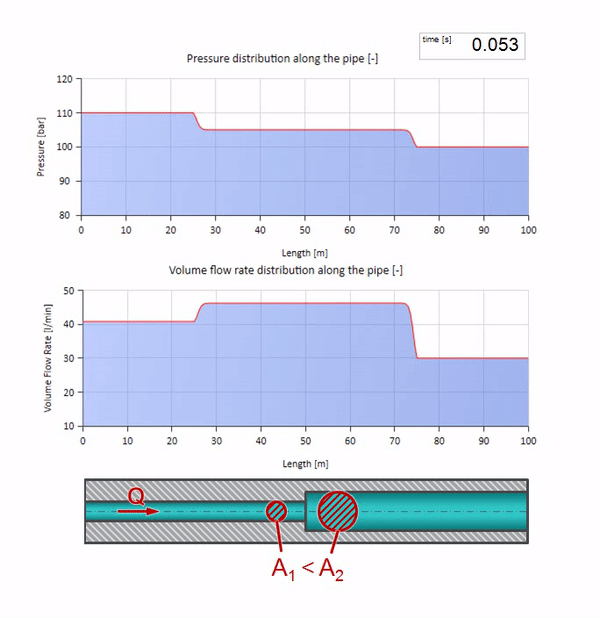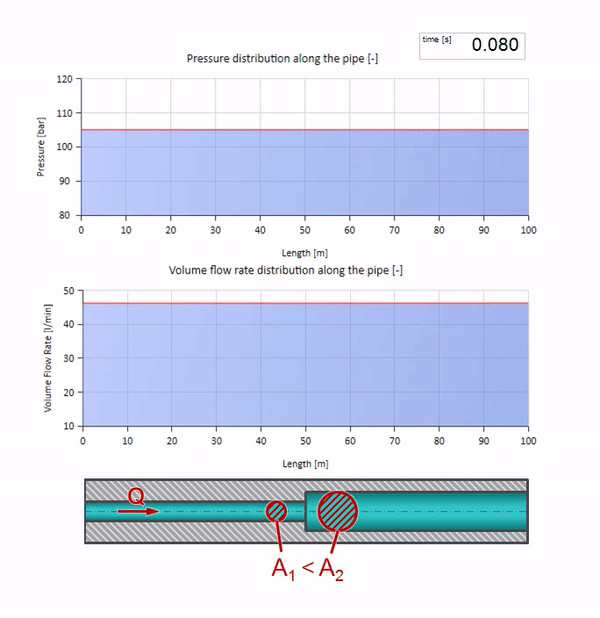

Видно, что на этот раз коэффициент отражения отрицательный, а значит волна давления после отражения будет меньше, а расхода, наоборот — больше.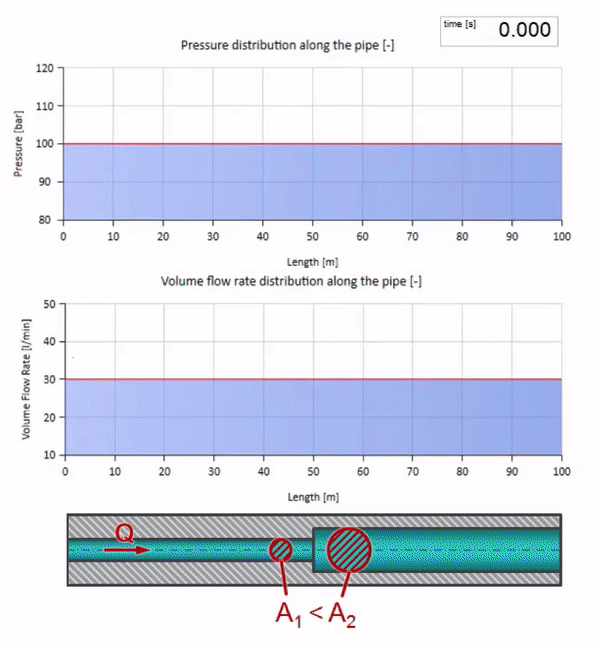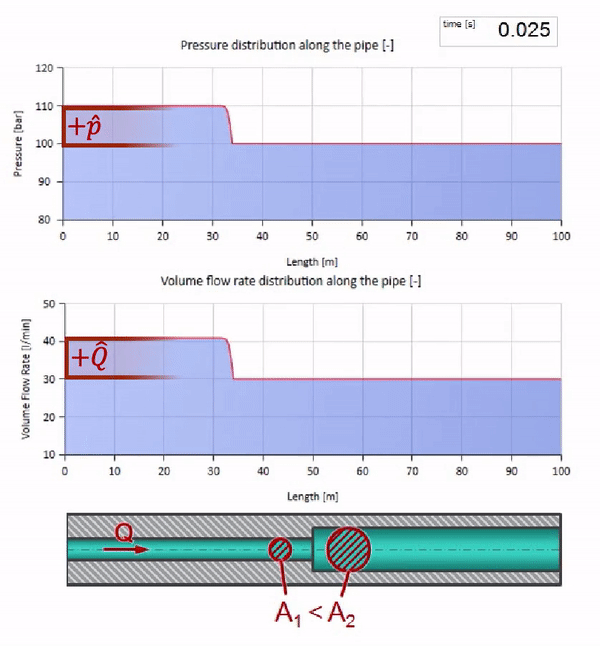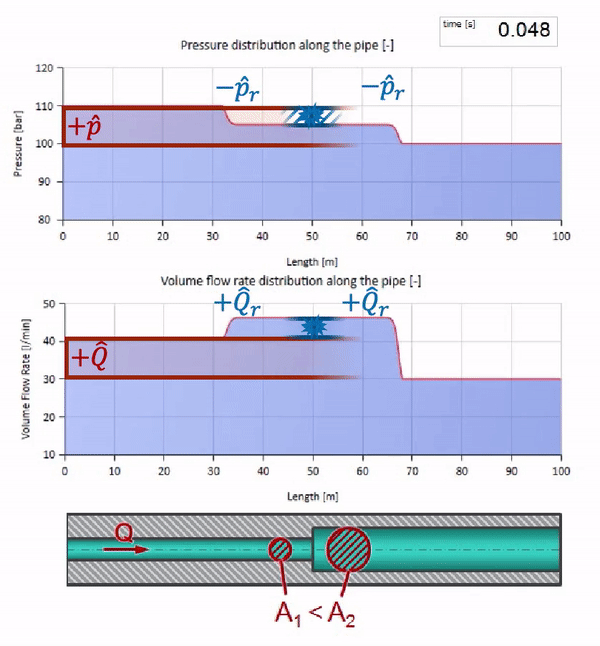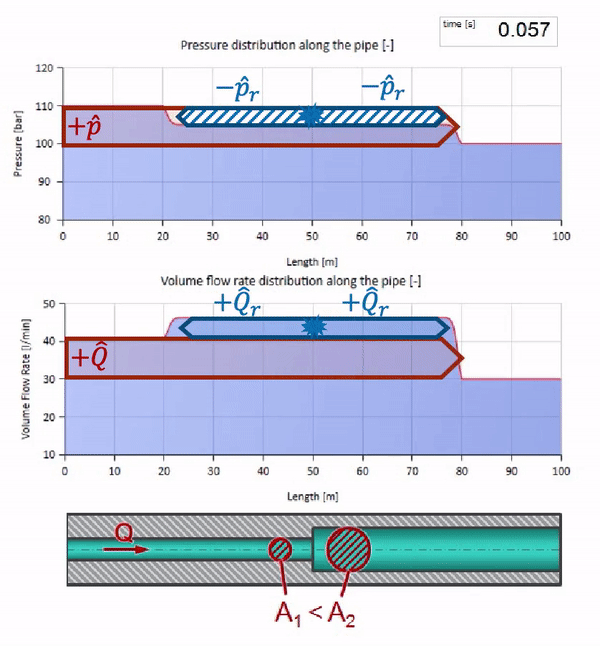

Нужно помнить, что волновое сопротивление зависит не только от размера трубы, но также и от местной скорости звука. Т.е. если у нас есть участок трубы с резиновым рукавом, в котором скорость звука существенно ниже, то волна тоже будет отражаться: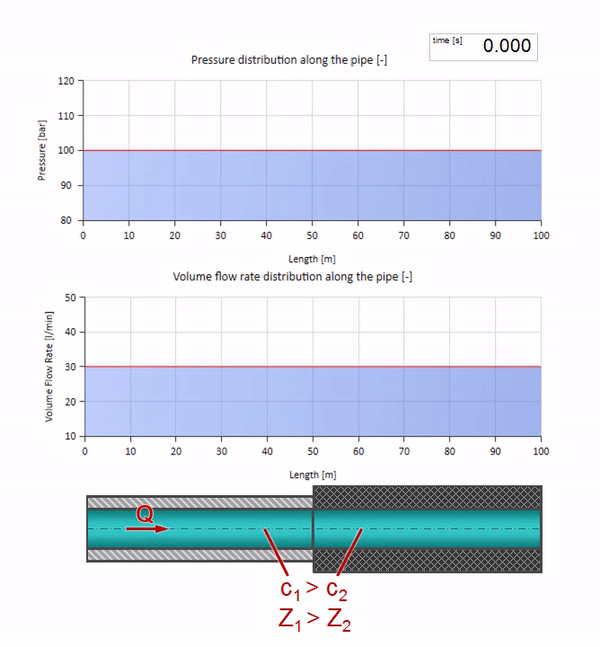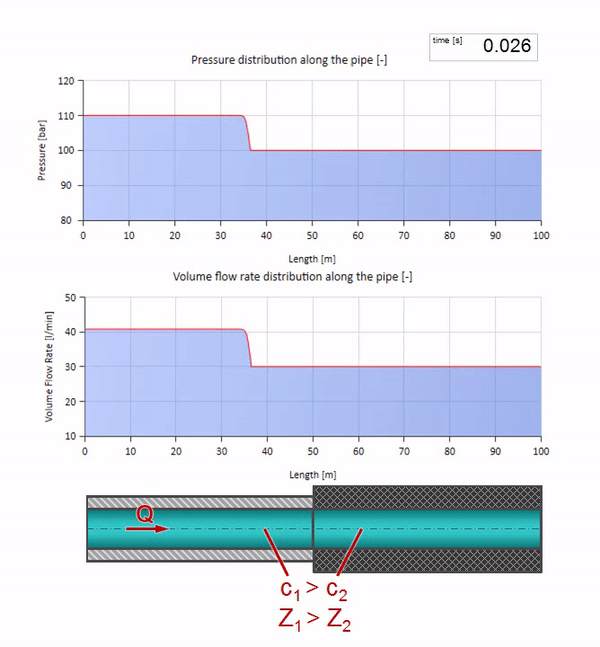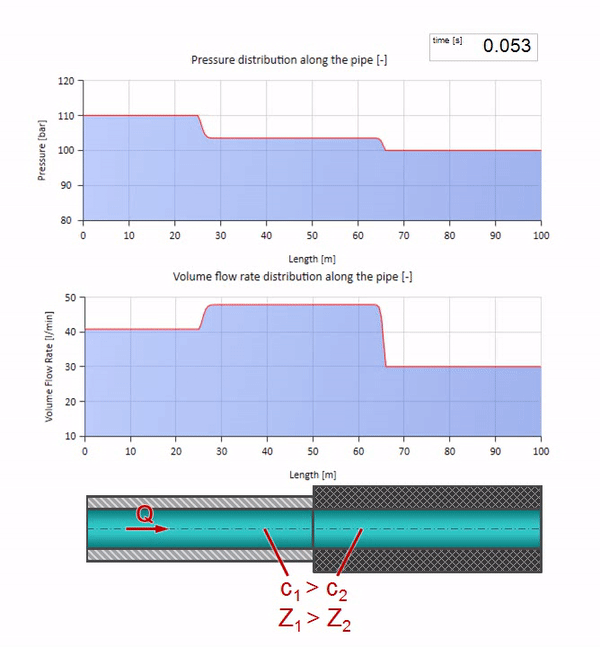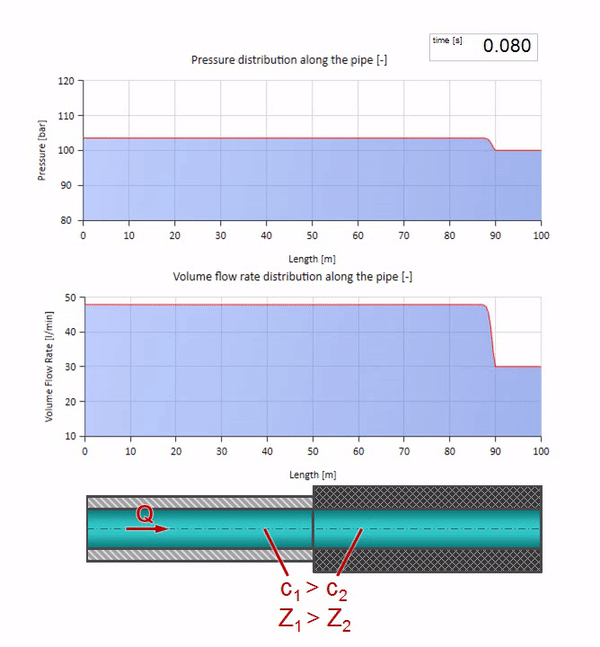

Во-первых, здесь сразу бросается в глаза, что волна в участке с резиновой стенкой трубы движется медленнее. А раз волновое сопротивление у неё ниже, значит результат отражения будет напоминать случай с расширением трубы: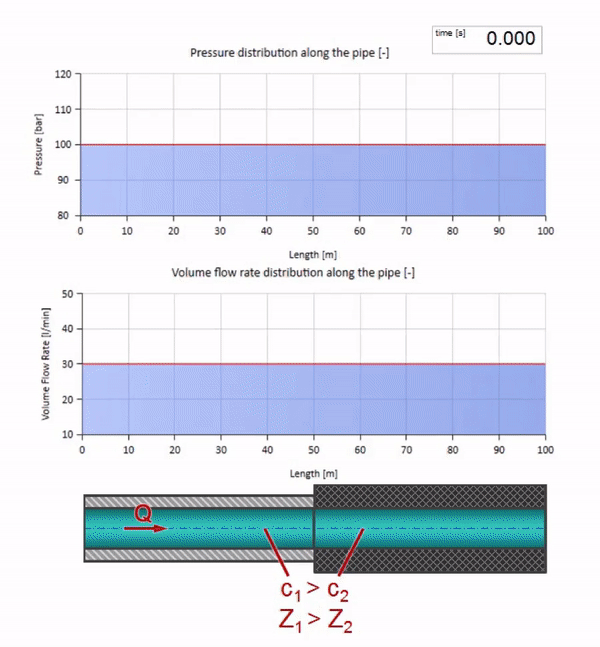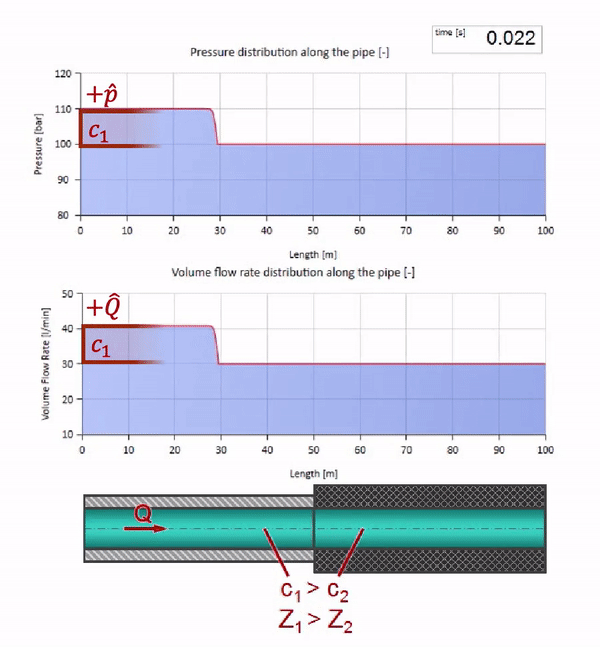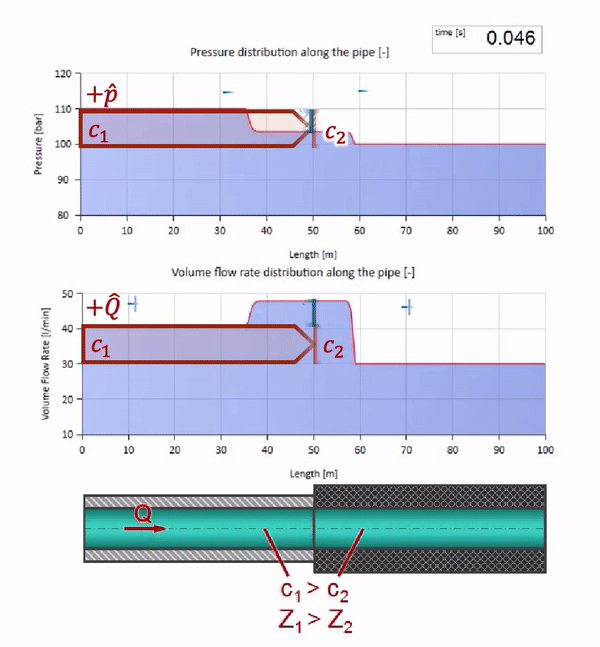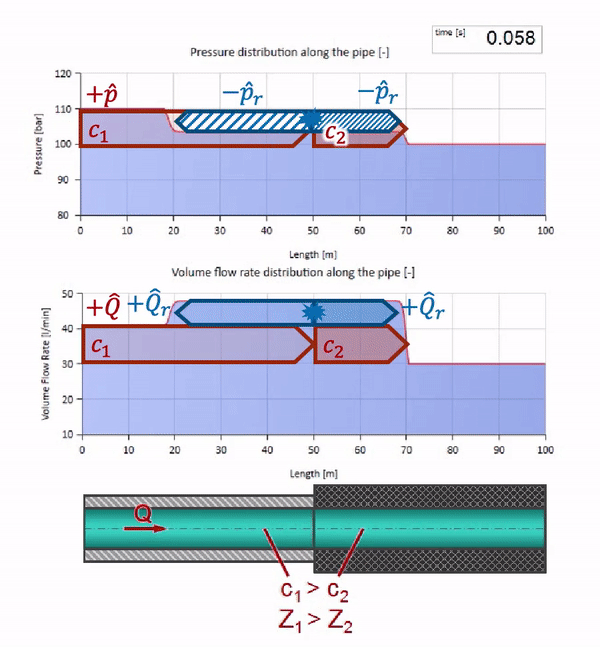

Теперь неплохо бы рассмотреть крайние случаи с нулевым и бесконечно большим значением волнового сопротивления. Это будет выход трубопровода в бак с постоянным давлением и закрытый конец соответственно. Оставлю эти анимации без комментариев: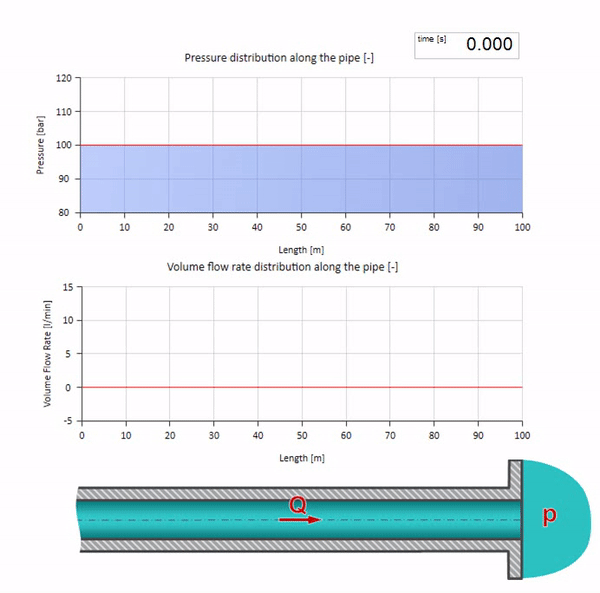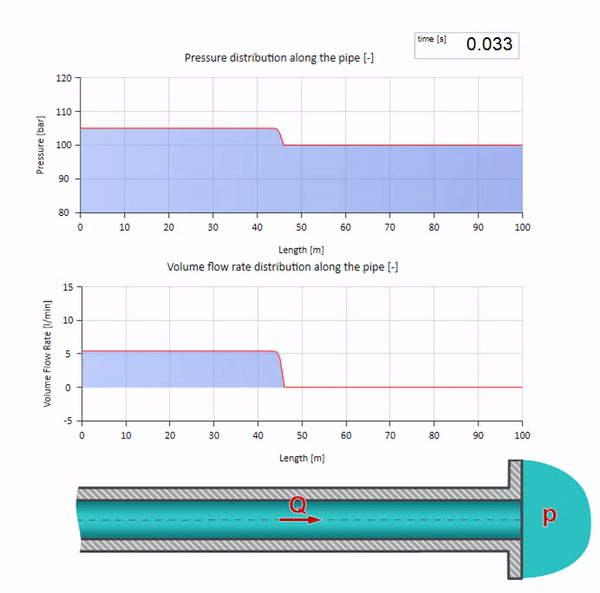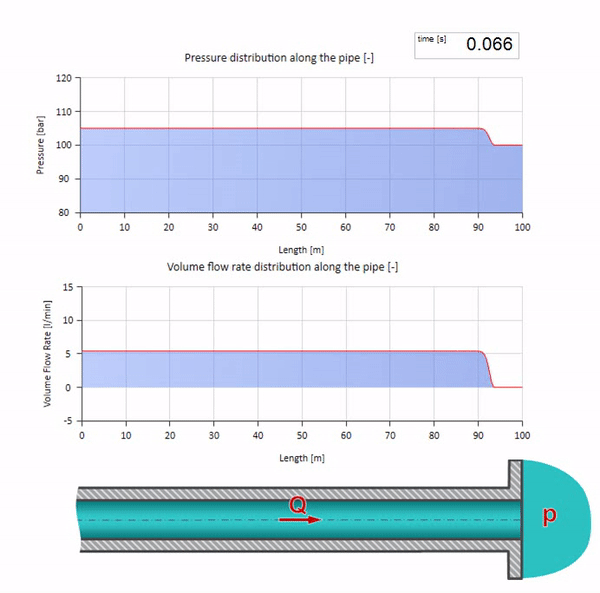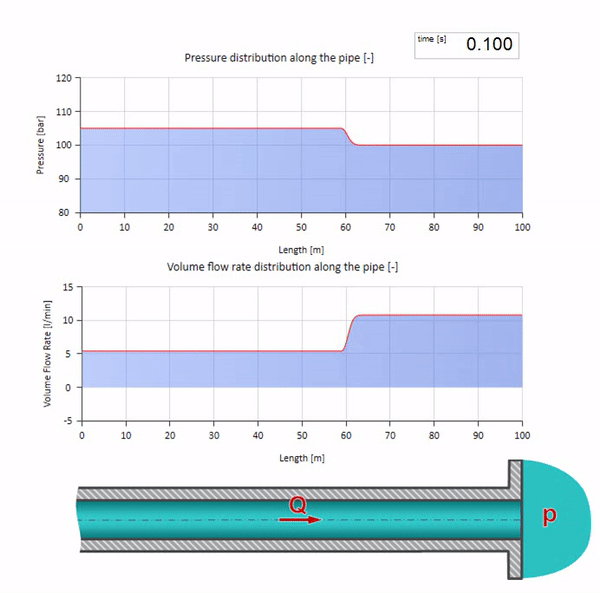

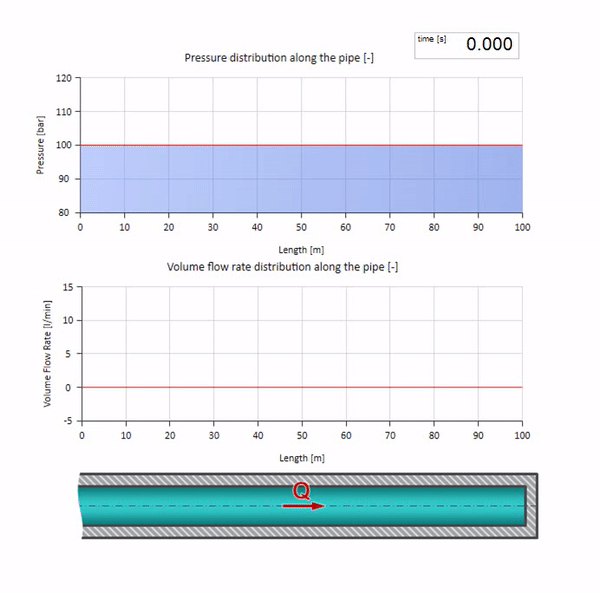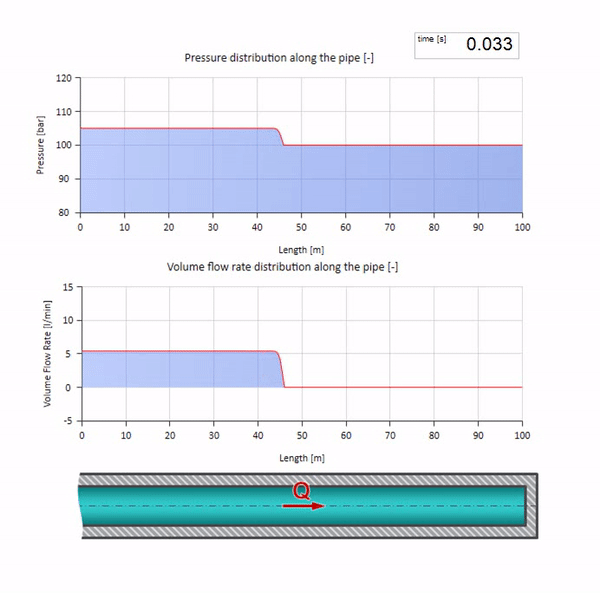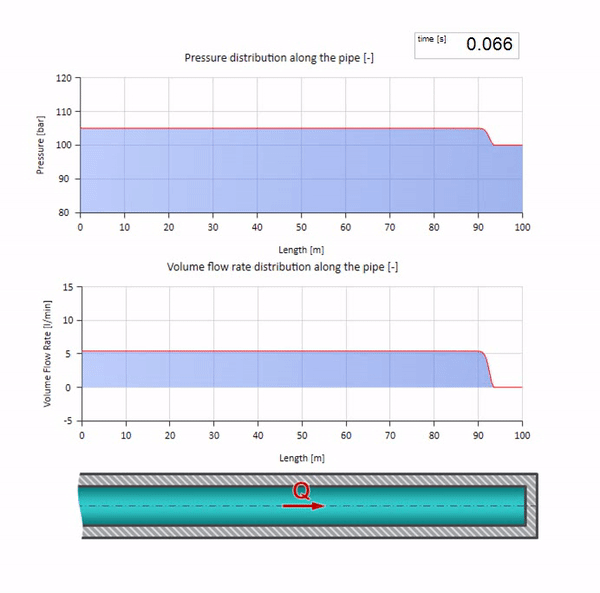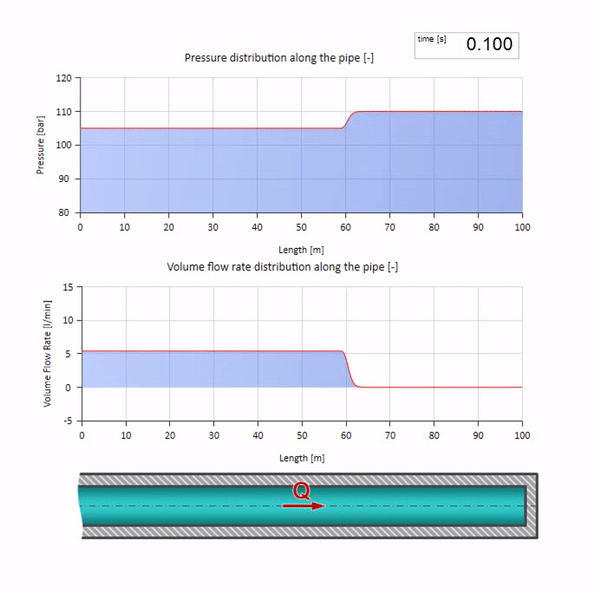
Ну, а если мы объединим два этих случая, то получим классический гидроудар: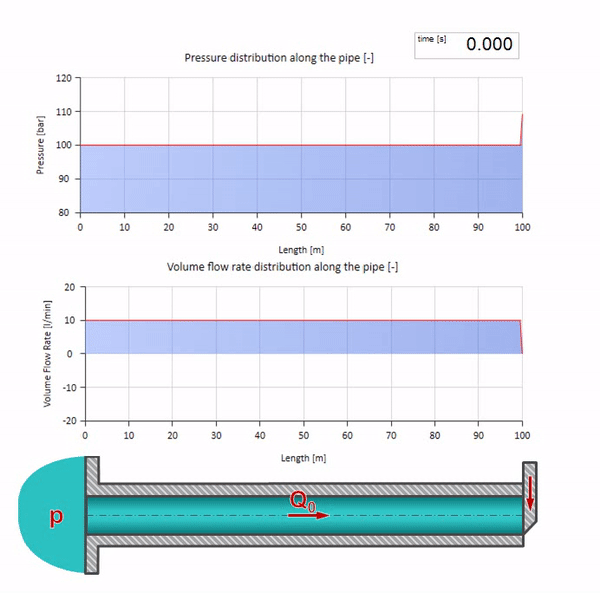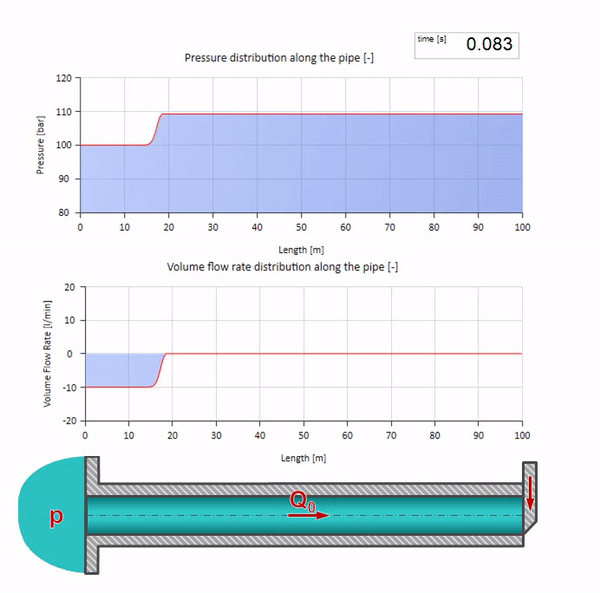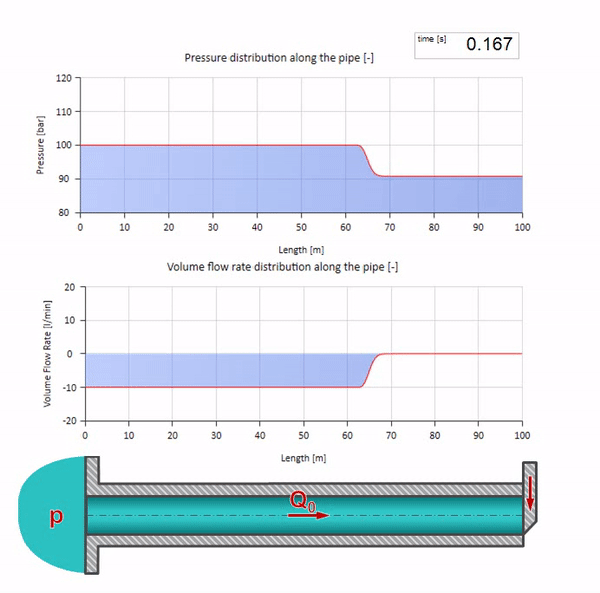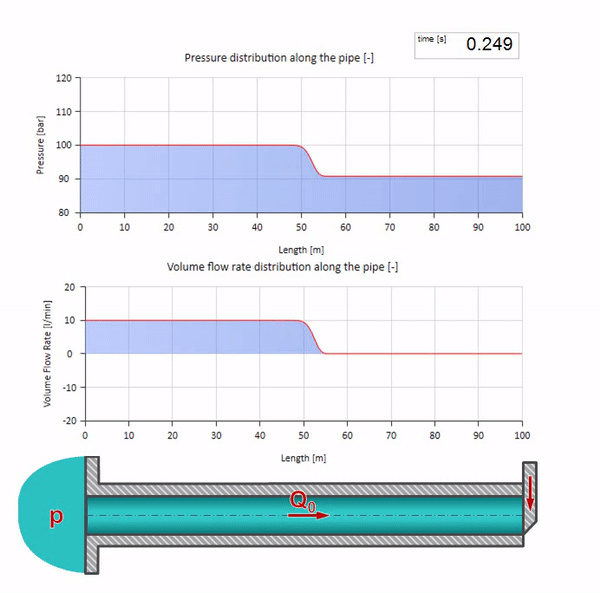

Здесь в начальный момент времени имеется какое-то значение расхода, которое моментально приравнивается нулю на правом конце трубы (закрывается задвижка). Влево начинает двигаться волна падения расхода и роста давления. Эти волны отражаются от правого конца трубопровода с нулевым волновым сопротивлением. При отсутствии трения, процесс этот будет бесконечным.
Что интересно, используя рассмотренные выше формулы, можно вывести уравнение Жуковского для гидроудара:

$\widehat p=Z_L\widehat Q\;$

Выражаем расход через скорость, принимая, что она падает от заданного значения до нуля, и расписываем волновое сопротивление:

$\widehat p=A\;v_0\;\frac{\rho\;c}{\ A}=\rho\;c\;v_0$

Получаем значение возникающего при моментальном закрытии задвижки скачка давления.

Примечания

Написать статью меня вдохновила глава учебника по основам гидравлики кафедры гидравлической техники Рейнско-Вестфальского технического университета Ахена, где, на мой взгляд, понятнее всего описаны процессы в гидравлических линиях (Grundlagen der Fluidtechnik Teil 1: Hydraulik, Hubertus Murrenhoff ISBN: 978–3–8440–1223–1).
Анимации сделаны в программе SimulationX, расчёт проводился методом характеристик