Визуализация странных аттракторов в Plotly — это шедеврально17.12.2019 05:18

Поэзия — это очень красивый, зачастую глубокомысленный слог, которым мы не пользуемся в обыденной жизни, но так им любим наслаждаться. То же самое можно сказать и о математике. В фильме «Пи» главный герой называет математику «языком природы», а в фильме «Игры разума» главный герой говорит о ней, как об «особом виде искусства». Мы же, в обыденной жизни, можем напрочь забыть об этом.

Облик странных аттракторов необычен и притягателен даже в двумерном измерении. Plotly позволяет строить их в трех измерениях, причем он дает возможность очень легко получить именно 3D-модель, которую можно «вертеть» и сквозь которую можно «пролетать» — ощущение «прикосновения».

С чего все началось

Все началось очень давно, где-то в 2007 году в университете я познакомился с теорией самоорганизации и впервые увидел аттрактор Лоренца, его черно-белую иллюстрацию в какой-то книге. Тогда мне показалось слишком странным, что нечто может двигаться по столь необычной траектории. Еще более странным мне казалась сама идея того, что практически все на свете может быть описано одной-единственной теорией.

В общем, все как обычно — мое мировоззрение поменялось, жизнь продолжалась, время шло. И вот, совсем недавно я натыкаюсь на ссылку и вижу вот это:

Изображение взято с сайта chaoticatmospheres.com

«Красиво.» — подумал я. Мысль о том, что все это можно построить в Matplotlib тоже промелькнула, но я уже заранее знал, что ничего впечатляющего не получится. И вот совсем недавно, буквально две недели назад, я познакомился с Plotly и сразу понял, что из этого может что-то получиться.

Первая попытка построения сразу же провалилась. Оказалось, что формулы на некоторых изображениях «Галереи странных аттракторов» содержат ошибки. Впрочем, автор галереи, честно предупреждает о том, что не является математиком, как и автор этой статьи.

Недолгое «гугление» позволило найти вот этот код, который оказался чрезвычайно полезен, а создал его Michael Tyka. Этот замечательный человек сделал целый плагин для Blender-а, позволяющий строить модели (!) 60-ти аттракторов. Фактически, их можно распечатать на 3D-принтере, а учитывая, что есть технологии печати воском, то можно довольно легко получить форму для отливки в бронзе.

Код для визуализации

Что ж, помимо, того что я являюсь математиком-любителем, я так же являюсь любителем-программистом. Так что не судите строго за качество кода.

################################
###  ИМПОРТИРУЕМ БИБЛИОТЕКИ  ###
################################

import numpy as np
from scipy.integrate import odeint
import plotly.graph_objects as go


##################################
###  РЕШАЕМ СИСТЕМУ УРАВНЕНИЙ  ###
##################################

# Система уравнений:
def LorenzMod1(XYZ, t, alpha, beta, xi, delta):
    x, y, z = XYZ
    x_dt = -alpha*x + y*y - z*z + alpha*xi
    y_dt = x*(y - beta*z) + delta
    z_dt = -z + x*(beta*y + z)
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 0.1
beta = 4
xi = 14
delta = 0.08

x_0, y_0, z_0 = 0, 1, 0

# Максимальное время и общее количество
# временных точек:
tmax, n = 100, 50000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(LorenzMod1, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta))
X, Y, Z = f.T


#######################
###  ВИЗУАЛИЗИРУЕМ  ###
#######################

# Массив, отвечающий за изменение цвета:
c = np.linspace(0, 1, n)

# Готовим данные для отрисовки:
DATA = go.Scatter3d(x=X, y=Y, z=Z,
                    line=dict(color= c,
                              width=3,
                              # Выбираем цветовую палитру:
                              # Greys,YlGnBu,Greens,YlOrRd,Bluered,RdBu,
                              # Reds,Blues,Picnic,Rainbow,Portland,Jet,
                              # Hot,Blackbody,Earth,Electric,Viridis,Cividis.
                              colorscale="Cividis"),
                    #  Рисуем только линии:
                    mode='lines')

fig = go.Figure(data=DATA)    

# Задаем параметры отрисовки:
fig.update_layout(width=1000, height=1000,
                  margin=dict(r=10, l=10, b=10, t=10),
                  # Устанавливаем цвет фона:
                  paper_bgcolor='rgb(0,0,0)',
                  scene=dict(camera=dict(up=dict(x=0, y=0, z=1),
                                         eye=dict(x=0, y=1, z=1)),
                             # Устанавливаем пропорциональное
                             # соотношение осей друг к другу:
                             aspectratio = dict(x=1, y=1, z=1),
                             # Отображаем, как указано в "aspectratio"
                             aspectmode = 'manual',
                             # Скрываем оси:
                             xaxis=dict(visible=False),
                             yaxis=dict(visible=False),
                             zaxis=dict(visible=False)
                            )
                 )

######################
#!!  ВОСТОРГАЕМСЯ  !!#
######################

fig.show()

В результате должна появиться 3D-модель странного аттрактора, называемого Lorenz Mod 1:

Нужно сразу отметить, что для решения систем дифференциальных уравнений была выбрана функция odeint из модуля SciPy, которая показалась мне самым простым и быстрым выходом для создания работающего кода. Однако, все уравнения могут решаться обычным методом Эйлера.

Для обозначения коэффициентов в коде я по привычке использовал названия греческих букв принятых в LaTeX-е. В работе с блокнотами Jupyter это иногда бывает очень полезно, так-как формулы могут быстро стать кодом, а код может быстро превратиться в формулы.

Если вы новичок в экосистеме Python, но хотите, что бы код гарантированно выполнился, то лучше всего установите последнюю версию дистрибутива Python Anaconda, а пакет Plotly через conda — встроенный менеджер пакетов дистрибутива.

Учитывая огромное количество странных аттракторов, построить их все, мне не представляется возможным. Поэтому, в этой статье я приведу лишь самые интересные из тех, что мне удалось построить.

The Chen-Lee Attractor

# Система уравнений:
def ChenLee(XYZ, t, alpha, beta, delta):
    x, y, z = XYZ
    x_dt = alpha*x - y*z
    y_dt = beta*y + x*z
    z_dt = delta*z + x*y/3
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 5
beta = -10
delta = -0.38

x_0, y_0, z_0 = 1, 1, 1

# Максимальное время и общее количество
# временных точек:
tmax, n = 200, 30000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(ChenLee, (x_0, y_0, z_0), t,
           args=(alpha, beta, delta))

The Chua Attractor

# Система уравнений:
def ChuaAttractor(XYZ, t, alpha, beta, zeta, delta):
    x, y, z = XYZ
    h = zeta*x + (0.5*(delta - zeta))*(np.abs(x + 1) - np.abs(x - 1))
    x_dt = alpha*(-x + y - h)
    y_dt = x - y + z
    z_dt = -beta*y
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 15.6
beta = 25.58
zeta = -5/7
delta = -8/7

x_0, y_0, z_0 = 1.8, -0.7, -2.85

# Максимальное время и общее количество
# временных точек:
tmax, n = 200, 10000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(ChuaAttractor, (x_0, y_0, z_0), t,
           args=(alpha, beta, zeta, delta))

The Coullet Attractor

# Система уравнений:
def Coullet(XYZ, t, alpha, beta, zeta, delta):
    x, y, z = XYZ
    x_dt = y
    y_dt = z
    z_dt = alpha*x + beta*y + zeta*z + delta*x**3
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 0.8
beta = -1.1
zeta = -0.4
delta = -1

x_0, y_0, z_0 = 0.1, 0, 0

# Максимальное время и общее количество
# временных точек:
tmax, n = 200, 20000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(Coullet, (x_0, y_0, z_0), t,
           args=(alpha, beta, zeta, delta))

The Dadras Attractor

# Система уравнений:
def DadrasAttractor(XYZ, t, rho, sigma, tau, zeta, epsilon):
    x, y, z = XYZ
    x_dt = y - rho*x + sigma*y*z
    y_dt = tau*y - x*z + z
    z_dt = zeta*x*y - epsilon*z
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
rho = 3
sigma = 2.7
tau = 1.7
zeta = 2
epsilon = 9

x_0, y_0, z_0 = 0.1, 0.03, 0

# Максимальное время и общее количество
# временных точек:
tmax, n = 220, 40000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(DadrasAttractor, (x_0, y_0, z_0), t,
           args=(rho, sigma, tau, zeta, epsilon))

The Dequan Li Attractor

# Система уравнений:
def DequanLi(XYZ, t, alpha, beta, delta, epsilon, rho, xi):
    x, y, z = XYZ
    x_dt = alpha*(y - x) + delta*x*z
    y_dt = rho*x + xi*y -x*z
    z_dt = beta*z + x*y  - epsilon*x*x
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 40
beta = 1.833
delta = 0.16
epsilon = 0.65
rho = 55
xi = 20

x_0, y_0, z_0 = 0.01, 0, 0

# Максимальное время и общее количество
# временных точек:
tmax, n = 50, 40000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(DequanLi, (x_0, y_0, z_0), t,
           args=(alpha, beta, delta, epsilon, rho, xi))

The Finance Attractor

# Система уравнений:
def FinanceAttractor(XYZ, t, alpha, beta, zeta):
    x, y, z = XYZ
    x_dt = (1/beta - alpha)*x + x*y + z
    y_dt = -beta*y - x**2
    z_dt = -x - zeta*z
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 0.001
beta = 0.2
zeta = 1.1

x_0, y_0, z_0 = 0.1, 0, 0

# Максимальное время и общее количество
# временных точек:
tmax, n = 300, 40000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(FinanceAttractor, (x_0, y_0, z_0), t,
           args=(alpha, beta, zeta))

The Four-Wing Attractor

# Система уравнений:
def FourWing(XYZ, t, alpha, beta, zeta):
    x, y, z = XYZ
    x_dt = alpha*x + y + y*z
    y_dt = -x*z + y*z
    z_dt = -z - zeta*x*y + beta
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 5
beta = 16
zeta = 2

x_0, y_0, z_0 = 1, -1, 1

# Максимальное время и общее количество
# временных точек:
tmax, n = 100, 60000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(FourWing, (x_0, y_0, z_0), t,
           args=(alpha, beta, zeta))

The Hadley Attractor

# Система уравнений:
def HadleyAttractor(XYZ, t, alpha, beta, xi, delta):
    x, y, z = XYZ
    x_dt = -y*y - z*z - alpha*x + alpha*xi
    y_dt = x*y - beta*x*z - y + delta
    z_dt = beta*x*y + x*z-z
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 0.2
beta = 4
xi = 8
delta = 1

x_0, y_0, z_0 = 0.39, -1, 0

# Максимальное время и общее количество
# временных точек:
tmax, n = 100, 10000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(HadleyAttractor, (x_0, y_0, z_0), t,
           args=(alpha, beta, xi, delta))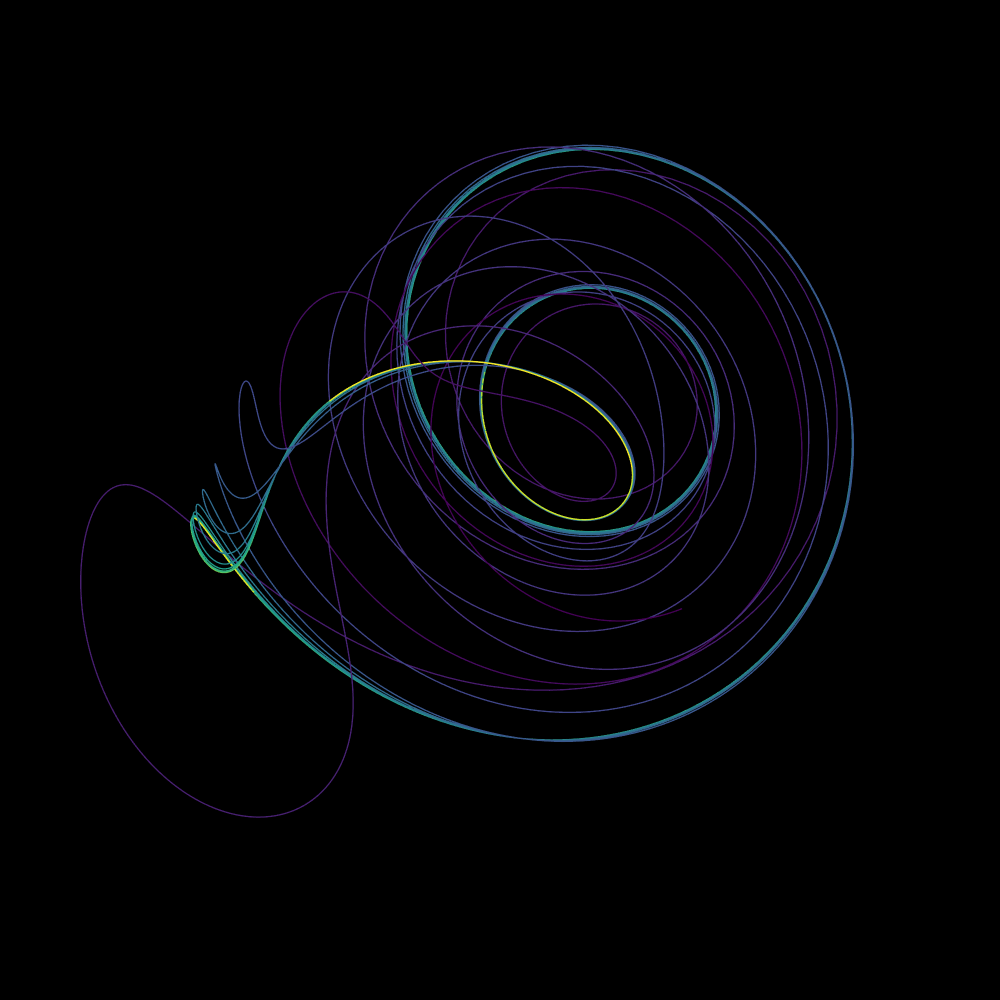

The Halvorsen Attractor

# Система уравнений:
def HalvorsenAttractor(XYZ, t, alpha):
    x, y, z = XYZ
    x_dt = -alpha*x - 4*y - 4*z - y*y
    y_dt = -alpha*y - 4*z - 4*x - z*z
    z_dt = -alpha*z - 4*x - 4*y - x*x
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 1.4

x_0, y_0, z_0 = -5, 0, 0

# Максимальное время и общее количество
# временных точек:
tmax, n = 100, 10000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(HalvorsenAttractor, (x_0, y_0, z_0), t,
           args=(alpha,))

The Liu-Chen Attractor

# Система уравнений:
def LiuChen(XYZ, t, alpha, beta, sigma, delta, epsilon, xi):
    x, y, z = XYZ
    x_dt = alpha*y + beta*x + sigma*y*z
    y_dt = delta*y - z + epsilon*x*z
    z_dt = xi*z - x*y
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 2.4
beta = -3.75
sigma = 14
delta = -11
epsilon = 4
xi = 5.58

x_0, y_0, z_0 = 1, 3, 5

# Максимальное время и общее количество
# временных точек:
tmax, n = 55, 50000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(LiuChen, (x_0, y_0, z_0), t,
           args=(alpha, beta, sigma, delta, epsilon, xi))

The Lorenz Mod 2 Attractor

# Система уравнений:
def LorenzMod2(XYZ, t, alpha, beta, xi, delta):
    x, y, z = XYZ
    x_dt = -alpha*x + y**2 -z**2 + alpha*xi
    y_dt = x*(y - beta*z) + delta
    z_dt = -z + x*(beta*y + z)
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 0.9
beta = 5
xi = 9.9
delta = 1

x_0, y_0, z_0 = 5, 5, 5

# Максимальное время и общее количество
# временных точек:
tmax, n = 50, 50000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(LorenzMod2, (x_0, y_0, z_0), t,
           args=(alpha, beta, xi, delta))

The Modified Chua Chaotic Attractor

# Система уравнений:
def ChuaModified(XYZ, t, alpha, beta, gamma, delta, zeta):
    x, y, z = XYZ
    h = -delta*np.sin((np.pi*x)/(2*gamma))
    x_dt = alpha*(y - h)
    y_dt = x - y + z
    z_dt = -beta*y
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 10.82
beta = 14.286
gamma = 1.3
delta = 0.11
zeta = 7

x_0, y_0, z_0 = 1, 1, 0

# Максимальное время и общее количество
# временных точек:
tmax, n = 200, 10000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(ChuaModified, (x_0, y_0, z_0), t,
           args=(alpha, beta, gamma, delta, zeta))

The Newton Leipnik Attractor

# Система уравнений:
def NewtonLeipnik(XYZ, t, alpha, beta):
    x, y, z = XYZ
    x_dt = -alpha*x + y + 10*y*z
    y_dt = -x - 0.4*y + 5*x*z
    z_dt = beta*z - 5*x*y
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 0.4
beta = 0.175

x_0, y_0, z_0 = 0.349, 0, -0.16

# Максимальное время и общее количество
# временных точек:
tmax, n = 300, 50000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(NewtonLeipnik, (x_0, y_0, z_0), t,
           args=(alpha, beta))

The Nose-Hoover Attractor

# Система уравнений:
def NoseHoover(XYZ, t, alpha):
    x, y, z = XYZ
    x_dt = y
    y_dt = -x + y*z
    z_dt = alpha - y*y
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 1.5

x_0, y_0, z_0 = 1, 0, 0

# Максимальное время и общее количество
# временных точек:
tmax, n = 150, 10000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(NoseHoover, (x_0, y_0, z_0), t,
           args=(alpha,))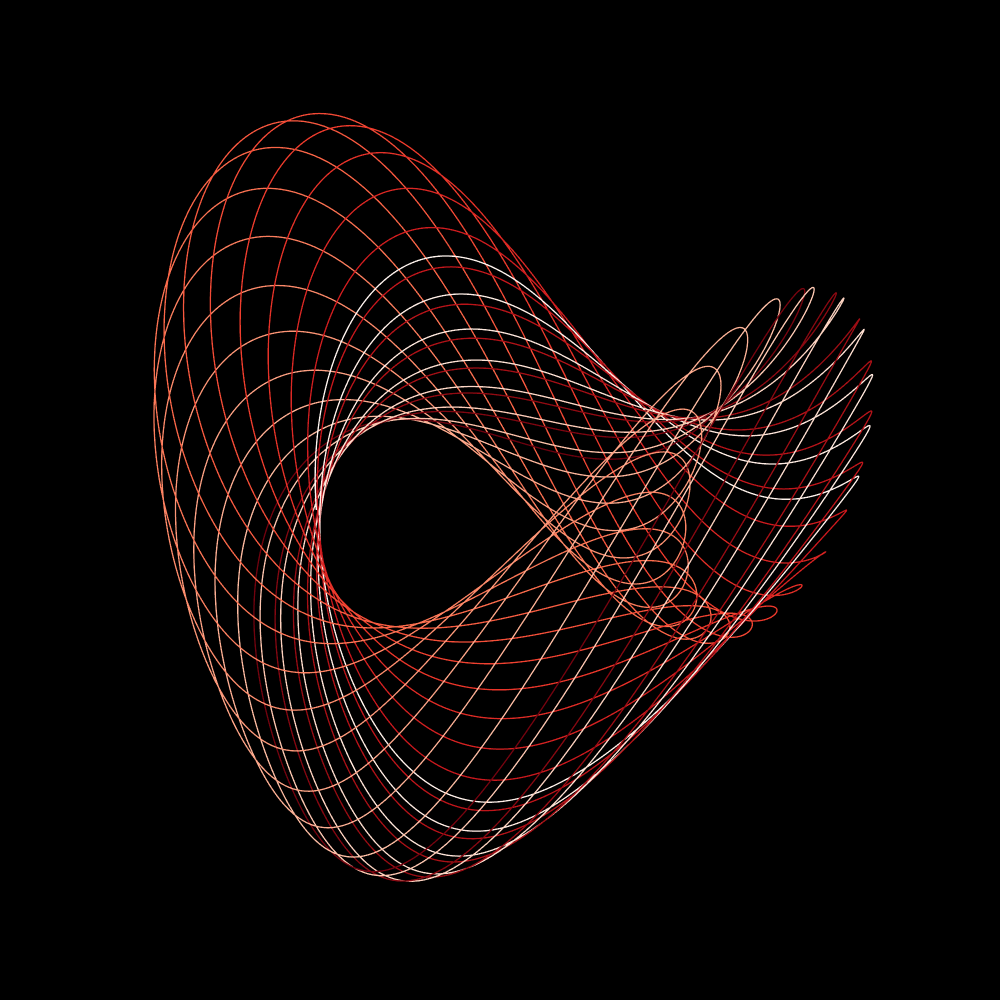

The Roessler Attractor

# Система уравнений:
def Roessler(XYZ, t, alpha, beta, sigma):
    x, y, z = XYZ
    x_dt = -(y + z)
    y_dt = x + alpha*y
    z_dt = beta + z*(x - sigma)
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 0.2
beta = 0.2
sigma = 5.7

x_0, y_0, z_0 = 1, 1, 1

# Максимальное время и общее количество
# временных точек:
tmax, n = 300, 50000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(Roessler, (x_0, y_0, z_0), t,
           args=(alpha, beta, sigma))

The Sakarya Attractor

# Система уравнений:
def SakaryaAttractor(XYZ, t, alpha, beta):
    x, y, z = XYZ
    x_dt = -x + y + y*z
    y_dt = -x - y + alpha*x*z
    z_dt = z - beta*x*y
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 0.4
beta = 0.3

x_0, y_0, z_0 = 1, -1, 1

# Максимальное время и общее количество
# временных точек:
tmax, n = 100, 10000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(SakaryaAttractor, (x_0, y_0, z_0), t,
           args=(alpha, beta))

The Thomas Attractor

# Система уравнений:
def Thomas(XYZ, t, beta):
    x, y, z = XYZ
    x_dt = -beta*x + np.sin(y)
    y_dt = -beta*y + np.sin(z)
    z_dt = -beta*z + np.sin(x)
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
beta = 0.19

x_0, y_0, z_0 = 0.1, 0, 0

# Максимальное время и общее количество
# временных точек:
tmax, n = 185, 10000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(Thomas, (x_0, y_0, z_0), t,
           args=(beta,))

The Three-Scroll Unified Chaotic System Attractor (TSUCS1)

# Система уравнений:
def TSUCS1(XYZ, t, alpha, beta, delta, epsilon, xi):
    x, y, z = XYZ
    x_dt = alpha*(y - x) + delta*x*z
    y_dt = xi*y - x*z
    z_dt = beta*z + x*y  - epsilon*x*x
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 40
beta = 0.833
delta = 0.5
epsilon = 0.65
xi = 20

x_0, y_0, z_0 = 0.01, 0, 0

# Максимальное время и общее количество
# временных точек:
tmax, n = 70, 50000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(TSUCS1, (x_0, y_0, z_0), t,
           args=(alpha, beta, delta, epsilon, xi))

The Wang-Sun Attractor

# Система уравнений:
def WangSunAttractor(XYZ, t, alpha, beta, zeta, delta, epsilon, xi):
    x, y, z = XYZ
    x_dt = alpha*x + zeta*y*z
    y_dt = beta*x + delta*y - x*z
    z_dt = epsilon*z + xi*x*y
    return x_dt, y_dt, z_dt

# Параметры системы и начальные условия:
alpha = 0.2
beta = -0.01
zeta = 1
delta = -0.4
epsilon = -1
xi = -1

x_0, y_0, z_0 = 0.5, 0.1, 0.1

# Максимальное время и общее количество
# временных точек:
tmax, n = 500, 30000

# Интегрируем систему уравнений в каждой точке
# временного интервала t:
t = np.linspace(0, tmax, n)
f = odeint(WangSunAttractor, (x_0, y_0, z_0), t,
           args=(alpha, beta, zeta, delta, epsilon, xi))

В заключение

Огонь, вода, земля, небо, солнце, луна, звезды — все это самые древние поэтические сущности. Очень часто, мне удается найти в математике, что-то такое же прекрасное. Но гораздо чаще, я даже не понимаю, как обо всем этом говорить на математическом языке и языке обычном. Не понимаю, но хочется научиться.

Но вот, что я осознал на все 100%, так это то, что современные инструменты визуализации дают фантастическую возможность выразить свое отношение к тому чем ты сейчас занят, возможность показать, как это важно для тебя и как тебе это интересно. Сделать все это без слов.

© Habrahabr.ru