Вероятностные модели: LDA, часть 2
Продолжаем разговор. В прошлый раз мы сделали первый шаг на переходе от наивного байесовского классификатора к LDA: убрали из наивного байеса необходимость в разметке тренировочного набора, сделав из него модель кластеризации, которую можно обучать ЕМ-алгоритмом. Сегодня у меня уже не осталось отговорок — придётся рассказывать про саму модель LDA и показывать, как она работает. Когда-то мы уже говорили об LDA в этом блоге, но тогда рассказ был совсем короткий и без весьма существенных подробностей. Надеюсь, что в этот раз удастся рассказать больше и понятнее. LDA: интуицияИтак, начинаем разговор об LDA. Напомню, что основная цель нашего обобщения — добиться того, чтобы документ не был жёстко привязан к одной теме, и слова в документах могли приходить из нескольких тем сразу. Что это значит в (математической) реальности? Это значит, что документ представляет собой смесь из тем, и каждое слово может быть порождено из одной из тем в этой смеси. Проще говоря, мы сначала кидаем кубик-документ, определяя тему для каждого слова, а потом вытаскиваем слово из соответствующего мешка.Таким образом, основная интуиция модели выглядит примерно так:
LDA: интуицияИтак, начинаем разговор об LDA. Напомню, что основная цель нашего обобщения — добиться того, чтобы документ не был жёстко привязан к одной теме, и слова в документах могли приходить из нескольких тем сразу. Что это значит в (математической) реальности? Это значит, что документ представляет собой смесь из тем, и каждое слово может быть порождено из одной из тем в этой смеси. Проще говоря, мы сначала кидаем кубик-документ, определяя тему для каждого слова, а потом вытаскиваем слово из соответствующего мешка.Таким образом, основная интуиция модели выглядит примерно так:
на свете бывают темы (заранее неизвестные), которые отражают то, о чём могут быть части документа; каждая тема — это распределение вероятностей на словах, т.е. мешок слов, из которого можно с разной вероятностью вытащить разные слова; каждый документ — это смесь тем, т.е. распределение вероятностей на темах, кубик, который можно кинуть; процесс порождения каждого слова состоит в том, чтобы сначала выбрать тему по распределению, соответствующему документу, а затем выбрать слово из распределения, соответствующего этой теме. Поскольку интуиция — это самое главное, и здесь она не самая простая, повторю ещё раз то же самое другими словами, теперь чуть более формально. Вероятностные модели удобно понимать и представлять в виде порождающих процессов (generative processes), когда мы последовательно описываем, как порождается одна единица данных, вводя по ходу дела все вероятностные предположения, которые мы в этой модели делаем. Соответственно, порождающий процесс для LDA должен последовательно описывать, как мы порождаем каждое слово каждого документа. И вот как это происходит (здесь и далее я буду предполагать, что длина каждого документа задана — её тоже можно добавить в модель, но обычно это ничего нового не даёт):
для каждой темы t: выбрать вектор φt (распределение слов в теме) по распределению 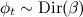 ;
для каждого документа d: выбрать вектор
;
для каждого документа d: выбрать вектор 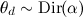 — вектор «степени выраженности» каждой темы в этом документе;
для каждого из слов документа w: выбрать тему zw по распределению
— вектор «степени выраженности» каждой темы в этом документе;
для каждого из слов документа w: выбрать тему zw по распределению 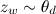 ;
выбрать слово
;
выбрать слово 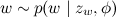 с вероятностями, заданными в β.
Здесь процесс выбора слова при данных θ и φ уже должен быть читателю понятен — мы для каждого слова кидаем кубик и выбираем тему слова, потом вытаскиваем само слово из соответствующего мешка:
с вероятностями, заданными в β.
Здесь процесс выбора слова при данных θ и φ уже должен быть читателю понятен — мы для каждого слова кидаем кубик и выбираем тему слова, потом вытаскиваем само слово из соответствующего мешка:

В модели осталось объяснить только то, откуда же берутся эти θ и φ и что означает выражение 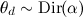 ; заодно объяснится и то, почему это называется Dirichlet allocation.
; заодно объяснится и то, почему это называется Dirichlet allocation.
При чём тут Дирихле?
Иоганн Петер Густав Лежён Дирихле не так уж много занимался теорией вероятностей; он в основном специализировался на матанализе, теории чисел, рядах Фурье и другой тому подобной математике. В теории вероятностей он был не так уж часто замечен, хотя, конечно, его результаты в теории вероятностей сделали бы блестящую карьеру современному математику (деревья были зеленее, науки были менее исследованы, и, в частности, математический Клондайк тоже ещё не истощился). Однако в своих исследованиях математического анализа Дирихле, в частности, сумел взять вот такой классический интеграл, который в результате получил название интеграла Дирихле: 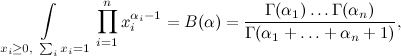 где Γ (αi) — это гамма-функция, продолжение факториала (для натуральных чисел
где Γ (αi) — это гамма-функция, продолжение факториала (для натуральных чисел 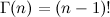 ). Сам Дирихле вывел этот интеграл для нужд небесной механики, затем Лиувилль нашёл более простой вывод, который обобщался и на более сложные формы подинтегральных функций, и всё заверте.Распределение Дирихле, мотивированное интегралом Дирихле, — это распределение на (n-1)-мерном векторе x1, x2, …, xn-1, заданное таким образом:
). Сам Дирихле вывел этот интеграл для нужд небесной механики, затем Лиувилль нашёл более простой вывод, который обобщался и на более сложные формы подинтегральных функций, и всё заверте.Распределение Дирихле, мотивированное интегралом Дирихле, — это распределение на (n-1)-мерном векторе x1, x2, …, xn-1, заданное таким образом: 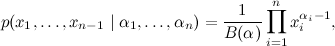 где
где 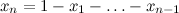 , и распределение задано только на (n-1)-мерном симплексе, где xi>0. Из интеграла Дирихле в нём появилась нормировочная константа. И смысл распределения Дирихле довольно изящный — это распределение на распределениях. Посмотрите — в результате набрасывания вектора по распределению Дирихле получается вектор с неотрицательными элементами, сумма которых равна единице… ба, да это же дискретное распределение вероятностей, фактически нечестный кубик с n гранями.
, и распределение задано только на (n-1)-мерном симплексе, где xi>0. Из интеграла Дирихле в нём появилась нормировочная константа. И смысл распределения Дирихле довольно изящный — это распределение на распределениях. Посмотрите — в результате набрасывания вектора по распределению Дирихле получается вектор с неотрицательными элементами, сумма которых равна единице… ба, да это же дискретное распределение вероятностей, фактически нечестный кубик с n гранями.
Конечно, это не единственный возможный класс распределений на дискретных вероятностях, но распределение Дирихле обладает и рядом других привлекательных свойств. Главное — оно является сопряжённым априорным распределением для того самого нечестного кубика; я сейчас не буду подробно объяснять, что это значит (возможно, потом), но, в общем, именно распределение Дирихле разумно брать в качестве априорного распределения в вероятностных моделях, когда в качестве переменной хочется получить нечестный кубик.
Осталось обсудить, что, собственно, будет получаться для разных значений αi. Прежде всего давайте сразу ограничимся случаем, когда все αi одинаковые — у нас априори нет никакой причины предпочитать некоторые темы другим, мы в начале процесса ещё и не знаем, где какие темы выделятся. Поэтому распределение наше будет симметричным.
Что вообще значит — распределение на симплексе? Как оно выглядит? Давайте нарисуем несколько таких распределений — нарисовать мы можем максимум в трёхмерном пространстве, так что симплекс будет двумерный — треугольник, проще говоря, — и распределение будет над этим треугольником (картинка взята отсюда; в принципе понятно, о чём там идёт речь, но очень интересно, почему под ящиком Пандоры подписано Uniform (0,1) — если кто-нибудь понимает, расскажите:)): 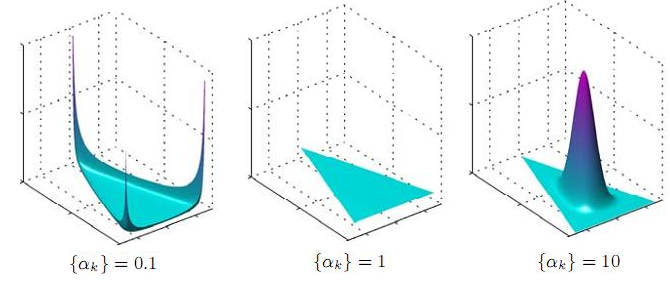 А вот аналогичные распределения в двумерном формате, в виде heatmap’ов (как их можно нарисовать, объяснено, например, здесь); правда, тут 0.1 было бы совершенно не видно, так что я заменил на 0.995:
А вот аналогичные распределения в двумерном формате, в виде heatmap’ов (как их можно нарисовать, объяснено, например, здесь); правда, тут 0.1 было бы совершенно не видно, так что я заменил на 0.995: 
И вот что получается: если α=1, получается равномерное распределение (что и логично — тогда все степени в функции плотности равны нулю). Если α больше единицы, то с дальнейшим увеличением α распределение всё больше и больше сосредотачивается в центре симплекса. При больших α мы будем почти всегда получать почти совсем честные кубики. Но самое интересное здесь в том, что происходит, когда α меньше единицы — в этом случае распределение сосредотачивается в углах и на рёбрах/сторонах симплекса! Иначе говоря, для маленьких α мы будем получать разреженные кубики — распределения, в которых почти все вероятности равны или близки к нулю, и лишь небольшая их часть существенно ненулевые. Это ровно то, что нам нужно — и в документе нам хотелось бы видеть немного существенно выраженных тем, и тему было бы хорошо достаточно чётко очертить относительно небольшим подмножеством слов. Поэтому в LDA обычно берут гиперпараметры α и β меньше единицы, обычно α=1/T (обратное к числу тем) и β=Const/W (константа вроде 50 или 100 разделить на число слов).
Disclaimer: моё изложение следует самому простому и прямолинейному подходу к LDA, я пытаюсь крупными мазками передать общее понимание модели. На самом же деле, конечно, есть и более детальные исследования о том, как следует выбирать гиперпараметры α и β, что они дают и к чему приводят; в частности, гиперпараметры вовсе не обязаны быть симметричными. См., например, статью Wallach, Nimho, McCallum «Rethinking LDA: Why Priors Matter».
LDA: граф, совместное распределение, факторизация
Подведём краткий итог. Мы уже объяснили все части модели — априорное распределение Дирихле производит кубики-документы и мешки-темы, бросанием кубика-документа определяется своя тема для каждого слова, а затем само слово выбирается из соответствующего мешка-темы. Формально говоря, получается, что графическая модель выглядит так: 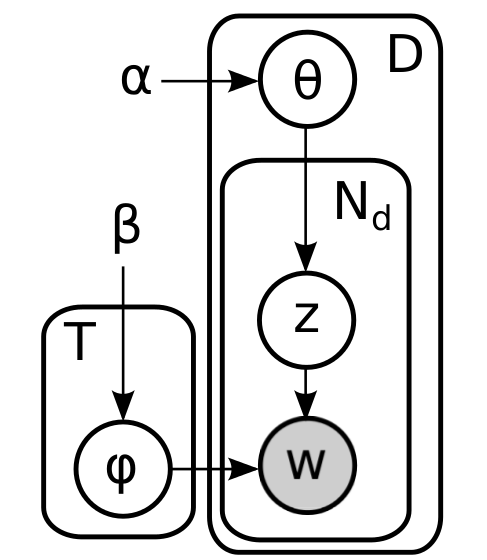 Здесь внутренняя плашка соответствует словам одного документа, а внешняя плашка — документам в корпусе. Не нужно обманываться внешней простотой этой картинки, циклов здесь более чем достаточно; вот, например, полностью развёрнутый фактор-граф для двух документов, в одном из которых два слова, а в другом три:
Здесь внутренняя плашка соответствует словам одного документа, а внешняя плашка — документам в корпусе. Не нужно обманываться внешней простотой этой картинки, циклов здесь более чем достаточно; вот, например, полностью развёрнутый фактор-граф для двух документов, в одном из которых два слова, а в другом три:  И совместное распределение вероятностей, получается, факторизуется так:
И совместное распределение вероятностей, получается, факторизуется так: 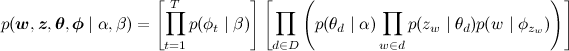
Что такое теперь задача обучения модели LDA? Получается, что нам даны только слова, больше не дано ничего, и надо как-нибудь обучить все-все-все эти параметры. Задача выглядит очень страшно — ничего не известно и всё надо вытащить из набора документов: 
Тем не менее она решается при помощи тех самых методов приближённого вывода, о которых мы говорили раньше. В следующий раз мы поговорим о том, как же решать эту задачу, применим метод сэмплирования по Гиббсу (см. одну из предыдущих инсталляций) к модели LDA и выведем уравнения апдейта для переменных zw; мы увидим, что на самом деле вся эта страшная математика совсем не такая страшная, а LDA вполне доступно пониманию не только концептуально, но и алгоритмически.
