Вейвлет – анализ. Основы26.04.2019 20:04

Введение

Английское слово wavelet (от французского «ondelette») дословно переводится как «короткая (маленькая) волна». В различных переводах зарубежных статей на русский язык встречаются еще термины: «всплеск», «всплесковая функция», «маловолновая функция», «волночка» и др.

Вейвлет-преобразование (ВП) широко используется для анализа сигналов. Помимо этого, оно находит большое применение в области сжатия данных. ВП одномерного сигнала — это его представление ввиде обобщенного ряда или интеграла Фурье по системе базисных функций.

$\psi _{ab}(t)=\frac{1}{\sqrt{a}}\psi \left ( \frac{t-b}{a} \right )$ , (1)

сконструированных из материнского (исходного) вейвлета $\psi(t)$ , обладающего определенными свойствами за счет операций сдвига во времени (b) и изменения временного масштаба (a).

Множитель $1/\sqrt{a}$ обеспечивает независимость нормы функций (1) от масштабирующего числа (a). Для заданных значений параметров a и b функция $\psi_{ab}(t)$ и есть вейвлет, порождаемый материнским вейвлетом $\psi(t)$ .

В качестве примера приведём вейвлет «мексиканская шляпа» во временной и частотной областях:

Листинг вейвлета для временной области

from numpy import*
import matplotlib.pyplot as plt
x= arange(-4,30,0.01)
def w(a,b,t):    
    f =(1/a**0.5)*exp(-0.5*((t-b)/a)**2)* (((t-b)/a)**2-1)
    return f
plt.title("Вейвлет «Мексиканская шляпа»:\n$1/\sqrt{a}*exp(-0,5*t^{2}/a^{2})*(t^{2}-1)$")
y=[w(1,0,t) for t in x]
plt.plot(x,y,label="$\psi(t)$ a=1,b=12") 
y=[w(2,12,t) for t in x]
plt.plot(x,y,label="$\psi_{ab}(t)$ a=2 b=12")   
y=[w(4,12,t) for t in x]
plt.plot(x,y,label="$\psi_{ab}(t)$ a=4 b=12")   
plt.legend(loc='best')
plt.grid(True)
plt.show()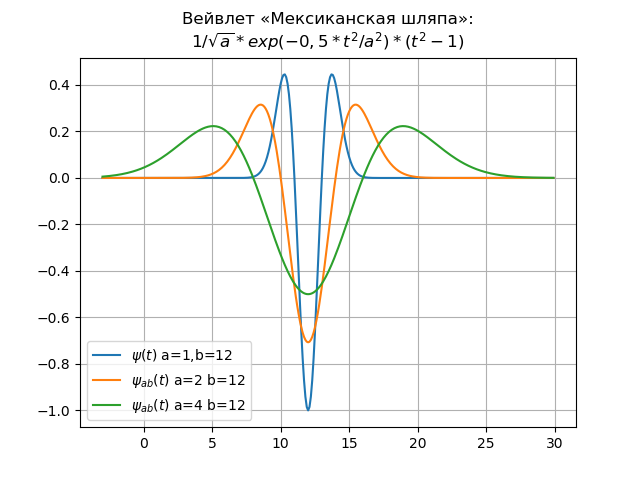

Листинг для спектра вейвлета

from numpy import*
from pylab import *
from scipy import *
import os
def w(a,b,t):    
    f =(1/a**0.5)*exp(-0.5*((t-b)/a)**2)* (((t-b)/a)**2-1)
    return f
x= arange(-4,30,0.2)
def plotSpectrum(y,Fs):
 n = len(y) 
 k = arange(n)
 T = n/Fs
 frq = k/T
 frq = frq[range(int(n/2))] 
 Y = fft(y)/n 
 Y = Y[range(int(n/2))]
 return Y,frq 
 xlabel('f (Hz)')
 ylabel('|Y(f)|')
Fs=1024.0
y=[w(1,12,t) for t in x]
Y,frq=plotSpectrum(y,Fs)
plot(frq,abs(Y),label="$\psi(\omega)$ a=1,b=12")
y=[w(2,12,t) for t in x]
Y,frq=plotSpectrum(y,Fs)
plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=2 b=12")
y=[w(4,12,t) for t in x]
Y,frq=plotSpectrum(y,Fs)
plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=4 b=12")
plt.title("Вейвлет «Мексиканская шляпа» частотная область $\omega$")
legend(loc='best')
grid(True)
show()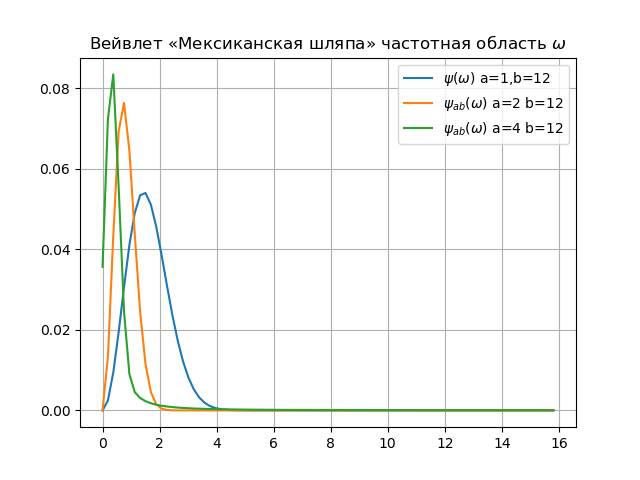

Вывод:
1.Между концепцией гармоник Фурье и масштабом вейвлета действительно существует взаимосвязь. Главное в этой взаимосвязи — обратная пропорциональность собственной частоты и масштаба. Кроме этого, уменьшая масштаб, мы увеличиваем полосу пропускания спектра вейвлета.

2. За счет изменения масштаба (увеличение a приводит к сужению фурье-спектра функции $\psi_{ab}(t)$ ), вейвлеты способны выявлять различие в характеристиках на разных шкалах (частотах), а за счет сдвига- проанализировать свойства сигнала в разных точках на всем исследуемом интервале. Поэтому, при анализе нестационарных сигналов, за счет свойства локальности вейвлетов, получают существенное преимущество перед преобразованием Фурье, которое дает только глобальные сведения о частотах (масштабах) анализируемого сигнала, так как используемая при этом система функций (комплексная экспонента или синусы и косинусы) определена на бесконечном интервале.

3. Приведенные листинги, написанные на свободно распространяемом языке высокого уровня Python позволяют подбирать функции для вейвлетов, отвечающие заданным требованиям. Однако, при этом дополнительно необходимо учесть все главные признаки вейвлетов.

Главные признаки вейвлета

Ограниченность. Квадрат нормы функции должен быть конечным:
$\left \| \psi \right \|^{2}=\int_{-\infty }^{\infty }\left | \psi (t) \right |^{2}dt< \infty$ . (2)

Локализация. ВП в отличие от преобразования Фурье использует локализованную исходную функцию и во времени, и по частоте. Для этого достаточно, чтобы выполнялись условия:

$\left | \psi (t) \right |\leq C(1+\left | t \right |)^{-1-\varepsilon }$ и
$\left | S_{\psi }(\omega ) \right |\leq C(1+\left | \omega \right |)^{-1-\varepsilon }$ при $$\varepsilon > 0$» />, (3)</p> <p>Например, дельта-функция <img src=$ и гармоническая функция не удовлетворяют необходимому условию одновременной локализации во временной и частотной областях.

Нулевое среднее. График исходной функции должен осциллировать (быть знакопеременным) вокруг нуля на оси времени и иметь нулевую площадь:

$\int_{-\infty }^{\infty }\psi (t)dt=0$ . (4)

Из этого условия становится понятным выбор названия «вейвлет» — маленькая волна.

Равенство нулю площади функции $\psi(t)$ , т.е. нулевого момента, приводит к тому, что фурье-преобразование $S_{\psi}(\omega)$ этой функции равно нулю при $\omega =0$ и имеет вид полосового фильтра. При различных значениях (a) это будет набор полосовых фильтров.

Часто для приложений бывает необходимо, чтобы не только нулевой, но и все первые n моментов были равны нулю:

$\int_{-\infty }^{\infty }t^{^{n}}\psi (t)dt=0$ . (5)

Вейвлеты n -го порядка позволяют анализировать более тонкую (высокочастотную) структуру сигнала, подавляя медленно изменяющиеся его составляющие.

Автомодельность. Характерным признаком ВП является его самоподобие. Все вейвлеты конкретного семейства $\psi_{ab}(t)$ имеют то же число осцилляций, что и материнский вейвлет $\psi(t)$ , поскольку получены из него посредством масштабных преобразований (a) и сдвига (b).

Непрерывное вейвлет-преобразование

Непрерывное (интегральное) вейвлет-преобразование (НВП или СWT — continuous wavelet transform). Сконструируем базис $\psi_{ab}(t)$ с помощью непрерывных масштабных преобразований (a) и переносов (b) материнского вейвлета $\psi(t)$ с произвольными значениями базисных параметров a и b в формуле (1).

Тогда, по определению прямое (анализ) и обратное (синтез) HВП (т.е. ПНВП и ОНВП) сигнала S (t) запишутся так:
$W_{s}(a,b)=(S(t),\psi _{ab}(t))=\frac{1}{\sqrt{a}}\int_{-\infty }^{\infty }S(t)\psi \left ( \frac{t-b}{a} \right )dt$ , (6)

$S(t)=\frac{1}{C_{\psi }}\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }W_{s}(a,b)\psi _{ab}(t)\frac{dadb}{a^{2}}$ , (7)

где $C_{\psi }$ — нормирующий коэффициент,
$C_{\psi }=\int_{-\infty }^{\infty }\left | \psi (\omega ) \right |^{2}\left | \omega \right |^{-1}d\omega < \infty$
где: (•, •) — скалярное произведение соответствующих сомножителей,
$\mathbf{\psi(\omega)}$ — фурье-преобразование вейвлета $\psi(t)$ . Для ортонормированных вейвлетов $C_{\psi } = 1$ .

Из (6) следует, что вейвлет-спектр $W_{s}(b,a)$ (wavelet spectrum, или time-scale-spectrum — масштабно-временной спектр) в отличие от фурье-спектра (single spectrum) является функцией двух аргументов: первый аргумент, а (временной масштаб) аналогичен периоду осцилляций, т.е. обратен частоте, а второй b–аналогичен смещению сигнала по оси времени.

Следует отметить, что $W_{s}(b,a_{0})$ характеризует временную зависимость (при $a=a_{0})$ , тогда как зависимости $W_{s}(a,b_{0})$ можно поставить в соответствие частотную зависимость (при $b=b_{0}$ ).

Если исследуемый сигнал S (t) представляет собой одиночный импульс длительностью $\tau_{u}$ , сосредоточенный в окрестности $t=t_{0}$ , то его вейвлет-спектр будет иметь наибольшее значение в окрестности точки с координатами $a=\tau_{u},b=t_{0}$ .

Способы представления (визуализации) $W_{s}(b,a)$ могут быть различными. Спектр $W_{s}(b,a)$ является поверхностью в трехмерном пространстве. Однако, часто вместо изображения поверхности представляют её проекцию на плоскость ab с изоуровнями (или фигурами различных цветов), позволяющими проследить изменение интенсивности амплитуд ВП на разных масштабах (а) и во времени (b).

Кроме того, изображают картины линий локальных экстремумов этих поверхностей, так называемый скелетон (sceleton), который выявляет структуру анализируемого сигнала.

Непрерывное вейвлет преобразование при определении вейвлет спектра на основе материнского вейвлета -«мексиканская шляпа».

Применяются и другие материнские вейвлеты используемые для НВП:

Непрерывное ВП нашло широкое применение в обработке сигналов. В частности, вейвлет-анализ (ВА) дает уникальные возможности распознавать локальные и «тонкие» особенности сигналов (функций), что важно во многих областях радиотехники, связи, радиоэлектроники, геофизики и других отраслях науки и техники. Рассмотрим эту возможность на некоторых простейших примерах.

Гармоническое колебание.

Сигнал имеет вид: $s(t)=Asin(\omega t-\phi)$

где: $A=1 V,\omega=\frac{2\pi }{T}=\frac{2\pi }{50},\psi=0$

Вейвлетобразующая функция: $MHAT(t):=\frac{d^{2}}{dt^{2}}exp(-t^{2}/2)$ ,

Вейвлеты: $\psi (a,b,t)=\frac{1}{\sqrt{a}}MHAT\left ( \frac{t-b}{a} \right )$ ,

Вейвлет-спектр: N:=256, a:=1…30, b:=0…50, $W(a,b):=\int_{-N}^{N}\psi (a,b,t)s(t)dt, N_{ab}:=W(a,b).$ .

Листинг программы

from scipy.integrate import quad
from numpy import*
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
N=256
T=50
def S(t):
    return sin(2*pi*t/T)
plt.figure()
plt.title(' Гармоническое колебание', size=12)
y=[S(t) for t in arange(0,100,1)]
x=[t for t in arange(0,100,1)]
plt.plot(x,y)
plt.grid()
def w(a,b):    
    f = lambda t :(1/a**0.5)*exp(-0.5*((t-b)/a)**2)* (((t-b)/a)**2-1)*S(t)
    r= quad(f, -N, N)
    return round(r[0],3)
x = arange(1,50,1)
y = arange(1,50,1)
z = array([w(i,j) for j in y for i in x])
X, Y = meshgrid(x, y)
Z = z.reshape(49,49)
fig = plt.figure("Вейвлет- спектр: гармонического колебания")
ax = Axes3D(fig)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet)
ax.set_xlabel(' Масштаб:a')
ax.set_ylabel('Задержка: b')
ax.set_zlabel('Амплитуда ВП: $ N_{ab}$')
plt.figure("2D-график для z = w (a,b)")
plt.title('Плоскость ab с цветовыми областями ВП', size=12)
plt.contourf(X, Y, Z,100)
plt.show()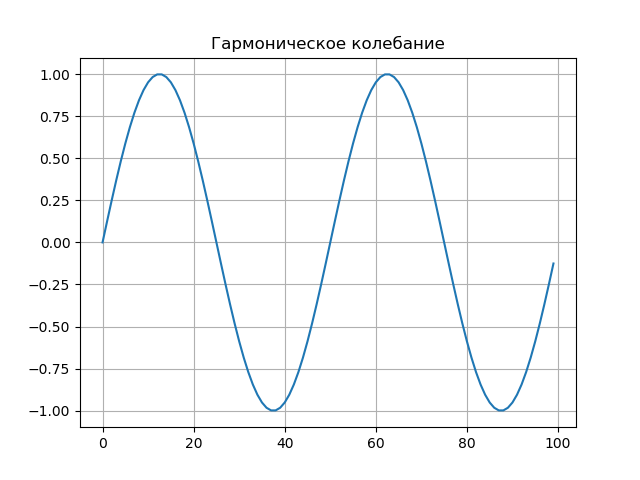

График сигнала.

График двухпараметрического спектра $N_{ab}=W(ab)$ выведен в виде поверхности в трехмерном пространстве.

Следует отметить, что сечение W (a, b) для временного масштаба $a=a_{0}$ характеризует исходное колебание s (t). При этом амплитуда его максимальна при $a_{0}:1/\omega$ . Зависимости $W(a_{0},b_{0})$ можно поставить в соответствие текущий спектр колебания при $b=b_{0}$ .

Сумма двух гармонических колебаний.

Сигнал имеет вид : $s(t):=A_{1}sin(\omega _{1}t)+A_{2}sin(\omega _{2}t)$

где: $A_{1}=A_{2}=1V,\omega_{1}=\frac{2\pi}{T_{1}},\omega_{2}=\frac{2\pi }{T_{2}},T_{1}=50s,T_{2}=10s$ .

$MHAT(t):=\frac{d^{2}}{dt^{2}}\left [ e^{-t^{2/2}} \right ]$ , N:=256,
$\psi (a,b,t):=MHAT\left ( \frac{t-b}{a} \right ), W(a,b):=\int_{-N}^{N}\psi (a,b,t)f(t)dt$ , a:=1…30, b:=0…50, $N_{ab}:=W(a,b)$ .

Листинг программы

from scipy.integrate import quad
from numpy import*
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
N=256
def S(t):
    return sin(2*pi*t/10)+sin(2*pi*t/50)
plt.figure(' Сумма двух гармонических колебаний')
plt.title(' Сумма двух гармонических колебаний', size=12)
y=[S(t) for t in arange(0,250,1)]
x=[t for t in arange(0,250,1)]
plt.plot(x,y)
plt.grid()
def w(a,b):    
    f = lambda t :(1/a**0.5)*exp(-0.5*((t-b)/a)**2)* (((t-b)/a)**2-1)*S(t)
    r= quad(f, -N, N)
    return round(r[0],3)
x = arange(1,50,1)
y = arange(1,50,1)
z = array([w(i,j) for j in y for i in x])
X, Y = meshgrid(x, y)
Z = z.reshape(49, 49)
fig = plt.figure("Вейвлет-спектр:2-х гармонических колебаний")
ax = Axes3D(fig)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet)
ax.set_xlabel(' Масштаб:a')
ax.set_ylabel('Задержка: b')
ax.set_zlabel('Амплитуда ВП: $ N_{ab}$')
plt.figure("2D-график для z = w (a,b)")
plt.title('Плоскость ab с цветовыми областями ВП', size=12)
plt.contourf(X, Y, Z, 100)
plt.figure()
q=[w(2,i) for i in y]
p=[i for i in y]
plt.plot(p,q,label='w(2,b)')
q=[w(15,i) for i in y]
plt.plot(p,q,label='w(15,b)')
q=[w(30,i) for i in y]
plt.plot(p,q,label='w(30,b)')
plt.legend(loc='best')
plt.grid(True)
plt.figure()
q=[w(i,13) for i in x]
p=[i for i in x]
plt.plot(p,q,label='w(a,13)')
q=[w(i,17) for i in x]
plt.plot(p,q,label='w(a,17)')
plt.legend(loc='best')
plt.grid(True)
plt.show()

График сигнала.

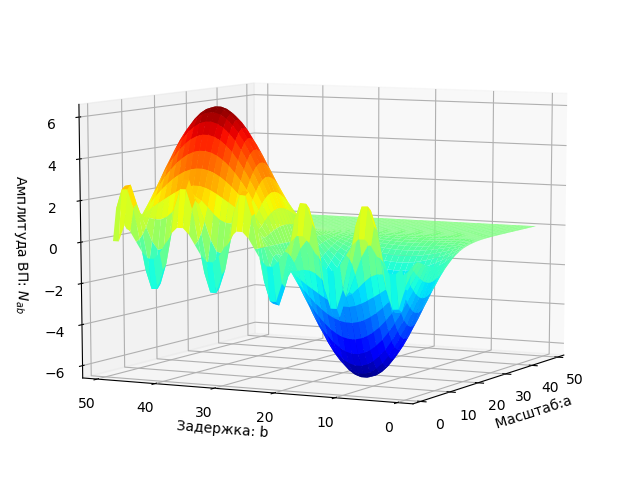
График двухпараметрического спектра W (a, b) выведен виде поверхности в трехмерном пространстве.

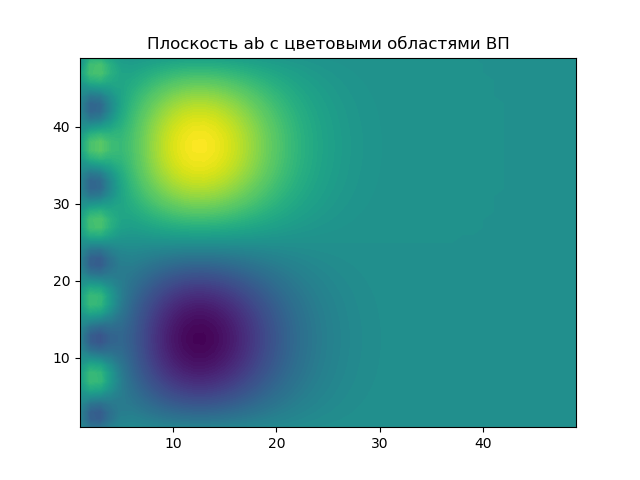
Плоскость параметров a, b на которой результаты ВП выделены цветными областями.

На графике приведены «сечения» вейвлет-спектра для двух значений параметра а. При относительно небольшом параметре временного масштаба a, при $a_{1}=2(a_{1}:1/\omega_{2})$ , сечение спектра несет информацию только о высокочастотной составляющей сигнала, отфильтровывая (подавляя) его низкочастотный компонент.

С ростом a происходит растяжение базисной функции $\psi(\frac{t-b}{a})$ , следовательно, сужение ее спектра, и сужению полосы пропускания частотного «окна». В результате при $a_{2}=15(a_{2}:1/\omega_{1})$ сечение спектра представляет собой лишь низкочастотный компонент сигнала.

При дальнейшем увеличении a полоса окна еще уменьшается и уровень этого низкочастотного компонента убывает до постоянной составляющей (при a >25), равной нулю для анализируемого сигнала.

На графике приведены сечения вейвлет-спектра W (a, b), характеризующие
текущий спектр сигнала при $b_{1}=13$ и $b_{2}=17$ . Спектр рассматриваемого сигнала в отличие от гармонического содержит высокочастотный компонент в области малых значений временного масштаба a (a:1…3), который соответствует второй составляющей сигнала $A_{2}sin(\omega_{2}t)$ .

Прямоугольный импульс.

$U:=5,t_{0}:=20, \tau :=60$
$s(t):=\begin{vmatrix}U, if t_{0}\leq t\leq t_{0}+\tau \\ 0, otherwise \end{vmatrix}$
$MHAT (t):=\frac{d^{2}}{dt^{2}}exp\left ( \frac{-t^{2}}{2} \right )$
$N:=128,\psi (a,b,t):=MHAT\left ( \frac{t-b}{a} \right ), W(a,b):=\int_{-N}^{N}\psi (a,b,t)f(t)dt$
$a:=1..50, b:=0..100, N_{ba}:=W(a,b)$

Листинг программы

from scipy.integrate import quad
from numpy import*
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
N=256
def S(t):
    U=5;t0=20;tau=60
    if  t0<=t<=t0+tau:
        return U
    else:
        return 0
plt.figure()
plt.title('Прямоугольный импульс', size=12)
y=[S(t) for t in arange(0,120,1)]
x=[t for t in arange(0,120,1)]
plt.plot(x,y)
plt.grid()
def w(a,b):    
    f = lambda t :(1/a**0.5)*exp(-0.5*((t-b)/a)**2)* (((t-b)/a)**2-1)*S(t)
    r= quad(f, -N, N)
    return round(r[0],3)
x = arange(1,100,1)
y = arange(1,100,1)
z = array([w(i,j) for j in y for i in x])
X, Y = meshgrid(x, y)
Z = z.reshape(99, 99)
fig = plt.figure("3D-график вейвлет спектрограммы")
ax = Axes3D(fig)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet)
ax.set_xlabel(' Масштаб:a')
ax.set_ylabel('Задержка: b')
ax.set_zlabel('Амплитуда ВП: $ N_{ab}$')
plt.figure("2D-график для z = w (a,b)")
plt.title('Плоскость ab с цветовыми областями ВП', size=12)
plt.contourf(X, Y, Z,100)
plt.show()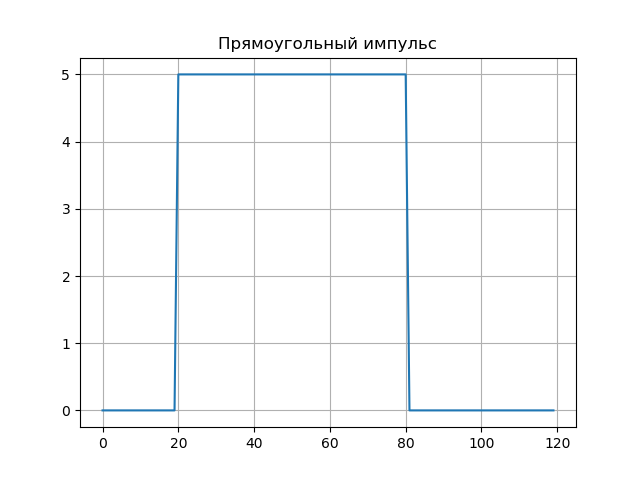

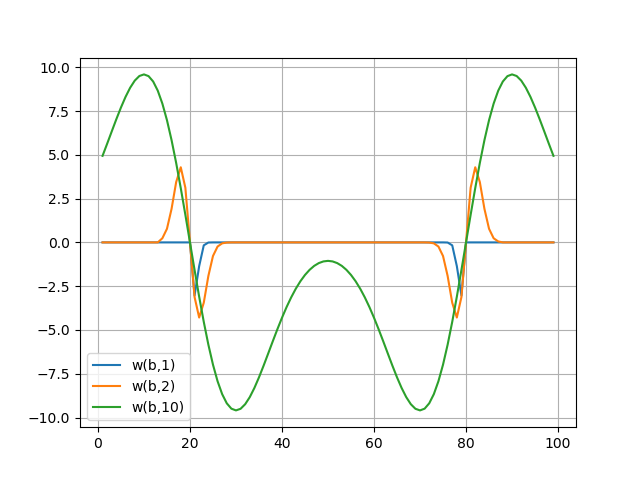
Вейвлет-спектры приведены в графиках, вейвлет-спектр хорошо передает тонкие особенности сигнала — его скачки на отсчетах b =20 и b =80 (при a:1…10).

Выводы:

Эта публикация носит учебный характер, в ней приведены основные сведения о вейвлет- анализе в целом, а на простых примерах на свободно распространяемом высокоуровневом языке программирования Python показаны особенности непрерывного вейвлет-анализа с обширной графической 3D и 2D визуализацией.

P.S. Автор не умоляет безусловные преимущества вейвлет-анализа с применением Matlab как по количеству вейвлетов, так и по быстродействию. Но на Python есть ещё куда развиваться- это scipy.signal и PyWavelets.