В тени случайного леса
1. Вступление
Это небольшой рассказ о практических вопросах использования машинного обучения для масштабных статистических исследований различных данных в Интернет. Также будет затронута тема применения базовых методов математической статистики для анализа данных.
2. Классификация асессором
Асессор очень часто сталкивается с нормально распределёнными наборами данных. Существует правило, согласно которому при нормальном распределении (его называют распределением Гаусса) случайная величина крайне редко отклоняется более чем на три сигмы (греческой буквой «сигма» обозначают квадратный корень из дисперсии, т.е. среднеквадратическое отклонение) от своего математического ожидания. Другими словами: при нормальном распределении большинство объектов будут мало отличаться от среднего. Следовательно, гистограмма будет иметь следующий вид:

Такая случайная величина может коррелировать с другой величиной и даже образовывать группы (кластеры) по некоторым признакам схожести. Рассмотрим небольшой пример. Допустим, что мы располагаем информацией о массе и высоте объекта, а также знаем, что в генеральной совокупности бывают объекты только двух классов (велосипед и грузовик). Очевидно, что высота и масса грузовика явно больше, чем у велосипеда, следовательно, оба показателя невероятно ценны для классификации.
Если мы отобразим в двумерном пространстве облако точек, координаты которых заданы исследуемой парой множеств, то будет очевидно, что точки не распределены случайным образом, а собираются в группы (кластеры). Следовательно, пространство можно разделить линей (гиперплоскостью), которая позволит отличить грузовые машины от велосипедов (например, если масса более 1000 кг, то это явно грузовик).
Более того, можно зафиксировать линейную зависимость между этими метриками (при увеличении позиции по ординате происходит явное увеличение по абсциссе). Таким образом, точки выстраиваются в ряд от левого нижнего угла к правому верхнему углу, словно вокруг натянутой нити. Для большей наглядности добавим (методом наименьших квадратов) прямую линию регрессионного анализа, отметим центродиды кластеров, а также отобразим графики этих переменных:
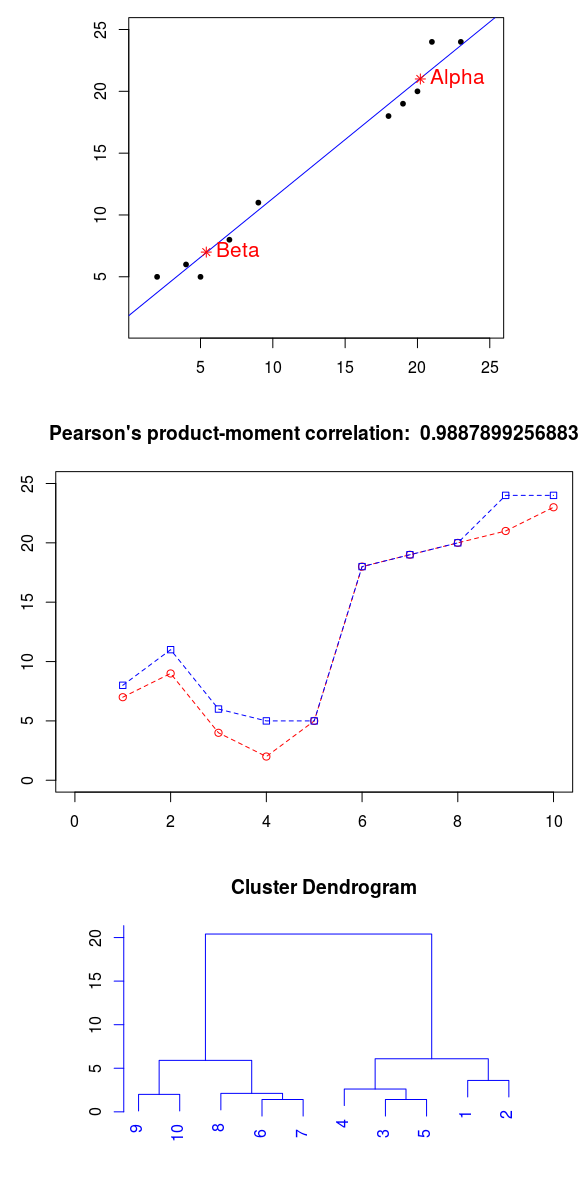
Используя имеющиеся данные, вычислим степень взаимосвязи. Для подобных наборов данных в математической статистики применяют линейный коэффициент корреляции Карла Пирсона. Это достаточно удобно, так как он находится в интервале от -1 до 1. Чтобы его вычислить необходимо разделить ковариацию на произведение среднеквадратических отклонений множеств (квадратный корень из дисперсии). Кстати, ковариация не изменится, если поменять местами сравниваемые множества, а если они будут одинаковы, то мы получим дисперсию случайной величины. Важно отметить, что зависимость должна быть строго линейной.

Однако, существует ещё ряд других независимых переменных (предикторы), которые влияют на зависимую (критериальную) переменную. Нет функциональной зависимости, которая позволила бы по формуле вычислить одну переменную, зная другую. Например, это как зависимость роста человека от веса (зависимость существует, но нет формулы, которая позволит зная только вес точно вычислить рост). А как действовать, если очень много переменных и необходимо оценить важность каждой из них?
Одним из подходов к решению этой задачи можно назвать применение алгоритмов машинного обучения. Так, например, алгоритм CART (был разработан ещё в начале 80-х годов XX века учёными Лео Брейманом, Джеромом Фридманом, Чарлзом Стоуном и Ричардом Олшеном) позволит достаточно хорошо отобразить деревья решений. Естественно, он предполагает, что все векторы признаков уже размечены асессором. Однако, для более сложных задач чаще применяют Random forest или Gradient Boosting. Используя упомянутые методы (а также логистическую регрессию) визуально отобразим степень важности каждой переменой:

Естественно, выбор методов напрямую зависит от поставленной задачи и специфики набора данных. Но в подавляющем большинстве задач автоматическая классификация начинается с предварительного анализа данных. Вполне вероятно, что асессоры и эксперты смогут увидеть важные закономерности просто изучая визуальное представление данных и показатели описательной статистики (корреляция, минимальное значение, максимальное значение, среднее значение, медиана, квартили, дисперсия).
3. Автоматическая классификация
По сути, вместо конкретного объекта (сайт, человек, машина, самолёт) мы сталкиваемся с набором его характеристик (масса, скорость, наличие USB). Это значит, что происходит процесс превращения сущности в вектор признаков. Так как же быть с действительно сложными наборами данных?
Единого подхода не может существовать, так как есть очень много специфических требований. Для автоматического распознавания изображения нужны одни алгоритмы (например, искусственные нейронные сети), а для сложного лингвистического анализа текста нужны совсем другие.
В подавляющем большинстве случаев машинное обучение начинается с предварительной очистки данных. На этом этапе может происходить удаление заведомо неподходящих объектов и более простые способы классификации. В следующем примере происходит поиск центроидов двух кластеров. В качестве конкретной реализации будет выступать достаточно популярное решение (недавно опубликованная вторая версия Apache Spark).
import org.apache.spark.mllib.clustering.{KMeans, KMeansModel}
import org.apache.spark.mllib.linalg.Vectors
val data = sc.textFile(clusterDataFile).map(s => Vectors.dense(s.split(',').map(_.toDouble))).cache()
KMeans.train(data, 2, 100).clusterCenters.map(h => h(0) + "," + h(1)).mkString("\n")С увеличением сложности задачи растёт и сложность систем машинного обучения. Так, например, некоторые поисковые системы используют Gradient Boosting Machine для автоматического анализа качества сайтов. Такой алгоритм строит большое количество decision tree, которые используют boosting (постепенное улучшение посредством повышения качества прогноза предыдущих decision tree). Перейдём к примеру. Вот несколько строк из файла входных данных:
0 1:86 2:33 3:79 4:77 5:74 6:81 7:90 8:63 9:8 10:27 11:33 12:29 13:99 14:14 15:92
1 1:100 2:82 3:18 4:8 5:73 6:27 7:18 8:11 9:25 10:46 11:79 12:88 13:62 14:12 15:20
0 1:98 2:53 3:79 4:74 5:26 6:60 7:64 8:89 9:67 10:91 11:22 12:95 13:90 14:35 15:87
0 1:89 2:17 3:4 4:96 5:89 6:31 7:13 8:99 9:55 10:59 11:78 12:43 13:20 14:90 15:62
0 1:20 2:88 3:14 4:99 5:62 6:40 7:58 8:26 9:28 10:25 11:16 12:49 13:20 14:5 15:84
0 1:6 2:94 3:100 4:10 5:89 6:88 7:40 8:2 9:87 10:95 11:61 12:65 13:37 14:81 15:55
1 1:99 2:100 3:42 4:12 5:98 6:4 7:52 8:56 9:29 10:79 11:80 12:44 13:28 14:99 15:49
0 1:5 2:42 3:11 4:14 5:31 6:98 7:54 8:33 9:85 10:48 11:93 12:49 13:85 14:73 15:3Предположим, что это некоторая статистика по самым важным поведенческим факторам. Первый символ строки — это класс (строго номинативная переменная: 0 или 1), а всё остальное — это характеристики объекта (индекс: значение). Этот набор данных необходим для машинного обучения. После этого модель сможет самостоятельно выявлять класс по вектору признаков. Существует второй такой же файл, но с другими наблюдениями. Он необходим для проверки правильности работы автоматической классификации.
Для обучения и проверки необходимо большое множество наблюдений, где уже точно известны классы (как вариант, можно прибегнуть к разделению выборки на учебную и проверочную части). Мы сравним фактический (уже известный) класс с результатом работы алгоритмов машинного обучения. В идеале, ROC-кривая точности работы бинарного классификатора должна иметь площадь под кривой, которая близка к единице. Но, если она близка к половине пространства, то это будет похоже на процесс случайного угадывания, что, естественно, категорически неприемлемо.
Предположим, что по условию задачи необходимо использовать дихотомическую (бинарную) классификацию. В данном примере количество деревьев будет 180 (с ограничением высоты до 4), а количество классов строго равно двум. У модели есть метод predict, который выполняет классификацию (возвращает метку класса) по указанному в качестве аргумента вектору:
import org.apache.spark.mllib.tree.GradientBoostedTrees
import org.apache.spark.mllib.tree.configuration.BoostingStrategy
import org.apache.spark.mllib.tree.model.GradientBoostedTreesModel
import org.apache.spark.mllib.util.MLUtils
/**
* Используем классификатор с указанными параметрами
*/
val boostingStrategy = BoostingStrategy.defaultParams("Classification")
boostingStrategy.numIterations = 180
boostingStrategy.treeStrategy.numClasses = 2
boostingStrategy.treeStrategy.maxDepth = 4
boostingStrategy.treeStrategy.categoricalFeaturesInfo = Map[Int, Int]()
/**
* Загрузка данных для обучения и для проверки
*/
val data = MLUtils.loadLibSVMFile(sc, trainingDataFile)
val newData = MLUtils.loadLibSVMFile(sc, testDataFile)
/**
* Обучение модели
*/
val model = GradientBoostedTrees.train(data, boostingStrategy)
/**
* Выявим точность модели
*/
val cardinality = newData.count
val errors = newData.map{p => (model.predict(p.features), p.label)}.filter(r => r._1 != r._2).count.toDouble
println(" Всего наблюдений = " + cardinality)
println(" Ошибок = " + errors)
println(" Точность = " + errors / cardinality)Такие алгоритмы можно использовать и в целях повышения конверсии сайтов. Подобный дихотомический (бинарный) классификатор очень удобен в практическом применении, так как требует только вектор признаков, а возвращает его класс. Можно в автоматическом режиме размечать огромные объёмы информации. Самым важным недостатком можно назвать необходимость наличия большого набора уже размеченных векторов признаков. Повторюсь, что очень многое будет зависеть от точности подбора признаков и от первичного анализа данных.
Машинное обучение и методы математической статистики применяются в самых разных областях науки и производства. Очень сложно провести грань между задачами оценки эффективности поведенческих факторов на порталах и задачами машинного обучения. Статистика применяется во всех сферах жизни человека. Более того, применение упомянутых алгоритмов машинного обучения позволяет выполнять такие задачи, которые ещё несколько лет назад были невозможными без участия человека.
5. Приложение
Код на R для визуализации показанных примеров.
#
# Загрузка данных
#
dataset <- read.csv("dataset.csv") # заранее сделан setwd(...)
#
# Линейная регрессия и кластерный анализ
#
plot(dataset, ylim=c(1, 25), xlim=c(1, 25), pch=20)
abline(lm(dataset$b ~ dataset$a), col = "blue")
clusters <- kmeans(dataset, 2, nstart = 50)
dimnames(clusters$centers) <- list(c("Alpha", "Beta"), c("X", "Y"))
points(clusters$centers, col="red", cex=1, pch=8)
text(clusters$centers, row.names(clusters$centers), cex=1.3, pos=4, col="red")
plot(hclust(dist(dataset, method="euclidean"), method="average"), col="blue")
#
# Отображение на графике и линейный коэффициент корреляции
#
title <- paste("Pearson's product-moment correlation: ", cor(dataset$a, dataset$b))
plot(dataset$a, type="o", main=title, lty=2, ylim=c(0, 25), xlim=c(0, 10), col = "red")
lines(dataset$b, type="o", pch=22, lty=2, col="blue")
#
# Библиотеки и загрузка данных
#
library(party)
library(randomForest)
library(gbm)
rd <- read.csv("rd.csv")
rd$class <- as.factor(rd$class)
#
# Дерево решений
#
plot(ctree(class ~ ., data = rd))
#
# Random Forest
#
varImpPlot(randomForest(class ~ ., data = rd, importance=TRUE,
keep.forest=FALSE, ntree=15), main="Random Forest")
#
# GBM
#
summary(gbm(class ~ alpha + beta + gamma + delta + epsilon + zeta,
data=rd, shrinkage=0.01, n.trees=100, cv.fold=10, interaction.depth=4,
distribution="gaussian"))
#
# Логистическая регрессия
#
summary(glm(formula = class ~ ., data = rd, family = binomial))