В поисках пути — царь Салтан осваивает лапласиан
… Молвит он: «Коль жив я буду, чудный остров навещу, у Гвидона погощу».

В царстве Салтана не без изьяна. Принят закон — не лезть за кордон, да тут князь Гвидон.
Опять прислал поклон, да приглашение на угощение,- надо принимать политическое решение.
Дворцовые интриганки, похожие на поганки, встали стеной — «мол, скажи, что больной». Но прослышал Салтан про Гвидонов кальян, про изумрудную белку, да богатырскую стрелку. А главная новинка — молодая жинка. В общем, ехать решено — «Я не был за морем давно».
Было однако одна проблема,- нужен был маршрут или схема. Поскольку никто (кроме Врангеля барона) не знал, как добраться до острова Гвидона. Корабельщики дали карту,- пришлось сесть за парту. Над картой склонился Салтан, — где тут остров Буян? Задача была как будто знакома — проложить путь к острову Гвидона. Но как найти дорогу, когда путей слишком много?
До ночи решал Салтан задачку, в итоге свалился в спячку. Снились ему матрицы и точки, да на болоте кочки. На кочку прыгнул Нео с острова Борнео.
— Если хочешь добраться ко сроку — плыви по максимальному потоку.
— Чего? — Салтан почти проснулся. Но Нео уже в зайца обернулся.
Карта и матрица смежности
Если вы не читали «Сказ царя Салтана о потенциале лапласиана», то, возможно, стоит это сделать сейчас. Мы используем приведенные там понятия.
Вектор потенциалов лапласиана соответствует стационарному (инвариантному) вектору состояний в теории марковских цепей.
Упростим задачу Салтана,- рассмотрим лишь 7 островов. На карте приведены возможные пути между островами и их длина — в днях.
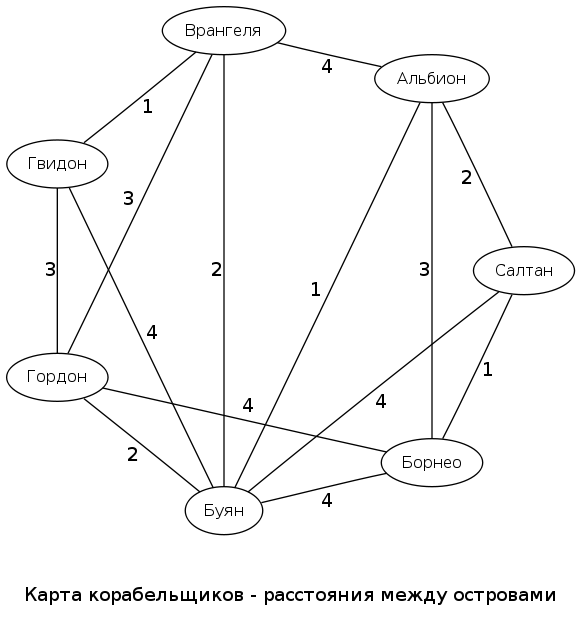
Да, карта выглядит несколько кривовато, но не будем слишком строги к корабельщикам. Найти оптимальный (самый короткий) путь от Салтана до Гвидона для данной карты несложно. Вот он:»(S)алтан > (А)льбион > (Б)уян > (В)рангеля > (G)видон». Итого 6 дней пути.
Нас интересует общий способ решения подобных задач — тогда мы сможем искать пути для графов произвольных размеров. Есть разнообразные алгоритмы перебора, но это не для нас. Мы владеем потенциалом лапласиана и хотим использовать этот потенциал.
Первый шаг очевиден. Надо от матрицы расстояний перейти к матрице смежности (связности). Чем больше расстояние между островами — тем менее они связаны. То есть величина связи обратно пропорциональна расстояниям. (В электронике аналогично — проводимость обратно пропорциональна длине проводника).
Тогда матрица смежности островов принимает следующий вид (значения округлены, 0.33 = ⅓):
Данная матрица (в отличие от рассматриваемых в предыдущей статье) является симметричной, то есть граф связности неориентированный.
Задача поиска пути разбивается на две. Первая — это найти хоть какой-то путь между заданными точками, методику гарантированного достижения цели из заданного источника. Вторая — из множества путей выбрать оптимальный. В данной статье мы рассмотрим первую, относительно простую.
Для решения данной задачи нам необходим некий критерий, который бы позволил ранжировать острова в зависимости от расстояния до цели. Тогда при выборе острова, на который можно доплыть из заданного, мы будем знать, приближаемся мы к цели или нет.
Потенциалы островов
Таким критерием могут служить значения потенциалов каждого острова. Да-да, тот потенциал 1-го порядка, который мы использовали в предыдущей статье. Однако мы не можем напрямую использовать потенциал лапласиана. Для симметричных матриц (ненаправленных графов) все значения такого потенциала равны между собой и называются постоянной матрицы Кирхгофа. В симметричных лапласианах данная постоянная играет роль детерминанта (определителя). Будем далее называть постоянную Кирхгофа общим (скалярным) потенциалом — просто термин (может, и не особо удачный).
Итак, в симметричных лапласианах вектор потенциалов становится скаляром — общим потенциалом. Для нашего лапласиана значение общего потенциала равно примерно 8.61. Считается просто — на основании матрицы смежности строится лапласиан (как — рассказано ранее), удаляем из лапласиана любую строку и столбец и считаем определитель. Это и есть наш общий потенциал.
Все это здорово, но для поиска пути пока бесполезно. Нам-то надо, чтобы потенциалы островов были разными, и при этом изменялись от максимального (Салтан) до минимального (Гвидон) или наоборот, без разницы. Как этого добиться?
Есть два красивых способа (а может, и больше). Первый — классический. Поэтому начнем с него.
1-й Способ. Решаем задачу Дирихле
А классика состоит в том, чтобы использовать аналогию электрических (ну и марковских тоже) цепей. Раз нам нужные разные потенциалы, значит, надо просто приложить разность потенциалов между исходным состоянием (островом) и целевым. Данная разность приведет к тому, что между узлами (островами) потечет поток и, как следствие, у каждого острова появится свой потенциал.
Здесь важно то, что значения потенциалов являются гармоническими, то есть значение каждого потенциала является средним относительно значений соседних потенциалов. У таких гармонических векторов (функций) есть одно свойство — минимальное и максимальное значение они принимают на границе. В нашем случае границами являются узлы, в которых задано (фиксировано) значение потенциала, то есть острова Салтана и Гвидона. Гармоничность вектора потенциалов гарантирует нам то, что на одном из данных островов потенциал будет максимальным, а на другом — минимальным. А потенциалы остальных островов будут находиться где-то между ними. Что нам и нужно.
Если мы присваиваем острову Гвидона меньший потенциал, то при поиске пути от Салтана нам нужно выбирать только те острова, потенциал которых меньше текущего и исключать острова с большим потенциалом.
Осталась малость — найти значения потенциалов островов. Данная задача похожа на ту, что мы решали в 1-й статье, поэтому мы снова приведем уравнение баланса в форме, подчеркивающей гармоничность потенциалов U:
Отличие в том, что сейчас у нас часть потенциалов задана. Принято называть такие значения граничными. Термин, может, и не очень удачный, но общепринятый.
Задачу нахождения неизвестных потенциалов по известным на границе обычно называют задачей Дирихле. У нее есть решение (что радует).
Фундаментальная матрица
Отметим, что величина связей (проводимости) между узлами, потенциалы которых заданы, не имеют значения. То есть они (эти связи) не влияют на решение. Поэтому из лапласиана можно исключить заданные (граничные) узлы. В нашем случае из лапласиана исключаем острова Салтана и Гвидона. Получаем дополнительный минор лапласиана, вот такой:
Обратная матрица данного минора называется фундаментальной (термин из теории марковских цепей с ловушками). Для нашей карты фундаментальная матрица имеет вид (сверяйтесь):
Далее нам нужна связь внешних узлов (у нас это острова Салтан и Гвидон) с внутренними. То есть минор матрицы смежности, в котором оставлены только две колонки:
Умножая фундаментальную матрицу на данный минор связи внешнего и внутреннего (миров) мы получаем матрицу влияния внешнего на внутреннее (и близки к завершению маневра). Вот наша матрица влияния:
Значения элементов данной матрицы отражают вклад внешнего потенциала во внутренний. Например, вклад потенциала острова Салтана в потенциал острова Буяна составляет 0.513. Задавая теперь внешние потенциалы (Салтана и Гвидона), мы можем рассчитать потенциалы всех остальных островов простым умножением матрицы влияния на вектор внешних потенциалов. По моему, очень круто.
Сумма значений по каждой строке равна 1, то есть веса вкладов нормированы. Это означает, что чем ближе остров к Салтану, например, тем дальше он от Гвидона, ну и наоборот.
Для решения нашей задачи ранжирования островов в принципе достаточно данной матрицы, поскольку на основе ее значений мы уже можем сортировать острова по дальности/близости от цели. То есть до цели мы добраться сможем, но сначала рассмотрим
еще один способ расчета потенциалов островов.
2-й Способ. Возмущение симметричного лапласиана
Ранжирование потенциалов островов через фундаментальную матрицу — это универсальный подход. Как и все универсальное он является немного избыточным (тяжеловесным) для нашей задачи. Можно поступить проще, а именно — возмутить матрицу Кирхгофа (лапласиан островов).
Как отмечено выше, для симметричного лапласиана все компоненты вектора потенциалов равны. Нам же нужно, чтоб они были неравны. Соответственно, надо сделать лапласиан несимметричным. Как это сделать — тоже понятно. Поскольку нам нужен градиент потенциалов от острова Салтана до Гвидона, то и возмутить нам надо соответствующую связь. Эта связь задаст градиент потенциалов.
Что такое «возмутить связь»? Это означает, что в матрице смежности (проводимости) значение связи в одном из направлений мы увеличиваем на некую дельту (например, на 1). При этом в обратном направлении значение не меняем. Например, задаем, что остров Гвидона связан с островом Салтана, но в обратном направлении связи нет.
В каком-то смысле такое искажение (возмущение) матрицы смежности (и лапласиана) эквивалентно приложению внешнего потенциала к островам. Ведь для поддержания разности внешних потенциалов между узлами нужна какая-то связь (в электронике — батарея).
Для возмущенной матрицы мы можем уже посчитать потенциалы островов как потенциалы 1-го порядка, введенные в предыдущей статье.
Наш возмущенный разум лапласиан островов имеет вид:
Отличие от невозмущенного — единица в правом верхнем углу, которая и является «возмущением». Вектор потенциалов такой матрицы равен (способ расчета в предыдущей статье):
Возникает вопрос, а будут ли эквивалентны вектор потенциалов возмущенной матрицы и вектор потенциалов, рассчитанный через фундаментальную матрицу? Если кратко, то да. Проще всего в этом убедиться, подставив в качестве заданных внешних потенциалов возмущенные потенциалы островов Салтана и Гвидона (25.28, 8.61). Умножая данный вектор из двух значений на матрицу влияния, мы получаем внутренние значения потенциалов.
Почему так получилось? Попробуем разобраться. Во-первых, наши возмущенные потенциалы тоже являются гармоническими, так как удовлетворяют такому же уравнению баланса. Во-вторых, краевые значения возмущенного потенциала тоже всегда экстремальны — одно из них (в нашем случае это потенциал Салтана) — максимально, а другое (потенциал Гвидона) — минимально (если поменять направление возмущения, то соответственно будет наоборот). Чтобы понять, почему возмущенные потенциалы экстремальны, нам надо выяснить — как они считаются/получаются.
Производные потенциала
Допустим, нам надо ранжировать острова в другом порядке — не от Салтана до Гвидона, а, к примеру, от Гордона до Альбиона. Каждый раз считать при изменении задающих направление островов детерминанты и/или обратные матрицы не выглядит хорошей идеей. Нельзя ли один раз что-то обратное посчитать, а потом просто использовать это обратное?
Посмотрим, как изменяется общий (скалярный) потенциал при возмущении. На языке формул это означает, что нам надо найти производную (изменение) общего потенциала при изменении значения какой-либо связи. Удача в том, что как указывалось ранее — любой потенциал определяется суммой произведений связностей. То есть все условно-линейно и производные должны быть несложными.
Зависимость потенциала первого порядка от значения связности
определяется потенциалами 2-го порядка:
Что понимается под «порядком потенциала»? Для получения потенциала 1-го порядка надо удалить из лапласиана по одной строке и столбцу. Для получения потенциала 2-го порядка, надо удалить две строки и два столбца. Для 3-го — удаляем по три и т.д. У оставшейся после удаления строк и столбцов матрицы (которая называется дополнительным минором) считаем определитель — его значение и будет соответствующим значением потенциала n-го порядка. Ну и поскольку мы начали использовать потенциалы 1-го и 2-го порядков, то удобно первые называть векторным потенциалом, а вторые — матричным.
В формуле (2.1) потенциалом 2-го порядка является . Индексы разделены запятыми,- первые означают удаляемые строки, 2-е — столбцы (возможно, наоборот).
Присвоим нашим возмущаемым островам индексы. S — Салтан, G — Гвидон, а острову Буяну индекс B. Тогда изменение потенциала острова Буяна при возмущении связи «G — S» можно выразить как
Посчитаем данное изменение для нашего лапласиана. Удалим из лапласиана соответствующие строки и столбцы и рассчитаем определитель. Получим, что . Это же значение получается, если вычесть из потенциала острова Буяна потенциал острова Гвидона (который совпадает с общим невозмущенными потенциалом): 17.15 — 8.61 = 8.55. То есть все верно, формула работает (это потому что мы выбрали единичное возмущение — в общем случае надо не забывать еще умножать на изменение связности C).
А что будет, если мы посчитаем по формуле (2.1) потенциал возмущаемых островов — Салтана и Гвидона? Подставляя соответствующие индексы в формулу (2.1'), получаем:
Переводя на русский язык, — потенциал острова Гвидона при возмущении SG не меняется (остается равным общему), а потенциал острова Салтана изменяется на величину главного потенциала 2-го порядка.
Виды потенциалов
Сделаем небольшое отступление, чтобы рассказать про «главные» и другие виды потенциалов. Мы называем потенциалы главными, если удаляемые из лапласиана индексы строк совпадают с индексами колонок. Поэтому для главных потенциалов достаточно указывать только один набор индексов, то есть .
А какие неглавные виды бывают? Еще две ситуации возможны, — удаляемый набор индексов строк пересекается с индексами колонок (назовем такие потенциалы смежными) и не пересекается (свободные потенциалы). В формуле (2.1) задействован смежный потенциал (пересечение по индексу k).
Теперь, внимание! Подарок богов состоит в том, что все неглавные потенциалы можно выразить через главные. Вот общая формула для симметричных лапласианов:
,
из которой следует выражение для смежных потенциалов:
Подставляя (2.4) в (2.1), получаем связь производной потенциалов узлов с главными потенциалами:
Та дам! Это формула и есть инструмент, который мы искали. Осталось его осмотреть, завести и можно пользоваться.
Матрица потенциалов 2-го порядка
Итак, по-настоящему фундаментальной матрицей для симметричных лапласианов (неориентированных графов) является матрица главных потенциалов 2-го порядка. Приведем ее вид для наших островов:
Рассчитаем по данной матрице приращение потенциала острова Буяна при возмущении связи Салтана с Гвидоном:
Эту цифру мы уже видели раньше, так что похоже, что формула работает.
Как получить данную матрицу по заданному лапласиану? Можно, конечно, тупо удалять строки/столбцы и считать определители миноров, но это затратно и неэффективно. Поэтому обычно поступают по-другому. Возьмем дополнительный минор лапласиана (то есть удалим любую, например 1-ю, строку и колонку) и рассчитаем для него присоединенную матрицу (присоединенная — это обратная, значения которой умножены на определитель). Полученная таким образом матрица является свернутым потенциалом, но его можно развернуть, применив к значениям преобразование дистанции (да, много непонятных терминов, но как-то же надо все это называть). В итоге получим искомые матричные потенциалы. То есть вот такая схема Горнера:
Матрица потенциалов = Дистанция (Присоединенная матрица (Доп. минор (Лапласиан)))
Преобразование дистанции выглядит следующим образом:
для симметричных матриц
Матрица потенциалов напрямую связана с матрицей резистивных расстояний (значения отличаются на множитель общего потенциала), а также с матрицей Грина, которая является обратным лапласианом, но обо всем этом как-нибудь в другой раз.
Связь с геометрией
Значения матричного потенциала пропорциональны квадратам расстояний между узлами графа. В самом деле, если мы приглядимся к значениям матрицы и сопоставим их с картой корабельщиков, то увидим, что данное утверждение похоже на правду — наибольшее значение (16.67) между островами Салтана и Гвидона.
Это наводит на мысль о том, что производной векторного потенциала можно придать геометрический смысл. Запишем формулу (2.5) в виде
(здесь мы использовали обозначения
), и сравним данную формулу с известной из школьного курса теоремой косинусов
Тогда получаем следующую связь между производной векторного потенциала и параметрами треугольника (индексы привели к обозначениям вершин треугольника i=C, j=B, k=A):
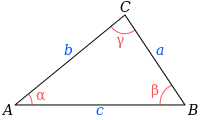
Формула (2.6) описывает изменение потенциала вершины C при изменении проводимости (связности) противоположной стороны треугольника — BA. Обратим внимание на то, что формула несимметрична относительно перестановки BA. Это связано с тем, что производная потенциала зависит от направления:
Если изменить направление, то значение производной будет выражаться через другие стороны и другой угол:
Формула (2.7) демонстрирует экстремальность потенциалов возмущаемой стороны треугольника. Поскольку значения косинуса угла всегда (по модулю) меньше 1, то очевидно, что экстремальные значения потенциалов треугольника будут только при совпадении вершины C с одной из других вершин треугольника (A или B). Такая вот неожиданная связь свойств гармонических функций со свойствами треугольника.
Резюме
Нам пора закругляться. Бросим еще раз взгляд на то, что мы рассмотрели. Мы искали способ нахождения путей в графе, который свелся к методам ранжирования узлов неориентированного графа.
Пусть нам дан набор связанных между собой объектов (связь может отражать, например, степень близости объектов). Мы не можем отсортировать данные объекты если у нас нет критерия сортировки,- все объекты одинаковы. Но если мы теперь выберем некие два объекта из набора и укажем, что один из них самый большой, а другой — самый маленький, то все остальные объекты поддаются ранжированию по их степени близости к большому или маленькому. Простым заданием границ (большой и маленький объекты) мы поляризуем остальные объекты (наделяем их разными потенциалами) по отношению к заданным границам.
Занятно.
Ну и да, отплывать еще рановато. Мы нашли способ гарантированного доплытия до пункта назначения, но не указали, как найти оптимальный (самый короткий) путь. Не переключайтесь).
