Усы и наждачка: динамика вибрисс при контакте с поверхностью
Оглянитесь вокруг. Что вас окружает? Какие бы ответы не последовали, их можно объединить одним словом — информация. Звуки, запахи, цвета, текстура предметов и даже температура помещения это совокупность данных об окружающей среде, которые безустанно собирают наши органы чувств. Каждый из них важен для получения общей картины мира, который нас окружает. Одним из самых загадочных чувств является осязание, т.е. тактильное восприятие давления, вибрации, текстуры объекта или температуры. За это отвечает наша кожа, а точнее многочисленные рецепторы в верхних слоях дермы. Но вот у многих животных эти функции выполняют вибриссы, т.е. усы. Если у вас есть кот, то вы наверняка знаете насколько чувствительны усы этого млекопитающего. Малейшее дуновение ветра или прикосновение вызывает ответную реакцию. Ученые из Бристольского университета (Англия) решили рассмотреть, как именно работают вибриссы на примере крыс. Каковы механические свойства вибрисс, насколько они чувствительны, какие процессы протекают в момент их активации, и как полученные данные можно спроектировать на человека? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.
Основа исследования
Когда ученые изучают зрение, они рассматривают не только глаза, нервы и мозг, но и сами изображения, которые мы видим. Другими словами, при изучении восприятия важно учитывать специфичные физические и химические свойства объектов сенсорики, а также их взаимодействие с самими сенсорами.
В случае с тактильными системами, выделяют трение, возникающее при движущемся механическом контакте сенсора (волос и кожи) и предмета, с которым он соприкасается. С точки зрения сенсорики трение это короткие и резкие движения («прилипание/скольжение» или просто «проскальзывание»), которые возникают из-за накопления и высвобождения энергии при деформациях упругих объектов на микроскопическом уровне.
Для человека основным инструментом восприятия трения является кожа. Но у грызунов, как и у многих других млекопитающих, эту функцию выполняют еще и вибриссы, т.е. усы, расположенные на морде. Вы могли неоднократно замечать, как коты, обнюхивают какой-то предмет. Но для получения обонятельной информации нет необходимости находиться близко к объекту, учитывая острый нюх котов. Во время этого действа, кот прикасается своими вибриссами к объекту, дабы собрать тактильную информацию в дополнение к обонятельной. Стоит отметить, что зрение котов не самое лучшее на малых расстояния, потому вибриссы заполняют пробелы, образованные в визуальной информации, если интересующий объект слишком близко.
Как работают вибриссы котов.
У грызунов вибриссы имеют конусообразную форму, что придает им необычайную эластичность. Подвижность вибрисс также удивительно, а потому животное может «настраивать» их положение в зависимости от сложившейся ситуации.
Наблюдения за взаимодействием крыс и текстурированных объектов показали, что последовательности событий «прилипания/скольжения» позволяют получать значительный объем текстурной информации, а также информации о контексте, например скорость и расстояние до поверхности текстуры. Также было установлено повышение нейронной активности в дерме, во время контактов вибрисс и объекта.
Изучение биомеханических свойств вибрисс позволило ученым предположить, что решающими факторами стимуляции механорецепторов в фолликуле являются динамические переменные — сила и момент.
Проблема изучения вибрисс заключается в их кинематике. Посему ученые считают, что для понимания работы вибрисс важно выяснить, как кинематические переменные, относящиеся к кончикам усов, связаны с динамическими переменными. Кроме того, остается загадкой принцип механической передачи сигналов по усу от очень гибкого кончика к гораздо более жесткому фолликулу, где генерируются нейронные сигналы. Подходящим для этой задачи инструментом ученые называют математическое моделирование.
На данный момент механику усов изучают либо с помощью линейной теории пучков, либо с помощью квазистатического приближения эластики Эйлера* с неоднородными осевыми свойствами.
Эластика Эйлера* — искривленная форма, которую принимает стержень в момент потери устойчивости (прямолинейной формы равновесия).
Данные методики позволяют определить частоты линейных колебаний вибрисс и квазистатические нелинейные деформации, такие как коробление, возникающие когда гибкий кончик уса находится в постоянном контакте с поверхностью. Однако эти методики не позволяют оценить динамические силы в момент передачи волн проскальзывая от кончика вибриссы до фолликула.
В данном же труде ученые решили адаптировать модель эластики Эйлера, включив в нее быструю динамическую деформацию, когда усы находятся в контакте с поверхностью. Модель стержневой механики Коссера (книга братьев Коссера «Theory of Deformable Bodies» / переведено на английский) была использована для моделирования динамики, скорости, силы и момента в каждой точке вдоль центральной оси уса.
Результаты исследования
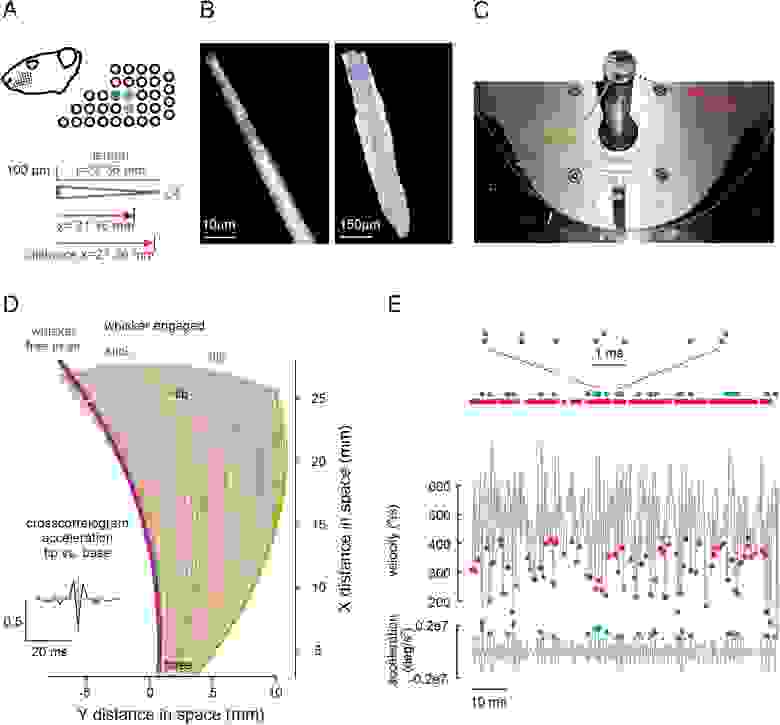
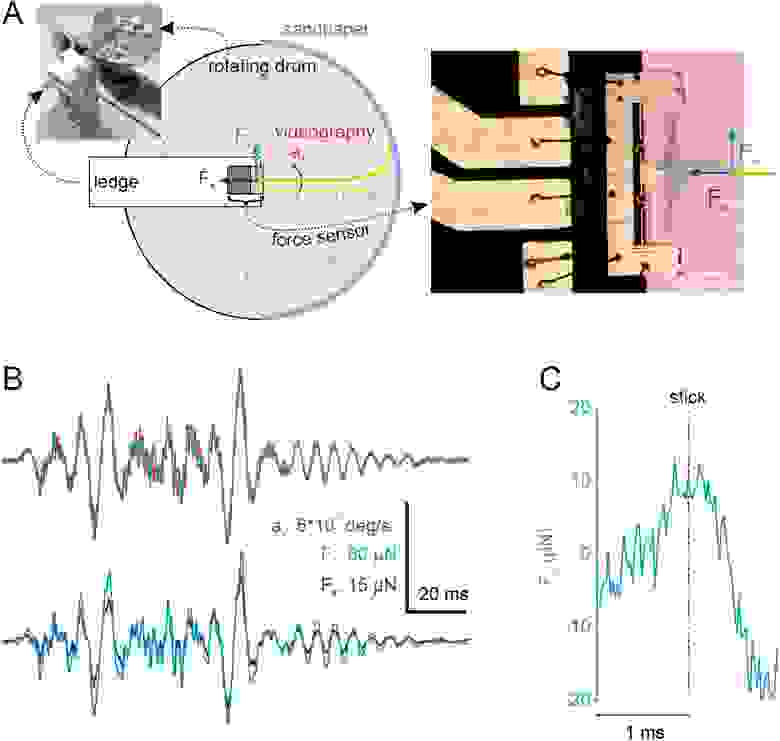
Изображение №1
В ходе наблюдений использовался ус (1A и 1B), фолликулярный конец которого был прикреплен к вертикальному валу, который вращался с постоянной угловой скоростью с помощью шагового двигателя (1C). Ус вращался и кончиком контактировал с внутренней частью вертикально установленной полуцилиндрической камеры, покрытой наждачной бумагой разной шероховатости. Центр камеры совпадал с точкой крепления уса.
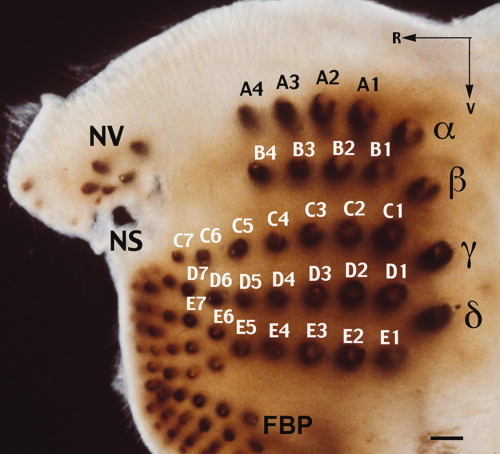
Положение усов крысы и соответствующие им обозначения.
В исследовании использовался ус C4, длина (l) которого составляла 28.36 мм, а радиус у основания — 69 мкм. Результаты наблюдений впоследствии были подтверждены опытами с усами C3 и D3. Форма вибриссы была конусной за исключением самого кончика, где в области с радиусом 3 мкм наблюдалось усечение.
Скорость вращения вала составляла 420 об/с (в некоторых опытах 840 об/с и 1260 об/с). Расстояние до объекта касания было либо x = l − 1 мм, либо x = l − 7 мм (т.е. длина уса минус 1 или 7 мм). Были приняты меры, чтобы выровнять внутреннюю кривизну усов с горизонтальной плоскостью и измерить только движение к вогнутой стороне усов. На морде крысы такое движение в значительной степени соответствовало бы вытягиванию усов вперед.
Движение свободного стержня усов (т.е. участка от кончика, контактирующего с наждачкой, до участка, зафиксированного клеем к валу) отслеживалось с помощью камеры с высокой частотой кадров (4 кГц; 1C).
В ходе анализа полученных снимков и записей оценивалась нормальная скорость (в плоскости вращения, соприкасаемой с усом) и ускорение в каждой точке вала.
Кинематические следы точки в 3 мм от основания использовались для определения «фаз прилипания» как интервалов, когда нормальная скорость становилась ниже скорости вращения шагового двигателя. Также отслуживались «фазы скольжения» как интервалы, в которых ускорение усов превышало значение двух стандартных отклонений распределения ускорения при бесконтактном движении (без контакта с наждачной бумагой). Визуализация положений усов в соответствии с фазами прилипания и скольжения показывает заметные и чередующиеся события прилипания/скольжения при трении (1D).
Сведение к минимуму скорости в фазах прилипания и максимизация ускорения в фазах скольжения привело к появлению явных событий прилипания и скольжения (зеленые и красные точки на 1E). События скольжения четко различимы по следам ускорения как на вершине, так и на основании усов. При этом их внешний вид менялся в зависимости от типа наждачной бумаги (P80 — размер зерна 200–250 мкм или P1200 — размер зерна 10–14 мкм) или в зависимости от расстояния до контактной поверхности.
Чтобы выяснить скорость биомеханической передачи от кончика к основанию уса, был построен график ускорения кончика и основания в плоскости движения усов (кончик: ax(s = 24 мм); основание: ax(s = 3 мм)) и рассчитана их взаимная корреляция. Было обнаружено, что ускорение в этих двух точках имеет отрицательную корреляцию, т.е. когда наконечник ускоряется, основание замедляется (вставка на 1D).
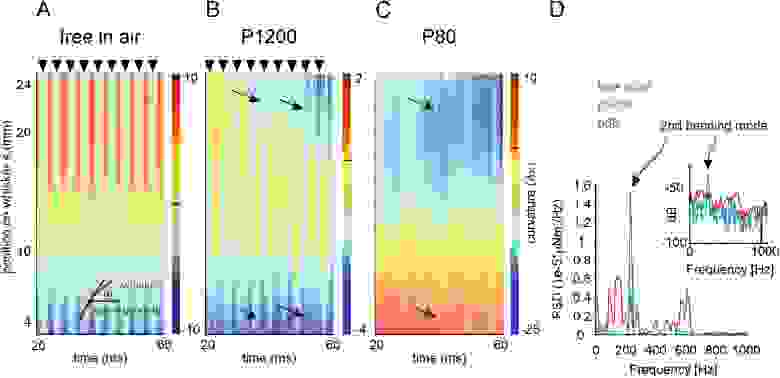
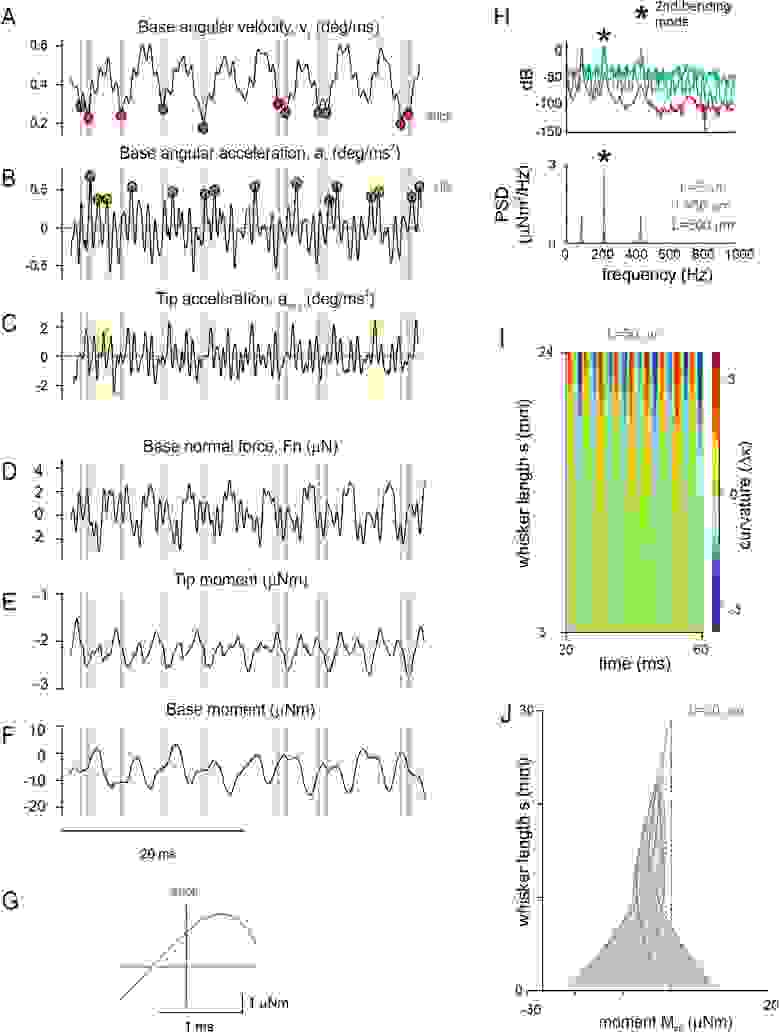
Изображение №2
Далее необходимо было выяснить, как наблюдаемые противоположные направления движения около кончика и основания уса проявляются вдоль всей его длины. Для этого была оценена локальная кривизна (во всех пикселях на центральной линии уса) путем определения угла θ, охватываемого вектором, ортогональным к основанию усов, а также касательной силы, действующей на луч уса (вставка на 2А). Кривизна (κ) определяется пространственной производной θ, т.е. κ(s) = dθ/ds.
На график была нанесена кривизна κ = κi — κ (т.е. кривизна относительно внутренней кривизны (κi) уса во всех точках вдоль вала в каждый выбранный момент времени во время одного опытного захода (2A-2C).
При движении в воздухе (т.е. без контакта с бумагой) колебания уса приводили к изменению его формы от изначальной (κ = 0) до отклонения с загнутым назад кончиком (κ (tip) > 0) и отклонения с основанием, изогнутым вперед (κ (base) < 0). Частота колебаний была близка к 200 Гц (2А).
Когда ус контактирует с более гладкой наждачной бумагой (размер зерна P1200; на расстоянии x = l − 1 мм), κ на кончике изменяется на прямое направление κ (tip) < 0 (2B и 2C). Таким образом, свободные колебания уса затухали, тем не менее были видны примерно с той же частотой. Кроме того, стали видны быстрые волны, соответствующие началу скольжения. Они выглядят как неправильные вертикальные полосы. Вертикальный характер этих полос снова предполагает их сверхбыстрое прохождение вдоль луча. Аналогичные результаты наблюдались с Р80, т.е. с более грубой наждачной бумагой (2С).
При движении в воздухе и при использовании бумаги P1200 наблюдалась стабильная вторая гармоника колебаний (2D). Данная колебательная схема нарушается, когда ус находится в контакте с грубой наждачной бумагой P80, так как в сигнатуре начинает преобладать сигнал событий прилипания и скольжения.
Измерения кривизны позволили определить момент Mna (s, t) (охватываемый нормальной силой (Fn) и осевой силой (Fa); вставка на 3B) вокруг вертикальной оси в каждой точке вдоль центральной линии уса (s) и в любой момент времени (t). Эффект Mna заключается в локальном изгибе луча вибриссы в рассматриваемой точке в плоскости ее движения.
Для каждой точки положения (s) Mna можно рассчитать с помощью модуля Юнга (E) луча, его кривизны k (s), собственной кривизны уса κi (s) (3A) и вторичного момента.
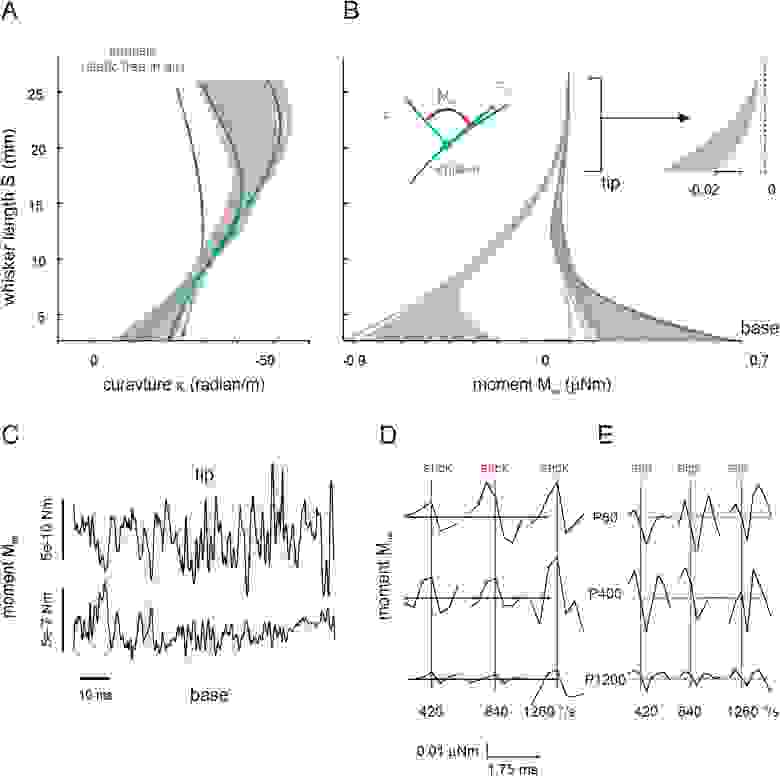
Изображение №3
Учитывая, что ус сильно заострен на конце, по мере приближения к основанию происходит непрерывное наращивание силы момента вдоль уса. Следовательно, крошечные силы, отклоняющие дистальную гибкую часть уса, приводят к нарастанию момента вдоль всего его луча. Этот процесс обеспечивает передачу в основание уса стабильного и сильного моментного сигнала в ответ на малейшие отклонения кончика уса (3B).
Чтобы количественно оценить усиление момента, было рассчитано отношение дисперсии моментов, измеренных на кончике (на расстоянии 1 мм от вершины) и на основании (также на расстоянии 1 мм от конца основания). Это отношение составляло 1.4e-4 для уса C4 (3B).
Дополнительно были измерены отношения и для усов типа С3 и D3 (изображение №4). Но в их случае вращалась сама камера с наждачной бумагой, а не ус, как в случае с C4. Такие тесты показали еще меньшее отношение, т.е. более высокое усиление (C3, длина 44.56 мм, отношение — 2.6e-4; D3, длина 45.22 мм, отношение — 2.57e-4).
Любопытно, что внутренняя кривизна (κi) сдвигает диапазон моментов, испытываемых фолликулом, так что в результате происходит изменение знака. Вполне вероятно, что именно этот эффект играет ключевую роль в том, что ус вибрирует в основном во втором режиме изгиба.
Первый и второй режимы изгиба на примере I-образной балки (подробнее о режимах изгиба можно узнать из видео).
На 3C показан временной ряд Mna на вершине и в основании, а также их обратное соотношение. Анализ момента в основании в фазах прилипания и скольжения выявил систематическую взаимосвязь между двумя переменными: в среднем момент накапливается во время фазы прилипания (3D) и высвобождается во время скольжения (3E).
Из вышеописанных данных следует, что конусная форма уса вместе с его внутренней кривизной играют важную роль в определении диапазона моментов, испытываемых в фолликуле.
Изображение №4
Дабы проверить расчеты момента из данных кинематики, было решено измерить силу, действующую на основание уса при контакте с наждачной бумагой. Для этого использовался пьезорезистивный датчик силы, способный измерить многоосные силы в диапазоне от нано- до микроньютонов (4A).
Ус был зафиксирован в одном положении, а бумага покрывала вращающийся барабан. В этой конфигурации датчик мог измерять нормальную (Fn) и осевую силу (Fa), действующую на основание уса (светло-синие и темно-синие стрелки на 4A). Дополнительно использовалась скоростная съемка с частотой кадров 9.6 кГц, чтобы измерить ускорение (ax) вблизи основания.
Было установлено, что Fn, Fa и ax сильно коррелированы: |rFn, ax| = 0.9349; |rFa, ax| = 0.9302; |rFn, Fa| = 0.9657 (4B). Как следствие, средняя сила, наблюдаемая во время фаз прилипания, показывает четкий пик (4C).
Из этого следует, что временной ряд ускорения, измеренного около основания, сопоставим с таковым для сил, действующих в этой же области уса. Однако, как уточняют сами ученые, использовать ускорение в качестве «заменителя» в измерении силы это крайне неточный метод. Проблема в том, что момент (а может и силы тоже) очень сильно увеличивается от вершины до основания, а ускорение — нет.
В заключение было проведено моделирование процесса контакта вибриссы с наждачной бумагой на основе механики Коссера.
Ус в моделировании был представлен как усеченный конус с длиной l (от основания до точки усечения) и однородными линейно-упругими свойствами материала (т.е. с постоянным модулем Юнга). Стоит отметить, что эластичность стержня для изгибающего движения перпендикулярно его продольной оси будет значительно увеличиваться от основания к вершине, поскольку круговое поперечное сечение уменьшается. Как и в практических опытах, в моделировании стержень двигался в горизонтальной плоскости, образованной внутренней кривизной (с вершиной, изогнутой в направлении движения наждачной бумаги).
Авторы исследования отмечают, что точное моделирование эффектов высокоскоростного динамического трения между двумя сухими поверхностями является крайне сложной задачей. В научном мире нет общепринятой методики, которую можно применять для решения этой задачи. Посему было решено поэкспериментировать и использовать так называемый закон трения по скорости и состоянию.
Этот подход моделирует динамический коэффициент трения (μ) и результирующую силу трения (FT = μp) на основе параметров прошлой истории скольжения (состояние контакта) и относительной скорости между взаимодействующими поверхностями (скорость деформации). Эта формулировка богаче, чем классическое кулоновское трение, поскольку она дополнительно позволяет установить параметр L, называемый «длиной скольжения», который иногда считается показателем шероховатости.
Изображение №5
Анализ кинематической картины модели в установленном режиме (при L =10 мкм, v = 0.2 м/с (т.е. 420 об/с) и α = 1) показал, что модель успешно генерировала фазы и события скольжения и прилипания.
Базовая угловая скорость (5A) регулярно занижает скорость движения, и за ней следуют переходные процессы, превышающие ускорения, наблюдаемые без контакта. Поиск локальных экстремумов выявил картину прерывистого скольжения, аналогичную той, что наблюдалась в экспериментах (5A и 5B). Моделирование также показало, что ус вибрировал во втором режиме изгиба, как это было видно и в ходе практических опытов (5B и 5C). Также было подтверждено наличие сильной корреляции между кинематическими и динамическими переменными: ускорение и нормальная сила коррелировали с коэффициентом r = 0.44. Этот показатель ниже, чем на практике. Это отображает тот факт, что в модели ус контактирует с гладкой поверхностью, тогда как на практике с наждачной бумагой.
Моменты вершины и основания возникали в противоположных направлениях, отражая второй режим изгиба (5D, 5E и 5F). Построение графика среднего момента вокруг событий прилипания (5G) показало, что за событием прилипания следует увеличение момента вдоль всего уса. Следовательно, как и было показано на практике, во время прилипания момент накапливается, а затем высвобождается во время скольжения.
Дабы определить идеальное значение L, модель была запущена с разным значением L (от 5 до 500 мкм). Полученные в результате спектры положения (5H) показали, что преобладание второго режима изгиба, наблюдаемого в экспериментах, лучше всего представлено средними значениями L (т.е. около 50 мкм).
Зная подходящее значение L, был построен график кривизны (κ), показывающий колебания аналогичные тем, что наблюдались на практике (5I). Расчет моментов вдоль луча уса показал сильное увеличение от вершины к основанию с узлом изгиба, расположенным в нижней половине уса (5J), что также соответствовало практическим данным.
Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.
Эпилог
В данном труде ученым удалось с помощью практических опытов и математического моделирования получить уникальные данные о том, как вибрации передаются от кончика к основанию уса при контакте с текстурированной поверхностью.
Ученые выяснили, что передача вибраций от кончика уса к основанию является сверхбыстрой и реализует второй режим изгиба. Когда вершина уса начинает колебаться, образованное движение в виде момента передается на основание. Из-за сужения, вызванного конусообразной формой уса, еле заметный момент на кончике, проходя по оси уса, многократно увеличивается.
Это наблюдение показывает, что морфология усов крыс (как и других млекопитающих) невероятно сложна и обладает сверхточной настройкой, если можно так выразиться. Однако полученные сведения не ограничиваются лишь грызунами и котами. Их можно применить и для изучения того, как человек, прикасаясь к чему-то, ощущает текстуру поверхности. Конечно, морфология кончиков пальцев человека гораздо сложнее усов крысы, но принципы, лежащие в основе их сенсорной работы, могут быть очень схожи.
Ученые считают, что их находки могут найти свое применение во многих отраслях, от медицины и протезирования до робототехники. Зная, как именно мы ощущаем поверхности на ощупь, можно менять их характеристики, тем самым, к примеру, создавая более ощутимые текстуры для слабовидящих или незрячих людей. Кроме того, более глубокое понимание этого вопроса может стать основой для создания сверхчувствительных протезов или даже роботов, способных ощутить малейшие элементы текстуры на любой поверхности даже в условиях плохой видимости.
И такие варианты практического применения делают это исследование еще более удивительным, учитывая, что все началось с уса обычной крысы.
Отношение к крысам у каждого свое. Кто-то их терпеть не может, кто-то держит дома в качестве питомца, а кто-то строит для них храм.
Благодарю за внимание, оставайтесь любопытствующими и отличных всем выходных, ребята! :)
Немного рекламы
Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5–2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).
Dell R730xd в 2 раза дешевле в дата-центре Maincubes Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5–2697v3 2.6GHz 14C 64GB DDR4 4×960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5–2430 2.2Ghz 6C 128GB DDR3 2×960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5–2650 v4 стоимостью 9000 евро за копейки?

