Умный в гору не пойдет
Доброго дня, хабровчане!
Поделюсь с Вами одним численным алгоритмом вычислительной математики для построения оптимального пути движения на сложной поверхности. Под оптимальностью понимается построение такого маршрута, который проходит по карте местности, огибая все локальные экстремумы (возвышенности и впадины), обеспечивая таким образом некоторую степень минимизации перепада высот и длину всего маршрута.
Входная поверхность задана множеством точек (облаком точек) в трехмерном евклидовом пространстве и имитирует собой ландшафт со всеми его неровностями: возвышенности, холмы, горы, овраги, впадины, разломы и т.д. В качестве начального условия выбирается любая точка на поверхности.
Задачу можно рассматривать как продолжение уже имеющегося маршрута. Куда в конце концов упрется наш искомый путь нам неважно, — главное начать, а там как пойдет, чтобы он обогнул неровности. Алгоритм также не гарантирует прохождения маршрута через какие-либо заранее заданные точки из входного множества точек. Гладкость входной поверхности сильно влияет на гладкость и адекватность получаемого решения.
Алгоритм имеет эвристическую природу, поэтому в данной статье не приводятся строгие математические доказательства существования и единственности найденного решения.
Постановка задачи
В декартовой прямоугольной системе координат на плоскости задана равномерная сетка:
где — узлы сетки;
— шаги сеток по оси
и
, соответственно. В каждом узле сетки задано значение
, представляющее собой высоту карты (ландшафта) местности в рассматриваемой точке. Значения
, образующие исследуемую поверхность, могут быть отрицательными — в таком случае высоту карты следует понимать как глубину относительно некоторой нулевой отметки
.
В качестве начального условия задана точка , которая может представлять собой крайнюю точку уже известного маршрута. Его необходимо продолжить далее через всю карту к плоскости
, рисунок 1.
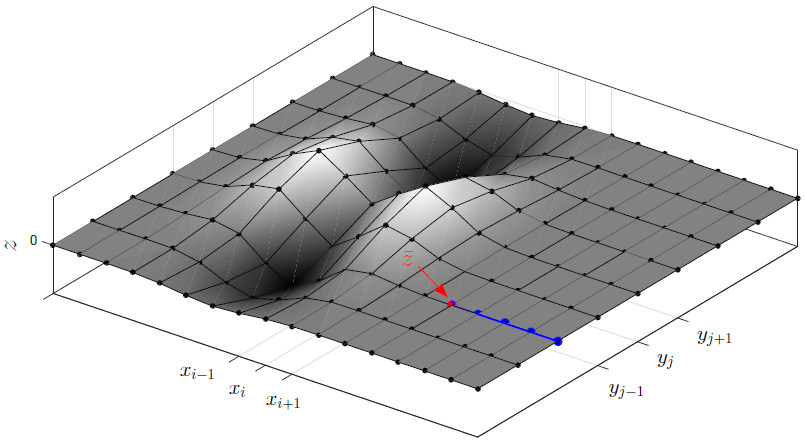 Рисунок 1. Пример ландшафта местности — исследуемая поверхность, заданная множеством точек. Синим цветом отмечена часть известного маршрута. Красная точка — начальное условие, точка из которой необходимо продолжить маршрут.
Рисунок 1. Пример ландшафта местности — исследуемая поверхность, заданная множеством точек. Синим цветом отмечена часть известного маршрута. Красная точка — начальное условие, точка из которой необходимо продолжить маршрут.
Численный алгоритм
Рассмотрим три ближайшие к соседние точки поверхности —
, находящиеся на соседнем слое по оси
. Одна из этих точек
лежит на том же слое по оси
, что и
, а остальные
лежат по диагонали к точке
, рисунок 2.
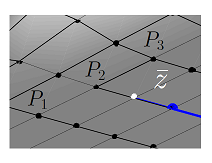 Рисунок 2. Соседние точки по оси Ox для начального условия.
Рисунок 2. Соседние точки по оси Ox для начального условия.
Вычислительный алгоритм построения оптимального маршрута является итерационным. На каждой итерации из трех соседних точек необходимо найти такую, сумма квадрата расстояния и квадрата тангенса угла наклона к которой является минимальной.
Для упрощения выкладок введем следующие обозначения:
— расстояние от точки
до точки
;
— тангенс угла, одна сторона которого — это отрезок, соединяющий
и
, а другая сторона — отрезок, соединяющий
и основание перпендикуляра, опущенного из точки
на плоскость перпендикулярную оси
и проходящую через точку
(углы
, рисунок 3).
 Рисунок 3. Схематический чертеж исследуемого множества точек. Начало искомого пути z, который необходимо продолжить и три соседние точки поверхности — P_1, P_2, P_3, из которых нужно будет вы-
брать одну, удовлетворяющую условию минимизации. Точки B_k — это основания перпендикуляров, опущенных из точек P_k
Рисунок 3. Схематический чертеж исследуемого множества точек. Начало искомого пути z, который необходимо продолжить и три соседние точки поверхности — P_1, P_2, P_3, из которых нужно будет вы-
брать одну, удовлетворяющую условию минимизации. Точки B_k — это основания перпендикуляров, опущенных из точек P_k
Таким образом, в данных обозначениях смысл вышеописанного алгоритма в следующем: используя начальное условие — последнюю точку известного маршрута, , нам необходимо найти такую точку
, чтобы выполнялось условие минимизации:
После нахождения данной точки необходимо принять ее в качестве начального условия для следующей итерации. В результате на каждой итерации мы будем получать новые точки искомого оптимального пути.
Смысл слагаемых в (1) следующий: первое слагаемое отвечает за выбор точки с наименьшим расстоянием до предыдущей, и, как следствие, для минимизации суммарной длины полученного маршрута; второе слагаемое в виде квадрата тангенса необходимо для минимизации перепада высот. Таким образом, вышеописанный алгоритм будет прокладывать маршрут, стараясь обходить все локальные экстремумы, что мы и увидим в
экспериментах. Вместо тангенса можно было бы с тем же успехом использовать синус, что никак не повлияет на результат работы алгоритма.
В процессе расчетов может оказаться, что точкабудет находиться на крайнем слое по оси
(
или
) — в таком случае необходимо рассматривать не три соседние точки
, а две — одна из которых лежит «по прямой», а другая «по диагонали» к точке
, при этом алгоритм построения оптимального маршрута никак не изменится.
Сложность алгоритма составляет и зависит от «длины» карты, на которой необходимо проложить искомый маршрут. На каждой итерации необходимо проверять по 2–3 точки и находить минимальное значение (1).
Реализация алгоритма
Исходники находятся здесь
Определим свой класс для точки в пространстве:
class Point3D:
def __init__(self, N, M, z, PositionalParameter):
self.N = N
self.M = M
self.z = z
self.PositionalParameter = PositionalParameterДля удобства вместо и
я использовал
и
, соответственно.
PositionalParameter будет равен единице для точек и нулю для точки
дабы немного упростить вычисления квадратов, упомянутых в формуле (1).
Определим функцию для подсчета квадрата расстояния:
def GetSquareOfDistance(point, testedPoint, dy):
"""Возвращает относительный квадрат расстояния до проверяемой точки"""
return math.pow(point.z - testedPoint.z, 2.0) + testedPoint.PositionalParameter * dy * dypoint — это точка ,
testedPoint — точка ,
— шаг по оси
.
На самом деле здесь не совсем квадрат расстояния, а немного упрощенное значение, которое не учитывает шаг , т.к. для поиска минимального значения в (1) его можно выкинуть (предоставлю читателю возможность это проверить).
А также функцию для подсчета квадрата тангенса:
def GetTangentSquare(point, testedPoint, dx, dy):
"""Возвращает квадрат тангенса угла между точками"""
return math.pow(point.z - testedPoint.z, 2.0) / (dx * dx + testedPoint.PositionalParameter * dy * dy)В отдельном файле были определены функции для формирования поверхностей как функции двух переменных:
import math
# Возвращает сумму квадрата синуса первого аргумента и квадрата косинуса второго аргумента
# x - первый аргумент
# y - второй аргумент
def SinSquarePlusCosSquare(x, y):
return math.sin(x) * math.sin(x) + math.cos(y) * math.cos(y)
# Функция Гаусса (двумерная гауссиана).
# Описание параметров (раздел "Многомерные обобщения"): https://ru.wikipedia.org/wiki/%D0%93%D0%B0%D1%83%D1%81%D1%81%D0%BE%D0%B2%D0%B0_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F
# x, y - точка плоскости, в которой необходимо вычислить Гауссиан
# A - высота колокола
# sigmaX, sigmaY - размах колокола по оси Ox и Oy, соответственно
# x0 - сдвиг пика по оси Ox
# y0 - сдвиг пика по оси Oy
def Gaussian(x, y, A, sigmaX, sigmaY, x0, y0):
xx = (x - x0) * (x - x0) / (2.0 * math.pow(sigmaX, 2.0))
yy = (y - y0) * (y - y0) / (2.0 * math.pow(sigmaY, 2.0))
return A * math.exp(-(xx + yy))Гауссиан отлично подходит для имитации отдельно стоящей горы. А с помощью композиции можно создавать горные цепи разной длины и сложности. SinSquarePlusCosSquare создает, как Вы уже догадались, подобие холмистого рельефа.
В конце расчета маршрут записывается в файл как массив трехмерных точек.
Результаты численного решения
На следующих рисунках показаны результаты численных экспериментов нахождения оптимальных маршрутов. Для имитации ландшафта местности использовались различные аналитические поверхности. Все размерности даны в условных единицах, шаг сеток во всех расчетах по обеим осям был взят равным
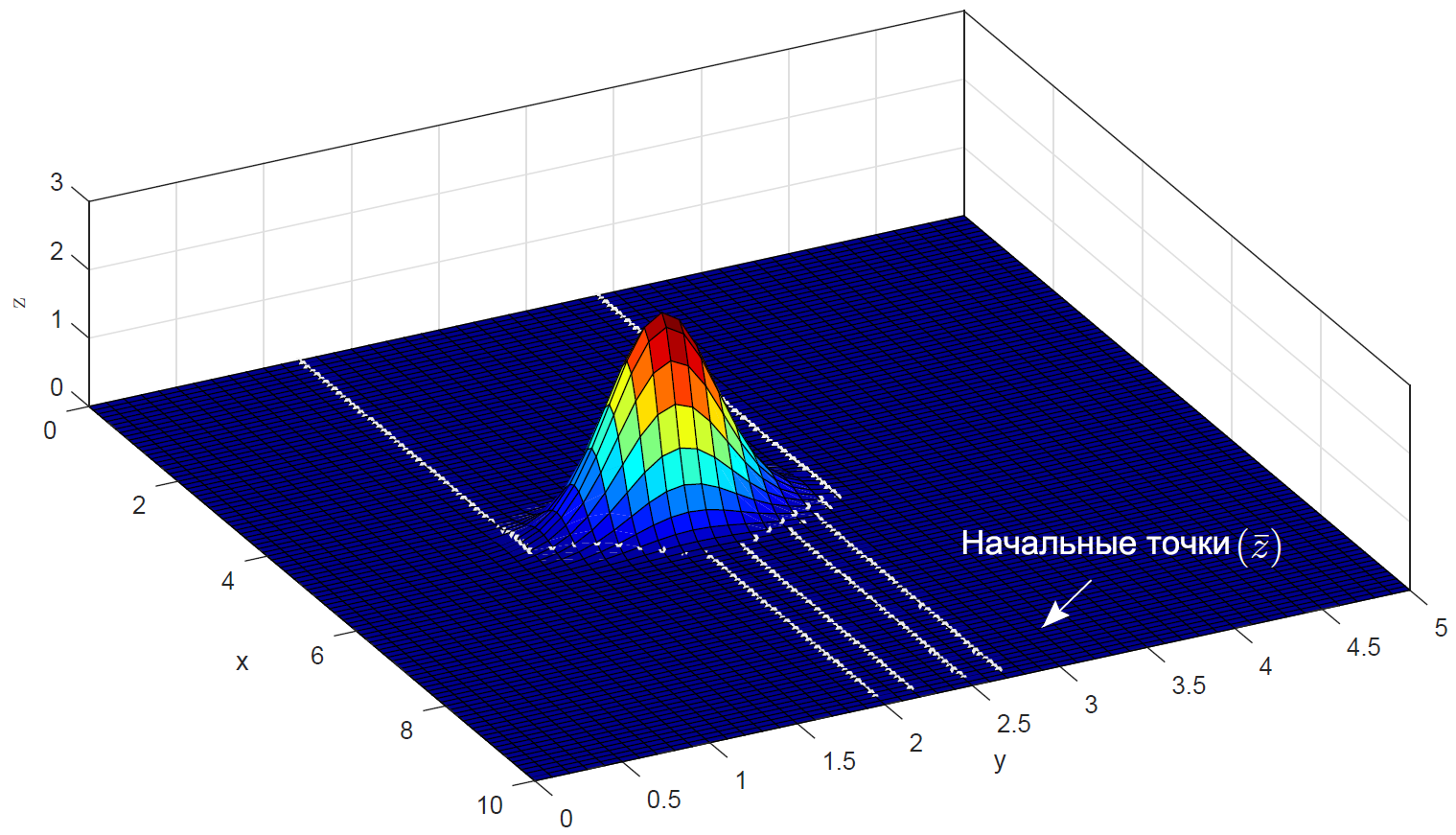 В качестве имитации горы использовалась функция Гаусса.
В качестве имитации горы использовалась функция Гаусса.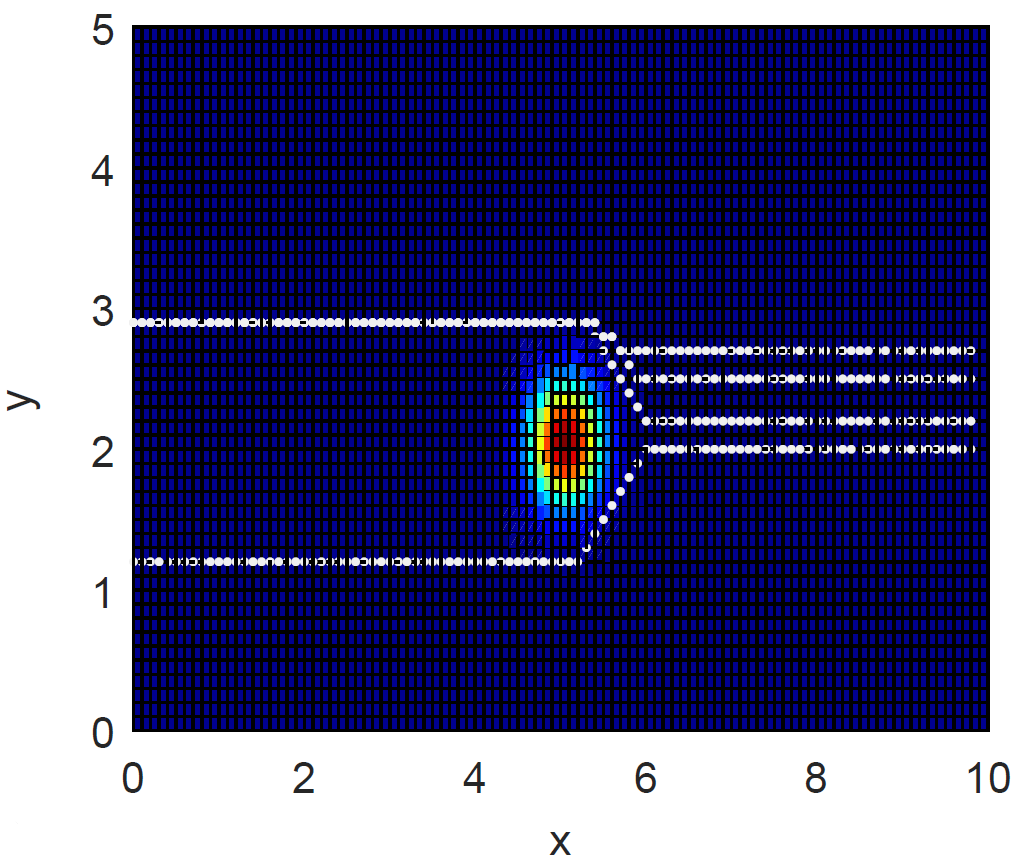 А это вид сверху
А это вид сверху
Холмистый рельеф. Имитация с помощью функции
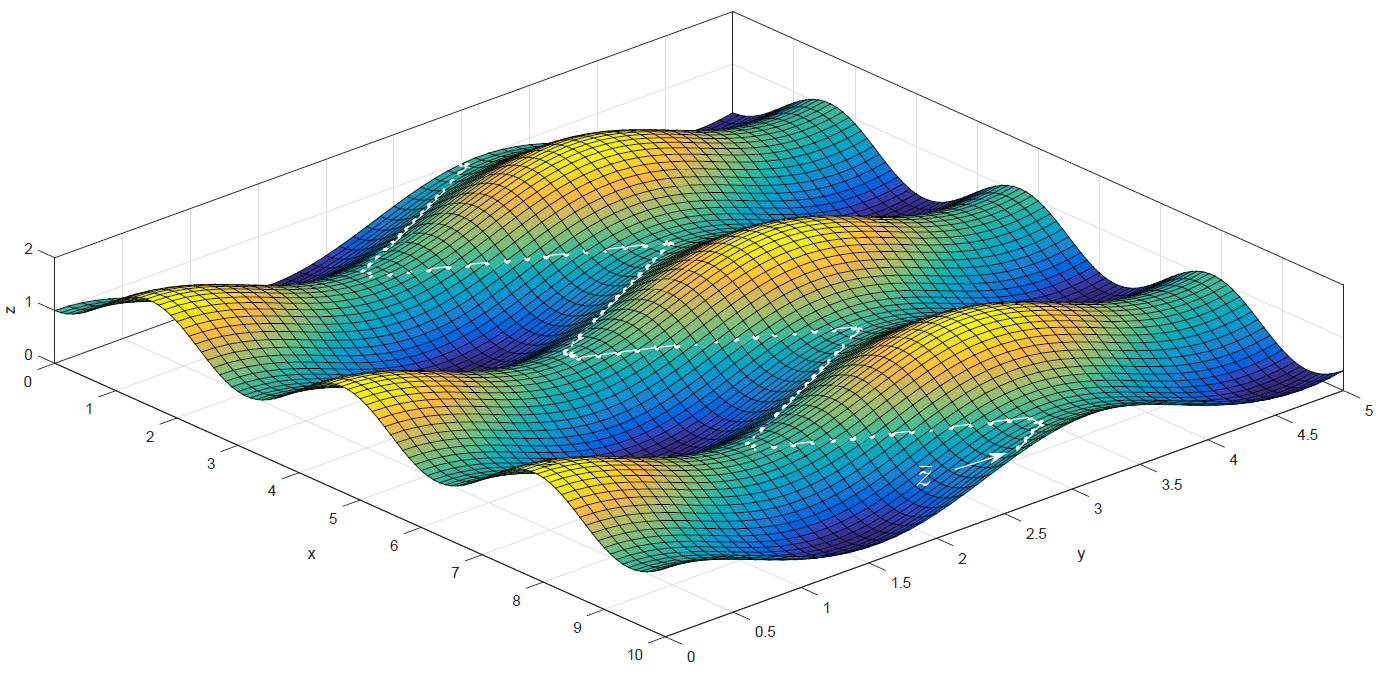 Имитация холмистого ландшафта. Хорошо видно как маршрут (белая линия) обходит локальные экстремумы.
Имитация холмистого ландшафта. Хорошо видно как маршрут (белая линия) обходит локальные экстремумы.
а это вид сверху:
 Вид сверху
Вид сверху
Вот еще один интересный вариант ландшафта. Наложение нескольких функций Гаусса и поверхности заданной формулой :
 Горы и впадины
Горы и впадины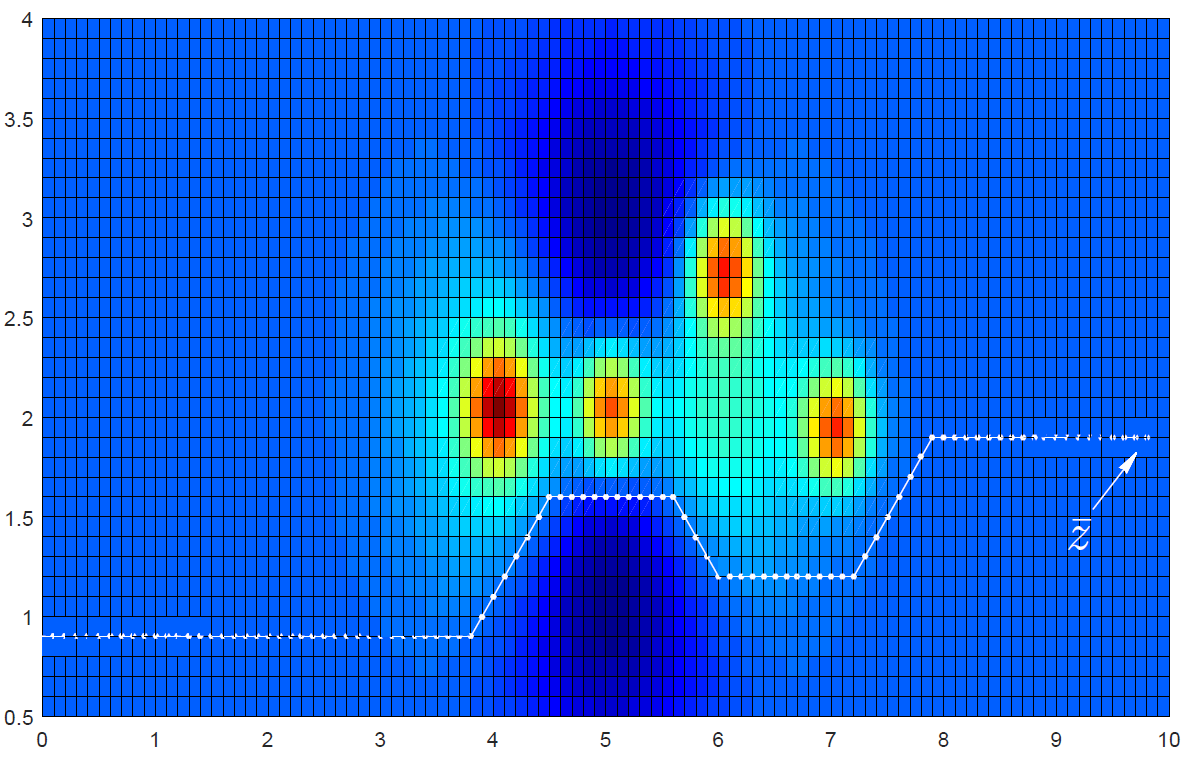 Вид сверху
Вид сверху
Спасибо за прочтение!
Все доработки и усовершенствования оставляю Вам.
