Учимся квантовому программированию на Python с помощью примеров. Доклад Яндекса09.07.2020 15:02

Сегодня любой желающий может воспользоваться методами квантового программирования, написать простой код на Python и запустить его на реальном квантовом вычислителе. Ришат Ибрагимов rishat_ibrahimov разобрал основы квантовых вычислений на примерах с кодом, показал, как запускать программы на локальном симуляторе и удаленном квантовом компьютере.

— Всем привет, меня зовут Ришат. Я почти три года работаю над качеством поиска Яндекса. Но поговорить сегодня хочу не о работе, а о том, чем я занимаюсь в свободное время. Занимаюсь я квантовой информатикой, а на самом деле — самыми разными моделями вычислений, в том числе квантовыми.
Квантовая информатика — это сейчас достаточно интересная область. Туда много сил вкладывается, много всего сделано. В докладе я постараюсь заинтересовать кого-то из вас. Может быть, среди вас есть крутой ML-инженер, который захочет заниматься квантовым машинным обучением, или просто сильный алгоритмист, который сможет вложить свои силы в это направление. Будет здорово, потому что будущее скоро наступит.

Сразу скажу, что я не физик. Наверняка среди вас есть люди, которые в физике всех этих процессов понимают больше, чем я. Поэтому про физику я не буду говорить почти ничего.

От вас я жду, что вы совсем немножко помните алгебру, помните, что такое вектор и как умножить вектор на матрицу.

Как будет построен мой доклад? Сначала мы поговорим немного об истории, о том, откуда все взялось, чтобы уверенно смотреть в будущее. Потом посмотрим, где это можно применять, какое сейчас состояние, можно ли прямо сейчас что-то делать руками. Мы напишем первую программу на Python, которую можно будет запустить на квантовом компьютере. И потом в качестве бонуса я вам покажу несколько примеров алгоритмов, в которых квантовые вычисления помогают добиться несравненно лучшей производительности по сравнению с классическими.

С чего все началось? Вот с этого молодого человека. Это Алан Тьюринг, его можно смело назвать отцом информатики или компьютерных наук, того, за счет чего мы все сейчас живем, зарабатываем деньги. В 30-х Тьюринг придумал модель вычислений, которую мы бы сейчас назвали программируемый компьютер. А вот этого человека кто-нибудь узнает?

Уже сложнее. Его фамилия очень часто идет рядом с фамилией Тьюринга. Это Алонзо Чёрч, он тоже занимался проблемами вычислимости, и даже немножко раньше Тьюринга придумывал свои модели вычислений. Но более популярными стали работы Тьюринга. И вообще, Чёрч в какой-то момент был научным руководителем Тьюринга. Взятые вместе, их фамилии обычно связывают вот с этим тезисом.

Тезис Чёрча-Тьюринга говорит: любой процесс может быть эффективно смоделирован на машине Тьюринга. Это конец 30-х — начало 40-х, и все очень хорошо. Примерно 30 лет всё очень хорошо, пока не появились вот эти два человека. Кто-нибудь их знает?

Это уже 70-е, совсем близко к современности. Их фамилии часто встречаются в курсах криптографии. Это Роберт Соловей и Фолькер Штрассен. Эти два человека знамениты тем, что они придумали вероятностный алгоритм проверки числа на простоту, тест Соловея-Штрассена.

И это очень важный момент для нас, потому что до сих пор мы говорили, что любой алгоритмический процесс можно смоделировать на машине Тьюринга. Но сейчас получается, что их алгоритм смоделировать нельзя. Он вероятностный, в машине Тьюринга ничего такого нет.

Пришлось сделать быстрофикс и сказать, что любой процесс можно смоделировать на вероятностной машине Тьюринга. Это уже не очень круто, наверняка у кого-то из вас в груди тоже защемило. Вы подумали: как же так? Сейчас мы говорим «вероятностный», через десять лет откроют еще что-нибудь, придется еще что-нибудь править. Это не очень приятно. Но мы с вами, конечно, не одни такие.

Был еще один молодой человек — Дэвид Дойч. И он тоже задавался вопросом: как же так? Как же жить? Он физик по образованию, всю жизнь посвятил физике. И решил заняться этой проблемой именно с точки зрения физики. Он сказал: давайте попробуем обосновать, получить какой-нибудь такой, чтобы сама природа нам говорила о том, что это именно так. А природа уже тогда говорила (и мы до сих пор считаем), что она квантово-механическая. Поэтому мы начали искать ответ в квантовой механике. И именно с Дэвида Дойча, с его первых алгоритмов, началась квантовая информатика.

Это такой небольшой экскурс в историю, чтобы вы понимали: это взялось не на ровном месте. В этой облассте есть реальные проблемы, теоретические, конечно, которые мучают людей, с которых все началось.

Но всё ли только на уровне теории? По большому счету, с точки зрения математики никаких проблем не осталось. С точки зрения математики мы знаем все о том, как должен работать квантовый компьютер. Сейчас уже есть настоящие квантовые компьютеры разных конфигураций, по-разному работающие. И это, по большому счету, инженерная задача.

Например, у нас в институте есть целое отделение, которое занимается квантовой информатикой. Там есть и математики, и физики. Физики сейчас очень плотно занимаются проблемой долгосрочного хранения квантовой информации. Это очень похоже на наши жесткие диски, но хочется, чтобы там хранилась квантовая информация.

Какие же могут быть применения у всего этого хозяйства? Конечно, первое, что приходит в голову, — это моделирование процессов, потому что мир устроен квантово-механически. И если мы будем использовать квантовый компьютер, чтобы моделировать процессы, химические реакции или еще что-нибудь, это будет стоить намного дешевле с точки зрения вычислений.

Второй и очень большой раздел, которому сейчас посвящено много сил, — квантовое машинное обучение. Есть очень большая надежда, что квантовые вычисления помогут ускорить сами процессы обучения и усовершенствовать алгоритмы. Тут очень много работы. Сейчас, например, наша квантовая группа работает вместе с одним ученым из Китая. Он очень сильный ML-инженер, а мы немного с квантовым уклоном, пытаемся что-то вместе придумать.

Третья штука несколько месяцев назад была немного хайповая. Сейчас, может, хайп уже спал, но есть даже целый квантовый блокчейн. Его придумал мой хороший друг и большой товарищ. Это я так, немного с гордостью говорю.

Но квантового компьютера у нас нет. К сожалению, мы не можем прийти домой и так же просто, как мы программируем на Python, запустить программы.

Что делать? О том, что делать, я думал еще на третьем курсе, когда писал свою первую курсовую работу. Я писал эмулятор квантовых вычислений. Конечно, все пишут эмуляторы и все ими как-то пользуются. На четвертом курсе я писал эмулятор, который имитирует помехи, шумы и всякое прочее. А потом мне надоело.

Я попробовал поискать в поисковике и понял, что эмуляторов много. Здесь несколько ссылок, они достаточно простые и интересные:

Но я хочу остановиться на qiskit. Он особенный, выделяется из всех. Чем?

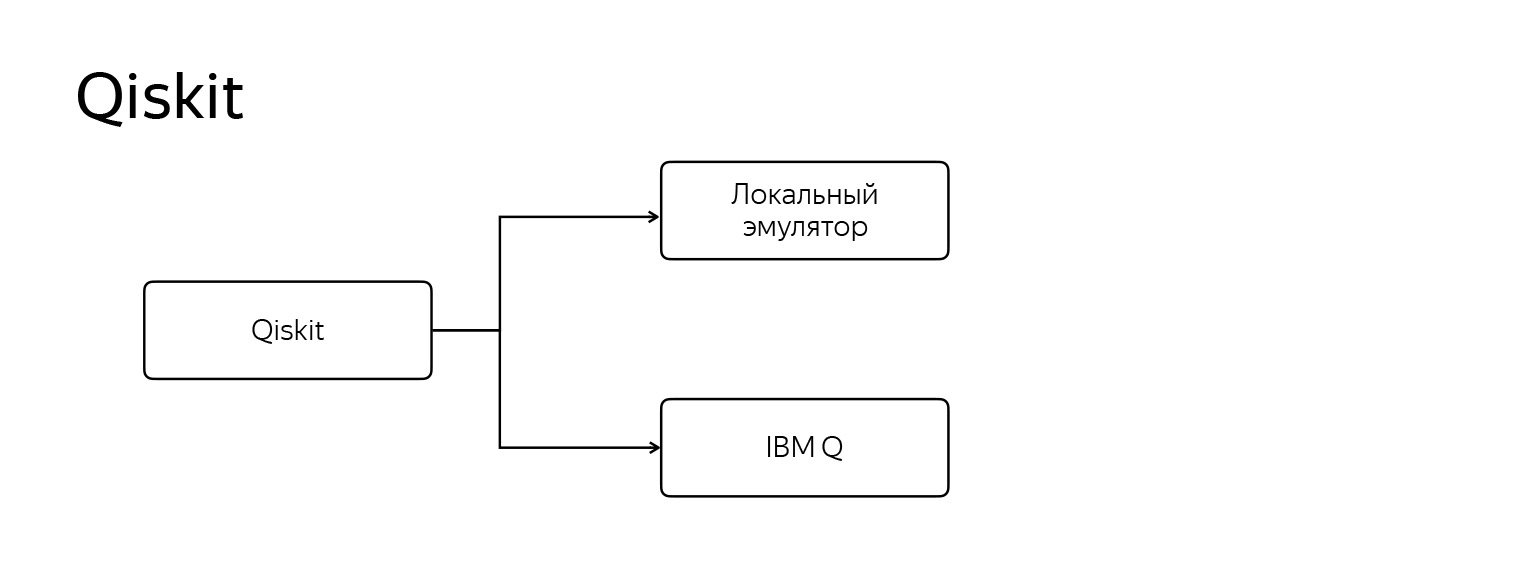
Он работает в двух режимах. Первый — как и все, обычный локальный эмулятор. Второй — запуск вашей программы на настоящем квантовом компьютере IBM Q, который выглядит примерно так.

Сейчас это целая бочка, в которой поддерживается экстремально низкая температура — порядка трех милликельвин. Это очень холодно. И IBM предоставляет возможность с помощью облачных технологий подключиться и запустить ваш код прямо на этой машине.

Конечно, он специальным образом компилирует туда команды и все прочее. Как это вообще работает? Для общего доступа есть несколько инсталляций такого компьютера. Один из них 5-кубитный, есть 15-кубитный, 16-кубитный, нам доступны даже 20 кубит. Это примерно как 20 бит обычной, классической информации, но уже что-то.

Тут наверняка многие из вас думают: все, хочу! Но придется немного вспомнить математику. Немного алгебры, но совсем чуть-чуть, как я и обещал.

Чтобы начать программировать на квантовом компьютере, нужно понять, что вообще такое кубит. Это просто вектор в двумерном векторном пространстве. Но раз уж мы говорим о векторных пространствах, в них есть базис.

Базис выглядит примерно так. Есть два векторных столбца и единичный базис, стандартный, в курсах алгебры его так обозначают:

и 

. И есть стандартное обозначение в нотации Дирака, вот в таких угловых скобочках.

То есть, чтобы вы не путались, сокращать я дальше буду так.

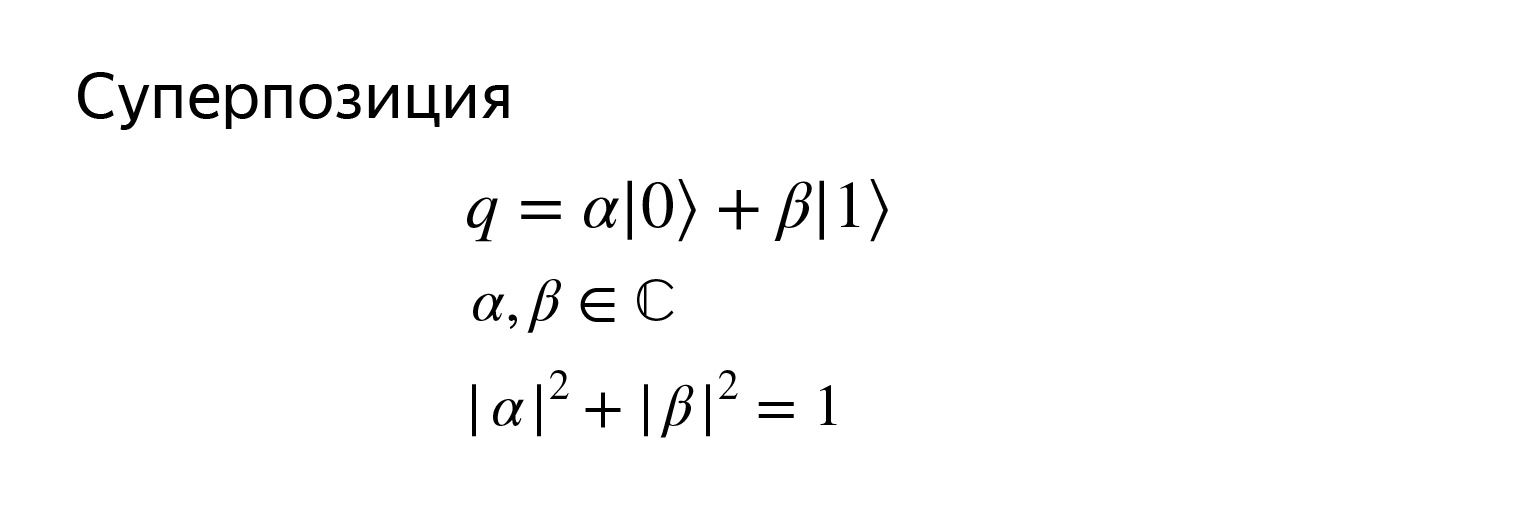
И поскольку это вектор, его состояние можно записать так. Кубит q — это суперпозиция двух базисных векторов, где α и β — комплексные чиселки, но не совсем любые, а чтобы сумма модулей их квадратов была равна единице.

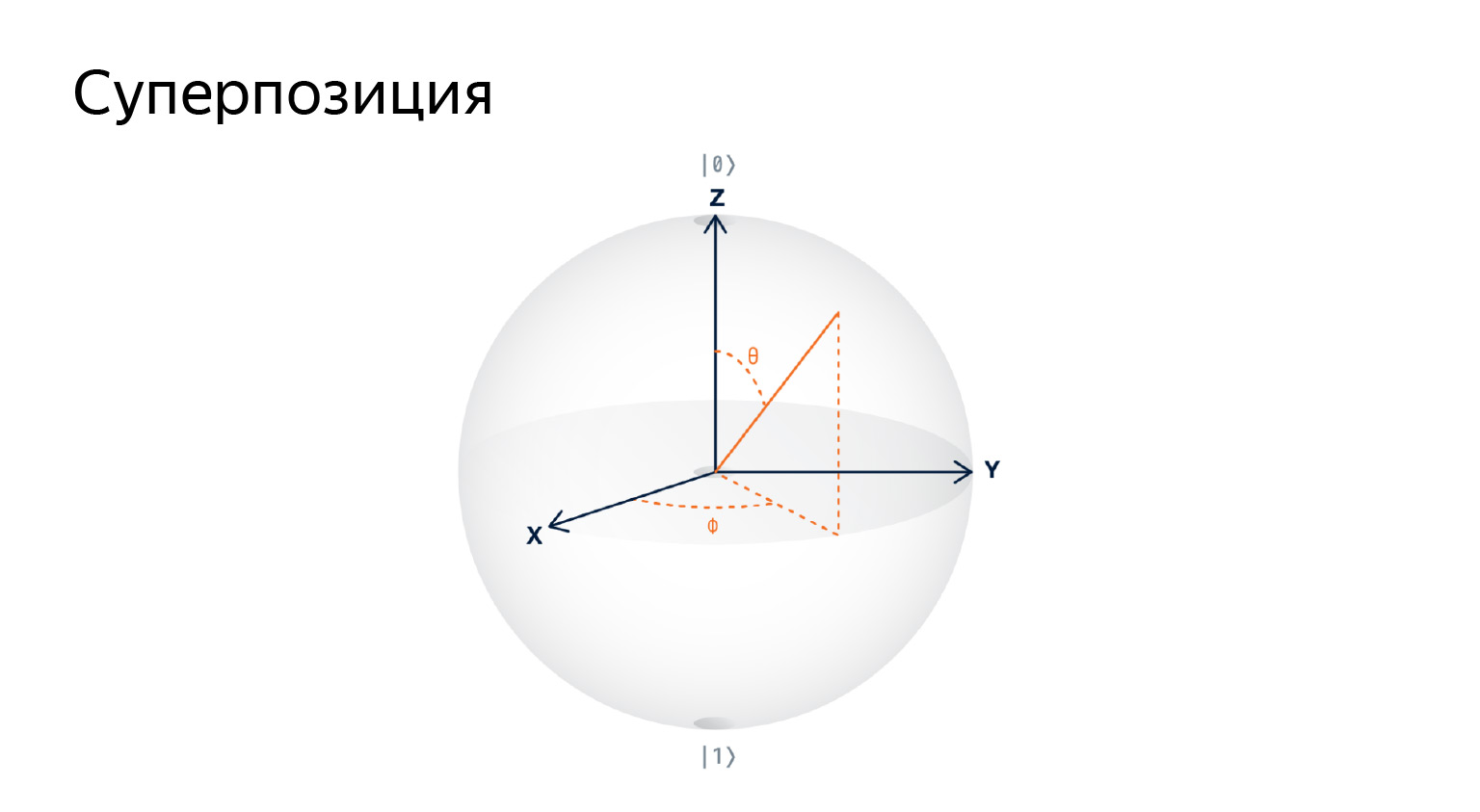
Если эту штуку попробовать нарисовать, мы получим, что кубит — это вектор на трехмерной сфере. В одном кубите может храниться бесконечно много информации, ведь это просто вектор, которого бесконечно много.

Можно не обращать внимания на картинку, это просто способ визуализации для привлечения внимания.

Про кубиты поговорили. Самое главное, что кубит — это вектор. Вектор в комплексном векторном пространстве. Что с ним можно делать?

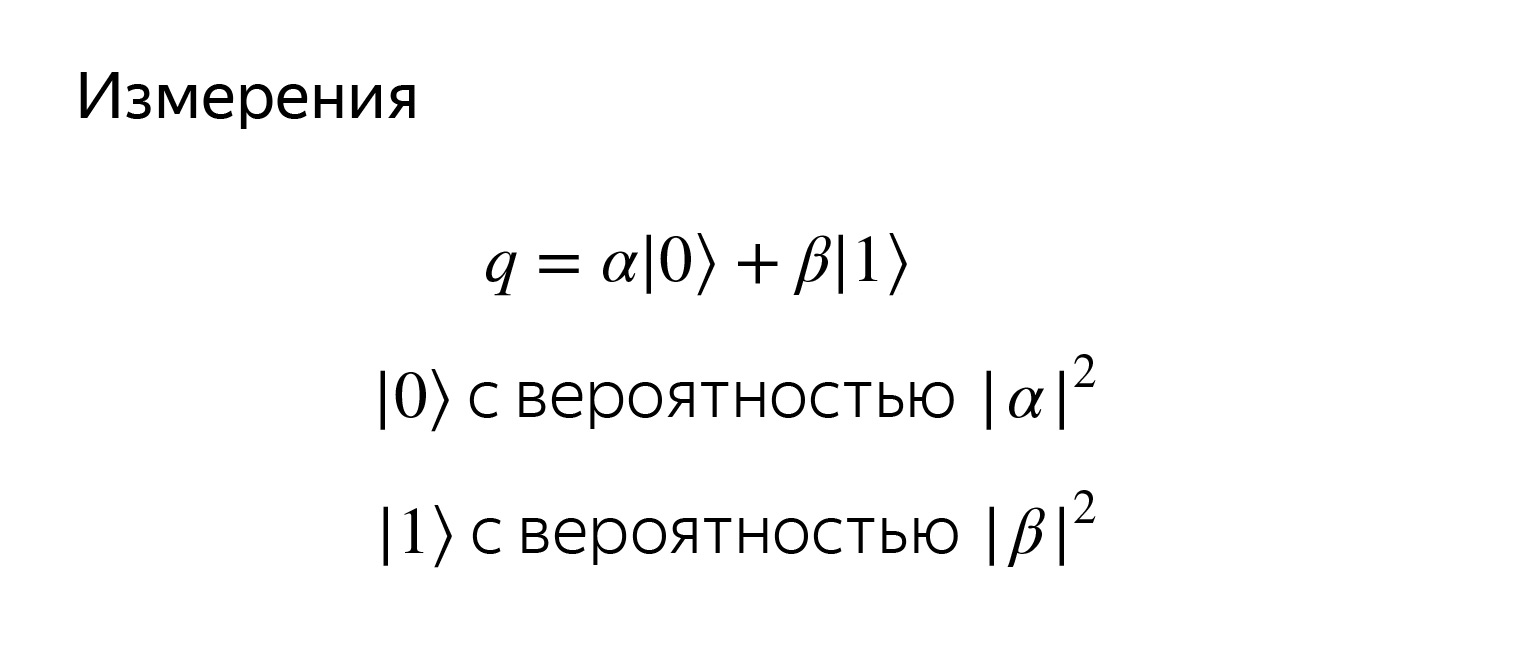
Первое, что мы привыкли делать, — попробовать посчитать значение нашей переменной, например, в Python. Мы хотим прочитать, в каком состоянии находится кубит. Но мы никогда не узнаем точные значение α и β.

Если мы попробуем посмотреть на кубит, прочитать, то мы получим или нолик, или единичку с соответствующими вероятностями. Вероятности –—это просто проекции на соответствующие базисные вектора.

Второе, что мы можем делать, — например, склонировать кубит. Мы такое называем присваиванием одной переменной другой. В квантовом мире так делать нельзя, к сожалению.

Операции присваивания нет, и это очень связано с тем, о чем я говорил только что: мы даже не сможем посмотреть точное значение. Это фундаментальный результат. Доказывается он очень просто: буквально две строчки сравнений, от противного.

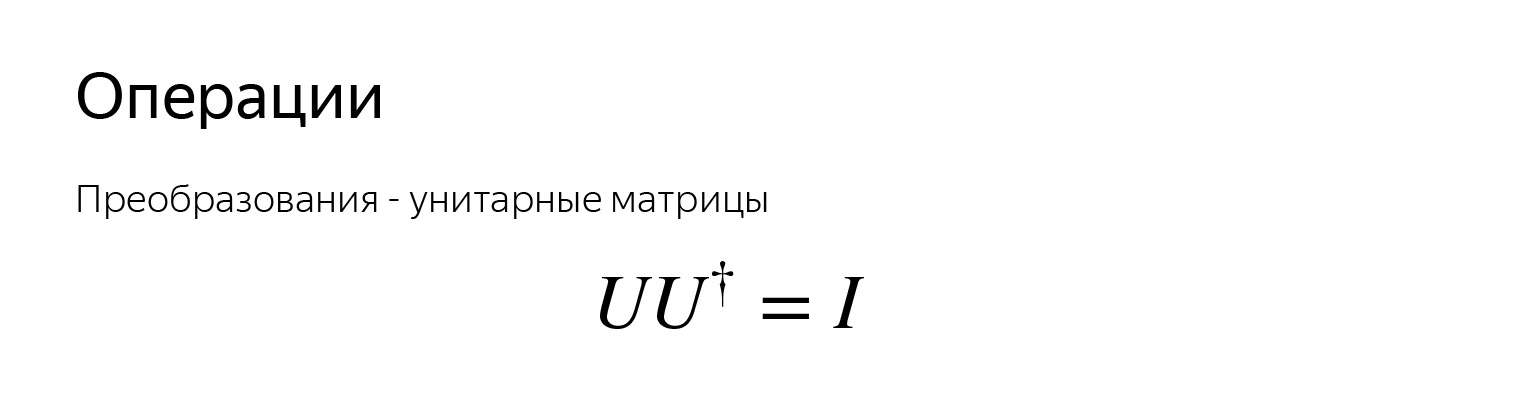
Есть кубит, который мы не можем прочитать, не можем склонировать. Что можно вообще делать?

Кубит — это вектор. Вектор можно взять и покрутить по сфере вокруг. Чтобы покрутить, можно придумать матрицу, которая это вращение делает. Все операции над кубитами — это матрицы. Они называются унитарными.

Унитарные — чтобы выполнялось такое условие, оно тут записано хитрым образом. Этот значок означает транспонированную и комплексно-сопряженную матричку. Свойство очень важное, оно означает, что для любой операции есть обратная. То есть как бы мы ни покрутили вектор, мы всегда можем его вернуть в прежнее положение. Всегда существует обратная операция.

Посмотрим, какие операции могут быть. То, к чему мы привыкли в классическом случае. Есть нолик, можно превратить его в единичку и наоборот.

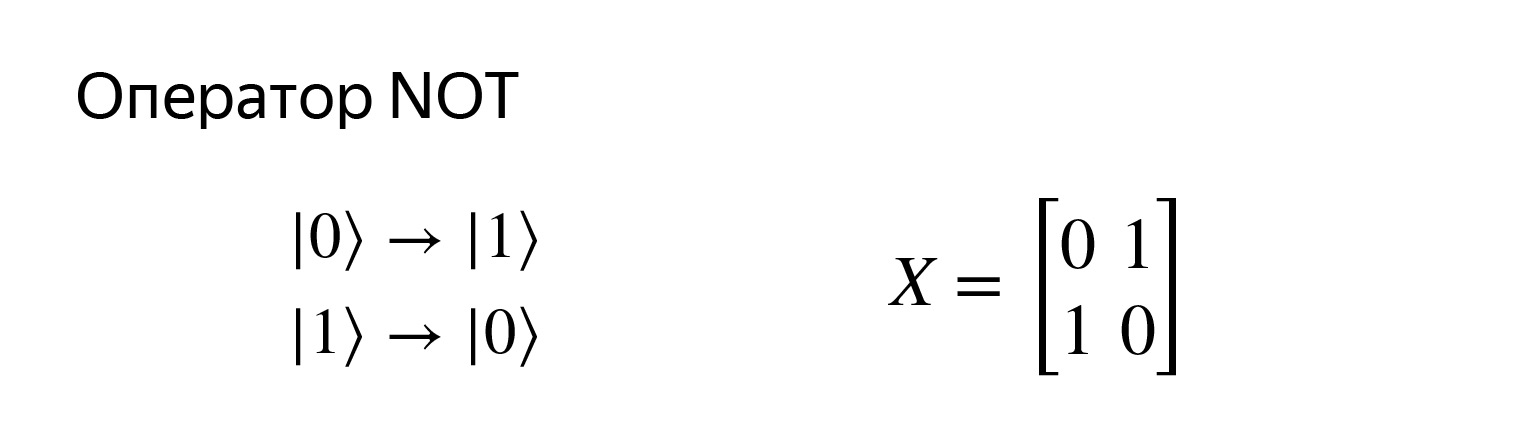
Это оператор отрицания, он очень простой. Записывается вот такой матричкой. Если мы попробуем перемножить, получим ровно то, что хотим.

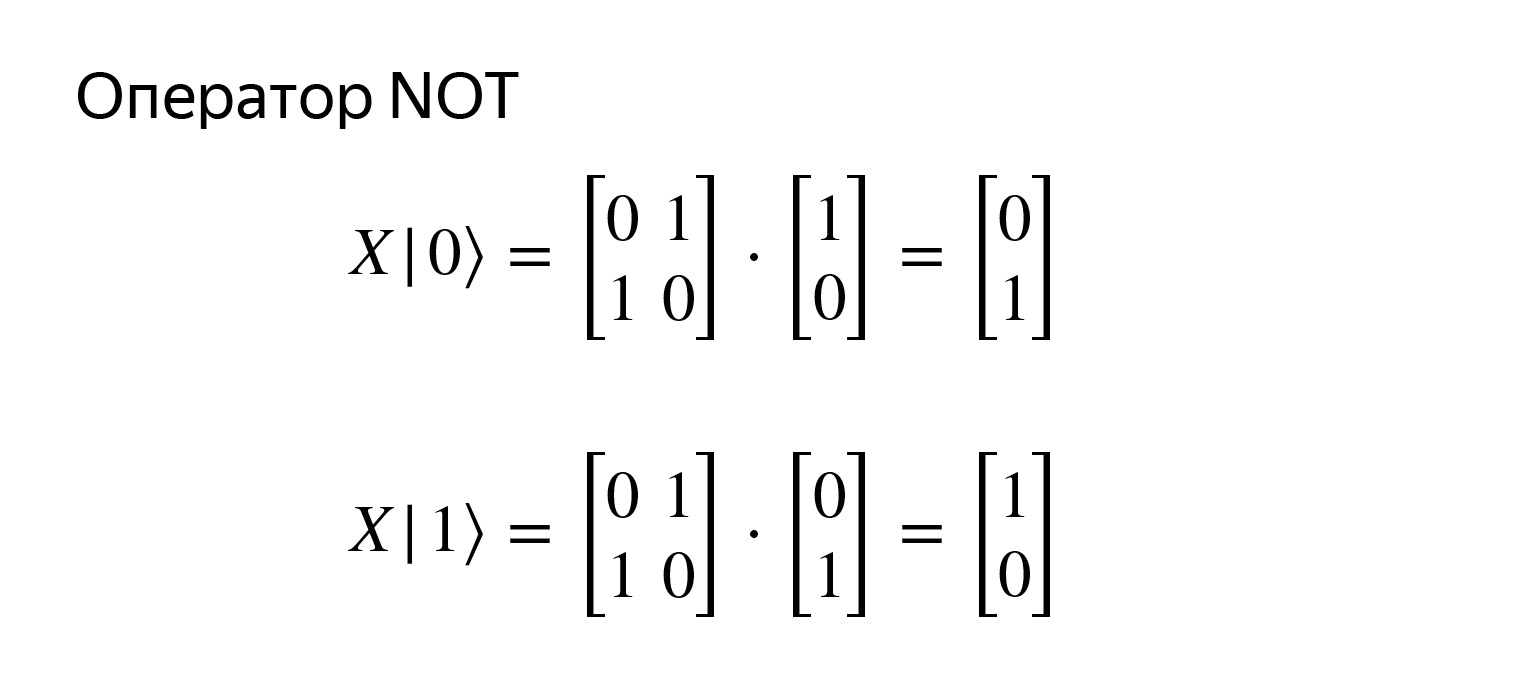
У меня тут даже нарисовано. Ничего сложного. У оператора отрицания есть стандартная запись, оператор X. Если подумать, это просто вращение вокруг одной из осей. И есть операторы Y и Z, вращение вокруг других осей, но это сейчас не так важно.

И мы уже можем запустить нашу первую программу на квантовом компьютере, которая будет делать отрицание кубита.

Но мы в квантовой информатике, конечно, очень редко пишем на Python. Чаще мы пользуемся схемами.

Схема обычно выглядит так. Горизонтальные линии — это просто значения кубит. У меня тут их нарисовано пять. А в блоке — операция, которую мы будем делать.

Первый блок. Здесь нарисован измерительный прибор. Это значит, что мы просто хотим измерить, что же находится в первом кубите.

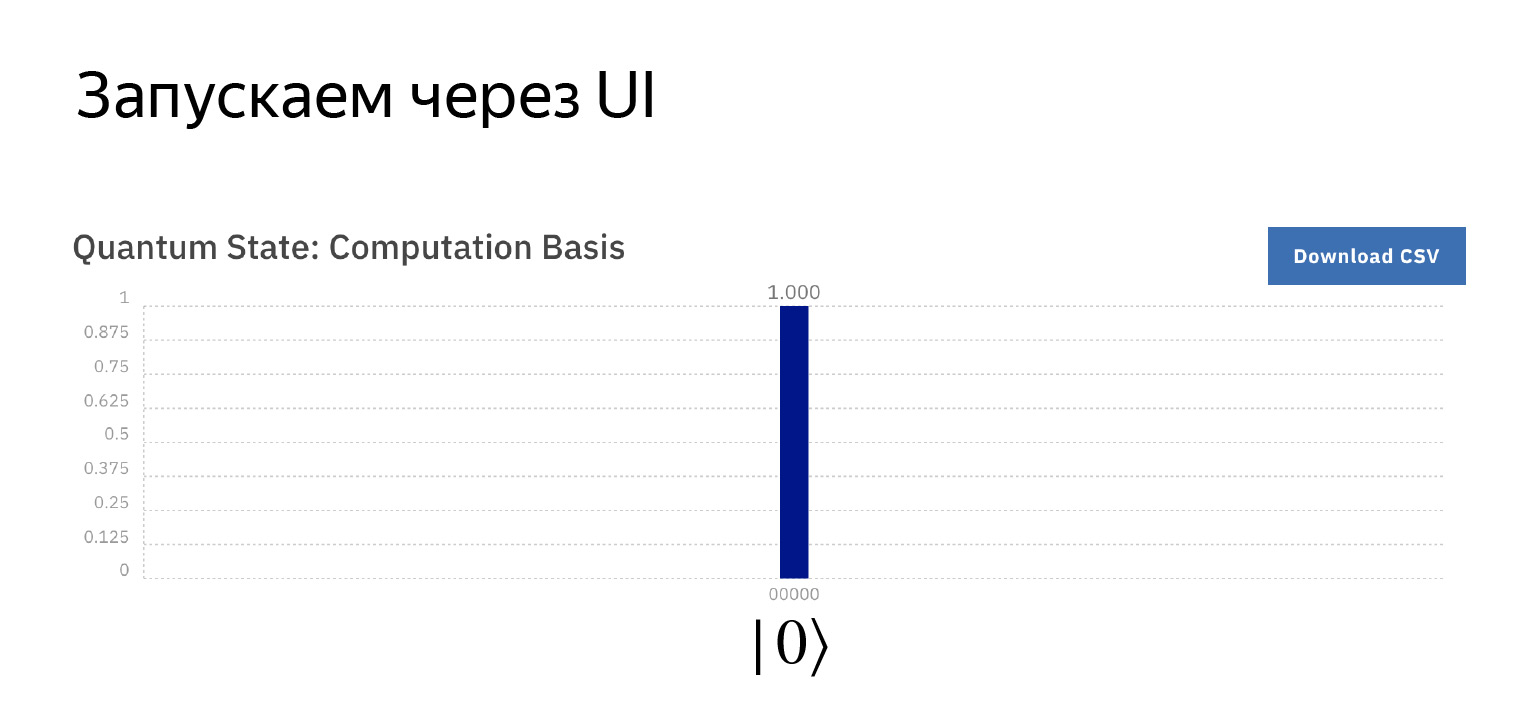
Если мы эту штуку запустим, то получим, что с вероятностью единичка у нас там стоит нолик, потому что они инициализированы в таком состоянии и мы больше ничего с ними не делали.

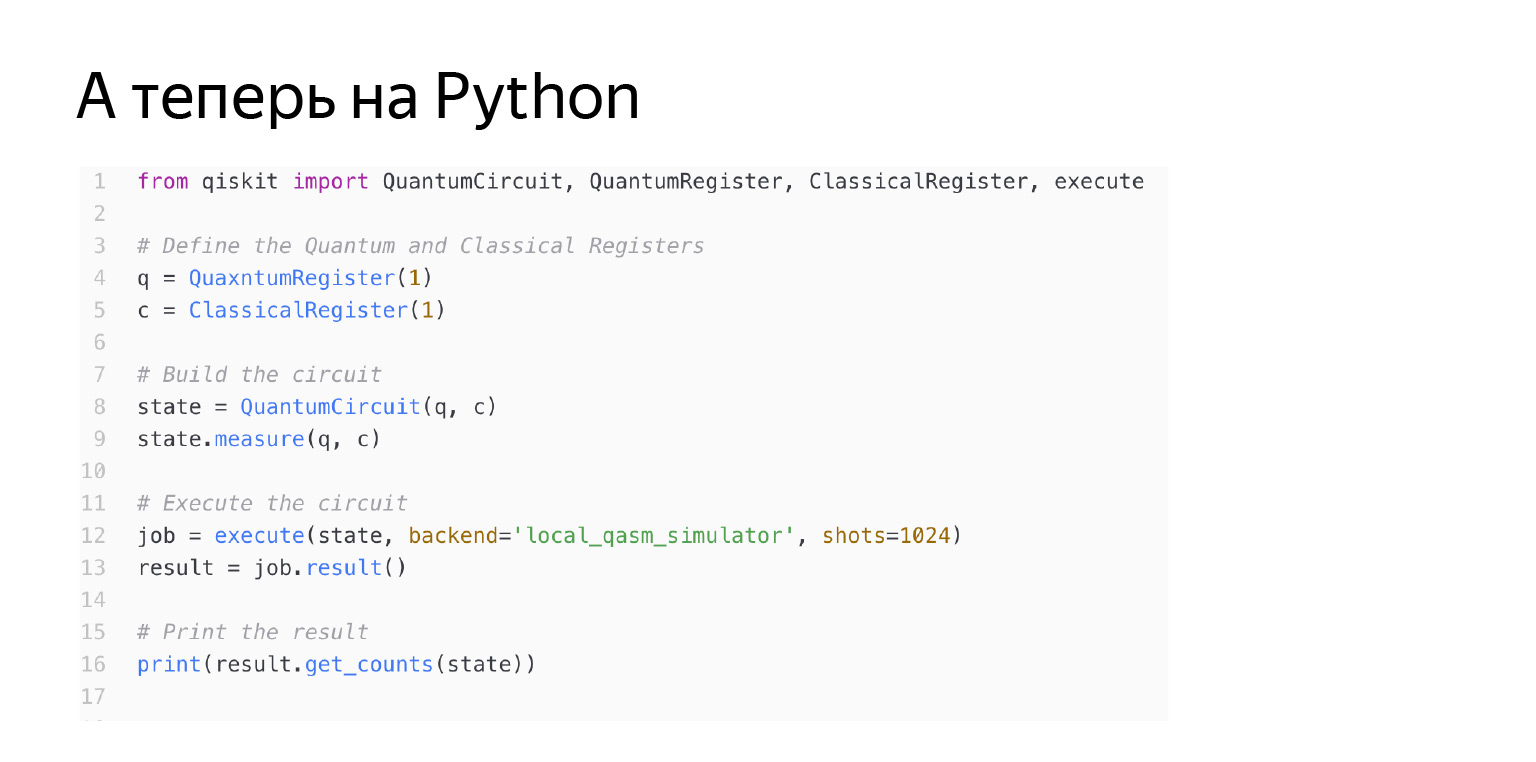
Такую штуку можно написать на Python с помощью библиотечки qiskit. Давайте по строчкам посмотрим, что здесь происходит. Сначала мы заводим квантовый регистр. Я здесь завожу его из одного кубита. И классический регистр. Классический регистр нужен, чтобы куда-то записать результат измерения. То есть я с квантовым регистром делаю преобразования, результат получаю классический — нолик или единичку. И потом создаю свою схему, в которой есть этот квантовый классический кубит. Я просто говорю: давайте измерим кубит q в C. Запустим все это дело, и все будет хорошо. Но внимательный читатель увидит: здесь написано, что у меня backend — это локальный эмулятор.

То же самое можно сделать и с IBM Q, но здесь чуть больше кода. Здесь всякая лапша по поводу того, чтобы выбрать девайс, который нам побыстрее ответит, токены какие-то передать, вот это все. Но ничего хитрого нет.

То же самое можно сделать с оператором отрицания. Это оператор X, как я сказал. На схеме выглядит точно также, запустим то же самое.

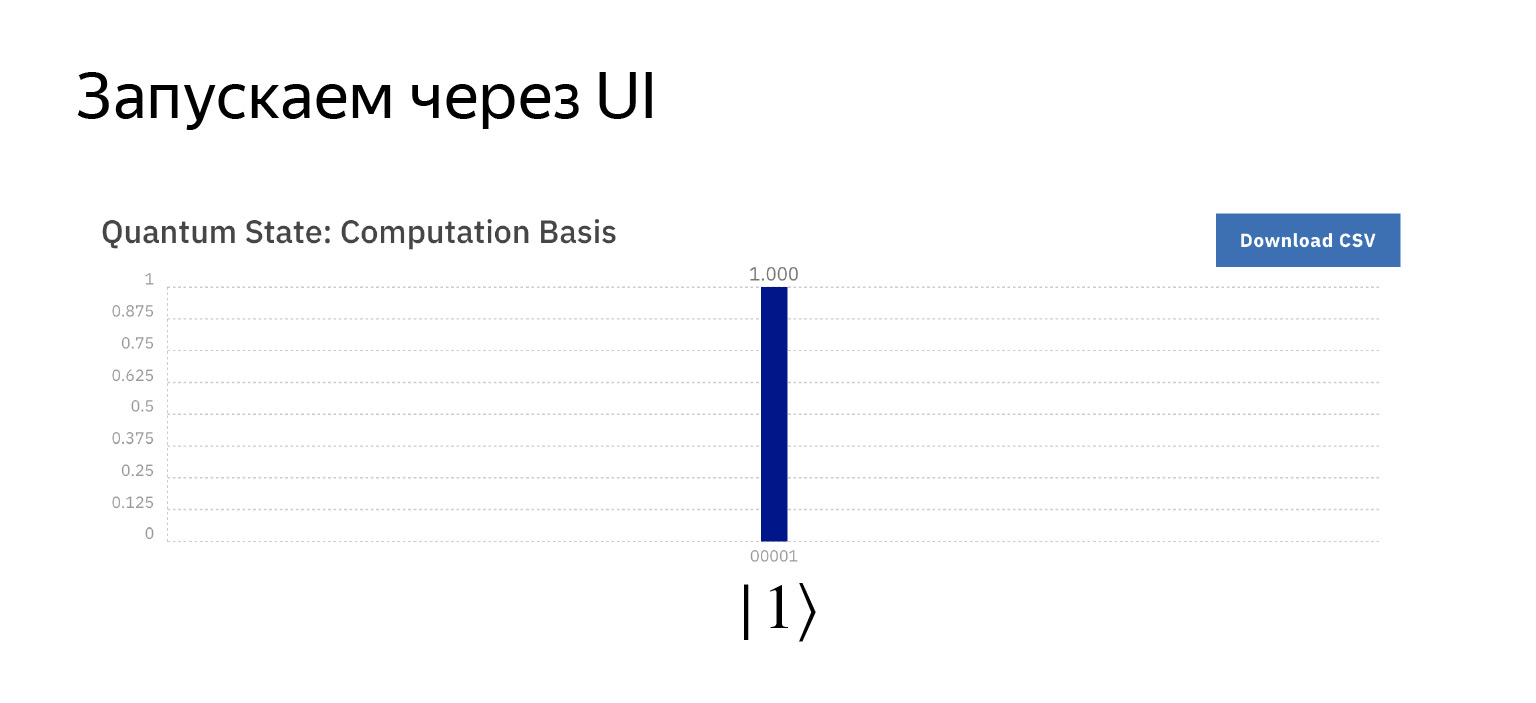
Теперь с вероятностью единичка получим единичку, как и планировали. Никакой магии.

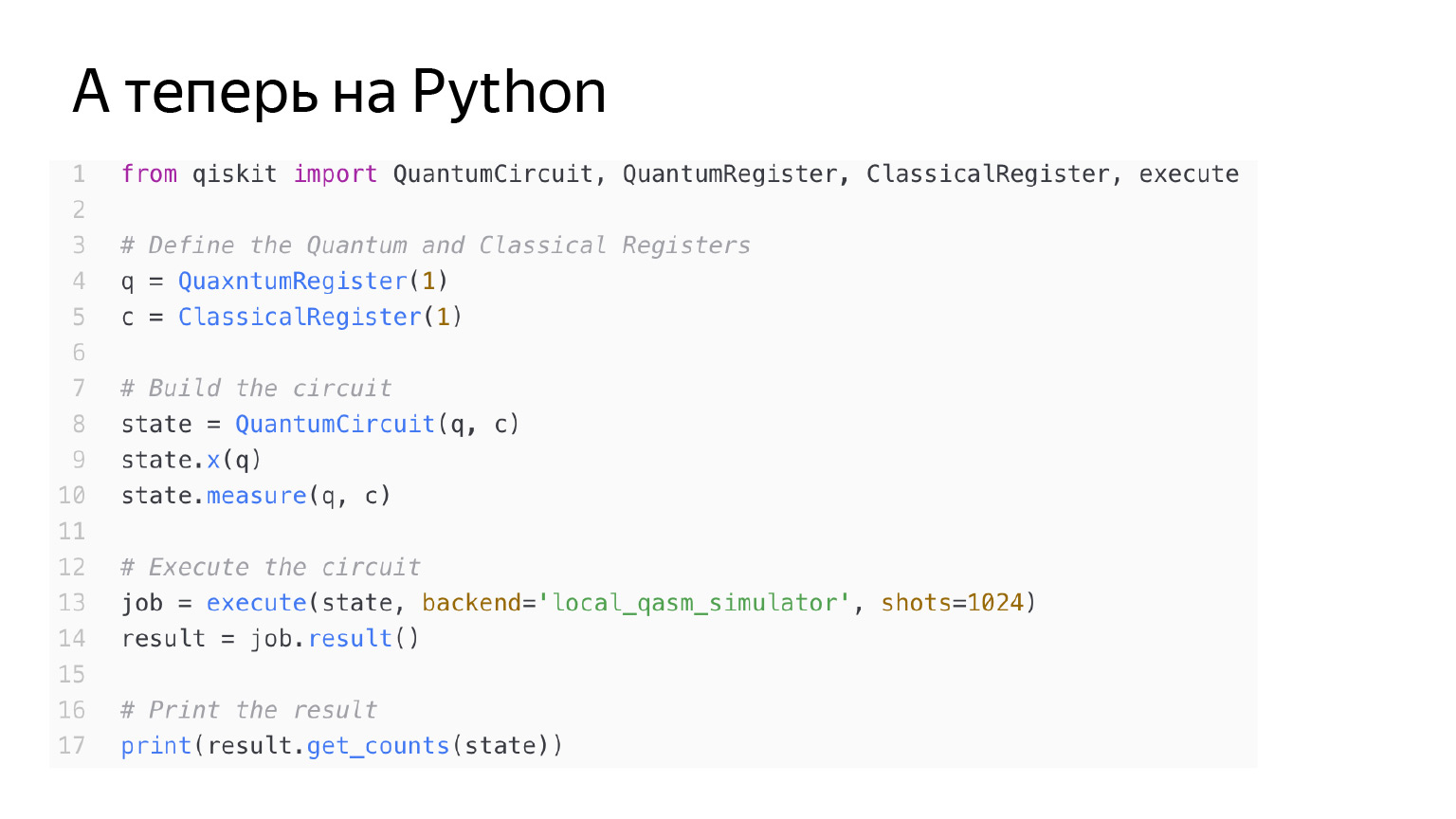
Код такой же. Просто здесь я еще применяю оператор X к кубиту q.

Хорошо, попробуем пойти дальше.

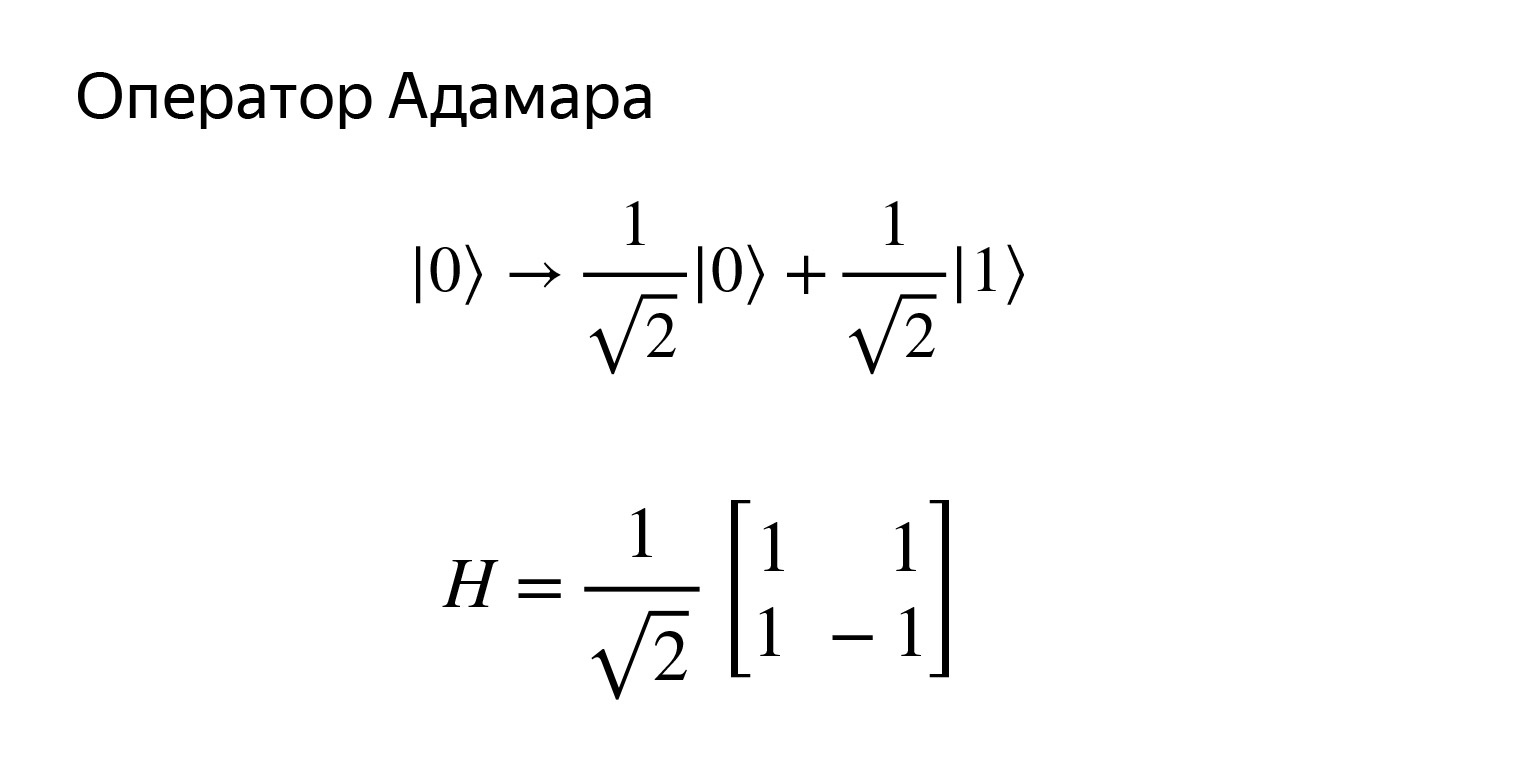
Здесь есть очень хитрая штука. Попробуем получить вот такое состояние. Это состояние очень интересное. Мы получим такую суперпозицию. Если мы попробуем ее измерить, то с вероятностью ½ получим или нолик, или единичку. То есть это будет такая равномерная суперпозиция, можем получить что угодно.

Можно провести аналогию, что это такое квантовое подбрасывание монетки. Мы скажем, что окей, с вероятностью ½ получим нолик и единичку. Матричка выглядит вот так.

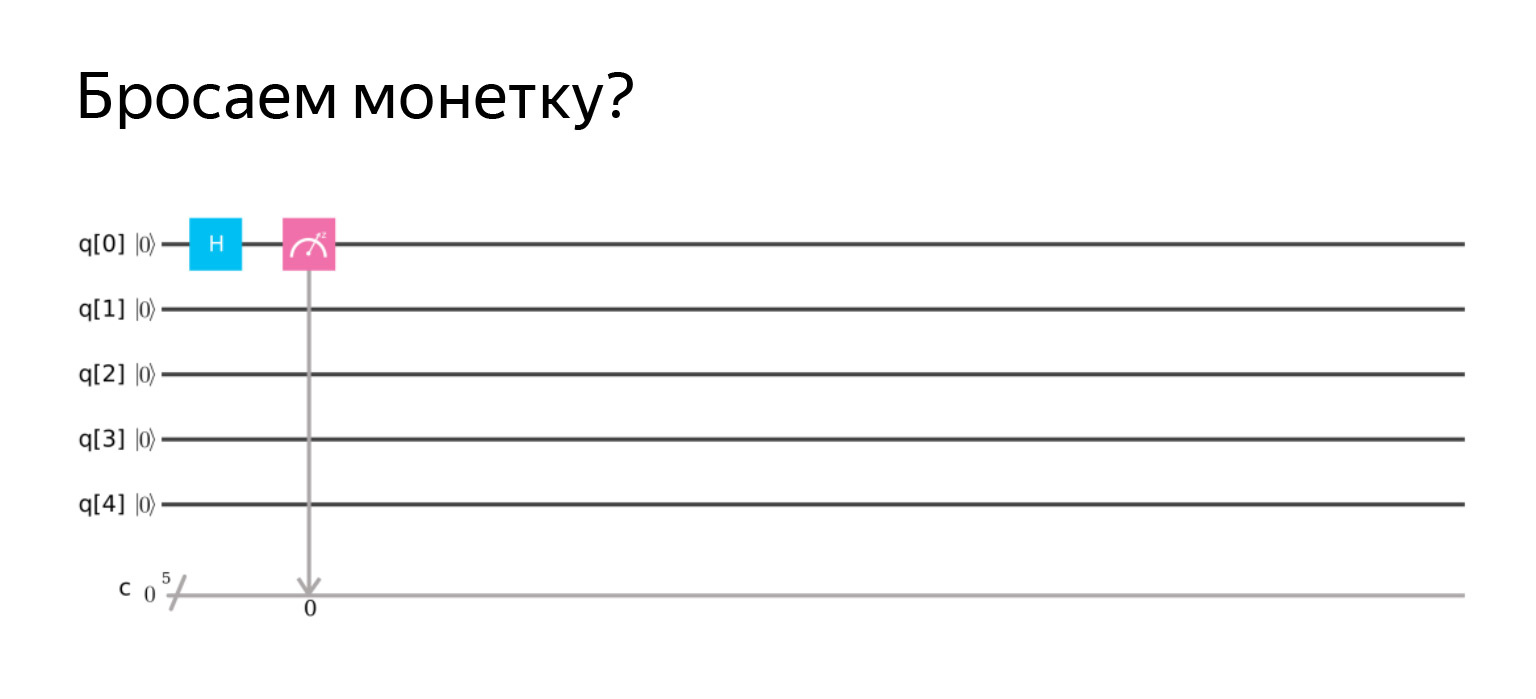
Легко проверить, но мы, конечно, не будем. Нарисуем схему. Оператор H в честь Адамара.

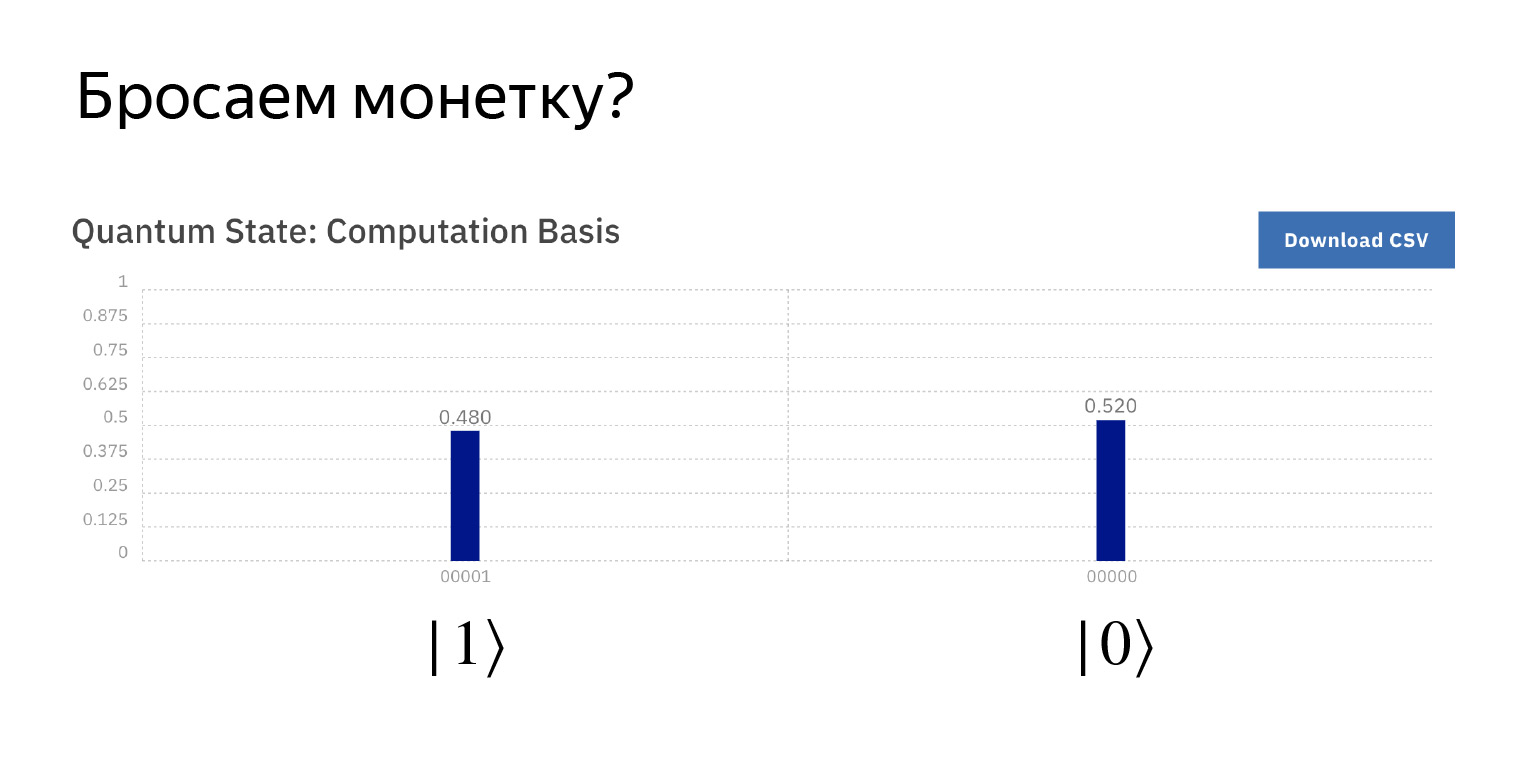
Замерим и получим примерно то, что ожидаем. Примерно с вероятностью ½, нолик и единичка. Чуть больше, чуть меньше, но так уж получается.

Вот код на Python, просто чтобы был, мы же на конференции про Python.

Есть такая суперпозиция. К ней применяем оператор Адамара и замеряем.

Но монетку можно бросить два раза, к этому мы все привыкли. Если бросить монетку два раза, ничего не поменяется. Давайте попробуем это сделать в квантовом случае.

Два раза подряд применим оператора Адамара и всегда получим нолик.

То есть если квантовую монетку бросить два раза, то всегда получится нолик, потому что оператор Адамара обратный сам к себе. Если вы умножите самого на себя, всегда получите единичку. Вот такая штука.

Итак, с одним кубитом можно что-то делать. Можно крутить, вертеть и измерять. Давайте попробуем добавить побольше кубит. Что мы привыкли делать в классическом мире? Брать и выполнять простые логические операции, «или» и «и».

В квантовом мире так делать нельзя, потому что они не совсем обратимые. То есть, получая ноль в операции «и», мы никогда не сможем узнать, какие были начальные значения.

А в квантовом мире, как я говорил, операция — это унитарные матрицы, которые всегда обратимы. Как тогда вообще программировать? Все, к чему мы привыкли, рушится. Но появляется новый герой, это оператор так называемого контролируемого отрицания.

Если бы мы писали на Python, это выглядело бы так. Если в первом кубите единичка, давайте инвертировать второй кубит. Это не матричка, это то, как выглядит оператор. Но в принципе то, что я сказал, тут и написано. Там, где в первом кубите единичка, второй инвертируется.

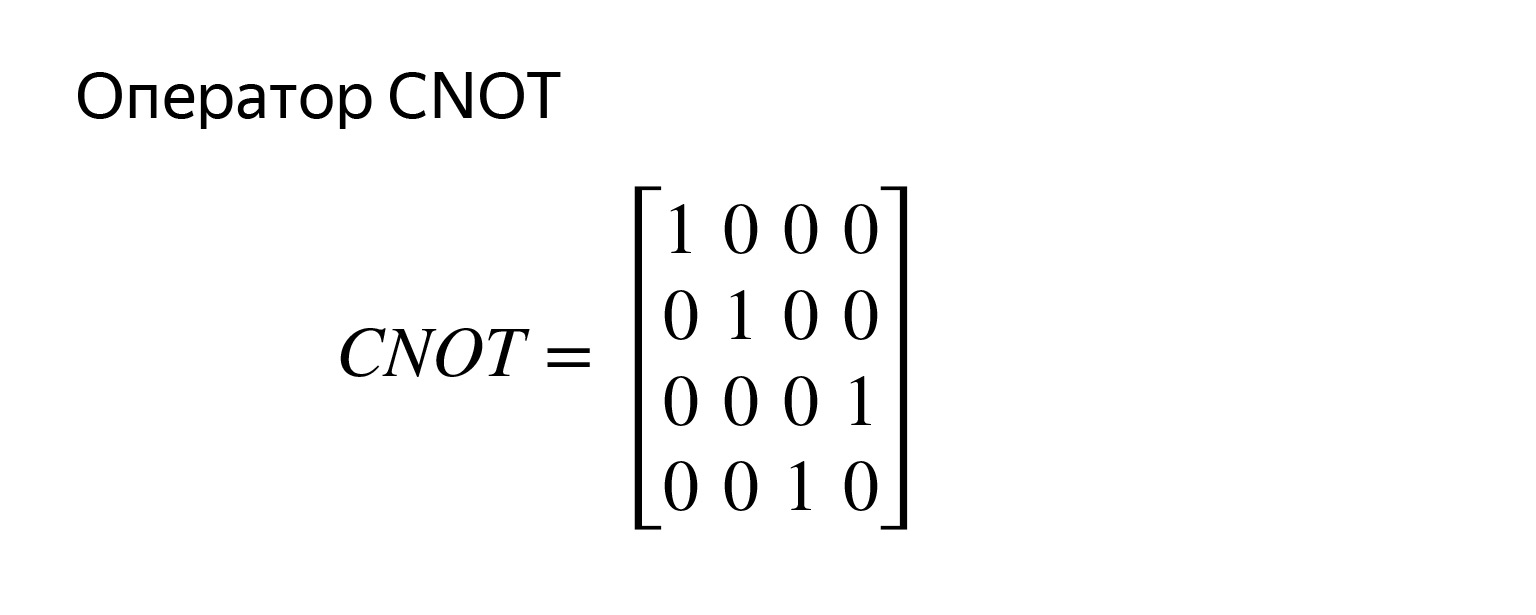
Матричка уже четыре на четыре. Для двух кубит она выглядит так. Оставлю задачу со звездочкой, чтобы перемножить и посмотреть, что это правда так.

Эту штуку можно даже запрограммировать. Никакого rocket science. Нужно просто взять, создать схему с двумя кубитами, с двумя классическими, и сделать, только не CNOT, а CX, контролируемое отрицание.

Отрицание было оператором X, поэтому в принципе все логично. И можно нарисовать схему. Схема такая.

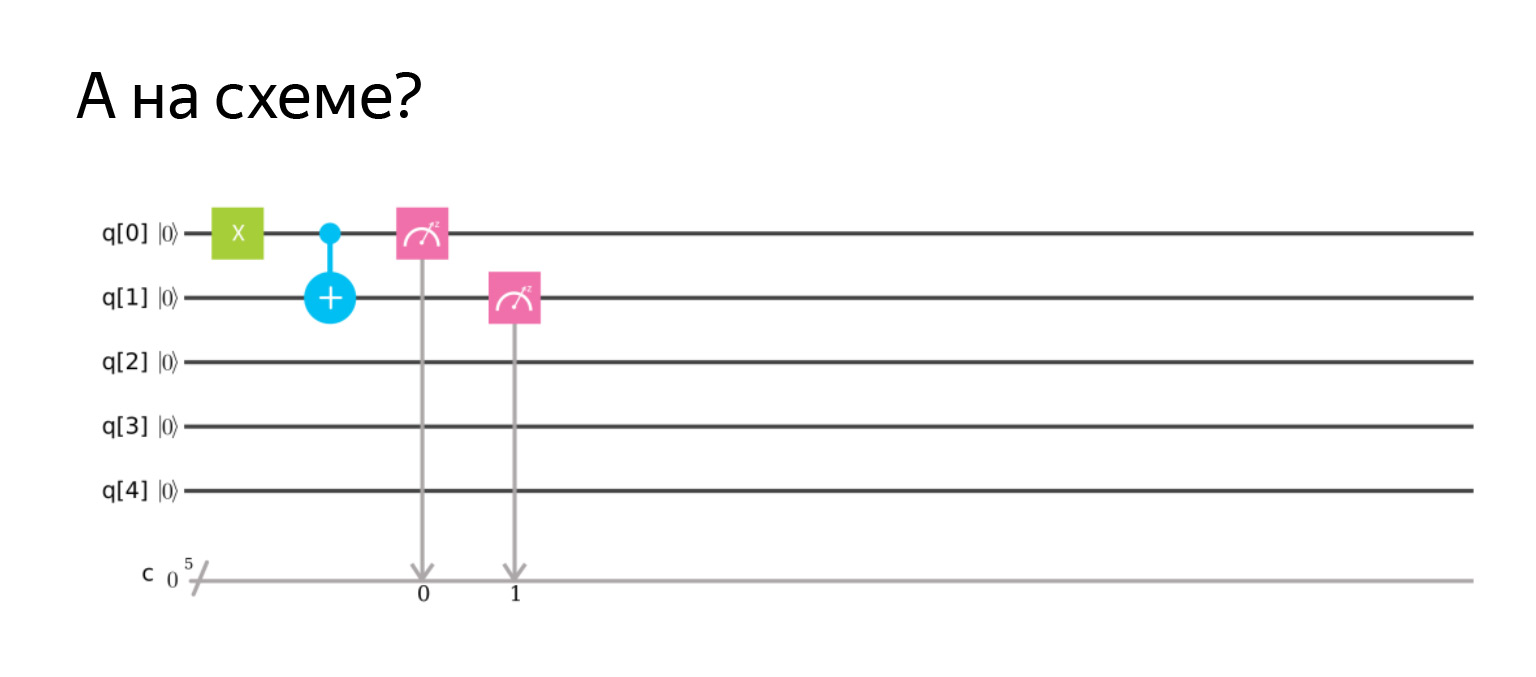
То есть контролируемое отрицание — это такой плюсик на кубите, который мы хотим менять. И точечка, которая является контрольной. Здесь, если кубит в единичке, то второй будем менять.

Тут я специально первый сначала инвертирую, чтобы он был единичкой, и потом замеряю оба и получаю результат |11⟩. Все как мы и предполагали.

Но теперь самое время использовать все наши знания вместе.

Возьмем и все три или четыре оператора, которые мы знаем, залепим в одну схему. То есть мы к первому оператору применим оператор Адамара. Второй инвертируем, потом все вместе, сделаем контролируемое отрицание и измерим.

Давайте не будем пока запускать, а попробуем угадать, что же получится.

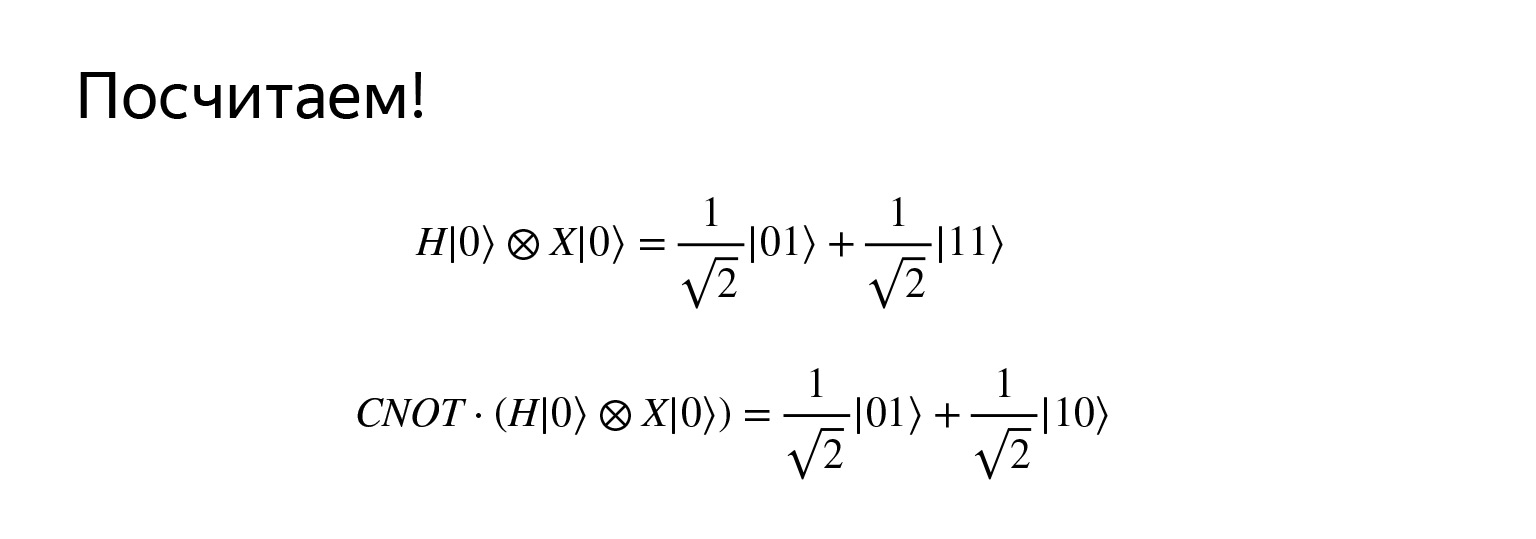
Если мы к первому кубиту применяем оператора Адамара, а ко второму отрицание, то получим такую суперпозицию. Я не хочу сейчас тратить время на проверку, это можно легко перемножить. Но позиция очень интересная. Во-первых, она очень похожа на равномерную, а, во-вторых, теперь это состояние называется запутанным, если еще взять контролируемое отрицание.

Состояние запутанное. А все почему? Попробуем произвести измерение. Смотрите, если я измеряю первый кубит и он у меня в состоянии ноль, я тогда могу сказать, что второй кубит обязательно в состоянии один.

То есть если я сделаю такое преобразование своими кубитами, один кубит отдам своему другу, он улетит в Нью-Йорк, а я второй кубит измерю у себя, я буду точно знать, в каком состоянии его кубит. Это называется эффектом квантовой запутанности или квантовой связанности. И это основной механизм, с помощью которого квантовые вычисления работают. Он изменится, они связаны очень жестко, и во время измерения мы можем получить только |00⟩ или |11⟩.

По этому поводу есть очень интересная иллюстрация в пользу одного ученого, австрийского, по-моему, который был очень рассеянным.

Рассеянность заключалась в том, что он все время носил разные носки. И коллеги над ним шутили: если он заходит в комнату одной ногой и мы видим, что носок розовый, то можем точно сказать, что второй носок не розовый. Такие дела.

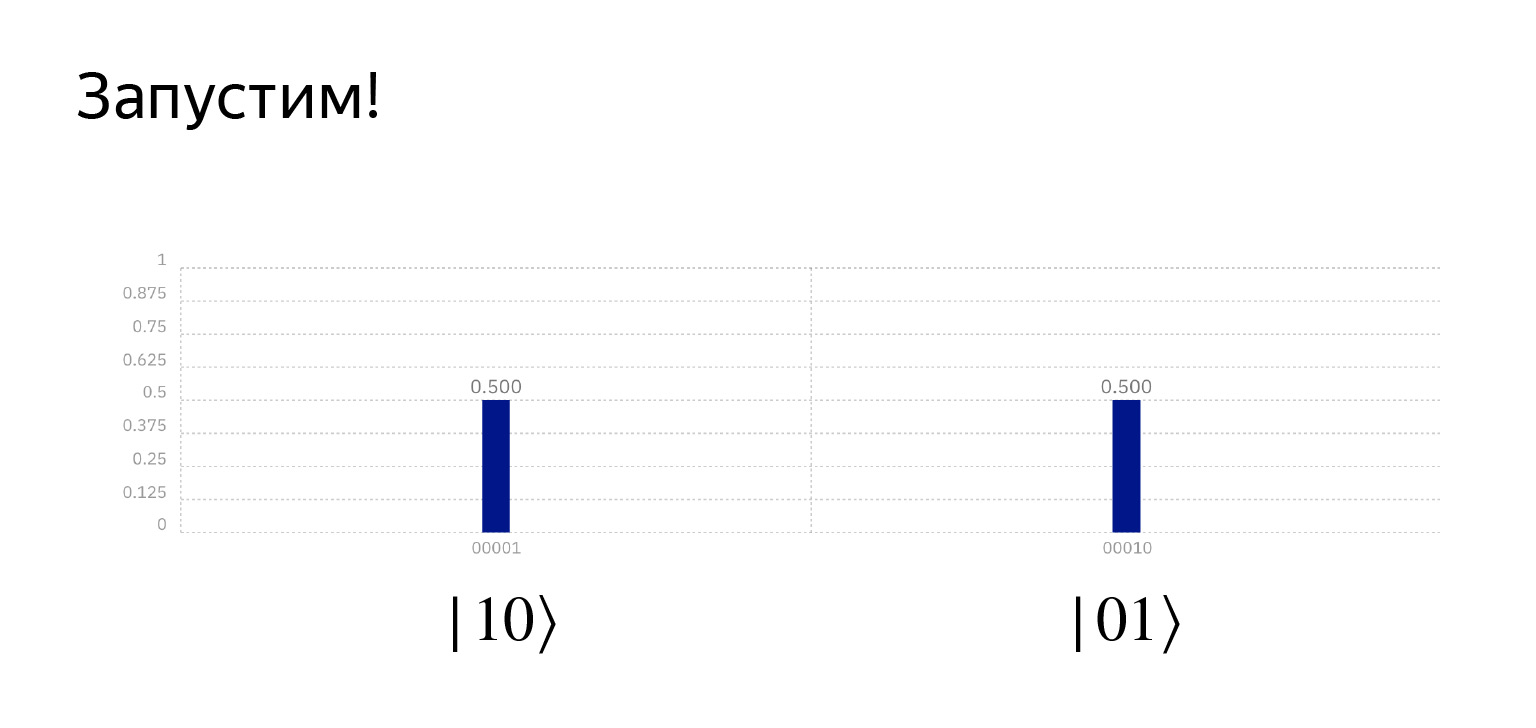
Если мы эту штуку запустим, получим ровно то, что хотим. Здесь уже совсем смешно получилось. Вероятность ровно 0,5, но это совпадение.

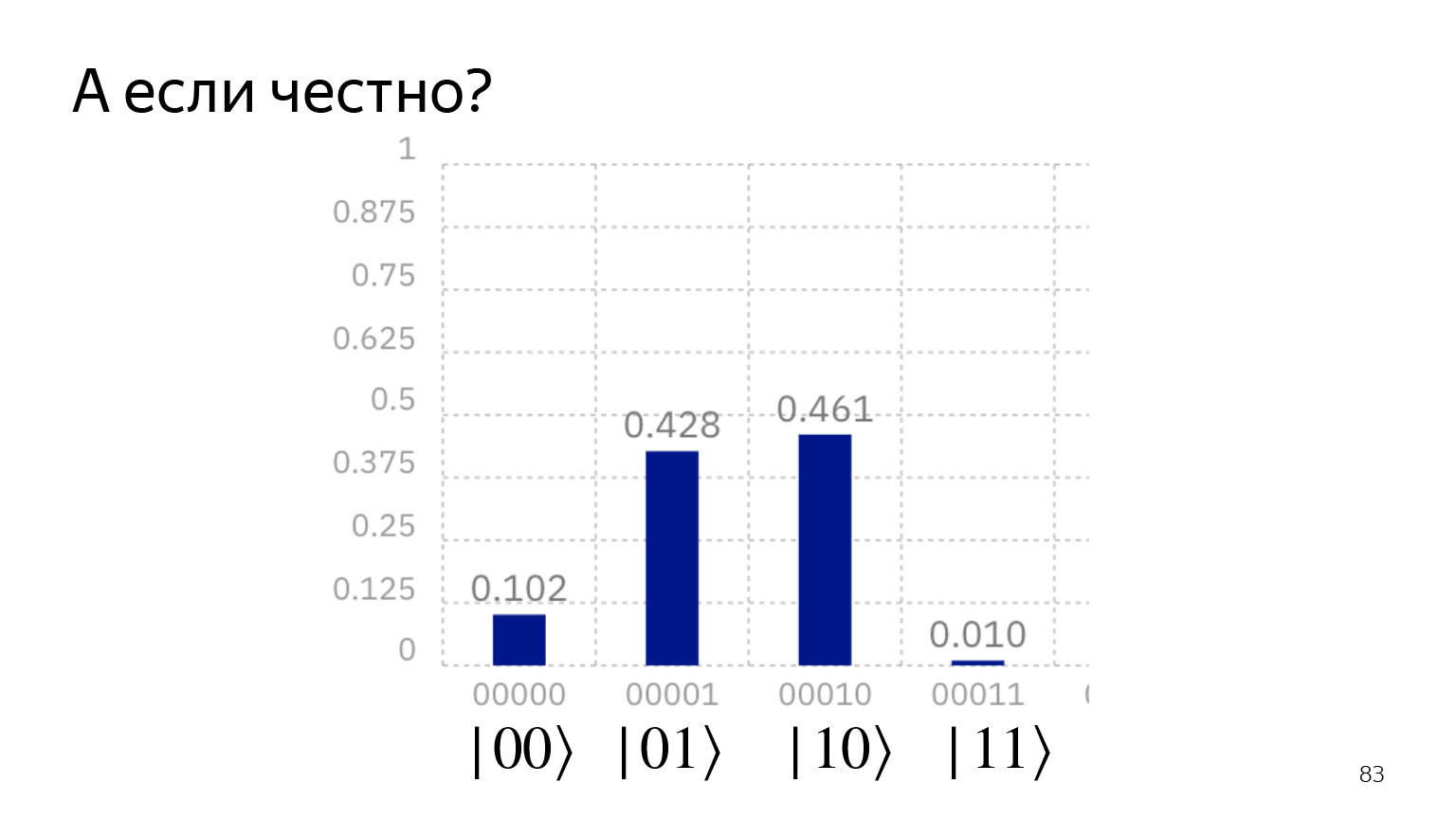
Если мы будем честно запускать на квантовом компьютере, получим вот такую картину. Вроде бы мы говорим: никогда не может получиться состояние |00⟩ и никогда не может получиться состояние |11⟩. Но оно все-таки получается: текущее состояние техники таково, что там есть шумы, которые не всегда можно легко подавить. И с этим борются.

Но если вы вспомните классическую информатику, там то же самое: коды, исправляющие ошибки и все такое. Просто кубит пока слишком мало, чтобы тратить дополнительные биты на исправление ошибок.

Теперь, как я и обещал, несколько примеров алгоритмов. Но это будут просто голословные примеры без разборов алгоритмов, чтобы вы посмотрели, подумали, заинтересовались.

Первый алгоритм как раз связан с Дойчем, о котором мы говорили вначале. Это алгоритм Дойча-Йожи. И он делает следующее. Представьте, что у нас есть булева функция от n переменных. И мы точно знаем, что она или константная, или сбалансированная. Сбалансированная — значит, ровно на половине аргументов она равна нулю, а на другой половине — единичке. Попробуем классически проверить, константна она или нет.

Для этого нам нужно проверить хотя бы половину всех возможных вариантов: 2n–1+1 вариант. Квантовый алгоритм позволяет это сделать за n обращений к самой функции, за n вычислений самой функции. Это экспоненциально меньшее количество обращений.

Второй пример, наверное, хорошо всем известен, из-за него говорят, что квантовые компьютеры сломают всю криптографию: мы можем квантово очень быстро факторизовать числа.

Здесь приведены оценки сложности, и есть просто фантастический пример. В 2011 году на реальном компьютере факторизовали число 15. Потребовалось семь кубит.

Но не все так страшно. На случай, если квантовые компьютеры достигнут уровня, при котором можно ломать RSA, уже есть постквантовая криптография. Она построена на обучении с ошибками. Это когда в задачи вносится небольшая погрешность так, чтобы найти ответ было очень сложно. Обычно это какие-то уравнения или система уравнений. Вот пример алгоритма. Кто захочет, может почитать подробнее.

Самое интересное: на этой штуке основан алгоритм New Hope, новая надежда всея человечества. В 2016 году в Chrome была включена поддержка этого алгоритма. Здесь есть ссылочка на блог. Это не я придумал, все на самом деле есть. Будущее уже здесь.

В конце немножко ссылок:

На этом более-менее все. Я хочу только добавить, что примерно 50 лет назад, когда Дойч начал заниматься квантовой информатикой, компьютеры были большие. Их делало несколько компаний. Они были размером со шкаф. А сейчас примерно те же компании делают большие квантовые компьютеры. И что будет через 50 лет мы, конечно, не знаем.

Если вы попробуете вбить в своем любимом поисковике, то уже сегодня можете найти вакансии для квантового программиста. Конечно, там больше исследований, но тем не менее. Спасибо.

© Habrahabr.ru