Triton vs Kao’s Toy Project. Продолжаем хорошую традицию

В данной статье речь пойдет про SMT-решатели. Так сложилось, что в исследовательских материалах, посвященных данной теме, появилась хорошая традиция. Уже несколько раз в качестве подопытного алгоритма для SMT-решателей разные исследователи выбирали один и тот же пример — крякми, придуманное некогда человеком с ником kao. Что ж, продолжим эту традицию и попробуем использовать для решения этого крякми еще один инструмент для символьных вычислений — Triton.
Пара слов про SMT-решатели
Задача выполнимости формул в теориях (англ. satisfiability modulo theories, SMT) — это задача выполнимости для логических формул с учётом лежащих в их основе теорий. Примерами таких теорий для SMT-формул являются: теории целых и вещественных чисел, теории списков, массивов, битовых векторов и т. п. — wikipedia
Задача SMT является расширением задачи SAT (Boolean satisfiability problem или Propositional Satisfiability Problem, в англоязычной литературе называется SATISFIABILITY или SAT, в русской литературе иногда называется ВЫП).
Еще одна цитата из Википедии:
Экземпляром задачи SAT является булева формула, состоящая только из имен переменных, скобок и операций И, ИЛИ и HE. Задача заключается в следующем: можно ли назначить всем переменным, встречающимся в формуле, значения «ложь» и «истина» так, чтобы формула стала истинной. — wikipedia
Поскольку SMT-решатели работают с различными теориями, становится возможным их применение для алгоритмов в традиционных процессорных архитектурах. Таким образом, SMT-решатели позволяют решить две задачи:
- ответить на вопрос, возможны ли данные выходные значения алгоритма при данных входных значениях;
- определить, при каких входных значениях результатом алгоритма будут данные выходные значения.
SMT-решатели имеют прикладные применения в различных областях науки и техники. Существуют отдельные инструменты для решения формул SMT, например, Z3, miniSAT, CVC4 и др., и для представления алгоритмов на машинном языке в синтаксисе формулы SMT, например, BAP, radare2 или angr. Инструменты постоянно совершенствуются, API становится мощнее, и теперь достаточно буквально нескольких кликов для применения всего математического аппарата SMT в задачах реверс-инжиниринга.
Отметим также, что существует несколько видов символьного исполнения. Статическое символьное исполнение (SSE, Static symbolic execution) основывается только на символьных переменных и использует только символьные формулы. Динамическое символьное исполнение (DSE, Dynamic symbolic execution), также называемое concolic execution, использует символьные вычисления наряду с конкретными значениями численных переменных в ходе выполнения программы. В данной работе мы будем использовать только статическое символьное исполнение.
История крякми Kao’s Toy Project
Крякми Kao«s Toy Project устроено предельно просто. В одном окне оно выводит некоторую шестнадцатеричную последовательность и предлагает ввести ключ, валидный для данной последовательности.
Его историю можно представить в виде следующей хроники:
04.03.2012 — Kao«s Toy Project and Algebraic Cryptanalysis — dcoder, andrewl — алгебраический криптоанализ, SAT
Первая работа, посвященная этому крякми, появилась в 2012 году. В ней человек с ником dcoder опубликовал решение с помощью алгебраического криптоанализа, а соавтор этой работы andrewl успешно применил SAT-решатель.
06.03.2012 — Semi-Automated Input Crafting by Symbolic Execution, with an Application to Automatic Key Generator Generation — Rolf Rolles — z3, самописный конвертер
Потом известный исследователь Rolf Rolles впервые применил для решения SMT-решатель. Сначала он вручную составил формулу на языке Z3, а потом представил на языке OCaml инструмент для автоматической генерации формулы из промежуточного представления машинного кода. Промежуточный язык, который он использовал, был разработан им самим.
I use an IR very similar to the one used by BitBlaze and BAP, but I wrote my own IR translator rather than using VEX. My implementation is written-from-scratch and shares no code with the open-source frameworks. — openrce.org
11.2013 — SMT Solvers for Software Security — Георгий Носенко — BAP, z3
Потом появилась работа моего коллеги Георгия Носенко, где для генерации формулы уже использовался фреймворк BAP и тот же решатель Z3.
03.2015 — Automated algebraic cryptanalysis with OpenREIL and Z3 — Cr4sh — OpenREIL, z3
Дмитрий Олексюк, также известный как Cr4sh, в своем исследовании использовал конвертацию в промежуточный язык OpenREIL с последующей генерацией формулы в Z3.
04.2016 — Solving kao’s toy project with symbolic execution and angr — Extreme Coders Blog — angr
И, наконец, еще одна работа появилась в 2016 году, и в ней описывается решение с использованием фреймворка angr. Angr применяет промежуточный язык VEX и библиотеку claripy для символьного исполнения.
На арене SMT теперь появился еще один игрок — Triton, и мы в данной работе воспользуемся им, чтобы решить знаменитое крякми.
Triton
Triton создан компанией Quarkslab, создавшей немало интересных инструментов для реверс-инжиниринга.
Сначала немного о том, как устроен Triton. В ходе своей работы он выполняет следующие действия:
- парсит трассу выполнения бинарного кода и генерирует абстрактное синтаксическое дерево кода с учетом всех побочных эффектов машинных инструкций;
- обходит абстрактное синтаксическое дерево и генерирует формулу SMT в формате SMT-LIB;
- решает формулу с помощью решателя z3.
При построении абстрактного синтаксического дерева Triton не использует промежуточного представления машинного кода (в отличие от bap или angr), и на данный момент поддерживает только работу с архитектурами x86 и x86–64.
Triton может работать в одном из двух режимов. В первом — online mode — трасса выполнения записывается с помощью специального трассировщика, который входит в состав Triton и использует DBI-фреймворк pin. Во втором — offline mode — трасса записывается внешними средствами. Трасса должна содержать последовательность инструкций и их опкоды. Во втором случае уже необходимо самостоятельно создать начальный контекст, то есть определить значения регистров и используемую память.
API, который предоставляет Triton, очень богатый и … очень нестабильный. С момента появления API менялся уже раза четыре, конечно, не сохраняя обратную совместимость. Из-за этого код старых инструментов, использующих Triton, для запуска на новых версиях надо переписывать. Приятным моментом является то, что API имеет binding«и для Python. В репозитории есть несколько примеров, демонстрирующих использование API на С++ и на Python, благодаря которым с ним довольно несложно разобраться.
Итак, приступим к решению.
Решение
Сначала нам надо найти алгоритм, по которому выполняется проверка введенного ключа. Бегло пробежав по коду, видим, что генерируемая последовательность представляет собой на самом деле восемь 32-разрядных целых чисел, и лежит в памяти последовательно в представлении little-endian, в то время как в окне показывается как big-endian. Узнаем, что ключ имеет формат XXXXXXXX-XXXXXXXX, где X — шестнадцатеричный разряд. Если ключ введен в таком формате, происходит вызов процедуры проверки. Так она выглядит в дизассемблере IDA Pro.
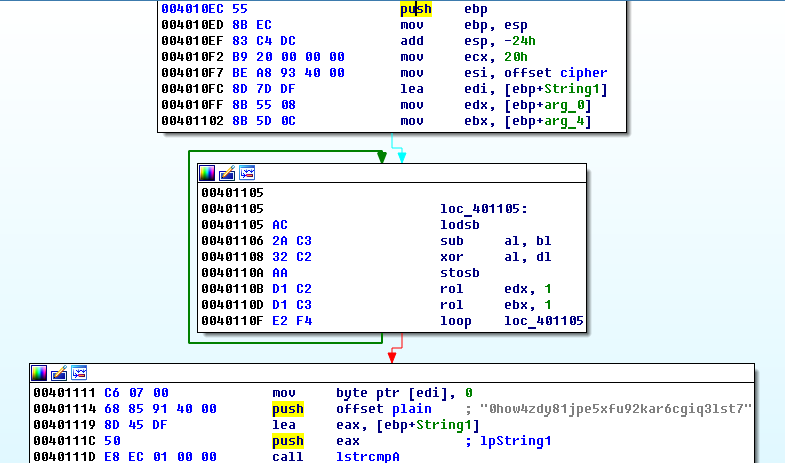
В процедуре проверки сначала происходит инициализация входных данных: cipher — 32-байтовая исходная последовательность в представлении little-endian, String1 — буфер для выходной последовательности после преобразования, в регистрах edx и ebx находятся две половинки ключа, представленные как 32-разрядные целые числа. Далее идет сам алгоритм преобразования — 32 цикла с операциями xor и rol — и затем полученная строка из буфера String1 сравнивается со строкой »0how4zdy81jpe5xfu92kar6cgiq3lst7». Если они идентичны, ключ считается верным.
Таким образом, формируется следующая задача для SMT-решателя: определить, на каких входных значениях регистров edx и ebx заданная шестнадцатеричная последовательность после выполнения алгоритма преобразуется в строку »0how4zdy81jpe5xfu92kar6cgiq3lst7».
Поскольку крякми написано для Windows, трассировщик Triton не подойдет, ведь он поставляется только скомпилированным для Linux. Можно, конечно, попытаться скомпилировать его самостоятельно для Windows, но это те еще приключения. Поэтому мы будем использовать режим offline и байндинги Triton«а для Python.
Сначала введем необходимые константы:
ADDR_CIPHER = 0x4093A8
ADDR_TEXT = 0x409185
ADDR_EBP = 0x18f980
TEXT = "0how4zdy81jpe5xfu92kar6cgiq3lst7"
cipher = Noneи произведем начальную инициализацию:
ctx = TritonContext()
ctx.setArchitecture(ARCH.X86)
ctx.setConcreteRegisterValue(ctx.registers.ebp, ADDR_EBP)
ctx.setConcreteRegisterValue(ctx.registers.esp, 0x18f95b)
ctx.setConcreteRegisterValue(ctx.registers.eip, 0x4010ec)
ctx.setConcreteMemoryAreaValue(ADDR_CIPHER, cipher)
ctx.setConcreteMemoryAreaValue(ADDR_TEXT, list(map(ord, TEXT)))
edx = ctx.convertRegisterToSymbolicVariable(ctx.getRegister(REG.X86.EDX))
ebx = ctx.convertRegisterToSymbolicVariable(ctx.getRegister(REG.X86.EBX))
keys = [ctx.convertMemoryToSymbolicVariable(MemoryAccess(ADDR_EBP-0x21, 1)) for i in xrange(32)]Во время инициализации мы создаем контекст, устанавливаем архитектуру, инициализируем регистры и память и, конечно, создаем символьные переменные: регистры edx и ebx и буфер для преобразованной последовательности, на значения которого будут наложены ограничения в формуле.
Теперь создаем трассу выполнения. Для этого в режиме offline достаточно загрузить бинарный код:
code = {0x4010EC: '\x55', # push ebp
0x4010ED: '\x8b\xec', # mov ebp, esp
0x4010EF: '\x83\xc4\xdc', # add esp, -24h
0x4010F2: '\xb9\x20\x00\x00\x00', # mov ecx, 20h
0x4010F7: '\xbe\xa8\x93\x40\x00', # mov esi, offset cipher
0x4010FC: '\x8d\x7d\xdf', # lea edi, [ebp+string1]
0x4010FF: '\x8b\x55\x08', # mov edx, [ebp+arg_0]
0x401102: '\x8b\x5d\x0c', # mov ebx, [ebp+arg_4]
# loc_401105:
0x401105: '\xac', # lodsb
0x401106: '\x2a\xc3', # sub al, bl
0x401108: '\x32\xc2', # xor al, dl
0x40110A: '\xaa', # stosb
0x40110B: '\xd1\xc2', # rol edx, 1
0x40110D: '\xd1\xc3', # rol ebx, 1
0x40110F: '\xe2\xf4'} # loop loc_401105и запустить процессинг инструкций:
ip = 0x4010ec
while ip < 0x401111:
inst = Instruction()
inst.setOpcode(code[ip])
inst.setAddress(ip)
ctx.processing(inst)
ip = ctx.buildSymbolicRegister(ctx.registers.eip).evaluate()Во время процессинга инструкций Triton переводит их в символьную форму и добавляет полученные символьные инструкции в контекст. В данном коде мы еще используем символьную эмуляцию регистра ip, чтобы вычислить следующую инструкцию по порядку выполнения.
После этого осталось ввести в контекст необходимые ограничения на значения переменных. У нас это условие равенства преобразованной строки со строкой »0how4zdy81jpe5xfu92kar6cgiq3lst7», которую мы поместили в константу TEXT.
for i in xrange(32):
r_ast = ast.bv(ord(TEXT[i]), 8)
l_id = ctx.getSymbolicMemoryId(ADDR_EBP-0x21 + i)
l_ast = ctx.getAstFromId(l_id)
ex = ast.equal(l_ast, r_ast)
expr.append(ex)
expr = ast.land(expr)Ограничения задаются в виде узлов абстрактного синтаксического дерева (АСД). У нас в цикле создается узел АСД для одного символа из строки и узел АСД для одного элемента преобразованной последовательности. Затем создается новый узел АСД с операцией сравнения этих двух узлов. Так как нам надо, чтобы условия равенства всех элементов выполнялись одновременно, после получения их в цикле они объединяются в одно АСД под операцией логического «И» expr = ast.land (expr).
Все готово для вычисления решения. Получаем модель данных для символьной формулы с заданными ограничениями expr.
model = ctx.getModel(expr)Весь скрипт кейгена целиком можно скачать отсюда.
Запускаем скрипт и … ничего не происходит. Отладка показывает, что выполнение зацикливается на этапе процессинга инструкций, и быстро становится понятно, что не выполняется обработка инструкции loop. Оказывается, Triton даже не знает эту инструкцию. Как справиться с этой проблемой? Можно добавить семантику новой инструкции в исходники Triton и пересобрать его. Но мы уже отмечали, что пересборка на Windows — довольно кропотливое дело. Хм, ну ладно, не будем сразу расстраиваться, и попытаемся переделать наш код. Можно попробовать заменить loop на такой же по действию набор инструкций, например:
dec ecx
jz 0401105hА можно попробовать развернуть цикл вручную, и сделать процессинг не блока с циклом внутри, а только тела цикла столько раз, сколько записано в регистре ecx, то есть 32. Тогда код будет выглядеть так:
code = ['\xac', # lodsb
'\x2a\xc3', # sub al, bl
'\x32\xc2', # xor al, dl
'\xaa', # stosb
'\xd1\xc2', # rol edx, 1
'\xd1\xc3'] # rol ebx, 1
ctx.setConcreteRegisterValue(ctx.registers.esi, ADDR_CIPHER)
ctx.setConcreteRegisterValue(ctx.registers.edi, ADDR_EBP - 0x21)
ctx.setConcreteRegisterValue(ctx.registers.eip, 0x401105)
ctx.setConcreteMemoryAreaValue(ADDR_CIPHER, cipher)
ctx.setConcreteMemoryAreaValue(ADDR_TEXT, list(map(ord, TEXT)))
edx = ctx.convertRegisterToSymbolicVariable(ctx.registers.edx)
ebx = ctx.convertRegisterToSymbolicVariable(ctx.registers.ebx)
ip = 0x401105
for i in xrange(32):
for c in code:
inst = Instruction()
inst.setOpcode(c)
inst.setAddress(ip)
ctx.processing(inst)
ip = ctx.buildSymbolicRegister(ctx.registers.eip).evaluate()Итак, запускаем новый вариант. На этот раз процессинг выполняется целиком и успешно доходит до вычисления модели, в которое она погружается, ожидаемо, на некоторое время. Ждем… ждем… уже очень долго ждем. Я так и не дождался. На этот раз, проблема в функции вычисления модели, и тут ошибку может быть не так просто обнаружить. Можно предположить, что получившаяся формула очень большая, и ее вычисление действительно может занимать очень много времени. Чтобы проверить это, сократим число итераций в цикле, где происходит процессинг. Действительно, при меньшем числе итераций, результат выдается. Методом подбора было обнаружено, что верхняя граница числа итераций, при котором вычисления занимают обозримое время, на опытном ноутбуке это 12. Да, это очень мало, и с их увеличением время растет экспоненциально. 32 итерации — это намного больше 12, и, кажется, даже если переписать код на С++, все равно вычисление модели будет неприемлемо долгим.
Если попробовать посмотреть в отладке, что же в функции getModel занимает так много времени, мы увидим, что это рекурсивные вызовы функции triton::ast::TritonToZ3Ast::convert.
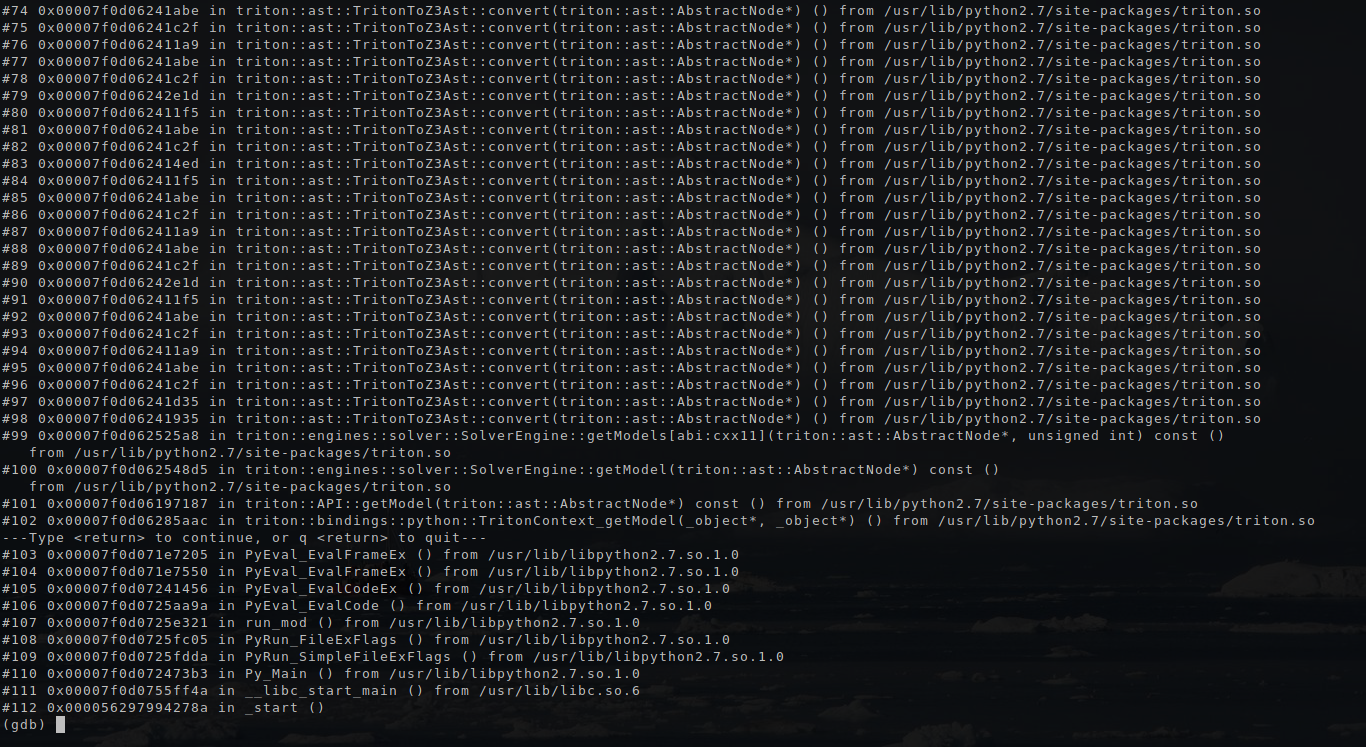
Как написано в документации, Triton использует свое кастомное дерево АСД:
An abstract syntax tree (AST) is a representation of a grammar as tree. Triton uses a custom AST for its expressions. As all expressions are built at runtime, an AST is available at each program point. — Triton documentation
Данная функция конвертирует АСД Triton«а в выражение для z3.
Можно попробовать посмотреть на выражения, которые составляют АСД Triton«а. Добавим перед получением модели следующие строки:
tsym = ctx.getSymbolicExpressions()
for ek in sorted(tsym.keys()):
e = tsym[ek].getAst()
print str(e)После этого в консоли появятся выражения Triton«а такого вида:
ref!0 = SymVar_0
ref!1 = SymVar_1
ref!2 = SymVar_33 ; Byte reference
ref!3 = (concat ((_ extract 31 8) (_ bv0 32)) (_ bv29 8)) ; LODSB operation
ref!4 = (ite (= (_ bv0 1) (_ bv0 1)) (bvadd (_ bv4232104 32) (_ bv1 32)) (bvsub (_ bv4232104 32) (_ bv1 32))) ; Index operation
ref!5 = (_ bv4198662 32) ; Program Counter
ref!6 = (concat ((_ extract 31 8) ref!3) (bvsub ((_ extract 7 0) ref!3) ((_ extract 7 0) ref!1))) ; SUB operation
ref!7 = (ite (= (_ bv16 8) (bvand (_ bv16 8) (bvxor ((_ extract 7
…Чтобы получить выражения в синтаксисе SMT-LIB, надо добавить еще один вызов.
print ctx.unrollAst(e)В этом месте — unrollAst — происходит та же конвертация выражений Triton«а в выражения SMT-LIB, и здесь вы также не дождетесь завершения, как и с функцией getModel.
Знакомые с синтаксисом SMT-LIB заметят, что выражения Triton«а представляют собой выражения SMT-LIB, только в форме SSA (Single Static Assignment). В SMT-LIB нет операции присваивания переменных — их заменяет функциональный оператор let. А что, если попробовать самостоятельно сконвертировать синтаксис Triton«а в синтаксис SMT-LIB без разворачивания АСД, а заменяя форму SSA на форму с операторами let, и потом попытаться скормить это z3py? Звучит довольно громоздко и избыточно, но выходить из сложившегося положения надо, пока разработчики не допилили Triton.
Итак, с получившимся выражением мы проводим следующие действия:
- Объявляем переменные в синтаксисе SMT-LIB;
- Заменяем операторы присваивания на операторы let;
- Получившиеся выражения соединяем в общую формулу на языке SMT-LIB.
В результате получается функция конвертации из синтаксиса Triton в синтаксис SMT-LIB. Она, конечно, не универсальна, но, по-крайней мере, для нашей задачи работает.
def convert(ctx, asserts):
zsym = ""
tsym = ctx.getSymbolicExpressions()
for ek in sorted(tsym.keys()):
e = tsym[ek].getAst()
if e.getKind() == AST_NODE.VARIABLE:
zsym += "(declare-fun ref!%d () (_ BitVec %d))\n" % (ek, e.getBitvectorSize())
nodes = []
for ek in sorted(tsym.keys()):
e = tsym[ek].getAst()
if e.getKind() <> AST_NODE.VARIABLE:
nodes.append("let ((ref!%d %s))" % (ek, e))
# print reduce(lambda x, y: "%s (%s)" % (x, y), reversed(nodes))
def fold(x, y):
if not isinstance(y, list):
raise TypeError
if len(y) == 1:
return y[0]
return "%s\n(%s)" % (x, fold(y[0], y[1:]))
nodes = ["assert"] + nodes
nodes[-1] += '\n' + str(asserts)
zsym = zsym + '(' + fold(nodes[0], nodes[1:]) + ')'
return zsymРезультат функции необходимо отправить на вычисление решателю z3py.
s = z3.Solver()
cs = z3.parse_smt2_string(expr)
s.assert_exprs(cs)
s.check()
m = s.model()
edx, ebx = m.decls()Теперь в переменных edx и ebx хранятся объекты класса z3.z3.FuncDeclRef. Получаем их численное представление, и, поскольку преобразования в крякми выполняются после того, как они поксорились друг с другом, необходимо их также поксорить.
edx, ebx = m[edx].as_long(), m[ebx].as_long()
print "%x-%x" % (edx, edx ^ ebx)Код второй версии можно взять также с гитхаба.
Итак, мы получим строку, которую надо просто скопировать в поле ввода в окне крякми. Руки чешутся уже это сделать.

Ура! Наш кейген работает правильно.
Ponce
На основе Triton построен еще один классный инструмент — плагин Ponce для IDA Pro. Он позволяет делать очень заманчивые вещи — символьное исполнение и taint-анализ прямо в дизассемблере IDA. К сожалению, из-за наличия в нашем крякми инструкции loop, проверить Ponce на нем нельзя. Может быть все-таки есть желающие добавить loop в Triton? :) Или есть еще один вариант. Поскольку крякми kao поставляется с исходниками на ассемблере, можно заменить там loop на вышеупомянутый аналогичный набор инструкций. Тогда получится использовать Ponce и почувствовать его силу. Для заинтересованного читателя это будет классной задачей.
Выводы
Откровенно говоря, Triton с задачей не справился. Но давайте не будем слишком строгими: инструкцию loop легко добавить самостоятельно, а конвертацию формулы, судя по истории сборок, разработчики уже начали делать итеративной.
Современный реверс-инжиниринг и поиск уязвимостей в программном обеспечении без символьного исполнения отходит в прошлое. Это доказывают, например, автоматические системы по поиску уязвимостей и генерации эксплойтов, созданные в ходе конкурса DARPA Cyber Grand Challenge. Поэтому такие инструменты, как Triton, сейчас очень востребованы. Развиваясь, они становятся все более простыми в использовании, так что символьное исполнение становится очень доступным и эффективным инструментом в работе исследователя.
