Тридцать шесть градусов красоты01.09.2018 17:33

Сеточные системы координат, в которых плоскость делится на одинаковые симметричные элементы — на квадраты, треугольники, шестиугольники, достаточно известны. Им соответствуют квадратная, треугольная, шестиугольная симметрия. Но еще существует симметрия десятиугольная.
В ней плоскость не делится на десятиугольники, вместо этого все линии расположены под углами кратными 36°. Координаты в этой системе можно записывать целыми числами, по два целых числа на горизонтальное и вертикальное направление.

Расскажу как это нарисовать.

Количество единичных векторов по всем направлениям в этой системе отсчета десять. Если учесть симметрию обратного направления, то пять. Если учесть горизонтальную симметрию, то три. Обозначим их как $(1,0), (x,y), (m,n)$ и выведем для них аналитические выражения.

Обычная формула расчета координат при повороте:
$\\x_a = \cos(a) x - \sin(a) y\\ y_a = \sin(a) x + \cos(a) y$

Двойной угол по этой формуле:
$\\m = x x - y y = x ^ 2 - y ^ 2 \\n = y x + x y = 2 x y$

Значит
$\\m = x ^ 2 - (1 - x ^ 2)\\ m = 2 x ^ 2 - 1$

И исходя из того что существует разница координат $d$
$\\m = x - d$
Получим квадратное уравнение
$\\2 x ^ 2 - 1 = x - d\\ 2 x ^ 2 - x - (1 - d) = 0$

Которое решается
$\\x = \left (1 \pm \sqrt{1 + 8(1 - d)}\right )/4$

Это говорит о том, что существует как положительное так и отрицательное значение координаты $x$ , при которых различие координат двойного и одинарного угла $d = x - m$ то же самое.

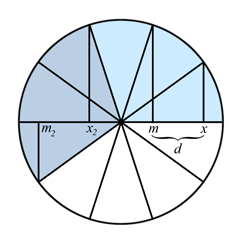
У десятиугольника такая симметрия, что разница горизонтальной координаты между одинарным и двойным углом при увеличении углов в три раза, то есть, между тройным углом и шестикратным, сохраняет точно такую же величину. Абсолютные значения координат m и x в парном решении меняются местами и меняют свой знак, оставляя значение у разницы тем же самым. Так что, можно связать второе решение квадратного уравнения с тройным углом.

Используя что
$m_1 = x_1 - d = -x_2\\ m_2 = x_2 - d = -x_1$

Получим
$\\d = x_1 + x_2 = 1 / 2$

И сразу получим остальные значения.

$\\x = (1 + \sqrt{5})/ 4 \;\;\;\;\;\;\;\;\;\; = \varPhi / 2 \;\;\;\;\;\;\;\;\;\;\;\; = \varphi / 2 + 1 / 2 \\y = \sqrt{(5 - \sqrt{5}) / 2} / 2 \;\;\; = \sqrt{3 - \varPhi} / 2 \;\;\;\; = \sqrt{2 - \varphi} / 2 \\m = (\sqrt{5} - 1)/ 4 \;\;\;\;\;\;\;\;\; = \varPhi / 2 - 1 / 2 \;\;\;\; = \varphi / 2 \;\;\;\;\;\;\;\;\;\; \\n = \sqrt{(5 + \sqrt{5}) / 2} / 2\;\;\; = \sqrt{2 + \varPhi} / 2 \;\;\;\; = \sqrt{3 + \varphi} / 2$

Число $\varphi$ это малый коэффициент золотого сечения.
Число $\varPhi$ это большой коэффициент золотого сечения.

Их основные свойства:
$\\\varphi ^ 2 = 1 - \varphi \\\varphi + 1 = \varPhi = 1 / \varphi \\1 + \varPhi = \varPhi ^ 2 \\\varphi + \varPhi = \sqrt{5} \\2\varphi + 1 = \sqrt{5} = 2\varPhi - 1$

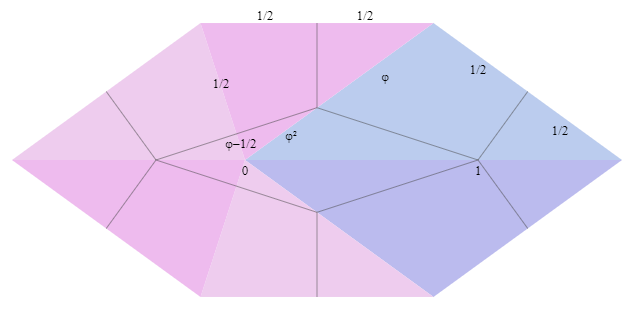
Координатная система в которой координаты целые числа, и при этом можно делать повороты на 36° определяется так:
$\{n_1,n_2,n_3,n_4\}=(n_1\cdot C_{xa}+n_2 \cdot C_{xb},n_3 \cdot C_{ya} + n_4 \cdot C_{yb})$

Используемые константы равны
$C_{xa} = 1 / 2 \\C_{xb} = \varphi / 2 \\C_{ya} = \sqrt{3 + \varphi} / 2 \\C_{yb} = \sqrt{2 - \varphi} / 2$

Это позволяет представить три базовых вектора $(1,0), (x,y), (m,n)$ как
$(2 \cdot C_{xa}\;\;\;\;\;\;,0\;\;\;) = \{2,0,0,0\}\\ (C_{xa}+C_{xb},C_{yb}) = \{1,1,0,1\}\\ (C_{xb}\;\;\;\;\;\;\;\;\;\;,C_{ya}) = \{0,1,1,0\}$

При комбинации единичных векторов групповая чётность координат сохраняется, и может быть только одного из следующих типов:
$\{0,0,0,0\},\{1,1,0,1\},\{0,1,1,0\},\{1,0,1,1\}$ .

То есть, на координаты накладываются ограничения
$x = k_1 + k_2\varphi \;\;\;\;\;\;\;\;\;\;\;\leftrightarrow y = k_3 K_3 + k_4 K_2 \\x = k_1 + k_2\varphi \pm \frac{1\pm\varphi}{2} \leftrightarrow y = k_3 K_3 + k_4 K_2 \pm \frac{K_2}{2} \\x = k_1 + k_2\varphi \pm \;\; \frac{\varphi}{2} \;\;\leftrightarrow y = k_3 K_3 + k_4 K_2 \pm \frac{K_3}{2} \\x = k_1 + k_2\varphi \pm \;\;\frac{1}{2} \;\;\leftrightarrow y = k_3 K_3 + k_4 K_2 \pm \frac{K_3 \pm K_2}{2}$

где $k$ — целые числа.
$\\K_3 = 2 C_{ya} = \sqrt{3 + \varphi} \\K_2 = 2 C_{yb} = \sqrt{2 - \varphi} \\K_3 K_2 = \sqrt{5} \\K_3 \varphi = K_2$

Преобразуя таблицу умножения

*	1	φ	K3	K2
1	1	φ	K3	K2
φ	φ	1-φ	K2	K3-K2
K3	K3	K2	3+φ	1+2φ
K2	K2	K3-K2	1+2φ	2-φ

можно получить целочисленную трёхмерную матрицу для умножения векторов.

Используя эту координатную систему мы позиционируем точки с идеальной точностью целых чисел.

Еще немного теории о связи чисел: степень числа фи и последовательность фибоначчи.

При всей схожести формул
$\varPhi^{n - 1} + \varPhi^{n} = \varPhi^{n + 1}$
$Ф_{n - 1} + Ф_{n} = Ф_{n + 1}$
они, конечно, различаются.

Функция $\varPhi^n$ это степенная функция, которая строго больше нуля. А в последовательности фибоначчи $Ф_n$ присутствует ноль, и из-за этого все предшествующие ему числа чередуют знак.

Для решения уравнения $f(x-1) + f(x) = f(x+1)$ подходит не только $f(x) = \varPhi^x$ , но и $f(x) = (-\varPhi)^{-x} = (-\varphi)^x$ . Причем, они подходят одновременно. $f(x) = k_1\varPhi^x+k_2(-\varphi)^{x}$ . Если $f(0) = 0$ и $f(-1)=f(1) = 1$ , то коэффициенты $k_1=\frac{1}{\sqrt5}, k_2=-\frac{1}{\sqrt5}$ .

Так что, существует формула, которая связывает последовательность фибоначчи и степенную функцию числа фи (формула бине):
$Ф_n = \frac{\varPhi^{n}}{\sqrt5} - \frac{\left(-\varphi\right)^{n}}{\sqrt5}$

Для чисел с положительными номерами значение задается преимущественно левым слагаемым, и правое выравнивает до целого числа. Для чисел с отрицательным номером основной вклад идёт от правого слагаемого.

Обратная формула, получения степени числа $\varPhi$ из последовательности фибоначчи:
$\varPhi ^ {n} = Ф_{n-1} + Ф_{n}\varPhi$

Для числа $\varphi$ , которое в высоких степенях приближается к нулю, используется различие знака чисел с отрицательными номерами и примерное равенство соотношения соседних чисел самому числу $\varphi$ .
$\varphi ^ {n} = Ф_{-n+1} + Ф_{-n}\varphi$

В системе целых координат это находит выражение в том, что базовые вектора с множителем
$\varphi^n$ выражаются в целых коэффициентах, взятых из последовательности фибоначчи:
$\varphi^n\;V_0 = \{2Ф_{-n+1},2Ф_{-n}\;\;,0\;\;\;\;\;\;\;\;,0\;\;\;\;\;\;\} \\\varphi^n\;V_1 = \{Ф_{-n+2}\;\;,Ф_{-n+1},Ф_{-n}\;\;\;,Ф_{-n-1}\} \\\varphi^n\;V_2 = \{Ф_{-n}\;\;\;\;\;,Ф_{-n-1},Ф_{-n+1},Ф_{-n}\;\;\;\}$
На такие вектора можно и делить.

Теперь можно попробовать составить треугольники.

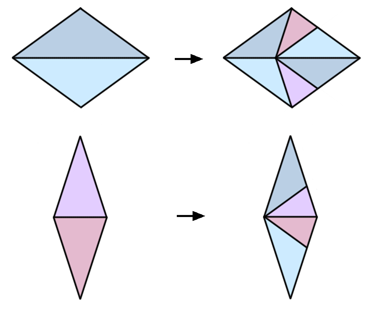
Треугольников в котором углы кратны 36° не так много, всего два. Сумма углов в треугольнике 180°, в долях сумма углов должна быть равна пяти. Как 5 поделить на три целых числа? Единица должна быть, потому что без нее даже минимум, три двойки — это уже перебор. Оставшиеся 4 доли можно поделить только как 1 + 3 и 2 + 2. Оба треугольника равнобедренные, имеют в себе пару одинаковых углов.

Обозначим треугольники как T1 и T2, в соответствии размера в долях того угла который повторяется.

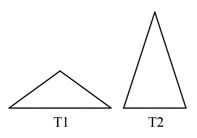
Теперь можно попробовать треугольники разбить.

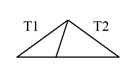
Треугольник T1 можно поделить на два треугольника: Т1 и Т2.

Треугольник T2 можно поделить на два треугольника: T1 и T2.

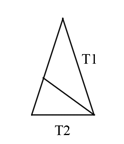
Треугольник T1 можно поделить еще и на три треугольника: T1, T2, T1. Причем, такого разбиения два: симметричное и антисимметричное.

Эти разбиения уменьшают боковые стороны треугольников на один и тот же коэффициент $\varphi$ .

Из таких треугольников можно построить мозаику пенроуза.

Для построения можно исходить из следующих правил:

1. Для каждого уровня разбиения все треугольники имеют одинаковую длину боковых сторон, а основанием соединены с таким же треугольником, который на более детальный уровень разбивается симметрично исходному. Именно из-за этого правила мозаику пенроуза можно представлять равносторонними ромбами.

2. Для разбиения треугольника T1 используется только несимметричный вариант.
Именно поэтому мозаику пенроуза можно представлять разбиением на дельтоиды:
У получившегося T1 обязательно есть парный треугольник, который образует с исходным уголок, «дротик» (dart). А у получившегося T2 парный треугольник вместе с соседним образуют выпуклый дельтоид «воздушный змей» (kite).

Хотя сами по себе могут быть получены делением ромба, дельтоиды в мозаике расположены так, что никогда не соединяются в ромб. У сложной формы дельтоидов есть преимущество: ромб при одной форме может иметь два возможных направления, а у дельтоидов оно задано явно.

Если у нас соединены треугольники Т1 и Т2, то дальнейшее построение имеет два варианта: либо они вместе образуют Т2 и значит на общем уровне он имеет свое отражение. Либо Т1 и Т2 составляют вместе часть разбиения Т1, и тогда продолжение выглядит менее симметрично.

Поэтому мозаику пенрозуа удобнее строить не достраиванием во вне, а делением внутрь.

Относительно деления треугольники различаются не только по форме, но и по направлению симметрии. «Правый» и «Левый» треугольники режутся противоположным образом. Поэтому надо сразу выяснить, какого типа треугольники получаются при самом делении.
Мы получим правила

$\\T_{1A} \rightarrow T_{1A}+T_{2A}+T_{1B} \\T_{1B} \rightarrow T_{1B}+T_{2B}+T_{1A} \\T_{2B} \rightarrow T_{1A}+T_{2B} \\T_{2A} \rightarrow T_{1B}+T_{2A}$

Получается, у ромбов четыре вида сторон: те которые при разбиении делятся — со сдвинутым местом разбиения вправо или влево, и те, которые не делятся, а образуют диагональ для Т1 — либо правого, либо левого. Зная какие стороны стыкуются можно раскрашивать плитки мозаики так, чтобы линии рисунка стыковались на границах, и тогда получаются симпатичные узоры.

У мозаики пенроуза несколько представлений, но как универсальный можно использовать вид из шести треугольников, четыре из которых повторяют показанное разбиение из треугольников, а два дополнительных, вида Т1, аналогичны по разбиению первому и второму, но отличаются тем, что на предыдущем уровне разбиения были частью Т1 точно такого же типа — левый из левого, правый из правого.

Такие треугольники можно объединять в различные виды мозаики: и в ромбы, и в дельтоиды, и в различающиеся стороной треугольники, и в фигуры HBS. А для представления Р1, для представления из прямых линий и для набора четырёхугольников нужно сопоставить двум базовым треугольникам линии разбиения.

Универсальный вид

Список представлений:

Из двух треугольников (четырёх видов) с одинаковыми боковыми сторонами
Из двух треугольников (четырёх видов) с различными боковыми сторонами
Из пары ромбов, представление Р3
Из ромба и уголка двух видов
Из пары дельтоидов, представление Р2: дротик/воздушный змей
Представление P1: четыре вида пятиугольников, звезда, лодочка
Представление «шестиугольник, лодка, звезда», HBS
Особое представление: просто пересекающиеся прямые линии
Семь четырёхугольников (Семь видов четырехугольников, количество форм только шесть)

Чтобы изобразить на компьютере мозаику достаточно в текстовом редакторе написать html-страничку с кодом на javascript и открыть эту страничку в браузере.

Весь текст странички без кода:

Получаем «контекст», объектный интерфейс для рисования на плоскости:

var canvas = document.getElementById("a");
var b = canvas.getContext("2d");

Программа будет рассчитывать фигуры, а потом их отрисовывать в зависимости от заданных настроек.

Функции для упрощения команд рисования:

// начать описание контура
function begin(){b.beginPath();}
// начать линию с точки
function from(p) {b.moveTo(s[8] + p[0], s[9] - p[1]);}
// привести линию к точке
function to(p){b.lineTo(s[8] + p[0], s[9] - p[1]);} 
// привести линию к начальной точке, не требуется если выполняется только заливка
function close(){b.closePath();}
// заливка
function fill(color){b.fillStyle = color; b.fill();}
// обводка контура линией
function line(){b.strokeStyle = "#444"; b.lineWidth = 0.5; b.stroke();}
function line_white(){b.strokeStyle = "#fff"; b.lineWidth = 1; b.stroke();}
function line_black(){b.strokeStyle = "#444"; b.lineWidth = 1.5; b.stroke();}

Мозаика будет состоять из фигур, они хранятся как массив данных: тип фигуры, от 0 до 5, координаты угла привязки, массив четырех целых чисел, и направление, 0 до 9. В функции отрисовки масштаб координат и размер шага рисования стороны фигуры задаются отдельно.

Прежде всего нужно задать используемые константы.

var s;
function prepare()
{
    var sqrt = Math.sqrt;
    var fi = (sqrt(5) - 1) / 2;
    var fb = (sqrt(5) + 1) / 2;
    var f3 = sqrt(3 + fi);
    var f2 = sqrt(2 - fi);
    //координаты базовых векторов для всех десяти направлений
    var vt = [[ 2, 0, 0, 0], [ 1, 1, 0, 1], [ 0, 1, 1, 0], [ 0,-1, 1, 0], [-1,-1, 0, 1],
              [-2, 0, 0, 0], [-1,-1, 0,-1], [ 0,-1,-1, 0], [ 0, 1,-1, 0], [ 1, 1, 0,-1]];
    // Константы множители координат
    var c = [1/2, fi/2, f3/2, f2/2]
    // Общий массив констант
    // нулевой элемент для контекста
    // седьмой для дополнительных данных рисования.
    // восьмой и девятый для указания центра рисования
    // десятый для размера шага.
    var s = [0, vt, c, fi, f3, f2, 0, 0, 0, 0];
    return s;
}

s = prepare();
s[0] = b; 
s[7] = 1;      // доля последнего уровня
s[8] = 500/2; // сдвих координаты x
s[9] = 320/2;  // сдвиг координаты y

Сначала зададим базовую фигуру из шести треугольников.

Код заполнения первого уровня

var f = []; // слои разбиения.
f[0] = [];
f[0].push([0,[ 0, 0, 0, 0],0]); 
f[0].push([1,[ 0, 0, 0, 0],0]);
f[0].push([2,[ 0, 0, 0, 0],3]);
f[0].push([3,[ 0, 0, 0, 0],3]);
f[0].push([2,[ 0, 0, 0, 0],7]);
f[0].push([3,[ 0, 0, 0, 0],7]);

Код расчета и отрисовки уровней


fi = s[3]; // берем из констант коэффициент
var levels = 3; // количество расчетных уровней
s[7] = 0.1 * 10; // степень проявления уровня
s[10] = 24 * 6 * fi * fi; // длина линии
//s[10] = 24 * 6 * fi
//s[10] = 24 * 6;

// для отображения полного поля нужно изменить размер шага, размер канвы, место центра и поменять местами p[0] и p[1] в функциях from() и to(). 
//s[10] = 24; 

mode = 12; // режим рисования

// разбиение
var n = 0, m;
for(; n < levels; n++) 
{   m = n + 1; 
    f[m] = []; 
    for(var k = 0; k < f[n].length; k++) 
        zd(f[n][k], s, f[m]);
}
// отображение
n = m - 1;
// предыдущий уровень
if(s[7] != 1) 
    for(var i = 0; i < f[n].length; i++) {paint(f[n][i], mode, 1);}
// последний уровень
for(var i = 0; i < f[m].length; i++) {paint(f[m][i], mode, 0);}
// Для 11 режима подчеркиваются линии
if(mode == 11) {d = 3; for(var i = 0; i < f[m-d].length; i++) {paint(f[m-d][i], mode, d);}}

Функция разбиения

function zd(a, s, f)
{
    var t = a[0]; // тип фигуры
    var vt = s[1]; // таблица векторов

    if (t > 3) t = t - 4; // типы фигур 4 и 5 обрабатываются как 0 и 1

    // направление первого шага в зависимости от типа фигуры, в виде смещения направления
    sht = [ 1,-1, 2,-2];
    var shift = sht[t];

         if(t == 0) {t1 = 0; t2 = 3; t3 = 5;} // типы получившихся фигур
    else if(t == 1) {t1 = 1; t2 = 2; t3 = 4;}
    else if(t == 2) {t1 = 4; t2 = 2;}
    else if(t == 3) {t1 = 5; t2 = 3;}

    if (t < 2)
    {
        pos = a[1];
        v1 = a[2]; // общее направление
        v2 = (v1 + shift + 10) % 10; // направление первого шага
        v3 = (v1 - shift + 10) % 10; // направление второго шага
        v4 = (v2 + 5) % 10; // обратное направление первому
        v5 = (v1 + 5) % 10; // обратное направление общему (не второму)
        
        p1 = add(pos, vt[v2]); // позиция после первого шага
        p2 = add(p1, vt[v3]);  // позиция после второго шага
        p3 = mul(p1,[2,2,0,0]); // масштабирование
        p4 = mul(p2,[2,2,0,0]); // масштабирование

        f.push([t1, p3, v4]);
        f.push([t2, p3, v3]);
        f.push([t3, p4, v5]);
    }
    else
    {
        pos = a[1];
        v1 = a[2];
        v2 = (v1 + shift + 10) % 10; // направление первого шага
        v3 = (v1 - shift + 10) % 10; // направление второго шага
        v4 = (v2 + 5) % 10; // обратное направление первому
        v5 = (v3 + 5) % 10; // обратное направление второму
        
        p1 = add(pos, vt[v2]); // позиция после первого шага
        p2 = add(p1, vt[v3]);  // позиция после второго шага
        p3 = mul(p1,[2,2,0,0]); // масштабирование
        p4 = mul(p2,[2,2,0,0]); // масштабирование

        f.push([t1, p3, v4]);
        f.push([t2, p4, v5]);
    }

    return f;
}

Используемые функции сложения и умножения векторов

function mul(v1, v2)
{
    mt = [[[1, 0, 0, 0],[0, 1, 0, 0],[ 0, 0, 1, 0],[ 0, 0, 0, 1]],
          [[0, 1, 0, 0],[1,-1, 0, 0],[ 0, 0, 0, 1],[ 0, 0, 1,-1]],
          [[0, 0, 1, 0],[0, 0, 0, 1],[-3, 1, 0, 0],[-1,-2, 0, 0]],
          [[0, 0, 0, 1],[0, 0, 1,-1],[-1,-2, 0, 0],[-2, 1, 0, 0]]]
    var v3 = [0, 0, 0, 0];
    for(var i = 0; i < 4; i++) 
        for(var j = 0; j < 4; j++) 
            for(var k = 0; k < 4; k++) 
                v3[k] = v3[k] + v1[i] * v2[j] * mt[i][j][k];

    for(var i = 0; i < 4; i++) v3[i] = v3[i] / 2;
        
    return v3;

}

function add(v1, v2)
{   // нельзя к первому к первому аргументу добавить второй и вернуть, 
    // потому что аргументы принимаются по ссылке и значит будут изменены.
    var v3 = [0, 0, 0, 0]; 
    for(var i = 0; i < 4; i++) v3[i] = v3[i] + v1[i];
    for(var i = 0; i < 4; i++) v3[i] = v3[i] + v2[i];
    return v3;
}

Функция нахождения точки между двумя, с заданным коэффициентом.

function mean(p1, p2, d)
{   var p3 = [(p2[0] - p1[0]) * d + p1[0],(p2[1] - p1[1]) * d + p1[1]];
    return p3;
}

Осталось задать режимы, как именно фигуры могут отображаться.

Функция отрисовки фигуры


function paint(a, mode, level = 0)
{
    vt = s[1];    // таблица векторов
    c  = s[2];    // массив координатных констант
    fi = s[3];    // константа фи
    pr = s[7];    // доля проявления уровня
    b  = s[0]; // контекст рисования
    
    var st = s[10];

    // шесть цветов на выбор
    colors = [["#BCE"],["#BBE"],["#ECE"],["#EBE"],["#CEF"],["#EEF"]];

    type = a[0]; // оригинальный тип фигуры
    tn = type;   // тип свернутый до 4
    if(tn > 3) tn = tn - 4;
    
    // цвет
    color = colors[type];

    // направление первого шага, в виде сдвига направления
    sht = [ 1,-1, 2,-2];
    var shift = sht[tn];

    p = a[1]; // точка привязки
    
    v0 = a[2]; // направление
    v0 = (10 + v0 % 10) % 10; // направление выравнено в пределы 0-10
    v1 = (10 + (v0 + shift) % 10) % 10; // направление первого шага
    v2 = (10 + (v0 - shift) % 10) % 10; // направление второго шага
    
    // коэффициенты масштабирования для позциции и для сторон.
    var kop = 0; 
    var koe = 0; 
    pr1 = 1 - pr; // доля предыдущего уровня.
    if(level == 0) {kop = st; koe = pr;}
    if(level == 1) {kop = st / fi; koe = pr1 / fi; } // проступание соседнего уровня
    
    if(level == 3) {kop = st / fi / fi / fi; koe = pr / fi / fi / fi; } // линии на три уровня меньше
        
    st = st * koe; // масштабирование фигур.

    // координаты начала линии
    p0 = [kop * (p[0] * c[0] + p[1] * c[1]), kop * (p[2] * c[2] + p[3] * c[3])]
    // координаты конца первой линии
    s1 = vt[v1]; p1 = [p0[0] + st * (s1[0] * c[0] + s1[1] * c[1]), p0[1] + st * (s1[2] * c[2] + s1[3] * c[3])];
    // координаты конца второй линии
    s2 = vt[v2]; p2 = [p1[0] + st * (s2[0] * c[0] + s2[1] * c[1]), p1[1] + st * (s2[2] * c[2] + s2[3] * c[3])];
    
    // таблица рисовать ли фон
    modes = [1, 1,1,1,1,1, 0,0,0,0,1, 1,1,1];
    y = modes[mode];

    // заливка, сразу можно грани рисовать
    if(level < 3) // если сдвинутый на три уровень, то фон не отрисовывается, только линии 11 режима.
    if(y || mode == 0)
    {   begin(); from(p0); to(p1); to(p2); close();
        if(y) {fill(color);}
        if(mode == 0) line();
        if(mode == 12) line_white();
    }
    
    // четырехугольники
    if(mode == 1) 
    {   p3 = mean(p0, p2, 0.5);
        begin(); from(p0); to(p2); from(p1); to(p3); line_black();
    }

    // дальняя сторона, фигуры HBS
    if(mode == 2) 
    {   begin(); from(p1); to(p2); line();
    }
    if(mode == 6) // ромбы
    {   begin(); 
        if(tn == 0 || tn == 2)
        {   color = colors[tn * 2];
            // четвертый угол ромба
            p3 = mean(p0, p2, 0.5);
            p4 = mean(p1, p3, 2);
            from(p0); to(p1); to(p2); to(p4); close(); fill(color);
        }
        line();
    }

    if(mode == 7) // дельтоиды
    {   if(type == 0)
        {   // расчет дополнительного угла уголка
            p3 = mean(p0, p1, 1 + fi);
            p4 = mean(p2, p3, 1 + fi);
            begin(); from(p0); to(p1); to(p4); to(p2); close(); fill(colors[0]); line();
        }
        if(type == 2)
        {   // расчет углов фигуры воздушный змей
            p3 = mean(p0, p2, 2 + fi)
            p4 = [p0[0] + (p2[0] - p1[0]), p0[1] + (p2[1] - p1[1])];
            begin(); from(p0); to(p1); to(p3); to(p4); close(); fill(colors[4]); line();
        }
    }

    if(mode == 8) // разные треугольники
    {   if(type < 2)
        {   begin(); from(p0); to(p1); to(p2); close(); fill(colors[0]); line();
        }
        if(type == 4 || type == 5)
        {   p3 = mean(p0, p1, 1 + fi);
            begin(); from(p0); to(p3); to(p2); close(); fill(colors[4]); line();
        }
    }

    if(mode == 9) // ромб и уголки
    {   if(type == 0)
        {   p3 = mean(p0, p1, 1 + fi);
            p4 = mean(p2, p3, 1 + fi);
            begin(); from(p0); to(p1); to(p4); to(p2); close(); fill(colors[0]); line();
        }
        if(type == 2)
        {   p3 = [p0[0] - p1[0] + p2[0], p0[1] - p1[1] + p2[1]];
            begin(); from(p0); to(p1); to(p2); to(p3); close(); fill(colors[4]); line();
        }

        if(type == 4)
        {   p3 = mean(p2, p1, 1 + fi);
            p4 = mean(p0, p3, 1 + fi);
            begin(); from(p0); to(p4); to(p1); to(p2); close(); fill(colors[0]); line();
        }
    }

    if(mode == 10)
    {
        p4 = mean(p1, p0, fi);
        p5 = mean(p0, p2, fi);
        p6 = mean(p2, p0, 1 / 2 + fi / 2);
        p7 = mean(p1, p2, 0.5);
        begin(); if(tn < 2) {from(p4); to(p5);} else {from(p6); to(p4);} to(p7); line();
    }

    if(mode == 11)
    {
        k1 = 1 / 2;  
        k2 = (fi + 1) / 2;
        k3 = (4 - fi) / 4;
        k4 = (fi + 1) / 4;
        k5 = (3 - 2 * fi) / 2;
        k6 = 1 / 4;
        if(tn < 2) 
        {
            p3 = mean(p0, p2, k4);
            p4 = mean(p0, p1, k2);
            p5 = mean(p1, p2, k1);
            p6 = mean(p0, p2, k5);
            p7 = mean(p1, p2, k3);
            begin(); from(p3); to(p4); to(p5); to(p6); to(p7);
        }
        else
        {   
            p3 = mean(p2, p1, k3);
            p4 = mean(p0, p1, k2);
            p5 = mean(p1, p2, k1);
            p6 = mean(p2, p0, k6);
            begin(); from(p3); to(p4); to(p5); to(p6);    
        }
        
        line();
    }        
}

Код можно скопировать со статьи в файл фрагмент за фрагментом и он заработает.

Так как каждый треугольник имеет парный треугольник (кроме тех, которые на границе), то для лучшей прорисовки можно добавить режим, в котором один из пары треугольников отображается ромбом, а второй не отображается. Так же можно сделать и с дельтоидами и с треугольником объединенным из двух.

Для разбиения P1 нужно задать по две линии на треугольник.

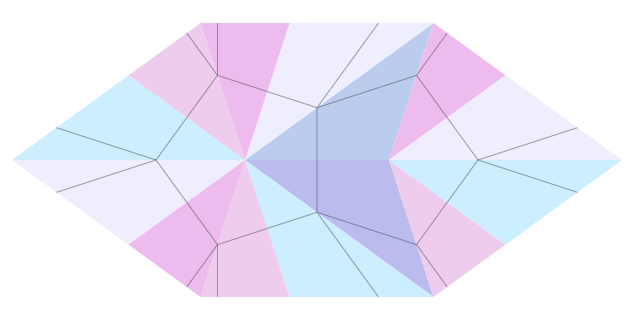
Для представления мозаики из линий нужно задать следующее разбиение:

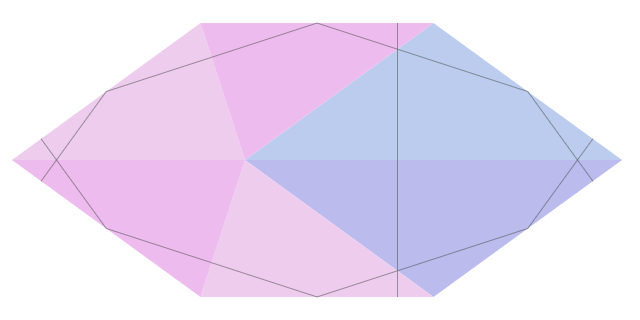
Через три уровня линии повторяются:

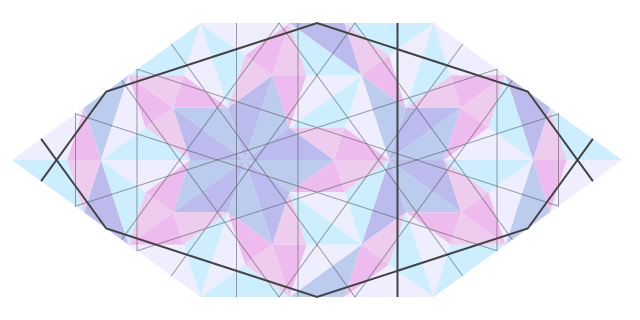
Из этого можно вывести коэффициенты пропорций деления линией сторон в месте пересечения. После смещения на три уровня сторона треугольника становится $\varphi^3 = 2\varphi - 1$ . Решая уравнение $k = 1 - k(2\varphi - 1)$ получим $k(1 + 2\varphi - 1) = 1$ , и коэффициент будет равен $k = \frac{1}{2\varphi} = \frac{\varPhi}{2}$ .
Получаются пропорции деления:
$K_1:\frac{1}{2} + \frac{1}{2} = 1$ — деление стороны посередине.
$K_2: \frac{\varPhi}{2} + \frac{1-\varphi}{2} = 1$ — деление единичной диагонали.
$K_3: \frac{5-\varPhi}{4} + \frac{\varphi}{4} = 1$ — проекция диагонали на сторону.
$K_4: \frac{\varPhi}{4} + \frac{3-\varphi}{4} = 1$ — первая проекция на диагональ широкого ромба.
$K_5: \frac{5 - 2\varPhi}{2} + \frac{2\varphi-1}{2} = 1$ — вторая проекция на диагональ широкого ромба.
$K_6: \frac{1}{4} +\frac{3}{4} = 1$ — проекция на диагональ узкого ромба

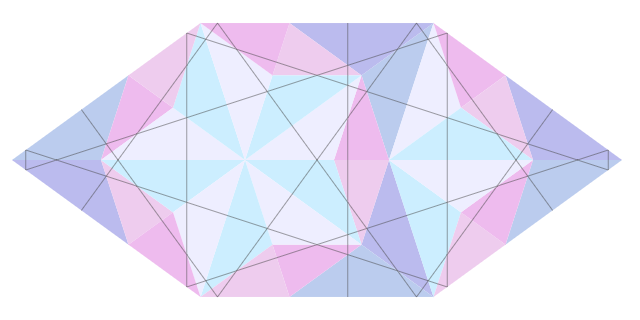
Оказывается, что треугольники, у которых совпадают углы привязки образуют фигуры HBS. И для отрисовки разбиения на HBS достаточно выводить дальнюю грань. Если треугольники масштабировать без изменения привязки, то вокруг фигур образуется пустое пространство. В этом пустом пространстве можно вывести фигуры предыдущего уровня, смасштабировав так, чтобы они касались фигур этого уровня. Именно так нарисовано первое изображение статьи.

Для вывода отображения из семи видов четырехугольников отрисовывается основание каждого треугольника и высота.

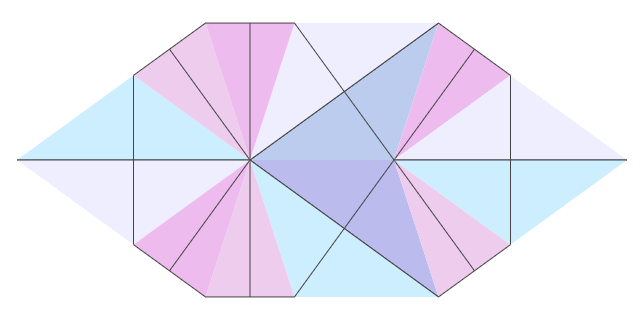
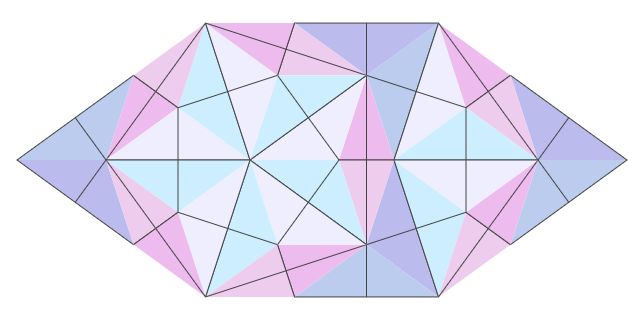
По-моему, очень красиво.