Тренировочный раунд RCC 2014 Warmup
 Очередной сезон крупнейшей российской олимпиады для программистов Russian Code Cup стартовал в субботу, 19 апреля 2014 года. Впереди новые интересные и нетривиальные задания, бескомпромиссная борьба и отличные призы.
Очередной сезон крупнейшей российской олимпиады для программистов Russian Code Cup стартовал в субботу, 19 апреля 2014 года. Впереди новые интересные и нетривиальные задания, бескомпромиссная борьба и отличные призы.
Жюри Russian Code Cup подготовило всем участникам один сюрприз: 17 апреля у каждого из них была возможность оценить свои силы. В 19:30 по московскому времени на площадке http://codeforces.ru состоялся тренировочный раунд олимпиады со свежей порцией задач от создателей RCC.
RCC 2014 Warmup — это тест, который дал возможность попробовать свои силы и понять, к чему готовиться в раундах чемпионата. А для «бывалых» участников он оказался идеальной возможностью потренироваться и разогреться перед первыми сражениями RCC 2014.
Причем если на Russian Code Cup задачи для участников предлагаются только на русском языке, то на Warmup Round задачи были как на русском, так и на английском языке, что существенно расширило географию проведения. Всего на раунд зарегистрировалось 3265 участников.
Условия задач были самыми разными: нужно было помочь с отбором участников на финал Russian Code Cup 2214 года, восстановить данные тестирующей системы после падения, провести футбольный турнир среди участников Russian Code Cup, помочь хитрому мальчику Гене получить футболку, решить интересное задание мальчика Миши во время путешествия на кораблике после финала Russian Code Cup, организовать финал Russian Code Cup 2214 года в большом числе гостиниц и добыть пароль для доступа к задачам во время их разработки (последнее так никому и не удалось).Итак, посмотрим, как можно было лучше всего подготовиться к участию в чемпионате.
Задача 1. Отбор
Разбор: Сначала нужно заметить, что если k больше либо равно, чем n•m, то ответ — 0. Нам осталось набрать n•m - k человек. Есть три способа их набрать:• Взять раунды только первого типа: 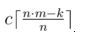 • Взять чуть раундов второго типа до числа, делящегося на n:
• Взять чуть раундов второго типа до числа, делящегося на n: 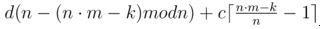 • Взять только раунды второго типа: d(n•m - k).Также в данной задаче можно было написать переборное решение — сколько мы берём раундов первого типа, и сколько раундов второго.
• Взять только раунды второго типа: d(n•m - k).Также в данной задаче можно было написать переборное решение — сколько мы берём раундов первого типа, и сколько раундов второго.
Задача 2. Сбой
Разбор: Заведём массив a на 105 элементов, изначально заполненный -1, и в ячейке с номером k будем хранить максимальный номер посылки k-го участника, который сейчас есть. Будем обрабатывать посылки последовательно. Пусть обрабатывается посылка xk. Если a[k] < x - 1, то очевидно, что ответ NO, иначе обновляем массив — a[k] = max(a[k], x).
Задача 3. Футбол
Разбор: Представим себе турнир как граф. Из каждой вершины ровно k выходящих рёбер. Тогда всего nk рёбер. В полном графе максимум 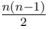 рёбер, поэтому если n < 2k + 1, тогда ответ -1. Иначе, соединим i-ую вершину с i + 1, ..., i + k, и зациклим, если нужно.
рёбер, поэтому если n < 2k + 1, тогда ответ -1. Иначе, соединим i-ую вершину с i + 1, ..., i + k, и зациклим, если нужно.
Задача 4. Хитрый Гена
Разбор: Давайте отсортируем друзей по возрастанию требуемого количества мониторов. Будем считать динамику на масках — какое минимальное число денег нужно заплатить, чтобы решить такие-то задачи, если мы взяли первых i друзей. Тогда ответ надо сравнить с ответом для i первых друзей плюс количество мониторов, которое требует i-ый друг. Не трудно заметить, что если брать друзей последовательно, то пересчитывать динамику можно как рюкзак. Время работы данного алгоритма O(nlog(n) + n2m).
Задача 5. Квадратная таблица
Разбор: Давайте для любого n построим массив длины n, что сумма квадратов чисел на нём является квадратом:• Если n = 1, то берём [1].• Если n = 2, то берём [3, 4].• Если n чётно, то берём 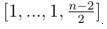 .• Если n нечётно, то берём
.• Если n нечётно, то берём 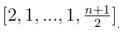 .Нам дано 2 числа n и m. Пусть массив a соответствует числу n, а b соответствует числу m.Тогда итоговый массив c построим следующим способом — cij = ai•bj.
.Нам дано 2 числа n и m. Пусть массив a соответствует числу n, а b соответствует числу m.Тогда итоговый массив c построим следующим способом — cij = ai•bj.
Задача: 6. Большие проблемы организаторов
Разбор: В данной задаче есть два решения.Первое. Подвесим за какую-нибудь вершину. Предподсчитаем для каждой 3 самые удалённые вершины в её поддереве, а также глубину для каждой вершины. Также предподсчитаем массивы для двоичного подъёма. Для каждой вершины i и степени двойки 2j предподсчитаем следующие массивы — p[i][j], up[i][j] и down[i][j]. p[i][j] — это предок вершины i на расстоянии 2j. В up[i][j] будет храниться наидлиннейший путь из i, до вершин, которые находятся в поддереве вершин, которые находятся на пути между i и p[i][j]. down[i][j] отличается от up[i][j], что хранит путь из вершины p[i][j].Теперь осталось дело за малым. Нам приходит запрос u v, мы ищем его наименьшего общего предка — w. Осталось найти вершину hu, которая будет находиться на середине это пути. Обрезать дерево по этой вершине, и посчитать длиннейшее расстояние от вершины u в её дереве и длиннейшее расстояние от вершины v в её дереве. Представляя на дереве это, если мы не будем удалять, то можно воспользовавшись нашими предподсчитанными массивами аккуратно пересчитать значение длиннейшего пути.Решение за O(nlog(n)).Второе. Вкратце. Найдём диаметр этого дерева. Предподсчитаем там ответ на префиксе для каждой вершины. Тогда при ответе на запрос мы находим, когда путь выливается в диаметр. На этом отрезке находим среднюю вершину, а далее отвечаем на запрос на префиксе или суффиксе.
Задача: 7. Хитрый парольРазбор: Ключевая теоретическая идея данной задачи заключается в том, что 2 строка совпадает с 4, 3 с 5 и т. д. Поэтому нам нужно уметь менять что-то только на первых трёх строках.Теперь дело остаётся за практической частью. В первую очередь сожмём все значения, чтобы они не превосходили 105. Разобьём массив на отрезки длиной LEN. На каждом отрезке будем считать следующее — для каждого значения будем хранить сколько раз он встречался на префиксе cnt, а так же дерево Фенвика, в котором в ячейке f[k] будет храниться количество чисел на данном префиксе, встречающихся ровно k раз. Несложно заметить, что в первом массиве хранится ответ на запросы ко второй строке, а чтобы получить ответ для третьей строки, нужно посчитать f[cnt[k]… 105]. Понятно так же, как делать пересчёт данной динамики.Итого, получаем время на запрос за 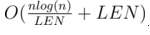 . Если мы возьмём
. Если мы возьмём 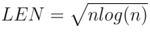 , то время ответа на запрос составит
, то время ответа на запрос составит 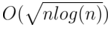 .
.
