Трехмерные фигуры Сома как идея для детского конструктора
В прошлой публикации мы рассмотрели новый замок для кубиков из нашего конструктора. Очередное применение кубикам правильной формы мы нашли для построения фигур Сома. Все было как всегда: кто-то сказал, что это было идеально, а мы полезли в интернет и поняли, что это не просто идеально, а, практически, единственное правильное решение использовать для этого конструктор открытого проекта Куботроник. Более того, покупные решения обходятся не дешевле. Но обо всем по порядку.Идеально, т.к. после соединения кубиков для получения нужных блоков НИЧЕГО не выступает.

После беглого ознакомления с источниками в интернете мы попали на официальную страницу кубиков Сома, по версии Википедии. В других источниках, в том числе, в книге Гарднер Мартин «МАТЕМАТИЧЕСКИЕ ГОЛОВОЛОМКИ И РАЗВЛЕЧЕНИЯ» 1971 года, были даны подробное обоснование уникальности предложенной концепции и примеры решений.Вот цитата из книги: «Китайская головоломка танграм, известная вот уже несколько тысячелетий, представляет собой квадрат из какого-нибудь материала, определенным образом разрезанный на семь частей. Игра заключается в том, что из семи элементов складывают различные фигурки. Время от времени предпринимались попытки создать трехмерные аналоги танграма, но ни одна из них не может сравниться с кубиками Сома, изобретенными датчанином Питом Хейном, о чьих математических играх гексе и так-тиксе мы уже рассказывали.
Кубики Сома Пит Хейн придумал во время лекции Вернера Гейзенберга по квантовой механике. Пока знаменитый физик говорил о пространстве, разрезанном на кубики, живое воображение Пита Хейна подсказало ему формулировку любопытной геометрической теоремы: если взять все неправильные фигуры, которые составлены из трех или четырех кубиков, склеенных между собой гранями, то из них можно составить один кубик большего размера.»

Событие это произошло в 1933 году, и с тех пор кубики активно продвигаются в массы, в том числе детские. В России эти кубики известны как «Кубики Никитина», которые он описал в своих книгах по развивающим занятиям с детьми.

В общем, задача стоит так: либо сложить что-то симметричное, либо по образцу, либо из ограниченного количества деталей, ну, или совсем что-то, на что-то не похожее и оригинальное:)
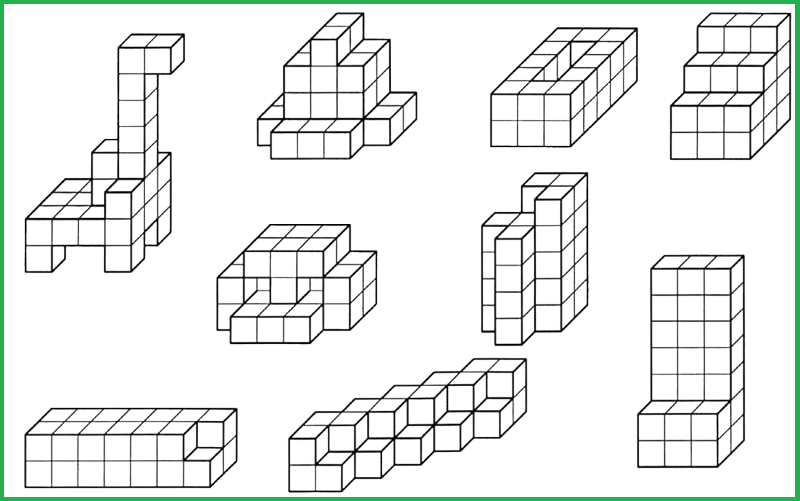
Покупные кубики, как правило, деревянные или пластмассовые и уже склеены нужным образом. Цена по данным Яндекс.Маркета начинается от 350р и до 800р, т.е. КУБОТРОНИК, изготовленный самостоятельно, тут тоже активно может конкурировать по стоимости.
Кроме того, у решения из Куботроника есть преимущество, что, во-первых, напечатав разными цветами кубики для каждой фигуры, их впоследствии можно перемешать и тем самым усложнить задачу для ребенка.

Более того, если отдельно добавить еще элементов или пересобрать имеющиеся 27 кубиков, то можно решать разные задачи, на примерах объясняющие детям основы геометрии простейших фигур и знакомить с понятиями грань, ребро, площадь, объем. Причем кубик Куботроника приобретает функцию единицы объема.

А вот ниже пример трансформации КУБА 2×2х2 в ПАРАЛЛЕЛЕПИПЕД 2×2х3.

Скачать STL файлы для изготовления кубиков вы можете на нашем сайте.
Источники: ВикиОф.страница с примерамиКнига Гарднер Мартин «МАТЕМАТИЧЕСКИЕ ГОЛОВОЛОМКИ И РАЗВЛЕЧЕНИЯ» 1971 г. Сайт Никитина Б.П.
