Талант против удачи: роль случайности в успехе и провале

Недавно я натолкнулся на интересную работу итальянских учёных о сильно недооценённой роли удачи и случайности в нашей жизни. К сожалению, не нашёл полной версии на русском языке (может, плохо искал?), но очень уж хотелось поделиться прочитанным со своими не владеющими английским товарищами. Поэтому, засучив рукава, принялся за свой кустарный перевод. Авторы, Аллесандро, Алессио и Андреа, любезно разрешили опубликовать его в общем доступе, поэтому, если заинтересовались, добро пожаловать под кат.
Авторы
- А. Плучино — кафедра физики и астрономии, Катанийский университет и Катанийский филиал Национального института ядерной физики, Италия; alessandro.pluchino@ct.infn.it
- А.Е. Биондо — кафедра экономики и бизнеса, Катанийский университет, Италия; ae.biondo@unict.it
- А. Раписарда — кафедра физики и астрономии, Катанийский университет и Катанийский филиал Национального института ядерной физики, Италия; Центр изучения сложных систем, Вена; andrea.rapisarda@ct.infn.it
Аннотация
В значительной степени доминирующая меритократическая (меритократия — принцип управления, согласно которому руководящие посты должны занимать наиболее способные люди, независимо от их социального происхождения и финансового достатка) модель высококонкурентных Западных культур берет начало из веры в то, что успех в основном, если не полностью, зависит от личных качеств, таких как талант, интеллект, навыки, находчивость, трудолюбие, упорство, тяжёлый труд или принятие рисков. Порой мы готовы признать, что определенная доля удачи тоже может играть роль в достижении значительного материального успеха. Но, по правде говоря, довольно часто недооценивается важность внешних сил в отдельных историях успеха. Хорошо известно, что интеллект (или, в общем, талант и личные качества) в популяции имеет гауссово распределение, в то время как распространение ценностей — часто рассматриваемое в качестве мерила успешности — обычно следует степенной зависимости (закону Парето), когда большинство являются бедняками и есть ничтожно малое количество миллиардеров. Такое расхождение между нормально распределенными входными данными, имеющими обычный уровень (усредненные талант или интеллект) и неизменным распределением на выходе, наводит на мысли, что где-то за кулисами имеется невидимый компонент. В данной работе, на основе крайне простого и игрушечного агентного моделирования, мы делаем предположение, что таким компонентом является обычная случайность. В частности, мы показываем, что, хотя для жизненного успеха действительно и правда требуется некоторая доля таланта, но самые одарённые люди практически никогда не достигают высочайших вершин благосостояния, будучи обогнанными посредственными, но намного более удачливыми личностями. Насколько нам известно, этому противоречащему здравому смыслу результату — хотя и неявно предполагаемому между строк много в какой литературе — именно тут впервые дана количественная оценка. Это позволяет по-новому взглянуть на эффективность оценки достоинств на основе уже достигнутого уровня успеха и подчеркивает риски распространения чрезмерных почести или ресурсов людям, которые, в конечном счёте, могли оказаться просто удачливей остальных. При помощи данной модели также рассматриваем и сравниваем несколько поведенческих гипотез, чтобы показать наиболее эффективные стратегии государственного финансирования исследований, с целью для улучшения меритократии, разнообразия и инновационности.
1. Введение
Повсеместность степенной зависимости во многих физических, биологических или социо-экономических сложных системах можно рассматривать как нечто вроде отличительного математического признака тесной взаимосвязи их динамичной характеристики с масштабно-неизменяемой топологической структурой [1, 2, 3, 4]. В социо-экономическом контексте, по работе Парето [5, 6, 7, 8, 9], хорошо известно, что распределение богатств имеет характер степенной зависимости, чья характерная сильно вытянутая форма отражает глубину существующей пропасти между богачами и бедняками нашего общества.
Недавний отчет [10] показывает, что на сегодня данный разрыв намного больше, чем мы опасались: восемь людей владеют теми же богатствами, что и 3,6 миллиарда человек, составляющих беднейшую часть человечества. За последние 20 лет было выработано несколько теоретических моделей, вычисляющих распределение ценностей в контексте теории вероятностей и физической статистики, часто принимающих вид мультиагентного моделирования с простыми внутренними динамиками [11, 12, 13, 14, 15, 16, 17].
Двигаясь дальше в этом направлении, если рассматривать личное богатство как мерило успеха, то можно утверждать, что глубоко ассиметричное и неравное его распределение среди людей является следствием их естественных различий в таланте, навыках, компетенции, интеллекте, способностях или мере их упорства, трудолюбия, либо целеустремлённости. Такое предположение, в неявной форме, является основой так называемой меритократичной парадигмы: оно влияет не только на то, каким образом наше общество предоставляет возможности трудоустройства, чествование и славу, но также на стратегии, принятые правительствами для распределения ресурсов и финансирования тем, кто считаются наиболее заслуженными личностями.
Однако, предыдущий вывод, похоже, сильно расходится с подтверждёнными данными, что упомянутые выше свойства и качества людей нормально распределены по всей популяции, т.е., соответствуют симметричному Гауссовому распределению относительно данного среднего. Например, интеллект, каким он измеряется посредством тестов на IQ, соответствует следующему шаблону: средний IQ равен 100, но ни у кого нет IQ 1000 или 10000. То же относится к труду, считаемому в рабочих часах: кто-то работает больше среднего, другой меньше, но не существует того, кто трудится в миллиард раз больше часов по сравнению с остальными.
Зато в наше время появляется все больше доказательств касательно основополагающей роли шанса, удачи или, обобщая, случайных факторов, в определении успехов или провалов в наших личных и профессиональных делах. В частности, было показано, что все ученые имеют одинаковый шанс опубликовать в течение карьеры прорывную работу [18]; что те, у кого первая буква фамилии находится ближе к началу алфавита, намного вероятней получат должность начальника отдела [19]; что распределения библиометрических показателей, собранные учеными, могут оказаться случайными и бессмысленными из-за растущего явления, связанного с инфляционным механизмом «публикуйся или погибай» [20]; что позиция кого-либо в отсортированном по алфавиту списке может оказаться важной при определении доступа к ограниченным по количеству мест публичным сервисам [21]; что начальная буква отчества поднимает оценку интеллектуальных способностей [22]; что людей с легко произносимыми именами оценивают более положительно, чем тех, чьи имена сложные [23]; что те, чьи имена звучат более аристократично, чаще остальных работают в качестве руководителей, а не подчинённых [24]; что женщины с мужскими прозвищами более успешны в юридической профессии [25]; что примерно половина различий в доходах среди людей всего мира объясняется исключительно их страной проживания и распределением зарплат внутри соответствующей страны [26]; что на вероятность стать директором сильно влияют ваши имя и месяц рождения [27, 28, 29]; что инновационные идеи являются результатом случайных реакций в клетках нашего мозга [30]; и что даже вероятность развития рака, вполне возможно, разрушающего великолепную карьеру, по большей части зависит от неудачливости [31, 32]. Последние работы на тему репродуктивного успеха в течение жизни способствуют подтверждению таких высказываний, показывая, что, если отклонения признаков могут влиять на судьбу популяции в целом, то жизнь конкретных особей зачастую определяет удача.
В последние годы многие авторы, среди которых есть статистик и аналитик рисков Нассим Талеб [35, 36], инвестиционный стратег Майкл Мобуссин [37] и экономист Роберт Франк [38], исследовали в ряде популярных книг связь между удачей и мастерством в финансовых операциях, бизнесе, спорте, искусстве, музыке, литературе, науке и многих других областях. Они пришли к заключению, что случайные события играют гораздо большую роль в жизни, чем многие могли бы себе вообразить. На самом деле, они не предполагают, что успех не зависит от таланта и приложенных усилий, так как в крайне конкурентных областях или рынках типа «победитель забирает все», где мы живем и работаем в данное время, наиболее результативные люди практически всегда при этом необычайно талантливы и трудолюбивы. Они лишь заключили, что таланта и усилий недостаточно: вам также необходимо оказаться в нужном месте в нужное время. Короче говоря, удача также влияет, хотя её роль практически всегда недооценивается успешными людьми. Такое происходит из-за того, что случайность часто срабатывает неочевидным образом, поэтому легко сопоставить события, которые покажут успех как нечто, являвшееся неизбежным. Талеб называет такую наклонность «сказательным заблуждением» [36], а социолог Пол Лазарсфельд предложил термин «предвзятая ретроспектива». В своей последней книге, «Все очевидно: когда вы знаете ответ» [39], социолог и пионер науки о сетях Дункан Ваттс предполагает, что и сказательное заблуждение, и предвзятая ретроспектива апеллируют к особому явлению, при котором люди, видящие необыкновенно успешные результаты, считают их за несомненный продукт упорной работы и таланта. Однако успех, в основном, возникает путём сложных и переплетённых шагов, каждый из которых зависит от предыдущих: если бы какой-то из них отличался, вся карьера или жизненный путь практически наверняка также оказались бы другими. Данный аргумент также основывается на результатах новаторского экспериментального исследования, проведённого несколькими годами ранее самим Ваттсом совместно с другими авторами [40], в котором успех ранее неизвестных песен на искусственном музыкальном рынке, как было показано, не коррелировал с качеством самого произведения. А это, несомненно, сильно затрудняет любые предсказания, что показано в другом, более свежем исследовании [41].
В данной работе, при помощи агентного статистического подхода, мы попробуем практически количественно определить роль удачи и таланта в успешных карьерах. В разделе 2, на основе минимального количества допущений, а именно Гауссова характера распределения таланта [42] и мультипликативных динамиках как успехов, так и неудач [43], мы представим простую модель, которую назвали моделью «Талант против Удачи» (ТпУ), в которой имитируется развитие профессиональных карьер группы людей на протяжении 40-летнего периода их работы. Модель показывает, что в реальности, случайность играет фундаментальную роль при определении наиболее успешных личностей. Истинным является то, что, как и можно было ожидать, талантливые люди вероятней станут богатыми, известными или значимыми в течение собственной жизни, по отношению с менее подготовленными. Но, и это менее интуитивное объяснение, обычным людям с заурядным уровнем таланта статистически предначертано становиться успешными (т.е. располагаться на конце какого-нибудь степенного распределения успешности) гораздо чаще, нежели самым талантливым, при условии, что они становились любимчиками фортуны на протяжении своей жизни. Этот факт встречается часто, как указано в ссылках [35, 36, 38], но, насколько нам известно, впервые смоделирован и измерен именно в данной работе.
Успешность людей с заурядным талантом ставит под вопрос «меритократическую» парадигму и все те стратегии и механизмы, которые давали больше вознаграждений, возможностей, чествования, славы и ресурсов людям, считающимся лучшими в их области [44, 45]. Дело в том, что, в подавляющем большинстве случаев, все оценки чьего-либо таланта давались постфактум, исключительно по взгляду на его / её деятельность, или достигнутые результаты, в какой-то конкретной области нашего общества, вроде спорта, бизнеса, финансов, искусства, науки и т.д. Такой вид вводящей в заблуждение оценки приводит к подмене причины и следствия, оценивая в качестве самых талантливых людей тех, кто, попросту, наиболее удачливы [46, 47]. В соответствии с этим взглядом, в предыдущих работах предупреждалось о подобных видах «недалёкой меритократии» и показалась эффективность иных стратегий, основанных на случайных выборках во множестве различных сред, таких как менеджмент, политика и финансы [48, 49, 50, 51, 52, 53, 54, 55]. В разделе 3 мы применяем наш подход и делаем наброски по сравнению возможных схем распределения общественных средств в контексте научного исследования. Мы изучаем последствия различных стратегий распределения, среди которых есть и «недалёко» меритократичная, с целью исследования новых способов повышения, одновременно, минимального уровня успешности наиболее талантливых людей общества и итоговой эффективности государственных расходов. Мы также исследуем, в общем, как предлагаемые средой возможности, представленные в виде уровней образования и дохода (т.е., внешних факторов, зависящих от страны и социального слоя, из которого происходят люди), имеют значение в повышении вероятности успеха. Завершают работу финальные замечания.
2. Модель
Далее мы предлагаем агентную модель, названую «Талант против Удачи» (ТпУ), основывающуюся на небольшом количестве допущений, и преследующую цель описать эволюцию карьер группы людей под влиянием случайно происходящих удачных и неудачных событий.

Рисунок 1: Пример исходных параметров для нашей симуляции. Все симуляции, представленные в данной работе, были проведены в агентной среде моделирования NetLogo [56]. N = 1000 людей (агентов), с различной степенью таланта (интеллект, навыки и т.д.), случайным образом распределённых по фиксированным позициям внутри квадратного мира из 201×201 участков с условиями цикличных границ. Во время каждой симуляции, которая охватывает несколько десятков лет, они подвергаются воздействию определённого количества NE удачных (зелёные кружки) и неудачных (красные кружки) событий, перемещающихся по всему миру по случайным траекториям (случайное блуждание). В данном примере NE = 500.
Мы рассматриваем N индивидов, с талантом Ti (интеллект, навыки, способности и т.д.), имеющим нормальное распределение в интервале [0; 1] вокруг данного среднего mT со стандартным отклонением σT, случайным образом расставленных по фиксированным позициям внутри квадратного мира (см. рисунок 1) с условиями цикличности границ (т.е. с тороидальной топологией) и окруженных определённым количеством NE «передвигающихся» событий (отмеченных точками), какие-то из которых удачные, другое нет (нейтральные события в данной модели не учтены, так как они не имеют никаких существенных последствий на жизнь индивидуума). На рисунке 1 мы показали данные события в виде цветных точек: удачные зеленым и с относительным процентом pL, а неудачные красным и с процентом (100 − pL). Общее количество событийных точек NE распределено равномерно, но, разумеется, подобное распределение будет идеально однородным только для NE → ∞. В наших симуляциях обычно будет NE ≈ N/2, поэтому в начале каждой симуляции имеет место случайная значительная концентрация удачных или неудачных событийных точек в различных областях мира, в то время как другие области окажутся более нейтральными. Последующее случайное перемещение точек внутри квадратной матрицы, т.е., мира, не меняют данной фундаментальной особенности модели, что показывает на различное количество событий удачи или неудачи для разных людей на протяжении их жизни, не зависящее от их личного таланта.

Рисунок 2: нормальное распределение таланта среди популяции (с медианой mT = 0,6, показанной прерывистой вертикальной линией, и стандартным отклонением σT = 0,1 — значения mT ± σT отображены в виде двух точечных вертикальных линий). Данное распределение выделено в интервале [0; 1] и не меняется на протяжении симуляции.
В одной прогонке симуляции рассматривается период трудовой жизни P, равный 40 годам (в возрасте от двадцати до шестидесяти лет), с временным шагом δt, равным шести месяцам. В начале симуляции всем агентам выдан одинаковый капитал Ci = C (0) Ɐi = 1, …, N, представляющий их стартовый уровень успешности / благосостояния. Данный выбор преследует очевидную цель не дать никому первоначального преимущества. В то время как таланты агентов не зависят от времени, их капитал меняется. Во время развития данной модели, т.е., в течение предполагаемого периода жизни агентов, все событийные точки случайным образом передвигаются по миру и, при этом, возможно, пересекаются с местоположением каких-то агентов. Если вдаваться в подробности, то всякий раз каждая событийная точка покрывает, в случайном направлении, расстояние из 2 участков. Мы считаем, что происходит пересечение с индивидом, если событийная точка, представленная внутри круга с радиусом в один участок, центром находится на агенте (событийные точки после пересечения не исчезают). В зависимости от такого происшествия, в данном временном шаге t (т.е., каждые шесть месяцев), с определённым агентом Ak возможны три следующих варианта действий:
- Никакая событийная точка не пересекает позицию агента Ak — это означает, что в течение последних шести месяцев не происходило подобных событий, агент Ak не выполняет никакого действия.
- Позицию агента Ak пересекает удачное событие — это значит, что за последние шесть месяцев случилось удачное событие (обратите внимание, в соответствии со ссылкой [30], генерация инновационной идей здесь также считается удачным событием, случившимся в мозгу агента); как следствие, агент Ak удваивает свои капитал / успешность с вероятностью, пропорциональной его таланту Tk. Увеличение будет Ck (t) = 2Ck (t − 1), но только если rand[0; 1] < Tk, т.е., если агент достаточно умен, чтобы получить выгоду от подвернувшейся удачи.
- Неудачное событие пересекает позицию агента Ak — это означает, что в течение последних шести месяцев произошло неудачное событие; как следствие, агент Ak теряет половину своих капитала / успешности, т.е. Ck (t) = Ck (t − 1) / 2.
Приведённые выше правила для агентов (включая выбор деления изначального капитала пополам в случае неудачных событий и удвоения при удачных, пропорционально таланту агента), намеренно просты и могут считаться широко распространёнными, так как как они основаны на очевидном факте, что успех в повседневной жизни имеет свойство как расти, так и снижаться в стремительном темпе. Более того, данные правила дают значительное преимущество высокоталантливым людям, так как те могут извлечь больше выгоды из возможностей, представляемых удачей (включая способность использовать хорошую идею, зародившуюся в их мозгах). С другой стороны, к примеру, автомобильная катастрофа или внезапная болезнь, всегда являются неудачными событиями, в которых талант не имеет значения. В этой связи, мы можем вывести более точное определение «таланта», определив его как «любое личное качество, которое повышает шанс ухватиться за возможность». Иными словами, под термином «талант» мы, в широком смысле, подразумеваем интеллект, навыки, находчивость, упорство, решимость, трудолюбие, принятие рисков и так далее. Далее мы увидим, что преимущество наличия великого таланта является обязательным, но недостаточным условием достижения очень высоких вершин успеха.
2.1. Результаты одной прогонки
В данном подразделе мы привели результаты прогонки одной типичной симуляции. Вообще говоря, эти результаты довольно устойчивы, поэтому, как мы покажем далее, их можно считать в значительной степени репрезентативными для общих рамок, выходящих из нашей модели.
Давайте представим N = 1000 агентов с равным количеством начального капитала C(0) = 10 (в абстрактных единицах) и с фиксированным талантом Ti ϵ [0; 1], следующим нормальному распределению со медианой mT = 0,6 и стандартным отклонением σT = 0,1 (см. рисунок 2). Как было сказано ранее, симуляция охватывает реалистичный отрезок времени P = 40 лет, развиваясь равными шагами, по шесть месяцев каждый, всего из I = 80 итераций. В данной симуляции мы взяли NE = 500 событийных точек, с вероятностью наступления удачных событий pL = 50%.
По окончании симуляции, как видно из схемы (а) рисунка 3, мы выяснили, что простые динамические правила модели способны произвести неравноценное распределение капитала / успешности, с большим количеством бедных (неудачливых) агентов и малым числом крайне богатых (успешных). Построив то же распределение в билогарифмическом масштабе, на схеме (b) этого же рисунка видим распределение по степенной функции в духе Парето, наклон которой соответствует функции y© ≈ C−1,27.
Таким образом, несмотря на нормальное распределение таланта, модель ТпУ, похоже, смогла ухватить первую важную особенность, наблюдаемую при сравнении с реальными данными: имеющийся глубочайший разрыв между богатыми и бедными и неизменную природу его масштаба. В частности, в нашей симуляции только 4 индивида получили более 500 единиц капитала, а 20 самых успешных людей владеют 44% всех ценностей, в то время как почти у половины популяции осталось менее 10 единиц. В целом, соблюдается правило Парето »80/20», так как у 80% популяции во владении находится лишь 20% всего капитала, в то время как оставшимся 20% индивидов досталось 80% богатств. Хотя данное неравенство, несомненно, выглядит несправедливым, было бы в некоторой степени приемлемым, если большинство преуспевших людей оказались из числа самых талантливых, таким образом заслужив накопления большего капитала / успешности, по сравнению с остальными. Но так ли происходит на самом деле?
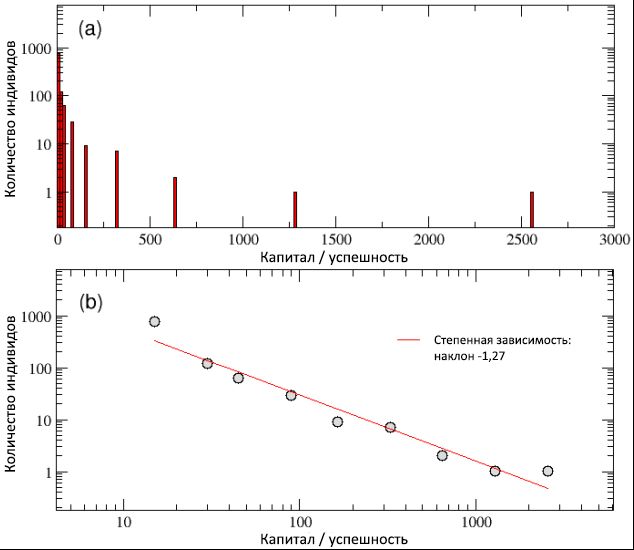
Рисунок 3: итоговое распределение богатств / успешности среди популяции, в логарифмически линейном (a) и билогарифмическом (b) масштабах. Несмотря на нормальное распределение таланта, хвост распределения успешности — как видно из схемы (b) — может быть описан в виде кривой степенной зависимости с наклоном −1,27. Мы также подтвердили, что распределение капитала / успешности следует закону Парето »80/20», так как 20% популяции владеет 80% ценностей и наоборот.
На рисунке 4, схемах (a) и (b), соответственно, отображены талант в виде функции от итоговых капитала / успешности, и наоборот (обратите внимание, что на схеме (a) капитал / успешность имеет только дискретные значения — это связано с решением использовать одинаковый для всех агентов начальный капитал). При взгляде на обе схемы видно, что, с одной стороны, наиболее успешные индивиды не являются самыми талантливыми и, наоборот, наиболее одаренные личности не являются самыми преуспевающими. В частности, наиболее успешный индивид, с Cmax = 2560, обладает талантом T* = 0,61, что лишь немногим выше медианного значения mT = 0,6, в то время как самый одарённый (Tmax = 0,89) имеет капитал / успешность меньше, чем 1 единицу (C = 0,625).
Как мы подробней узнаем из следующего подраздела, такой результат является не частным случаем, а, скорее, правилом для систем подобного типа: максимальный успех никогда не сходится с максимальным талантом, и наоборот. Более того, такое расхождение между успехом и талантом является непропорциональным и в высокой степени нелинейным. Фактически, средний капитал всех людей с талантом T > T* имеет значение C ≈ 20; другими словами, капитал / успешность наиболее преуспевающих людей с умеренными талантами в 128 раз выше, чем средние капитал / успешность людей, являющихся гораздо более одарёнными, чем первые. Мы можем заключить, что если за причиной огромного успеха некоторых людей не скрыт исключительный талант, то, возможно, имеет место другой фактор. Наша симуляция ясно показывает, что таким фактором является чистое везение.
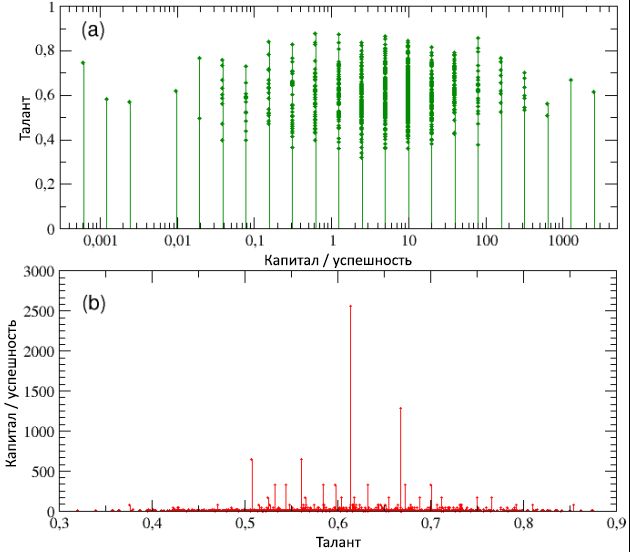
Рисунок 4: на схеме (а) талант отображён как функция капитала / успешности (в логарифмическом масштабе, для лучшей наглядности) — она свидетельствует, что самые успешные личности не являются, одновременно, и наиболее талантливыми. На схеме (b), наоборот, капитал / успешность показаны в виде функции от таланта — тут можно лучше оценить факт, что самый успешный агент, с Cmax = 2560, обладает талантом, лишь слегка превышающим медианное значение mT = 0,6, в то время как самый одарённый имеет капитал / успешность ниже, чем C = 1 единице, гораздо меньше начального капитала C(0). Читайте далее для получения более подробной информации.
На рисунке 5 количество удачных и неудачных событий, произошедших со всеми людьми за период их рабочей жизни, показано в виде функции от их итоговых капитала / успешности. При рассмотрении схемы (a) становится очевидно, что самые успешные личности одновременно являются и наиболее удачливыми (обратите внимание, что на данной схеме приведены все удачные события, случившиеся с агентами, а не только те, из которых они смогли извлечь выгоду, в соответствии со своим талантом). Напротив, при взгляде на схему (b), видим, что самые неуспешные одновременно являются и наиболее неудачливыми. Другими словами, хотя корреляция между успехом и талантом, исходя из симуляций, отсутствует, зато имеется сильная зависимость успеха от удачи. Анализируя подробности распределений частот количества происходивших с индивидами удачных и неудачных событий, мы обнаружили, как это показано на схемах © и (d), что оба этих значения экспоненциальные, со степенями 0,64 и 0,48, а медианами 1,35 и 1,66, соответственно, и что максимальные количества произошедших удачных и неудачных событий были, соответственно, 10 и 15. Более того, у примерно 16% была «нейтральная» жизнь, вообще без удачных и неудачных событий, в то время как 40% индивидов сталкивались исключительно с каким-то одним типом событий (удачным или неудачным).
Также интересно взглянуть на период развития успешности / капитала как у наиболее удачливых личностей, так и для самых неуспешных, сравнив с соответствующими последовательностями удачных и неудачных событий, произошедшими в течение 40 лет (80 интервалов, по 6 месяцев каждый) их трудовой жизни. Результаты можно увидеть, соответственно, в левой и правой частях рисунка 6. В отличие от схемы (a) с изображения 5, нижние схемы данного рисунка содержат лишь те удачные события, из которых агенты, благодаря своему таланту, смогли извлечь выгоду.
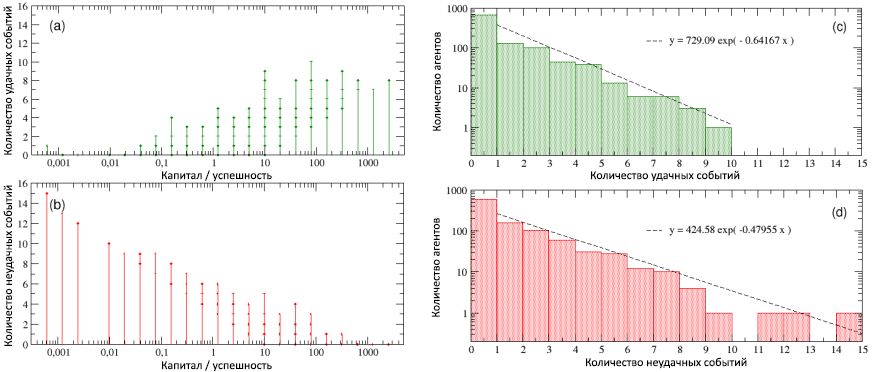
Рисунок 5: общее число удачных (a) и неудачных (b) событий, в виде функций от капитала / успешности агентов. График показывает наличие сильной корреляции между успешностью и удачей: самые успешные личности также являются наиболее удачливыми, и наоборот. Опять же, из-за использования одинакового для всех агентов начального капитала, получается, что ряд событий сгруппирован в дискретных значениях капитала / успешности. На схемах © и (d) частота распределений, соответственно, количества удачных и неудачных событий отображена в логлинейном масштабе. Как видно, оба распределения могут быть записаны в виде экспоненциальных зависимостей с похожими отрицательными степенями).
На (верхней и нижней) схемах (a) рисунка 6, касающихся умеренно талантливого, но наиболее успешного индивида, ясно видно, что после примерно половины его трудовой жизни, сопровождавшейся редким проявлением удачных событий (нижняя схема), и низким же уровнем капитала (верхняя схема), внезапная концентрация благоприятных событий, случившаяся между 30 и 40 временными шагами (т.е. прямо перед 40-летием агента) привела к стремительному росту капитала, который на последних 10 шагах (т.е., в последние 5 лет карьеры агента) стал экспоненциальным, перейдя от C = 320 до Cmax = 2560.
С другой стороны, посмотрев на (верхнюю и нижнюю) схемы (b) того же рисунка, касающиеся наименее удачливого индивида, становится очевидно, что особо неудачная вторая половина его трудовой жизни, сопровождающаяся десятком неблагоприятных событий, постоянно снижала капитал / успешность, приведя к финальному значению C = 0,00061. Интересно отметить, что талант данного несчастного агента был T = 0,74, что выше, чем у большинства самых успешных. Очевидно, на создание различий повлияла удача. И, если справедливо то, что самый удачливый агент заслуживал получения выгоды ото всех предоставленных ему возможностей (несмотря на свой посредственный талант), также верно и то, что если ваша жизнь полна несчастий и не даёт возможностей, как у этого второго агента, то даже величайший талант становится бессильным против неистовой неудачи.
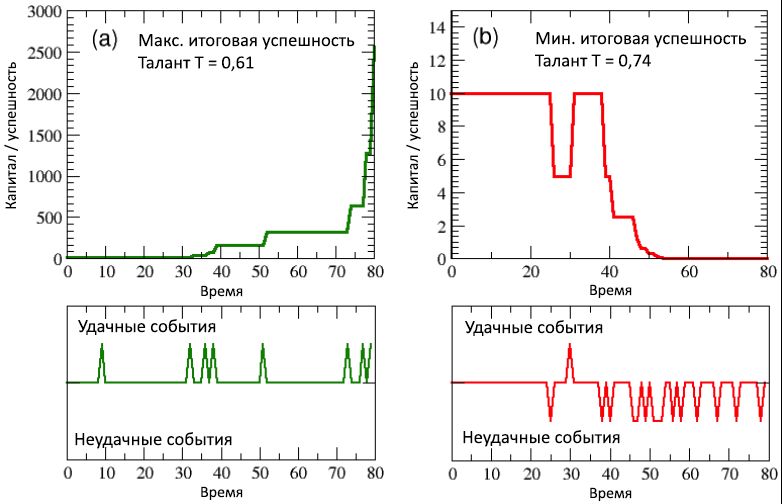
Рисунок 6: (a) период развития успешности / капитала наиболее успешного индивида и (b) самого неудачливого, сопоставленных по соответствующим последовательностям удачных и неудачных событий, произошедших в течение их трудовой жизни (из 80 полугодий, т.е., 40 лет). Время происхождения таких событий отмечено на нижних схемах, в виде восходящих и нисходящих пиков.
Все результаты одиночной прогонки (демо-версию кода NetLogo модели ТпУ, использованного для этой симуляции, можно найти в репозитории Open ABM), приведённые в данном подразделе, весьма устойчивы и, как мы увидим из следующего подраздела, они сохраняются, с незначительными отличиями, при множестве повторов симуляций, начинающихся с таким же распределением таланта, но разными случайными позициями индивидов.
2.2. Результаты множества прогонок
В данном подразделе мы представили общие результаты симуляции из, в среднем, более 100 прогонок, каждая начиналась с разными, выбранными случайным образом, исходными условиями. Значения управляющих параметров были те же, что и в предыдущем подразделе: N = 1000 индивидов, mT = 0,6 и σT = 0,1 для нормального распределения таланта, I = 80 итераций (каждая представляет δt = 6 месяцев трудовой жизни), C(0) = 10 единиц начального капитала, NE = 500 событийных точек и процент удачных событий pL = 50%.
На схеме (a) рисунка 7 общее распределение итогового капитала / успешности среди всех агентов, собранное в результате 100 прогонок, показано в билогарифмическом масштабе и оно хорошо описывается кривой степенной зависимости с угловым коэффициентом −1,33. Наблюдавшееся в одиночной прогонке свойство постоянности капитала безотносительно масштаба и следующее из него высокое неравенство среди индивидов, также как и правило Парето »80/20», таким образом, сохранились и в случае множественных прогонок. В действительности, разрыв между богатыми (успешными) и бедными (неудачливыми) агентами даже вырос, поскольку капитал наиболее богатых людей теперь превысил 40000 единиц.
Этот результат лучше всего можно оценить, взглянув на схему (b) рисунка 7, где в виде функции от таланта приведён итоговый капитал Cmax только наиболее успешных индивидов, т.е. показавших лучший результат в каждой из 100 прогонок. Больше всего очков получил агент с талантом Tbest = 0,6048, практически совпадающим с медианой распределения таланта (mT = 0,6), который достиг пикового капитала Cbest = 40960. С другой стороны, самый одарённый из наиболее успешных индивидов, с талантом Tmax = 0,91, набрал капитал Cmax = 2560, составляющий лишь 6% от Cbest.
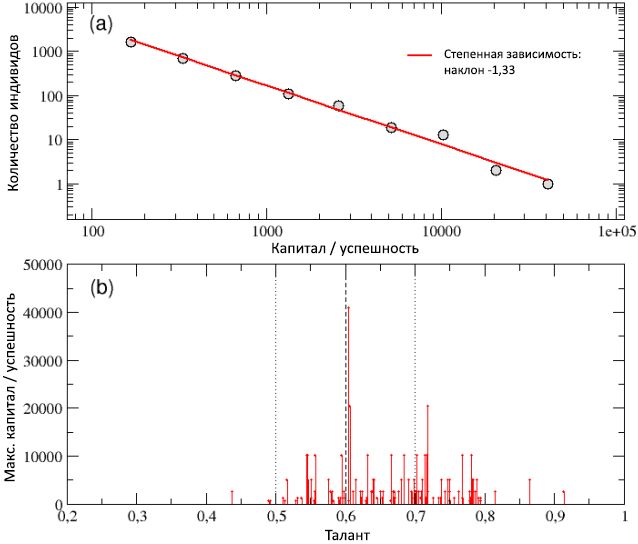
Рисунок 7: схема (a) — распределение итогового капитала / успешности, рассчитанного за 100 прогонок, для популяций, обладающими различными случайно определёнными первоначальными условиями. Распределение можно описать кривой степенной зависимости с наклоном −1,33. Схема (b) — итоговый капитал Cmax наиболее успешных личностей в каждой из 100 прогонок, показанный в виде функции от их таланта. Люди с умеренно-высоким талантом, в среднем, оказываются успешней тех, у кого талант низкий или умеренно-низкий, при этом чаще всего самый успешный индивид — это умеренно одарённый агент, и лишь изредка — самый талантливый. Значение mT, а также значения mT ± σT, показаны, соответственно, в виде вертикальных прерывистой и точечной линий.
С целью более подробного рассмотрения данной точки зрения, на рисунке 8 (а) мы построили график распределения таланта лучших исполнителей, подсчитанных за 100 прогонок. Распределение, очевидно, смещено вправо по оси таланта, со средним значением Tav = 0,66 > mT — это подтверждает, с одной стороны, что для достижения значительного успеха зачастую необходим умеренно-высокий талант; однако, с другой стороны, также показывает, что этого условия практически никогда не достаточно, так как агенты с наивысшим талантом (т.е., с T > mT = 2σT, или T > 0,8) оказываются среди лучших исполнителей лишь в 3% случаев, а их капитал / успешность никогда не превышает 13% от Cbest.
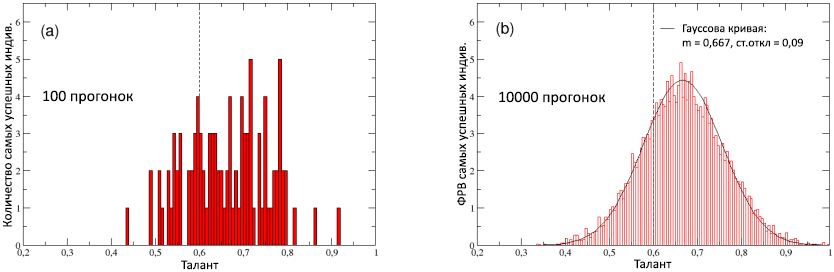
Рисунок 8: (a) Распределение таланта наиболее удачливых личностей (лучшие исполнители) в каждой из 100 прогонок. (b) Функция распределения вероятности (ФРВ) таланта самых успешных индивидов, рассчитанная в 10000 прогонок: хорошо описывается нормальным распределением с медианой 0,667 и стандартным отклонением 0,09 (сплошная кривая). Для сравнения приведена медиана mT = 0,6 исходного нормального распределения таланта в популяции, показанная на обеих схемах прерывистой вертикальной линией.
На схеме (b) рисунка 8 то же распределение (приведённое к общей площади, чтобы получить ФРП) подсчитано для 10000 прогонок, с целью понимания его истинной формы: похоже, что оно укладывается в Гауссову кривую G (T) со средним Tav = 0,667 и стандартным отклонение
