Свободу зависимым переменным
Первое апреля известно как день про белые спины и развязавшиеся шнурки. Но в университете, в котором я учился, этот день также считается днём математики. Поэтому я решил в этой хабрастатье, собрать несколько своих забавных задачек и историй, связанных в каком-то смысле с математикой.
1. Почему мне нравится ездить на верхних полках в поезде
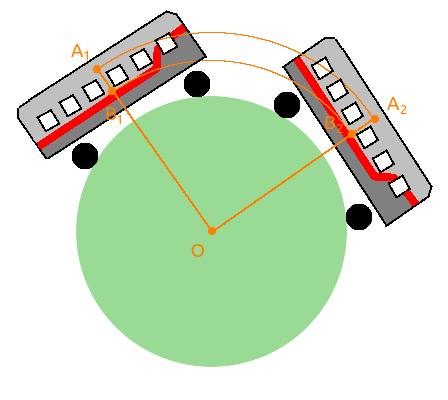
Представим, что земля это шар и мы едем c другом из Омска в Москву по дуге окружности, тогда мой друг, который едет на нижней полке, проедет путь равный длине дуги B1B2, а, я — путь равный длине дуги A1A2.Между Омском и Москвой примерно 2500 км, поэтому угол A1OA2 равен примерно 2500 / 6400 = 0,4 рад.Так как A1A2 = OA1 · 0,4, B1B2 = OB1 · 0,4, а расстояние между верхней и нижней полкой примерно 1 метр, то я проеду на A1A2 — B1B2 = (OA1 — OB1) · 0,4 = 1 · 0,4 м = 40 сантиметров больше за те же деньги.
2. Задача про моего друга Саню
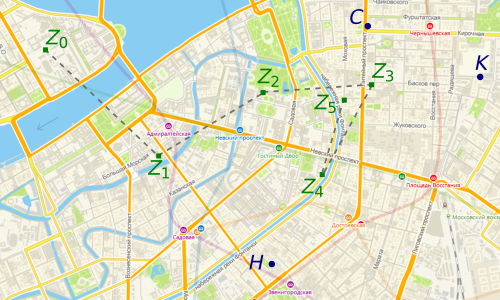
Мой друг Александр договорился о свиданиях с тремя девушками, которых звали Настя, Света и Катя, на один и тот же вечер. С Настей он договорился встретиться рядом с домом 90 к5 на Набережной реки Фонтанки, со Светой на пересечении Литейного и Кирочной, а с Катей у дома 5 на Фонтанной улице (точки Н, С и K на рис.). Александр вышел с работы на встречу с Настей, но на полпути подумал, что Света красивее, и пошёл до места встречи с ней. Пройдя половину пути до Светы он подумал, что с Катей у него больше шансов, и пошёл туда, где они договорились встретиться. Но на полпути он решил, что Настя всё-таки умнее и пошёл в сторону Насти. Где в итоге оказался мой друг, если он продолжал ходить так весь вечер?
Решение
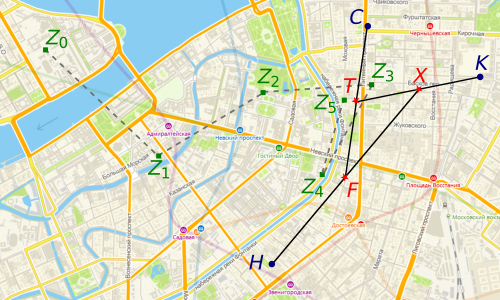
Предположим, что Саня умеет ходить сквозь стены и другие преграды. Поместим Санкт-Петербург на комплексную плоскость и пусть он работает в Z0. Тогда последовательность точек, в которых он менял решения, имеет вид: Z1 = (Z0 + H) / 2, Z2 = (Z1 + C) / 2, Z3 = (Z2 + K) / 2, Z4 = (Z3 + H) / 2, … Разобъём эту последовательность на три подпоследовательности: Z0, Z3, Z6, Z9, …; Z1, Z4, Z7, Z10, … и Z2, Z5, Z8, Z11, … Пусть f (Z) = (((Z + H) / 2 + C) / 2 + K) / 2. Тогда первая подпоследовательность запишется в виде Z0, f (Z0), f (f (Z0)), f (f (f (Z0))), … Заметим, что отображение f является сжимающим, следовательно, по теореме Банаха о неподвижной точке существует единственная неподвижная точка этого отображения, обозначим её X. При этом эта подпоследовательность сходится к этой точке. Для других двух подпоследовательностей по аналогичным соображениям также существуют неподвижные точки, которые обозначим F и T соответственно. Эти точки соответствуют адресам: Некрасова, 26, Рубинштейна, 5 и Белинского, 11 (см. рис.). По первому адресу находится бар Хроники, по второму — бар Fiddler’s Green, по третьему — Terminal. Таким образом, остаток дня Александр проведёт в этих барах, переходя по очереди из одного в другой.
3. Учимся везде видеть данные
Если выйти на улицу, то можно заметить на столбах и стенах домов много бумажек с парами, первый элемент которых — женское имя, а второй элемент — некоторая последовательность цифр. Примеры приведены ниже.
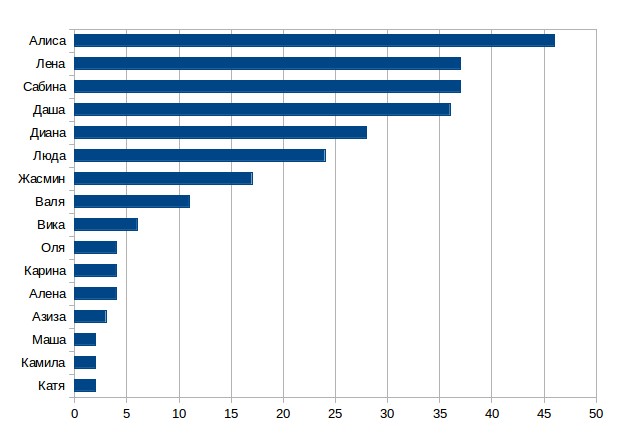
Совсем не интересуясь вторыми элементами этих пар, посмотрим, какое распределение у первых элементов.
Для этого я как-то в августе прошёл километров шесть по улице и собрал статистику.
Было обработано 263 объявления, TOP-5 имён выглядит так: Алиса, Лена, Сабина, Даша, Диана:
4. Задача про моего друга Костю
Мой друг Константин каждый вечер в 7 часов выходит с работы и идёт до метро. Там он случайно выбирает ветку и направление, садится на поезд, проезжает одну станцию, затем снова случайно выбирает ветку и направление, снова проезжает одну станцию, и так далее, пока не доедет до дома. Зная, что Костя работает на Льва Толстого, а живёт около ст. м. Беляево, определите, как часто он пьёт пиво, если он покупает пиво в магазине рядом с домом после работы.
Решение
Московскому метрополитену можно сопоставить марковскую цепь с матрицей P (см. рис.). И, так как Костя выходит на ст. м. Беляево, то это состояние Б будет поглощающим.
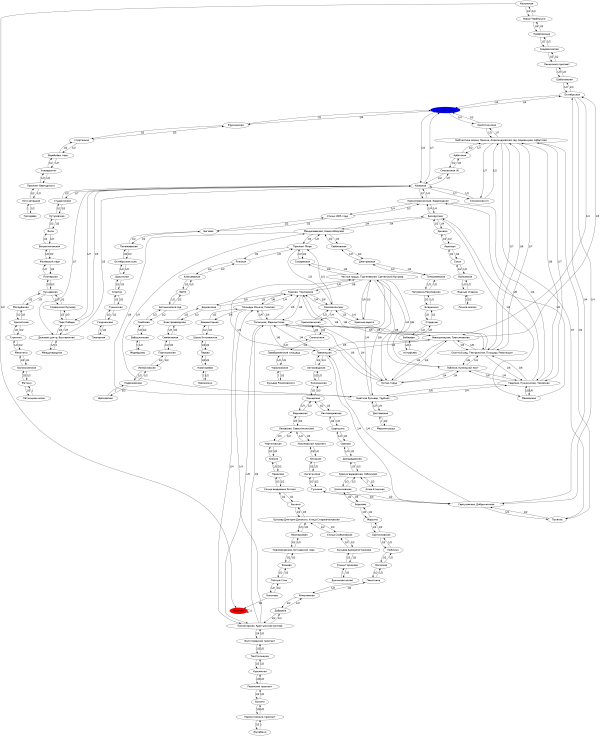(Нажмите по картинке для увеличения.)
Далее, предположим, что на один перегон затрачивается примерно три минуты. Так как в Москве перестают продавать пиво в 23:00, и (23:00 — 19:00) / 3 мин. = 80, то нам нужно найти вероятность оказаться в состоянии Б менее чем за 80 шагов. Несложно понять, что для нахождения этой вероятности нужно возвести матрицу P в степень 79 и взять элемент на пересечении строки, которая соответствует Парку культуры, и столбца, который соответствует Беляево. Рассчёты показывают (см. рис. ниже), что искомая вероятность примерно равна 5,9%. Следовательно, мой друг пьёт пиво примерно раз в 17 дней.
5. Чипсоиды
Некоторое время назад в интернете гуляла картинка с фактом о том, что чипсина Принглс является гиперболическим параболоидом:
Когда я её увидел, я сказал себе: «Ага! А так как гиперболический параболоид является линейчатой поверхностью, то чипсина должна пролезать через прямолинейную щель». Поэтому я купил на следующий день чипсов, прорезал в картонке щель и проделал этот эксперимент:
[embedded content]
Ещё одним примером линейчатой поверхности является однополостный гиперболоид. Проверить этот факт можно с помощью бутылки из-под йогурта Чудо. Берём бутылку из-под йогурта, вырезаем часть бутылки, которая является чем-то похожим на однополостный гиперболоид, снова вырезаем в листе картона щель, вставляем кусок бутылки в щель и крутим:
[embedded content]
Удачного дня!
