SVM. Объяснение с нуля, имплементация и подробный разбор
Привет всем, кто выбрал путь ML-самурая!
Введение:
В данной статье рассмотрим метод опорных векторов (англ. SVM, Support Vector Machine) для задачи классификации. Будет представлена основная идея алгоритма, вывод настройки его весов и разобрана простая реализация своими руками. На примере датасета будет продемонстрирована работа написанного алгоритма с линейно разделимыми/неразделимыми данными в пространстве
и визуализация обучения/прогноза. Дополнительно будут озвучены плюсы и минусы алгоритма, его модификации.

Рисунок 1. Фото цветка ириса из открытых источников
Решаемая задача:
Будем решать задачу бинарной (когда класса всего два) классификации. Сначала алгоритм тренируется на объектах из обучающей выборки, для которых заранее известны метки классов. Далее уже обученный алгоритм предсказывает метку класса для каждого объекта из отложенной/тестовой выборки. Метки классов могут принимать значения . Объект — вектор c N признаками
в пространстве
. При обучении алгоритм должен построить функцию
, которая принимает в себя аргумент
— объект из пространства
и выдает метку класса
.
Общие слова об алгоритме:
Задача классификация относится к обучению с учителем. SVM — алгоритм обучения с учителем. Наглядно многие алгоритмы машинного обучения можно посмотреть в этой топовой статье (см. раздел «Карта мира машинного обучения»). Нужно добавить, что SVM может применяться и для задач регрессии, но в данной статье будет разобран SVM-классификатор.
Главная цель SVM как классификатора — найти уравнение разделяющей гиперплоскости в пространстве
, которая бы разделила два класса неким оптимальным образом. Общий вид преобразования
объекта
в метку класса
:
. Будем помнить, что мы обозначили
. После настройки весов алгоритма
и
(обучения), все объекты, попадающие по одну сторону от построенной гиперплоскости, будут предсказываться как первый класс, а объекты, попадающие по другую сторону — второй класс.
Внутри функции стоит линейная комбинация признаков объекта с весами алгоритма, именно поэтому SVM относится к линейным алгоритмам. Разделяющую гиперплоскость можно построить разными способами, но в SVM веса
и
настраиваются таким образом, чтобы объекты классов лежали как можно дальше от разделяющей гиперплоскости. Другими словами, алгоритм максимизирует зазор (англ. margin) между гиперплоскостью и объектами классов, которые расположены ближе всего ней. Такие объекты и называют опорными векторами (см. рис. 2). Отсюда и название алгоритма.

Рисунок 2. SVM (основа рисунка отсюда)
Подробный вывод правил настройки весов SVM:
Чтобы разделяющая гиперплоскость как можно дальше отстояла от точек выборки, ширина полосы должна быть максимальной. Вектор — направляющий вектор разделяющей гиперплоскости. Здесь и далее будем обозначать скалярное произведение двух векторов как
или
.Давайте найдем проекцию вектора, концами которого будут являться опорные вектора разных классов на направляющий вектор гиперплоскости. Эта проекция и будет показывать ширину разделяющий полосы (см. рис. 3):

Рисунок 3. Вывод правил настройки весов (основа рисунка отсюда)
Отступом (англ. margin) объекта x от границы классов называется величина . Алгоритм допускает ошибку на объекте тогда и только тогда, когда отступ
отрицателен (когда
и
разных знаков). Если
, то объект попадает внутрь разделяющей полосы. Если $inline$M > 1$inline$, то объект x классифицируется правильно, и находится на некотором удалении от разделяющей полосы. Запишем и эту связь:
Получаемая система является дефолтной настройкой SVM с жестким зазором (hard-margin SVM), когда никакому объекту не разрешается попадать на полосу разделения. Решается аналитически через теорему Куна-Таккера. Получаемая задача эквивалентна двойственной задаче поиска седловой точки функции Лагранжа.
$$display$$ \left\{ \begin{array}{ll} (w^Tw)/2 \rightarrow min & \textrm{}\\ y (w^Tx-b) \geqslant 1 & \textrm{} \end{array} \right. $$display$$
Всё это хорошо до тех пор, пока у нас классы линейно разделимы. Чтобы алгоритм смог работать и с линейно неразделимых данными, давайте немного преобразуем нашу систему. Позволим алгоритму допускать ошибки на обучающих объектах, но при этом постараемся, чтобы ошибок было поменьше. Введём набор дополнительных переменных $inline$\xi _i > 0$inline$, характеризующих величину ошибки на каждом объекте . Введём в минимизируемый функционал штраф за суммарную ошибку:
$$display$$ \left\{ \begin{array}{ll} (w^Tw)/2 + \alpha\sum\xi _i \rightarrow min & \textrm{}\\ y (w^Tx_i-b) \geqslant 1 -\xi _i & \textrm{}\\ \xi _i\geqslant0& \textrm{} \end{array} \right. $$display$$
Будем считать количество ошибок алгоритма (когда M<0). Назовем это штрафом (Penalty). Тогда штраф для всех объектов будет равен сумме штрафов для каждого объекта , где $inline$[M_i<0]$inline$ — пороговая функция (см. рис.4):
$$display$$Penalty = \sum[M_i < 0]$$display$$
$$display$$ [M_i < 0] = \left\{ \begin{array}{ll} 1 & \textrm{, если }M_i < 0\\ 0 & \textrm{, если }M_i\geqslant 0 \end{array} \right. $$display$$
Далее сделаем штраф чувствительным к величине ошибки и заодно введем штраф за приближение объекта к границе классов:
$$display$$Penalty = \sum[M_i < 0] \leqslant \sum(1- M_i)_+ = \sum max(0,1-M_i)$$display$$
При добавлении к выражению штрафа слагаемое получаем классическую фукцию потерь SVM с мягким зазором (soft-margin SVM) для одного объекта:
— функция потерь, она же loss function. Именно ее мы и будем минимизировать с помощью градиентного спуска в реализации руками. Выведем правила изменения весов, где
— шаг спуска:
$$display$$ \bigtriangledown Q = \left\{ \begin{array}{ll} \alpha w-yx & \textrm{, если }yw^Tx<1\\ \alpha w & \textrm{, если }yw^Tx\geqslant 1 \end{array} \right. $$display$$
Возможные вопросы на собеседованиях (основано на реальных событиях):
После общих вопросов про SVM: Почему именно Hinge_loss максимизирует зазор? — для начала вспомним, что гиперплоскость меняет свое положение тогда, когда изменяются веса и
. Веса алгоритма начинают меняться, когда градиенты лосс-функции не равны нулю (обычно говорят: «градиенты текут»). Поэтому мы специально подобрали такую лосс-функцию, у которой начинают течь градиенты в нужное время.
выглядит следующим образом:
. Помним, что зазор
. Когда зазор
достаточно большой (
или более), выражение
становится меньше нуля и
(поэтому градиенты не текут и веса алгоритма никак не изменяются). Если же зазор m достаточно малый (например, когда объект попадает на полосу разделения и/или отрицательный (при неверном прогнозе классификации), то Hinge_loss становится положительной ($inline$H>0$inline$), начинают течь градиенты и веса алгоритма изменяются. Резюмируя: градиенты текут в двух случаях: когда объект выборки попал внутрь полосы разделения и при неправильной классификации объекта.
Для проверки уровня иностранного языка возможны подобные вопросы: What are the similarities and differences between LogisticRegression and SVM? — firstly, we will talk about similarities: both of algorithms are linear classification algorithms in supervised learning. Some similarities are in their arguments of loss functions: for LogReg and
for SVM (look at picture 4). Both of algorithms we can configure using gradient descent. Next let«s talk about differences: SVM return class label of object unlike LogReg, which return probability of class membership. SVM can«t work with class labels
(without renaming classes) unlike LogReg (LogReg loss finction for
:
, where
— real class label,
— algorithm«s return, probability of belonging object
to class
). More than that, we can solve hard-margin SVM problem without gradient descent. The task of searching support vectors is reduced to search saddle point in the Lagrange function — this task refers to quadratic programming only.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
xx = np.linspace(-4,3,100000)
plt.plot(xx, [(x<0).astype(int) for x in xx], linewidth=2, label='1 if M<0, else 0')
plt.plot(xx, [np.log2(1+2.76**(-x)) for x in xx], linewidth=4, label='logistic = log(1+e^-M)')
plt.plot(xx, [np.max(np.array([0,1-x])) for x in xx], linewidth=4, label='hinge = max(0,1-M)')
plt.title('Loss = F(Margin)')
plt.grid()
plt.legend(prop={'size': 14});
Риcунок 4. Функции потерь
Простая имплементация классического soft-margin SVM:
Внимание! Ссылку на полный код вы найдете в конце статьи. Ниже будут представлены блоки кода, вырванные из контекста. Некоторые блоки можно запускать только после отработки предыдущих блоков. Под многими блоками будут размещены картинки, которые показывают, как отработал код, размещенный над ней.
import numpy as np
import warnings
warnings.filterwarnings('ignore')
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
plt.rcParams['figure.figsize'] = (8,6)
%matplotlib inline
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
def newline(p1, p2, color=None): # функция отрисовки линии
#function kredits to: https://fooobar.com/questions/626491/how-to-draw-a-line-with-matplotlib
ax = plt.gca()
xmin, xmax = ax.get_xbound()
if(p2[0] == p1[0]):
xmin = xmax = p1[0]
ymin, ymax = ax.get_ybound()
else:
ymax = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmax-p1[0])
ymin = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmin-p1[0])
l = mlines.Line2D([xmin,xmax], [ymin,ymax], color=color)
ax.add_line(l)
return ldef add_bias_feature(a):
a_extended = np.zeros((a.shape[0],a.shape[1]+1))
a_extended[:,:-1] = a
a_extended[:,-1] = int(1)
return a_extended
class CustomSVM(object):
__class__ = "CustomSVM"
__doc__ = """
This is an implementation of the SVM classification algorithm
Note that it works only for binary classification
#############################################################
###################### PARAMETERS ######################
#############################################################
etha: float(default - 0.01)
Learning rate, gradient step
alpha: float, (default - 0.1)
Regularization parameter in 0.5*alpha*||w||^2
epochs: int, (default - 200)
Number of epochs of training
#############################################################
#############################################################
#############################################################
"""
def __init__(self, etha=0.01, alpha=0.1, epochs=200):
self._epochs = epochs
self._etha = etha
self._alpha = alpha
self._w = None
self.history_w = []
self.train_errors = None
self.val_errors = None
self.train_loss = None
self.val_loss = None
def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1
if len(set(Y_train)) != 2 or len(set(Y_val)) != 2:
raise ValueError("Number of classes in Y is not equal 2!")
X_train = add_bias_feature(X_train)
X_val = add_bias_feature(X_val)
self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1])
self.history_w.append(self._w)
train_errors = []
val_errors = []
train_loss_epoch = []
val_loss_epoch = []
for epoch in range(self._epochs):
tr_err = 0
val_err = 0
tr_loss = 0
val_loss = 0
for i,x in enumerate(X_train):
margin = Y_train[i]*np.dot(self._w,X_train[i])
if margin >= 1: # классифицируем верно
self._w = self._w - self._etha*self._alpha*self._w/self._epochs
tr_loss += self.soft_margin_loss(X_train[i],Y_train[i])
else: # классифицируем неверно или попадаем на полосу разделения при 0 np.array:
y_pred = []
X_extended = add_bias_feature(X)
for i in range(len(X_extended)):
y_pred.append(np.sign(np.dot(self._w,X_extended[i])))
return np.array(y_pred)
def hinge_loss(self, x, y):
return max(0,1 - y*np.dot(x, self._w))
def soft_margin_loss(self, x, y):
return self.hinge_loss(x,y)+self._alpha*np.dot(self._w, self._w) Подробно рассмотрим работу каждого блока строчек:
1) создаем функцию add_bias_feature (a), которая автоматически расширяет вектор объектов, добавляя в конец каждого вектора число 1. Это нужно для того, чтобы «забыть» про свободный член b. Выражение эквивалентно выражению
. Мы условно считаем, что единица — это последняя компонента вектора для всех векторов x, а
. Теперь настройку весов
и
будем производить одновременно.
def add_bias_feature(a):
a_extended = np.zeros((a.shape[0],a.shape[1]+1))
a_extended[:,:-1] = a
a_extended[:,-1] = int(1)
return a_extended2) далее опишем сам классификатор. Он имеет внутри себя функции инициализации init (), обучения fit (), предсказания predict (), нахождения лосс функции hinge_loss () и нахождения общей лосс функции классического алгоритма с мягким зазором soft_margin_loss ().
3) при инициализации вводятся 3 гиперпараметра: _etha — шаг градиентного спуска (), _alpha — коэффициент быстроты пропорционального уменьшения весов (перед квадратичным слагаемым в функции потерь
), _epochs — количество эпох обучения.
def __init__(self, etha=0.01, alpha=0.1, epochs=200):
self._epochs = epochs
self._etha = etha
self._alpha = alpha
self._w = None
self.history_w = []
self.train_errors = None
self.val_errors = None
self.train_loss = None
self.val_loss = None4) при обучении для каждой эпохи обучающей выборки (X_train, Y_train) мы будем брать по одному элементу из выборки, вычислять зазор между этим элементом и положением гиперплоскости в данный момент времени. Далее в зависимости от величины этого зазора мы будем изменять веса алгоритма с помощью градиента функции потерь . Заодно будем вычислять значение этой функции на каждой эпохе и сколько раз мы изменяем веса за эпоху. Перед началом обучения убедимся, что в функцию обучения пришло действительно не больше двух разных меток класса. Перед настройкой весов происходит их инициализация с помощью нормального распределения.
def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1
if len(set(Y_train)) != 2 or len(set(Y_val)) != 2:
raise ValueError("Number of classes in Y is not equal 2!")
X_train = add_bias_feature(X_train)
X_val = add_bias_feature(X_val)
self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1])
self.history_w.append(self._w)
train_errors = []
val_errors = []
train_loss_epoch = []
val_loss_epoch = []
for epoch in range(self._epochs):
tr_err = 0
val_err = 0
tr_loss = 0
val_loss = 0
for i,x in enumerate(X_train):
margin = Y_train[i]*np.dot(self._w,X_train[i])
if margin >= 1: # классифицируем верно
self._w = self._w - self._etha*self._alpha*self._w/self._epochs
tr_loss += self.soft_margin_loss(X_train[i],Y_train[i])
else: # классифицируем неверно или попадаем на полосу разделения при 0Проверка работы написанного алгоритма:
Проверим, что наш написанный алгоритм работает на каком-нибудь игрушечном наборе данных. Возьмем датасет Iris. Подготовим данные. Обозначим классы 1 и 2 как , а класс 0 как
. С помощью алгоритма PCA (объяснение и применение тут) оптимальным образом сократим пространство 4-х признаков до 2-х с минимальными потерями данных (нам будет проще наблюдать за обучением и разультатом). Далее разделим на обучающую (трейн) выборку и отложенную (валидационную). Обучим на трейн выборке, прогнозируем и проверяем на отложенной. Подберем коэффициенты обучения таким образом, чтобы лосс функция падала. Во время обучения будем смотреть на лосс функцию обучающей и отложенной выборки.
# блок подготовки данных
iris = load_iris()
X = iris.data
Y = iris.target
pca = PCA(n_components=2)
X = pca.fit_transform(X)
Y = (Y > 0).astype(int)*2-1 # [0,1,2] --> [False,True,True] --> [0,1,1] --> [0,2,2] --> [-1,1,1]
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020)# блок инициализиции и обучения
svm = CustomSVM(etha=0.005, alpha=0.006, epochs=150)
svm.fit(X_train, Y_train, X_test, Y_test)
print(svm.train_errors) # numbers of error in each epoch
print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0
plt.plot(svm.train_loss, linewidth=2, label='train_loss')
plt.plot(svm.val_loss, linewidth=2, label='test_loss')
plt.grid()
plt.legend(prop={'size': 15})
plt.show()
d = {-1:'green', 1:'red'}
plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train])
newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') # в w0*x_i[0]+w1*x_i[1]+w2*1=0 поочередно
# подставляем x_i[0]=0, x_i[1]=0
newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1
newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1
plt.show()
# предсказываем после обучения
y_pred = svm.predict(X_test)
y_pred[y_pred != Y_test] = -100 # find and mark classification error
print('Количество ошибок для отложенной выборки: ', (y_pred == -100).astype(int).sum())
d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error
plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred])
newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue')
newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1
newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1
plt.show()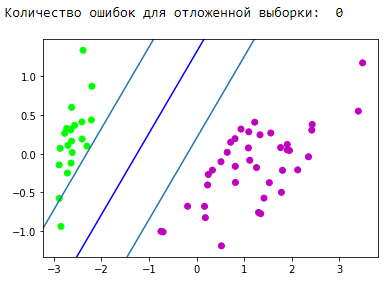
Отлично! Наш алгоритм справился с линейно разделимыми данными. Теперь заставим его отделить классы 0 и 1 от класса 2:
# блок подготовки данных
iris = load_iris()
X = iris.data
Y = iris.target
pca = PCA(n_components=2)
X = pca.fit_transform(X)
Y = (Y == 2).astype(int)*2-1 # [0,1,2] --> [False,False,True] --> [0,1,1] --> [0,0,2] --> [-1,1,1]
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020)# блок инициализиции и обучения
svm = CustomSVM(etha=0.03, alpha=0.0001, epochs=300)
svm.fit(X_train, Y_train, X_test, Y_test)
print(svm.train_errors[:150]) # numbers of error in each epoch
print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0
plt.plot(svm.train_loss, linewidth=2, label='train_loss')
plt.plot(svm.val_loss, linewidth=2, label='test_loss')
plt.grid()
plt.legend(prop={'size': 15})
plt.show()
d = {-1:'green', 1:'red'}
plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train])
newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') # в w0*x_i[0]+w1*x_i[1]+w2*1=0 поочередно
# подставляем x_i[0]=0, x_i[1]=0
newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1
newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1
plt.show()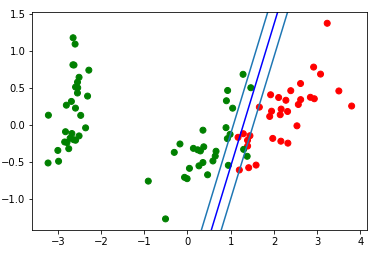
Посмотрим на гифку, которая покажет, как разделяющая прямая изменяла свое положение во время обучения (всего 500 кадров изменения весов. Первые 300 подряд. Далее 200 штук на каждый 130ый кадр):
import matplotlib.animation as animation
from matplotlib.animation import PillowWriter
def one_image(w, X, Y):
axes = plt.gca()
axes.set_xlim([-4,4])
axes.set_ylim([-1.5,1.5])
d1 = {-1:'green', 1:'red'}
im = plt.scatter(X[:,0], X[:,1], c=[d1[y] for y in Y])
im = newline([0,-w[2]/w[1]],[-w[2]/w[0],0], 'blue')
# im = newline([0,1/w[1]-w[2]/w[1]],[1/w[0]-w[2]/w[0],0], 'lime') #w0*x_i[0]+w1*x_i[1]+w2*1=1
# im = newline([0,-1/w[1]-w[2]/w[1]],[-1/w[0]-w[2]/w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1
return im
fig = plt.figure()
ims = []
for i in range(500):
if i<=300:
k = i
else:
k = (i-298)*130
im = one_image(svm.history_w[k], X_train, Y_train)
ims.append([im])
ani = animation.ArtistAnimation(fig, ims, interval=20, blit=True,
repeat_delay=500)
writer = PillowWriter(fps=20)
ani.save("my_demo.gif", writer='imagemagick')
# предсказываем после обучения
y_pred = svm.predict(X_test)
y_pred[y_pred != Y_test] = -100 # find and mark classification error
print('Количество ошибок для отложенной выборки: ', (y_pred == -100).astype(int).sum())
d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error
plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred])
newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue')
newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1
newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1
plt.show()
Спрямляющие пространства
Важно понимать, что в реальных задачах не будет простого случая с линейно разделимыми данными. Для работы с подобными данными была предложена идея перехода в другое пространство, где данные будут линейно разделимы. Такое пространство и называется спрямляющим. В данной статье не будут затронуты спрямляющие пространства и ядра. Самую полную математическую теорию Вы сможете найти в 14,15,16 конспектах Е. Соколова и в лекциях К.В. Воронцова.
Применение SVM из sklearn:
В действительности, почти все классические алгоритмы машинного обучения написаны за Вас. Приведем пример кода, алгоритм возьмем из библиотеки sklearn.
from sklearn import svm
from sklearn.metrics import recall_score
C = 1.0 # = self._alpha in our algorithm
model1 = svm.SVC(kernel='linear', C=C)
#model1 = svm.LinearSVC(C=C, max_iter=10000)
#model1 = svm.SVC(kernel='rbf', gamma=0.7, C=C)
#model1 = svm.SVC(kernel='poly', degree=3, gamma='auto', C=C)
model1.fit(X_train, Y_train)
y_predict = model1.predict(X_test)
print(recall_score(Y_test, y_predict, average=None))Плюсы и минусы классического SVM:
Плюсы:
- хорошо работает с пространством признаков большого размера;
- хорошо работает с данными небольшого объема;
- так алгоритм находит максимизирует разделяющую полосу, которая, как подушка безопасности, позволяет уменьшить количество ошибок классификации;
- так как алгоритм сводится к решению задачи квадратичного программирования в выпуклой области, то такая задача всегда имеет единственное решение (разделяющая гиперплоскость с определенными гиперпараметрами алгоритма всегда одна).
Минусы:
- долгое время обучения (для больших наборов данных);
- неустойчивость к шуму: выбросы в обучающих данных становятся опорными объектами-нарушителями и напрямую влияют на построение разделяющей гиперплоскости;
- не описаны общие методы построения ядер и спрямляющих пространств, наиболее подходящих для конкретной задачи в случае линейной неразделимости классов. Подбирать полезные преобразования данных — искусство.
Применение SVM:
Выбор того или иного алгоритма машинного обучения напрямую зависит от информации, полученной во время исследования данных. Но в общих словах, можно выделить следующие задачи:
- задачи с небольшим набором данных;
- задачи текстовой классификации. SVM дает неплохой baseline ([preprocessing] + [TF-iDF] + [SVM]), получаемая точность прогноза оказывается на уровне некоторых сверточных/рекуррентных нейронных сетей (рекомендую самостоятельно попробовать такой метод для закрепления материала). Отличный пример приведен тут, «Часть 3. Пример одного из трюков, которым мы обучаем»;
- для многих задач со структурированными данными связка [feature engineering] + [SVM] + [kernel] «все еще торт»;
- так как Hinge loss считается довольно быстро, ее можно встретить в Vowpal Wabbit (по умолчанию).
Модификации алгоритма:
Существуют различные дополнения и модификации метода опорных векторов, направленные на устранение определенных недостатков:
- Метод релевантных векторов (Relevance Vector Machine, RVM)
- 1-norm SVM (LASSO SVM)
- Doubly Regularized SVM (ElasticNet SVM)
- Support Features Machine (SFM)
- Relevance Features Machine (RFM)
Дополнительные источники на тему SVM:
- Текстовые лекции К.В. Воронцова
- Конспекты Е.Соколова — 14,15,16
- На хабре есть 2 статьи, посвященные svm:
- На гитхабе могу выделить 2 крутые реализации SVM по следующим ссылкам:
Заключение:
Большое спасибо за внимание! Буду благодарен за любые комментарии, отзывы и советы.
Полный код из данной статьи найдете на моем гитхабе.
p.s. Благодарю yorko за советы по сглаживанию «углов». Спасибо Алексею Сизых — физтеху, который частично вложился в код.
