Суперскалярный стековый процессор: подробности

Продолжение серии статей, разбирающих идею суперскалярного процессора с OoO и фронтендом стековой машины.
Тема данной статьи — вызов функций, вид изнутри.
Предыдущие статьи:
1 — описание работы на линейном куске
2 — вызов функций, сохраняем регистры
Сосредоточившись в прошлой статье на внешней стороне вызова функций мы упустили из вида то, как всё это будет исполняться внутри. Автор не считает себя специалистом по «железу», но проблемы всё же предвидит.
Мы упоминали о том, что после возврата из функции хочется получить процессор в том же состоянии что и до него. И именно для этого озаботились сохранением состояния регистров. Но ведь состояние процессора это не только регистры., но и очереди мопов, состояние конвейеров …
Представим себе ситуацию, когда на момент вызова функции мы имеем:
- некоторое к-во мопов в стеке декодера
- мопы, удаленные декодером из стека, но ожидающие исполнения родительских мопов
- мопы на исполнении в конвейерах
В результате нельзя просто так начать исполнение новой функции т.к.
- для этого может банально не хватить мопов — те, что остались от родительской функции не освободятся пока мы не вернемся из этой
- стек индексов мопов в декодере имеет фиксированную глубину и запросто может переполниться при рекурсии или просто длинной цепочке вызовов
- мопы в конвейерах исполнятся уже после того, как (после вызова новой функции) сменится нумерация регистров
Может показаться, что мы предприняли определенные меры, чтобы избежать описанных проблем когда декларировали вызов функции обобщенной инструкцией, которая должна перед вызовом дождаться вычисления всех своих аргументов.
Однако, есть проблема с тем, что декодер успеет обработать код после вызова функции, если он независим по данным. Например:
int i, j, k;
…
i = foo (i + 1);
j += k;
bar (i, j);
После возврата из foo мы не можем полагаться ни на то, что j успела вычислиться и сохранена (а потом восстановлена) в контексте текущей задачи, ни на то, что сохранились мопы от j += k; если вычислиться она не успела.
Допустим, увидев вызов функции декодер прекращает свою работу вплоть до возврата из этой функции. Тогда как быть с такой ситуацией:
int i, j, k;
…
bar (foo (i + 1), j += k);
Одним декодером здесь не обойдешься. Похоже, после возврата из функции надо просто начинать декодирование и исполнение дальнейшего кода заново.
Но ведь в основном, эти проблемы, вызванные суперскалярностью, не уникальны для нашей архитектуры, может не нужно изобретать велосипед, а стоит посмотреть как это уже решено ранее.
Хорошо, давайте взглянем на Sandy Bridge от Intel (спасибо Таситу Мурки aka Felid)
а также здесь
Sandy Bridge.
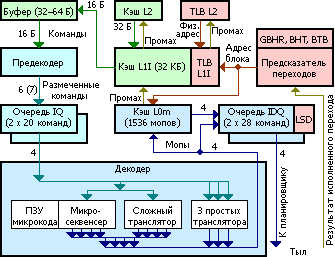
Предположительно, фронтенд Sandy Bridge,
- исполняемый код поступает в буфер предекодера (в левом верхнем углу схемы) из кэша инструкций первого уровня (L1I)
- предекодер умеет обрабатывать до 7 инструкций за такт в зависимости от их совокупной длины и сложности
- размеченные команды попадают в одну из двух очередей (IQ) команд — по одной на поток (hyperthreading), на 20 команд каждая
- декодер попеременно читает команды из очередей и переводит их в мопы
- в зависимости от типа команды, декодер использует разные типы трансляторов
- результат декодирования поступает в кэш мопов и два буфера мопов (hyperthreading)
- кэшируются выровненные куски (порции) по 32 байта исходного кода, при этом:
- ключом является точка входа в порцию, если в одну порцию были переходы в разные места, эта порция будет размножена в кэше
- декодирование порции начинается с её точки входа
- кэшируются только порции, которые породили не более 18 мопов — 3 строки по 6 мопов
- инструкция, разделенная границей двух порций, относится к первой из них
- из порции разрешено иметь не более 6 переходов, только один из них может быть безусловным — и последним одновременно. Это важно т.к. вызов функции — безусловный переход и всё что происходит после него не попадет в текущую единицу кэширования, а значит и не будет исполняться до тех пор, пока мы не попытаемся вернуться назад.
- если порция не заканчивается безусловным переходом, происходит переход на первую инструкцию следующей по адресу секции
- кэш мопов (L0m) синхронизирован с L1I, в последнем строка кэша — 64 байта, так что при вытеснении строки L1I, из L0m удаляется всё что касается двух порций
- просто любопытно, L1I работает с физическими адресами, L0m — с виртуальными
- Что касается спекулятивного исполнения:
- предсказатель переходов (BPU) умеет для мопа условного перехода сообщать вероятность наступления события этого перехода
- т.к. в текущей очереди мопов декодер уже выявил все потенциальные переходы, можно их проверить
- если вероятность перехода достаточно высокая, есть смысл заранее загрузить нужную порцию кода и спекулятивно его исполнить
- если переход действительно произойдет, мы получим как минимум декодированную порцию данных, возможно, часть инструкций (у которых нет зависимостей по данным) успеет выполниться
- если перехода не будет, инструкции, которые еще не успели исполниться следует снять с исполнения, те, что успели отработать, не должны нанести непоправимых последствий. Освобождаются все захваченные ресурсы.
- а значит, исполняться они будут в особом спекулятивном режиме:
- запись в память должна быть отложена
- чтение из памяти осуществляется только если данные уже есть в кэше данных, иначе исполнение блокируется (с целью избежать бесполезных промахов кэша и последующего обращения к свопу)
- всё, что может вызвать исключение (деление на 0, например), помечается соответствующим образом и также блокируется, впрочем, это обобщение предыдущего пункта. Теперь при наступлении перехода мы можем честно рестартовать заблокированные мопы
- и, конечно, стоит напомнить, что всё это лишь предположения, реальную картину знает только Интел
Как же происходит вызов функции?
Разберем следующий пример
int i, j, k, l, m, n;
...
i = 1 + foo (1 + bar (1 + biz (1 + baz (1 + j) + k) + l) + m) + n;
Будем наивно предполагать, что весь этот код разместится в одну 32 байтовую порцию и порядок генерации кода (при отключенном оптимизаторе) будет соответствовать порядку текста. Разметим код в соответствии с тем, в какой экземпляр секции он попадет в кэше L0m:
int i, j, k, l, m, n;
...
1> i = 1 +
4> foo (
1> 1 +
3> bar (
1> 1 +
2> biz (
1> 1 +
1> baz (1 + j)
2> + k)
3> + l)
4> + m)
5> + n;
Этот фрагмент займет по видимому 5 строк кэша из 256 имеющихся.
Неудивительно, что компилятор изо всех сил старается инлайнить небольшие функции.
Выводы
Итак, мы рассмотрели как вызываются функции в одной из весьма изощренных микро-архитектур, какую пользу можно из этого извлечь?
Выделим объективные моменты:
- Кэш инструкций нужен, без этого никакой внятный процессор невозможен.
- Кэш имеет гранулярность, на данный момент типичный размер — строка в 64 байта.
- Декодирование (для x86_64, по крайней мере)- довольно дорогая операция, есть смысл кэшировать декодированный код в виде строк мопов
- Доступ по точке входа — отличная идея, можно ли при этом обойтись без размножения записей — вопрос реализации
- Не больше одного обязательного выхода — простое и естественное решение, избавляющее от кучи проблем
Может показаться, что всё это сработает и для нашей архитектуры со стековым фронтендом. Но есть нюанс.
Поясним на примере. Вот функция Аккермана:
int a(int m, int n)
{
if (m == 0)
return n + 1;
if (n == 0)
return a(m - 1, 1);
return a(m - 1, a(m, n - 1));
}
Выглядит просто, но демонстрирует чудеса рекурсии. Нижеследующий график показывает динамику глубины вложенности для вызова a (3, 5), по x — номер шага, по y — глубина вызова.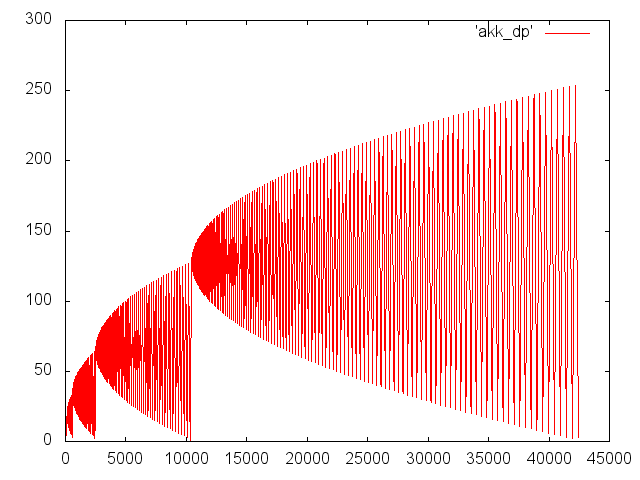
Поскольку мы решили рассматривать вызов функции как обобщенную инструкцию с произвольным количеством параметров, в случае m*n!= 0, первый аргумент (m-1) останется в стеке мопов, в то время как будет вычисляться второй аргумент: a (m, n-1). Хорошо, если первый аргумент успеет вычислиться и его значение будет сохранено при вызове в регистровом стеке. Но может так случиться, что выражение для первого аргумента будет вычисляться дольше, чем аргументы дочернего вызова во втором аргументе. И тогда у нас зависнут в немалых количествах недоработавшие мопы.
Моп родительского вызова тоже будет ждать, пока не отработает дочерний вызов. Глубина вызовов легко может достигнуть (десятков) тысяч единиц, в SandyBrige, к примеру, просто нет столько мопов.
Суть проблемы в том что, признав вызов обобщенной инструкцией мы тем самым признали программу обобщенным выражением. А дерево этого выражения благодаря рекурсии может быть любой высоты. С другой стороны, стек выражения у нас ограничен. А элементами стека являются индексы мопов, коих тоже ограниченное количество.
Но мы не привыкли так легко сдаваться, поэтому в дело вступает план Б.
План Б
Регистровые суперскалярные процессоры не имеют подобных проблем т.к. выявление связей между мопами происходит позднее — на этапе переименования регистров.
У нас же эти связи хранятся в стеке индексов мопов.
Может быть сохранить состояние стека? Сохранять индексы мопов мало, как мы выяснили, сами мопы тоже нуждаются в нашей заботе. Кажется естественным организовать сохранение мопов через стек, выделенный или нет, вопрос совершенно отдельный.
И тут мы сталкиваемся с теми же самыми проблемами, которые встречали при попытке сохранить регистры. А именно, при единой (для всех функций) идентификации мопов:
- порядок использования мопов зависит от предыстории вызовов
- внутри функции он определяется динамически
- нет никаких гарантий, что после операции FILL мы не получим конфликт с уже занятым мопом
Способ решения этих проблем предлагается тот же самый:
- кольцевой буфер мопов
- для каждой функции своя нумерация мопов, например, 0…
- FILL и SPILL делаются для целой функции, что позволяет при необходимости привязать стек регистров и стек мопов к одной области памяти
- FILL и SPILL делаются только для мопов, ожидающих завершения, следовательно, в стек укладывается еще и маска (или перечисление) сериализованных мопов
- стек индексов мопов мы тоже должны сохранить
На первый взгляд необходимость прогонять через память декодированные мопы представляется чудовищной. Но когда катехоламины догорают, становится понятно, что масштаб катастрофы не так уж и велик.
- хотя в современных процессорах параметры (по крайней мере их часть) передаются через регистры, при рекурсивном вызове сохранить параметры и негде, кроме как в стеке, кроме того:
- адрес возврата и frame pointer также сохраняются в стеке
- volatile регистры сохраняются в стеке вызывающей стороной
- non-volatile регистры тоже сохраняются в стеке, но уже вызываемой стороной
- выражения типа «a (m — 1, a (m, n — 1))» компилятор может развалить, вводя (явно или косвенно) временную переменную, равную a (m, n — 1). При этом уменьшается число мопов, которые надо сохранять.
- все несработавшие условные ветки к моменту безусловного перехода, коим является вызов функции, мы уже выкинули
- все мопы за грядущим вызовом мы также можем выкинуть или просто не загружать их, пользуясь техникой, аналогичной таковой в SandyBridge
- а можем оставить, тогда по возвращении из функции, бонусом получим готовый к исполнению или уже даже частично исполненный (независимый по данным) код
- в самом «экономном» варианте в стек попадет только один сериализованный моп вызова, а это уже мало отличается от передачи адреса frame-fuffer«а, например
- (де)сериализация мопов не выглядит затратной операцией, к тому же, она может производиться в фоновом режиме, заранее, не блокируя текущий возврат из функции
- сохранение мопов в стеке совместно с загрузкой по предположению является альтернативой кэшу l0m, который теперь попросту не нужен
- размер сериализованного мопа не слишком велик, для SandyBridge исходный размер мопа оценивается максимум в 147 бит, в сжатом виде — 85 бит (а там еще и x87, SSE и AVX всех мастей)
- сам факт, что снаружи становятся доступны технологические особенности процессора и могут быть скомпрометированы какие-либо технические секреты, автора не пугает. В конце концов, пусть процессор xor«ит эти данные с помощью одноразового блокнота.
Что дальше
До сих пор мы не обращали внимания на слабое место всех стековых машин — избыточные обращения к памяти.
Вот ими и займемся в следующей статье.
