Степени свободы в статистике

Статистический анализ играет важную роль в научных исследованиях, коммерческих деятельностях и в других областях. Однако, его результаты могут быть неточными, если не учитывать имеющиеся степени свободы. Степени свободы — это концепция, которая широко используется в статистике, и она позволяет более точно определить, насколько можно доверять полученным результатам.
В данной статье мы рассмотрим понятие степеней свободы, их роль в статистических расчетах, а также примеры их использования. Мы узнаем, как степени свободы помогают улучшить точность статистических выводов и в каких случаях их использование особенно важно.
Что такое степень свободы?
Степень свободы (Degree of Freedom, df) в статистике — это количество значений или наблюдений в выборке, которые могут быть изменены независимо друг от друга без изменения ее структуры. Можно сказать, что это количество переменных, которые оставляются свободными для варьирования после того, как структура выборки была определена.
Например, рассмотрим тест Стьюдента (t-Test), который используется для проверки гипотезы о равенстве средних значений двух выборок. В этом тесте степень свободы определяется как сумма степеней свободы двух выборок минус два (df = n1 + n2 — 2), где n1 и n2 — размеры выборок.
Чем больше степень свободы, тем меньше вероятность ложных выводов и тем более точными будут результаты теста. В случае же, если степень свободы будет низкой, то мы можем получить ложные результаты, так как мы не имеем достаточно информации для адекватной оценки статистических характеристик выборки.
Одним из важных факторов, влияющих на степень свободы, является размер выборки. Чем больше выборка, тем больше степень свободы, значит, чем больше выборка, тем менее вероятно получение ошибочных результатов в статистических тестах.
Также степень свободы важна при выборе статистической модели. К примеру, при построении линейной регрессии, степень свободы может использоваться для определения того, сколько переменных необходимо использовать в модели. Выбор модели слишком сложной или, наоборот, слишком простой (т.е. с недостаточной степенью свободы) может привести к неправильным выводам.
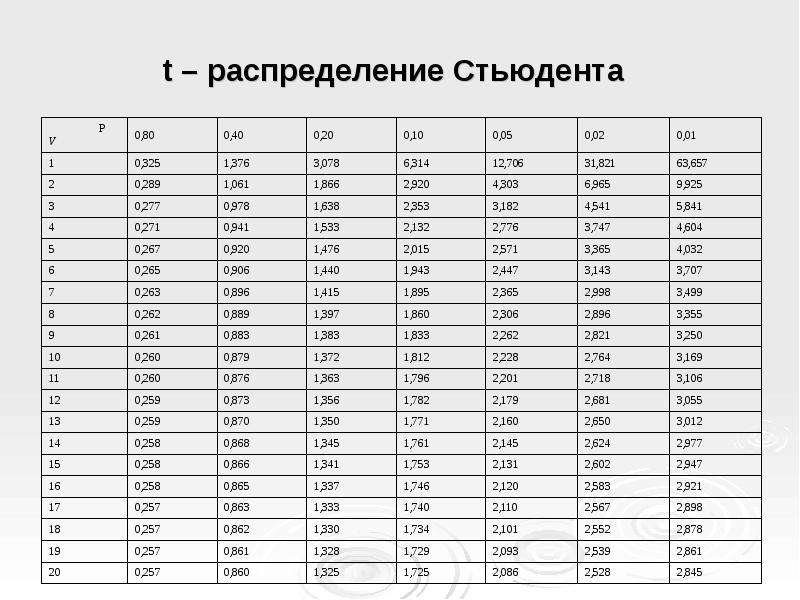
Таблица степеней свободы
Таблица степеней свободы — это таблица, которая заполняется в соответствии с типом и количеством переменных, которые используются в анализе статистических данных. Она используется для определения правильной формулы для расчета критических значений при проведении статистических тестов, таких как t-критерий, F-критерий и хи-квадрат тест.
В таблице степеней свободы могут быть два типа переменных: независимые (IV) и зависимые (DV). Количество степеней свободы для каждой переменной определяется путем вычитания единицы от общего количества наблюдений.
Для каждого теста, количество степеней свободы может быть разным в зависимости от характеристик выборки и типа теста. Например:
В t-критерии Стьюдента, количество степеней свободы зависит от размера выборки и количества групп, участвующих в сравнении. Если у нас есть две группы, количество степеней свободы будет равно n1+n2–2 (где n1 и n2 — это размер первой и второй групп соответственно).
В анализе дисперсии (ANOVA), количество степеней свободы будет зависеть от количества групп и количества элементов в каждой группе. Если есть количество групп (k) и общее количество элементов (N), то количество степеней свободы для межгрупповой дисперсии будет равно k-1, а для остаточной дисперсии будет равно N-k.
В хи-квадрат тесте, количество степеней свободы зависит от размера матрицы сопряженности. Если у нас есть матрица 2×2, то количество степеней свободы будет равно 1.
Таблица степеней свободы помогает убедиться, что мы используем правильные статистические формулы для расчетов, что позволяет получать более точные и надежные результаты при анализе статистических данных.
Примеры использования степеней свободы
Рассмотрим несколько практических примеров использования степеней свободы в статистике:
t-критерий Стьюдента. Это статистический тест, который используется для проверки значимости различия между средними двух независимых выборок. Для расчета t-критерия Стьюдента используется формула, которая включает в себя показатели меры центральной тенденции (среднее значение) и меры разброса (стандартное отклонение) для каждой выборки, а также степени свободы. В частности, степени свободы в расчете t-критерия Стьюдента определяются как сумма степеней свободы выборок, возведенная в степень двух, деленная на сумму квадратов степеней свободы выборок. Этот тест дает возможность оценить значимость различий между двумя выборками и узнать, велика ли вероятность случайного различия.

Предположим, что вы хотите определить, отличаются ли средние зарплаты мужчин и женщин в вашей компании. Вы можете использовать t-критерий для проверки этой гипотезы. Для этого вам нужно знать выборочные средние и стандартные отклонения для мужчин и женщин, а также общее число человек в каждой группе. После этого можно использовать формулу для расчета t-критерия, учитывая количество степеней свободы (количество людей в каждой группе минус 1).
Анализ дисперсии (ANOVA). Это статистический тест, который используется для сравнения средних значений нескольких групп. ANOVA расчитывается разнесением общего отклонения между группами на внутреннюю дисперсию (внутригрупповое отклонение) и межгрупповую дисперсию. Степени свободы в расчете ANOVA определяются как разность между общим числом наблюдений и числом использованных для расчета средних значений степеней свободы (то есть на 1 меньше числа групп). Внутригрупповые и межгрупповые степени свободы могут быть вычислены отдельно.

Предположим, что у вас есть несколько групп людей, проходящих тренировку для улучшения своего здоровья. Вы хотите определить, есть ли значимые различия в потере веса между этими группами. Для решения этого вопроса можно использовать ANOVA, для этого вам нужно знать выборочные средние и стандартные отклонения для каждой группы, а также общее количество участников в каждой группе. Затем используйте формулу для расчета F-критерия, учитывая количество степеней свободы, которое будет различаться в зависимости от количества групп и количества участников в каждой группе.
Хи-квадрат тест. Это статистический тест, в котором измеряется отклонение между фактическим и ожидаемым количеством наблюдений в наборе данных. Хи-квадрат тест может использоваться для проверки независимости двух переменных в категориальных данных, таких как таблицы сопряженности. Степени свободы в расчете Хи-квадрат теста определяются как разность между общим количеством наблюдений в таблице и количеством ограничений (то есть размерность таблицы минус 1, по каждому измерению). Если степени свободы достаточно высоки, то можно считать, что тест говорит о статистически значимых различиях между переменными.
Предположим, что у вас есть две переменных — пол (мужчина или женщина) и предпочитаемый вид спорта (баскетбол, футбол, хоккей и т.д.), и вы хотите проверить, есть ли статистически значимая связь между этими переменными. Для этого вы можете использовать хи-квадрат тест, для которого нужно разбить каждую категориальную переменную на несколько групп, затем измерить общее количество наблюдений в каждой ячейке таблицы. После того как вы подсчитаете значения статистики хи-квадрат, вы можете использовать таблицу степеней свободы, чтобы определить, является ли полученный результат значимым для определенного уровня доверия.
В корреляционном анализе, степени свободы используются для вычисления коэффициента корреляции между двумя переменными и определения статистической значимости этой связи. Обычно, чем больше степеней свободы, тем точнее оценки корреляции. Количество степеней свободы определяется как общее число наблюдений минус число неизвестных параметров.
Например, если мы исследуем связь между уровнем образования и доходом, то количество степеней свободы будет равно количеству наблюдений минус два, так как два параметра (уровень образования и доход) неизвестны.
Преимущества и недостатки
Преимущества использования степеней свободы в статистике включают следующее:
Корректность статистических тестов: использование степеней свободы позволяет правильно оценивать дисперсию и скорректировать стандартные ошибки. Это обеспечивает более точные тесты на статистическую значимость.
Увеличение мощности тестов: использование правильных степеней свободы может увеличить мощность статистических тестов. Это позволяет увидеть статистически значимые различия там, где их может не быть при использовании неправильных степеней свободы.
Более надежные выводы: правильное использование степеней свободы позволяет избежать ошибок первого и второго рода. Это позволяет давать более точные и надежные научные выводы.
Однако, использование степеней свободы также имеет некоторые ограничения:
Количество данных: необходимо иметь достаточно большое количество данных, чтобы определить степени свободы. В противном случае могут возникнуть ошибки в статистических тестах.
Некоторые статистические тесты зависят от предположений: некоторые статистические тесты, такие как t-тесты, предполагают нормальность распределения данных. Если данные не соответствуют этим предположениям, использование степеней свободы может привести к ошибкам.
Ошибки вязкости: иногда степени свободы могут быть неверными из-за ошибок в вычислениях. Это может привести к неправильным выводам из статистических тестов.
Заключение
Таким образом, степени свободы являются одним из ключевых параметров в статистических расчетах и оказывают большое влияние на результаты анализа данных. При этом, важно понимать, что оптимальное количество степеней свободы зависит от многих факторов, включая размер выборки и число независимых переменных. Поэтому, для правильного выбора количества степеней свободы, необходим обширный опыт в анализе данных и статистике.
Также следует отметить, что степени свободы являются только одним из аспектов статистического анализа, и их применение требует определенных знаний в области статистики.
Полезные рекомендации
Напоследок хочу порекомендовать несколько полезных бесплатных вебинаров от OTUS. Регистрация доступна по ссылкам ниже:
Построение архитектуры с иcпользованием облачных сервисов AWS
Профессия Системный Аналитик. Путь с нуля до Middle
Бережливое управление требованиями
