Статистика на примерах с Python #1
Содержание:
1.1 Общая информация
1.2 Генеральная совокупность и выборка
1.3 Типы переменных. Количественные и номинативные переменные
1.4 Меры центральной тенденции

1.1 Общая информация
Будем работать в Jupyter notebook. используем библиотеки numpy, pandas, matplotlib, scipy
Импортируем библиотеки
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy
%matplotlib inlineИспользуем данные из kaggle, базу данных Титаника:
https://www.kaggle.com/competitions/titanic

train = pd.read_csv('/kaggle/input/titanic/train.csv')
age = train['Age']
train.head()
1.2 Генеральная совокупность и выборка
В нашем случае это для нас генеральная совокупность, то есть тут абсолютно все данные. Однако в действительности же не всегда удается получить всю генеральную совокупность. Примеру рост всех людей на планете Земля узнать практически невозможно, а вот рост людей, побывавших на Луне, очень даже просто узнать, так как их мало.

У нас пример с возрастом. На Титанике было не так много людей, поэтому надеюсь у нас есть данные всех пассажиров. Поэтому будем считать, что у нас имеется генеральная совокупность.

А вот это уже считается выборкой, так как мы сделали срез данных от 15-го индекса до 25-го:

1.3 Типы переменных. Количественные и номинативные переменные
1) Номинативная (качественная) переменная. Переменная, каждое значение которой указывает на принадлежность объекта к группе (категории). Номинативная переменная разделяет все объекты на непересекающиеся по определенному признаку (пол, класс и т. д.)
2) Ранговые переменные — это переменные, которые могут быть упорядочены, но не имеют фиксированного интервала между значениями. Другими словами, вы можете сказать, что один объект выше или ниже другого, но вы не можете сказать, насколько он выше или ниже.
3) Метрические (количественные переменные) — это переменные, которые имеют количественное значение, которое можно измерить. Они могут быть дискретными или непрерывными. Они могут принимать любые значения на некотором промежутке, например, рост человека может принимать значения от 160 до 190 см. Количественные переменные делятся на два подтипа:
Непрерывные переменные могут принимать любые значения на некотором промежутке, например, рост человека, вес человека, температура воздуха (рост человека; вес человека; температура воздуха).
Дискретные переменные могут принимать только определенные значения, например, количество детей в семье, количество комнат в квартире, количество баллов, набранных на экзамене (количество детей в семье; количество баллов, набранных на экзамене; количество единиц товара, проданных за день).

Рассмотрим типы данных
1) Номинативной переменной будет пол человека
Sex = train['Sex']
fig, ax = plt.subplots()
plt.hist(Sex, bins=50)
ax.set_ylabel("")
ax.set_xlabel("")
print(Sex.value_counts())
2) Ранговые переменные
У нас это Pclass (номер класса)
Pclass = train['Pclass']
fig, ax = plt.subplots()
plt.hist(Pclass)
ax.set_ylabel("")
ax.set_xlabel("")
print(Pclass.value_counts())
подскажите, как сделать красивее
3) Метрические (количественные переменные):
fig, ax = plt.subplots()
plt.hist(age, bins=50)
ax.set_ylabel("")
ax.set_xlabel("")
Нормально)
SibSp = train['SibSp']
fig, ax = plt.subplots()
plt.hist(SibSp)
ax.set_ylabel("")
ax.set_xlabel("")
print(SibSp.value_counts())
1.4 Меры центральной тенденции
1) Мода (Mode) — это наиболее часто встречающееся значение в наборе данных. Мод может быть несколько.

Если в наборе данных несколько мод, то говорят, что распределение данных является бимодальным или мультимодальным. Это означает, что в данных существует два или более значения, которые встречаются одинаково часто или почти одинаково часто.

2) Медиана — это значение, которое находится в середине набора данных, упорядоченного по возрастанию. При нечетном количестве данных медиана является одним из значений набора. Например, если у нас есть набор данных {1, 2, 3, 4, 5}, то медиана равна 3.
При четном количестве данных медиана является средним арифметическим двух значений, расположенных в середине набора. Например, если у нас есть набор данных {1, 2, 3, 4, 5, 6}, то медиана равна (3 + 4) / 2 = 3,5.

четко и понятно
3) Среднее значение — это мера центральной тенденции, которая рассчитывается как сумма всех значений в наборе данных, деленная на количество значений.

Существует среднее значение для генеральной совокупности и среднее значение для выборки. Они по разному обозначаются. Мы будем использовать большую латинскую букву М для обозначения среднего в генеральной совокупности:


Есть и такие обозначения:

мама я художник
Может показаться, что все эти меры центральной тенденции не имеют смысла, ведь можно использовать лишь одну — среднее значение. Однако это не всегда это правильно, как может показаться. На следующем примере показано, что эти меры отличаются

Если вам интересно, что будет, если использовать только среднее значение, то вот лекция на Ted на эту тему:
https://www.ted.com/talks/hans_rosling_the_best_stats_you_ve_ever_seen

Рассмотрим на Python меры центральной тенденции
1) Мода (Mode)
Рассмотрим на примере возраста. Для начала превратим наш список в массив numpy, а потом удалим все nan. Там было 177 пустых значений (nan). Если бы мы попытались определить моду с таким количеством nan, то модой было бы именно это пустое значение (nan).
age_without_nan = age.to_numpy()
age_without_nan = age1[~np.isnan(age_without_nan)]А следующим кодом находим моду:
mode = scipy.stats.mode(age_without_nan)
print('Мода =', mode)
2) Медиана
Рассмотрим теперь медиану. Пример на том же возрасте (age)
median = scipy.ndimage.median(age_without_nan)
print('Медиана =', median)
3) Среднее значение
mean = scipy.mean(age_without_nan)
print('Среднее значение =', mean)
Свойства среднего

Первая формула говорит нам о том, что если мы к каждому значению в нашей генеральной совокупности прибавим (отнимем) некое число, то среднее значение изменится ровно на это число в положительную (в отрицательную) сторону. Это очень легко объяснить наглядно на рисунке справа. Это тоже самое, если представить, что в улье ровно посередине живет королева, и если мы каждую пчелку сдвинем на 10 см, то и королева сдвинется на 10 см, так как она находится всегда посередине.
a = [1, 2, 3, 4, 5, 6, 7, 8, 9 ,10]
average_a = sum(a) / len(a)
print('Среднее значение =', average_a)
new_list = [x+10 for x in a]
average_new_list = sum(new_list) / len(new_list)
print('Среднее значение, при X(i)+10 =', average_new_list)
print('Разница =', average_new_list - average_a)
Вторая формула говорит нам о том же самом, только при умножении, то есть если каждое значение умножить на некое число, то и среднее будет больше в такое же количество раз. Тут пример с пчелами тоже подойдет))
a = [1, 2, 3, 4, 5, 6, 7, 8, 9 ,10]
average_a = sum(a) / len(a)
print('Среднее значение =', average_a)
new_list = [x*10 for x in a]
average_new_list = sum(new_list) / len(new_list)
print('Среднее значение, при X(i)*10 =', average_new_list)
print('Разница в', average_new_list / average_a, 'раз')
Третья формула говорит нам о том, что если мы отнимем от каждого значения среднее значение и все эти ответы просуммируем, то у нас получится ноль.
Сейчас мы отнимем от каждого значения среднее и просуммируем результаты:
(1 — 5,5) + (2 — 5,5) + (3 — 5,5) + (4 — 5,5) + (5 — 5,5) + (6 — 5,5) + (7 — 5,5) + (8 — 5,5) + (9 — 5,5) + (10 — 5,5) = 0
sum_ = 0
for i in a:
w = i - average
sum_ = w + sum_
print('sum( X(i) - average ) =', sum_)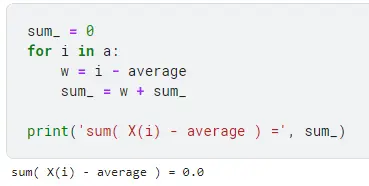
Всего наилучшего!

