Создание фотомозаик с помощью языка Wolfram Language (Mathematica)
Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, можно здесь (архив, ~3 МБ).Введение
До Нового 2015-го года осталось уже менее суток: In[1]:=
Out[1]=
Мне хотелось бы поздравить всех с Наступающим Новым 2015-м годом и рассказать о том, как вы можете сделать своим близким необычный подарок в виде фотомозаики, созданной с помощью системы Mathematica 10 и языка Wolfram Language.
Идея фотомозаики в целом довольно проста: создать изображение на основе коллекции других изображений небольшого размера.
Для того, чтобы создать фотомозаику можно действовать двумя основными способами:
Простой способ: разбить изображение на фрагменты фиксированного размера, после чего подобрать каждому фрагменту наиболее «похожее» на него изображение из заданной коллекции и заменить этот фрагмент на него. В результате, чем меньше размер фрагмента и больше коллекция, тем качественнее будет фотомозаика. Сложный способ: по сути повторяет первый способ за исключением того, что разбиение исходного изображения производится некоторым «адаптивным» алгоритмом на фрагменты различного размера. Для упрощения рассматриваемой задачи будем создавать мозаику из квадратных миниатюр.Создание коллекции изображений Безусловно, можно использовать любую коллекцию изображений, которая у вас есть, будь то семейные фото или фотографии из путешествия.Я не думаю, что мои коллекции такого рода будут очень интересны большинству читателей, поэтому в качестве коллекции я буду использовать набор изображений какого-нибудь известного человека. В качестве такого человека я возьму того, кто известен абсолютно всем, а именно — Арнольда Шварценеггера.
Для создания коллекции изображений воспользуемся парсером с сайта Zimbio:
In[2]:=
In[3]:=
Импортируем все имеющиеся фото из профиля Арнольда:
In[4]:=
Всего было импортировано 5436 фото:
In[5]:=
Out[5]=
Общий «вес» которых равен почти 5 ГБ.
In[6]:=
Out[6]=
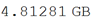
Можем посмотреть на коллекцию мельком, составив коллаж из 150 случайно выбранных изображений:
In[7]:=
Out[7]=
Простая фотомозаика Приступим к созданию простой фотомозаики.Для начала укажем директорию, в которой хранится коллекция наших изображений:
In[8]:=
Теперь подгрузим пути к каждому из изображений:
In[9]:=
Out[9]//Short=
Сохраним число изображений в отдельной переменной:
In[10]:=
Out[10]=
Теперь создадим коллекцию миниатюр изображений, так как, очевидно, нам не потребуются изображения в их исходном размере. Размер каждой из миниатюр не бедет превышать 150×150 пикселей (по умолчанию).
In[11]:=
In[13]:=
In[14]:=
Подгрузим пути к каждой из миниатюр:
In[15]:=
Теперь загрузим все миниатюры в систему:
In[16]:=
Вычислим для каждой из миниатюр ее средний RGB цвет:
In[17]:=
Создадим функцию, которая будет для некоторого изображения подбирать наиболее близкую к нему миниатюру. При этом предусмотрим возможность случайного выбора из n ближайших миниатюр (это потребуется для того, чтобы в фотомозаике отсутствовали области, заполненные одной миниатюрой, что встретится, скажем, если большой участок изображения имеет один цвет).
In[18]:=
Out[18]=
Создадим функцию, составляющую фотомозаику:
In[20]:=
Зададим изображение, мозаику которого мы хотим получить:
In[21]:=
Посмотрим, как будет выглядеть мозаика в случае, если берется ближайшая миниатюра при последовательном уменьшении миниатюр:
In[22]:=
Out[22]=
На последней фотомозаике наиболее отчетливо заметен тот эффект, о котором говорилось ранее — области, заполненные одной миниатюрой на участках изображения с одним (или очень близкими) цветом.
Для того, чтобы избавиться от этого, установим случайный выбор из 10 ближайших миниатюр:
In[23]:=
Out[23]=
Безусловно, с помощью этого алгоритма можно создавать любые мозаики такого рода:
In[24]:=
Out[24]=
Адаптивная фотомозаика Создадим функцию, которая будет разбивать изображение на меньшие изображения адаптивным способом.Функция adaptiveImagePartition работает следующим образом:
она представляет собой итеративное адаптивное разбиение с помощью шагов, приведенных ниже;
функция toParts вызывает функцию parts применительно к каждому изображению (или исходному изображению на первом шаге);
функция parts дробит изображение на 4 равные части (прямыми, проведенными через середины противолежащих сторон изображения) и отдает результат функции toParts;
для каждого из четырех полученных фрагментов вычисляется его средний цвет, после чего ищутся попарные расстояния между средними цветами с помощью функции ColorDistance (согласно стандарту CIE2000), затем ищется среднее значение расстояния. Если оно больше значения prec, то исходное изображение заменяется на четыре новых, в противном случае изображение оставляется в прежнем виде;
к полученному набору изображений применяется правило обработки rule.
In[25]:=
In[26]:=
In[27]:=
Зададим базовое изображение:
In[28]:=
Посмотрим на шаги работы созданной функции:
In[29]:=
Out[29]=
Изменив обработчик, мы можем получить адаптивную пикселизацию:
In[30]:=
Out[30]=
Наконец, если в качестве обработчика указать замену фрагмента изображения на ближайшую миниатюру, то получим:
In[31]:=
Out[31]=
Заключение Надеюсь, что мой пост смог вас порадовать и заинтересовать. Безусловно, можно создать еще более сложные алгоритмы для фотомозаик, учитывающие: не только средний цвет, но и доминантные цвета фрагментов и миниатюр (DominantColors); морфологию изображений; более сложное адаптивное разбиение и пр. Но, думаю, созданных алгоритмов может быть уже вполне достаточно для того, чтобы сделать оригинальный подарок вашим близким к Наступающему Новому 2015-му году.Ресурсы для изучения Wolfram Language (Mathematica) на русском языке: http://habrahabr.ru/post/244451
