Совсем просто про минимальное идеальное хеширование основанное на графах
Представим, что перед нами стоит классическая задача получить данные по какому-то ключу. Причем количество данных и их ключей заранее известно.Как решать подобную задачу?
Если количество пар ключ-значение заведомо невелико, то бывает смысл просто захардкодить. Но если таких значений много миллионов?
Можно просто перебором пройтись по списку пока не встретиться нужное значение ключа. Но тогда сложность будет линейная O (N), что в данном случае должно расстроить любого инженера. А какая сложность алгоритма тогда требуется? Которая не зависит от количества данных и выполняется за фиксированное время, т. е. константная сложность O (1).
Как можно получать данные за фиксированное время?
ХешированиеЕсли расположить данные в памяти последовательно, то зная смещение, где находится нужная информация, можно получать доступ, который не будет зависеть от изначального количества данных.Другими словами нам надо найти способ преобразовывать ключ в смещение, где будут находиться данные. Смещение — это просто целое число: [0, n — 1] где n — количество сохраняемых значений.
На помощь приходят хеш-функции, задача которых как раз заключается в преобразовании ключей в целые числа. Такие числа могут быть интерпретированы как смещения, по которым сохраняют данные.
Но, к сожалению, хеш-функции порождают коллизии, то есть два разных ключа могут давать одинаковое смещение.
Исходя из задачи, у нас фиксированное и заранее известное количество данных, что дает возможность избежать подобных проблем.
Идеальное хеширование Идеальная хеш-функция (Perfect Hash Function) — это такая хеш-функция, которая преобразует заранее известное статическое множество ключей в диапазон целых чисел [0, m-1] без коллизий, т. е. один ключ соответствует только одному уникальному значению. А если количество результирующих значений такое же как и количество входящих ключей, такая функция называется Минимальной Идеальной Хеш-функцией (Minimal Perfect Hash Function).Рассмотрим пример минимальной идеальной хеш-функции основанной на случайных графах.
Давайте пофантазируем и представим, что каждый ключ соответствует одному уникальному ребру, и, соответственно, двух вершин.Тогда ключ может быть представлен в виде такого примитивного графа:
 Рис 1. Пустой граф, где ребро соответсвует ключу и описывается через две вершины.
Рис 1. Пустой граф, где ребро соответсвует ключу и описывается через две вершины.
Так как ключ представлен в виде ребра, а ребро всегда соединяет как минимум две вершины, значит искомая функция может выглядеть примерно так:
h (key) = g (node1, node2)
где h (key) — это минимальная идеальная хеш-функция, значение которой описывает ребро, key — ключ, g — некая пока неизвестная функция зависящая от вершин графа node1 и node2. Так как они должны зависеть от ключа, то получается
h (key) = g (f1(key), f2(key))
По сути для f1 и f2 можно выбрать любые хеш-функции, которые будут применяться для одного ключа.
Осталось определить неизвестную функцию g (), которая описывает взаимосвязь двух узлов f1(key), f2(key) и ребро.
Вот здесь начинаются фокусы Для простоты определим значение ребра как сумма значений узлов, соединяющиеся этим ребром.Так как ребро соответствует только одному ключу, то это и есть искомое значение, результат минимальной идеальной функции.h (key) = (g1(f1(key)) + g2(f2(key))) mod m
где h (key) — это значение ребра, f1(key) — это первый узел графа, g1 — значение этого узла, f2(key) — второй узел, g2 — значение второго узла, m — количество ребер.
Если еще проще, то
значение минимальной идеальной функции = (значение узла 1 + значения узла 2) mod количество ребер.
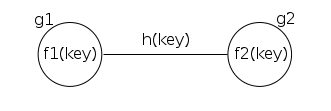 Рис 2. Представление одного ключа в графе.
Рис 2. Представление одного ключа в графе.
Другими словами, чтобы определить номер узлов используется хеш-функции, и часто бывают коллизии, поэтому один узел может содержать множество ребер.
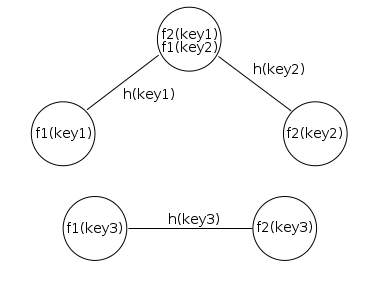 Рис 3. Коллизии в хеш-функциях порождают несколько ребер на одной вершине. Так же вершины одного ключа могут не соеденяться с вершинами другого ключа.
Рис 3. Коллизии в хеш-функциях порождают несколько ребер на одной вершине. Так же вершины одного ключа могут не соеденяться с вершинами другого ключа.
Вот где соль Определившись как взаимосвязаны узлы графа с их ребрами, мы сперва определяем значения ребер h (key) (это просто инкрементный индекс), которые будут заведомо уникальны, а потом подбираем значения узлов.Например значение следующего узла можно посчитать так:
g2(f2(key)) = h (key) — g1(f1(key))
или
значение узла 2 = значение ребра — значения узла 1
Осталось только пройтись по графу, взять 0 за начальное значение первого узла подграфа и посчитать все остальные.
К сожалению данный подход не работает если граф получился зацикленным. Так как нет способа заранее гарантировать незацикленность графа, то в случае обнаружения зацикленности придется перерисовать граф с другими хеш-функциями.
Зациклинность лучше всего проверять удалением вершин с только одним ребром. Если вершины останутся, то граф зациклен.
На простом примере Теперь пришел черед описать сам алгоритм на примере.Задача: Имеется множество ключей состоящих из названий 12 месяцев. Необходимо создать минимальную идеальную хеш-функцию где каждый месяц транслируется в только одно уникальное целое число в диапазоне [0, 11].
1. Проходим по всем ключам и добавляем вершины и ребра. Для этого выбираем две хеш-функии f1 и f2.
Например: Для ключа jan получаем номер первого узла f1(jan) := 4 и номер второго узла f2(jan) := 13Для ключа feb, f1(feb) := 0, f2(feb) := 17и так далее.
2. Проверяем получился ли граф зацикленным, если да, то повторяем шаг №1 заново и при этом меняем хеш функции f1/f2.Вероятность появления цикла в графе зависит от количества возможных вершин. Поэтому введем понятие как фактор размера графа. Количество узлов определяется как:
m = c * n
где m — количество узлов в графе, с — константный фактор размера, n — количество ключей.
В случае когда ребро соединяет 2 вершины вероятность появления цикла в графе считается по формуле:
p = sqrt (1 — (2/c)**2)
И при c=2.09, вероятность получается примерно равняется 0.29.
3. В случае успешного создания незацикленного графа, надо пройтись по всем узлам и посчитать их значение по формуле
g2(f2(key)) = h (key) — g1(f1(key))
или
значение дочернего узла = индекс ребра — значение узла предка
В результате имеем такой граф.
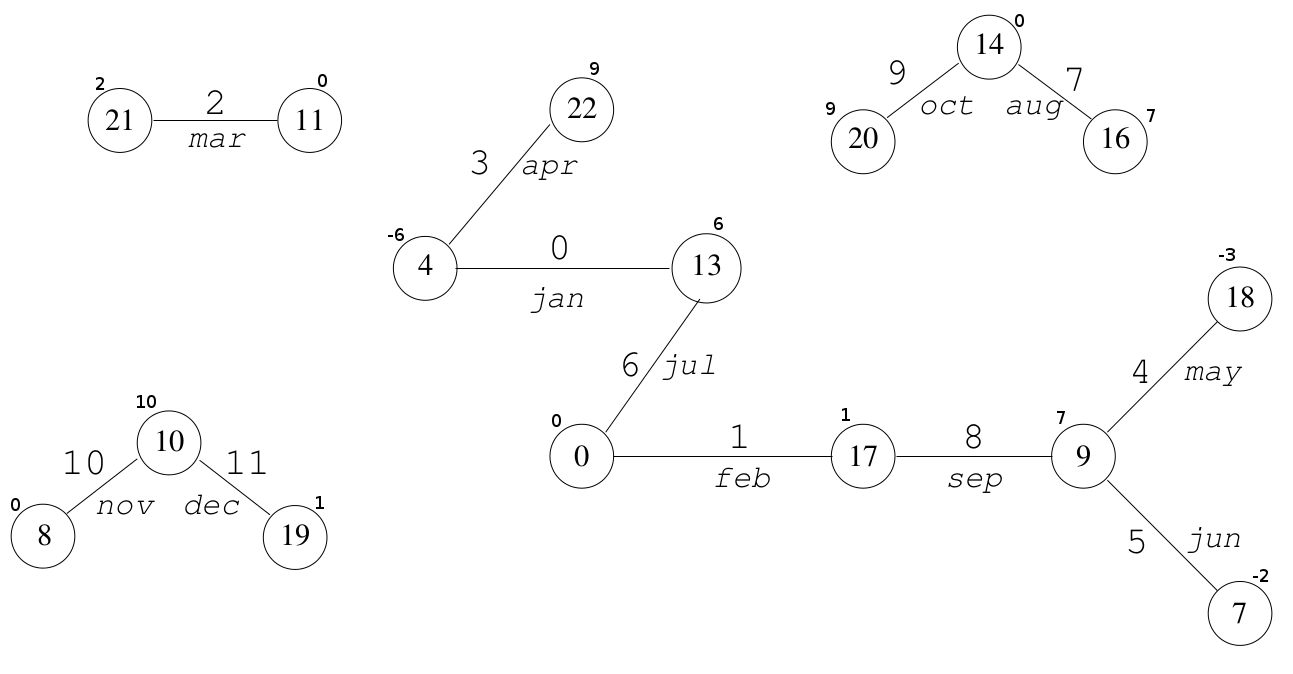 Рис 4. Результирующий граф, где ключами выступают имена месяцев и использованы случайные хеш-функции для получения номеров вершин. Числа возле узлов есть значение узла.
Рис 4. Результирующий граф, где ключами выступают имена месяцев и использованы случайные хеш-функции для получения номеров вершин. Числа возле узлов есть значение узла.
Например, присваиваем узлу с номером 0 значение 0 и идем по его ребру с индексом 6:
g2(13) = 6 — 0 = 6, узел с номером 13 получает значение 6 и т. д.
Лукап Допустим нам надо получить уникальный индекс по ключу sep.Используем те же хеш-функции, которые были использованы для создания графа: f1(sep) := 17f2(sep) := 9
Получив номера вершин, складываем их значение:
h (sep) = (g (17) + g (9)) mod 12 = (1 + 7) mod 12 = 8
Данный алгоритм называется CHM и реализован в библиотеке CMPH.
Почитать 1. Z.J. Czech, G. Havas, and B.S. Majewski. An optimal algorithm for generating minimal perfect hash functions., Information Processing Letters, 43(5):257–264, 1992.2. CHM.3. mphf — моя реализация CHM на C++.
