Совместное редактирование. Часть 2

Добрый день! Недавно мы начали цикл статей о совместном редактировании. В первой статье я рассказал о задаче неблокирующего редактирования и возможных подходах к его реализации. Напомню, что в итоге в качестве алгоритма мы выбрали Operation Transformation (OT). Также был анонсирован рассказ о его клиент-серверном варианте, и сегодня я освещу подробности его работы. Кроме того, вы узнаете, почему отмена в OT работает иначе и чем грозит столкновение с суровой реальностью.
Дальше вас ждет много алгоритмов и диаграмм. Думаю, вам будет интересно.
В конце предыдущей статьи я отметил, что трудности в реализации подхода ОТ можно обойти за счет центрального сервера. В отличие от алгоритма с равноправными клиентами, использование сервера позволяет ввести общий для всех порядок операций — порядок операций на сервере. Соответственно, в любой момент времени состояние документа на сервере характеризуется одним числом — ревизией.

При этом состояние документа у любого из клиентов в любой момент времени можно представить как некоторую ревизию на сервере и определенное количество пока еще несогласованных с сервером локальных операций.
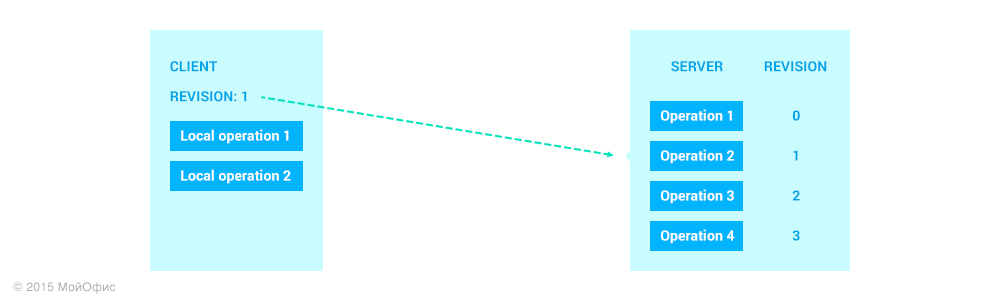
От сервера к клиенту
Для начала разберем, что происходит, когда клиенту от сервера приходит новая операция. В этой ситуации все достаточно однозначно. Предполагается, что все операции к нам приходят в том порядке, в котором они применяются на сервере. По этой причине ревизия операции нам известна (ревизия на клиенте + 1).
Ревизия 1 — это наиболее позднее общее состояние документа для сервера и этого клиента. Вспомним о трансформациях, которые мы рассмотрели в предыдущей статье. С их помощью мы можем «свести» разные пути модификаций документа:
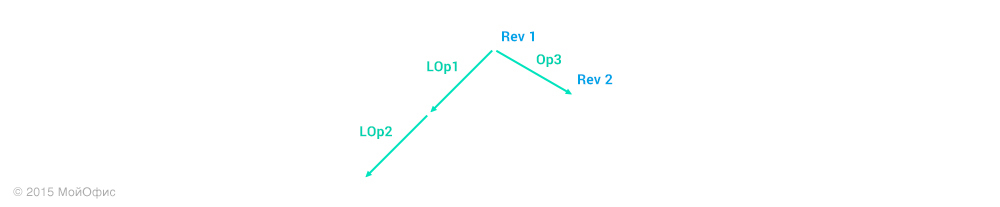
Для наглядности в этой и последующих схемах я буду использовать сокращения, где Operation3 — Op3, Local operation 1 — LOp1 и так далее. Правое «плечо» — это действия, которые выполняются на сервере. А левое — на клиенте. Воспользуемся свойством трансформаций, которое описано диаграммой в прошлой статье:
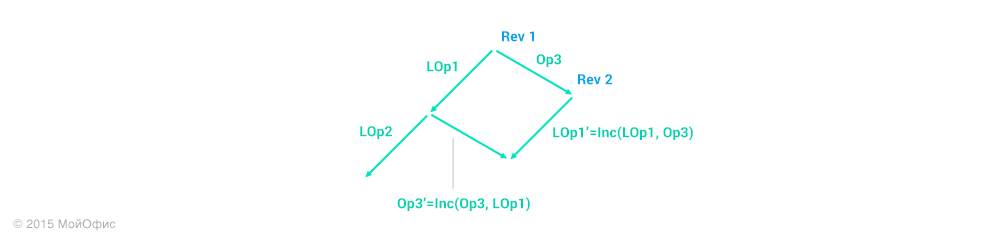
Повторим это действие еще раз:
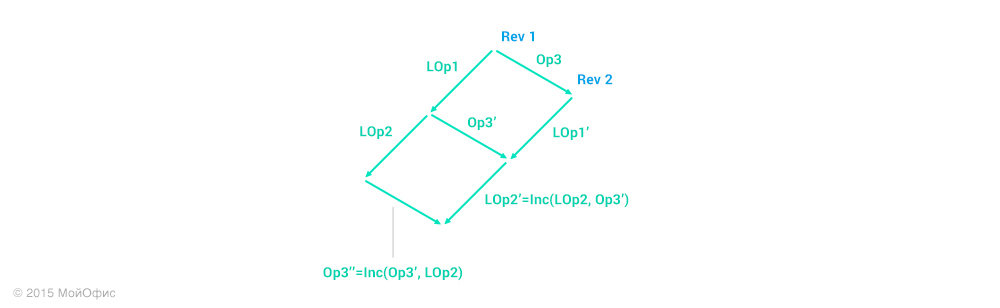
Дальше мы можем действовать в двух направлениях:
- Применить на клиенте операцию Op3'', инкрементировать ревизию и заменить локальные операции (LOp1, LOp2) на (LOp1', LOp2'').
- Откатить локальные операции и последовательно применить Op3, LOp1', LOp2''.
Какой бы вариант мы ни выбрали, в результате получим вот такое состояние клиента:
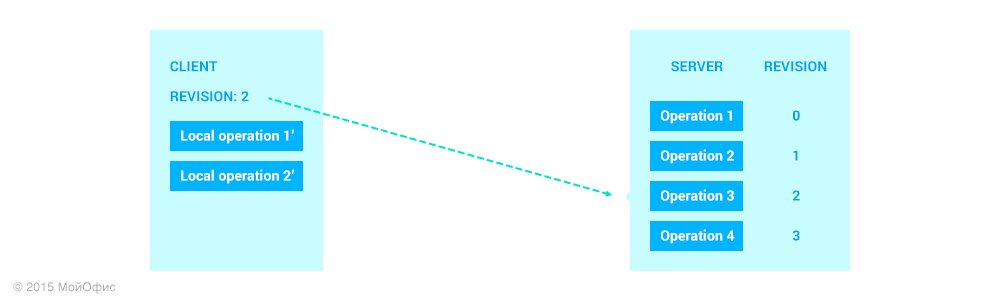
Исходя из всех приведенных на текущий момент соображений, все выглядит так, что результаты в обоих вариантах будут аналогичными. И первый из них предпочтительнее по соображениям производительности. Но мы используем именно второй способ. Я расскажу, чем это обусловлено, в одной из следующих статей. А пока примем это как есть и продолжим.
От клиента к серверу
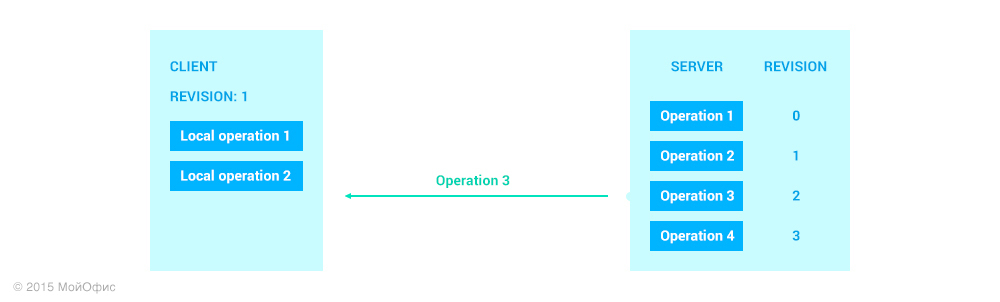
После того как мы разобрали отправку данных от сервера в сторону клиента, рассмотрим операции в обратном направлении. Вернемся к тому же состоянию, что и в примере выше:
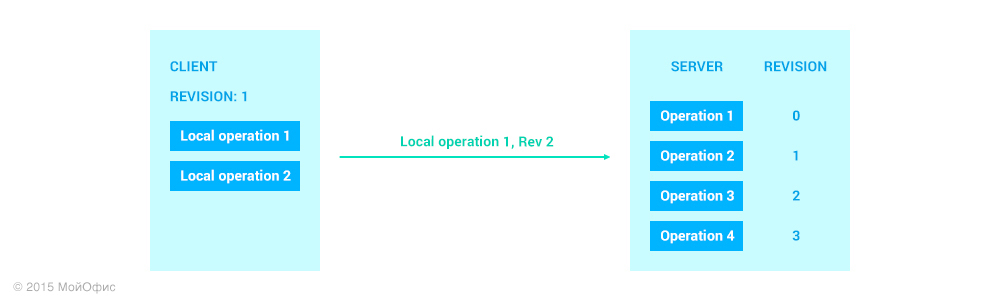
Как вы можете заметить, вместе с самой операцией клиент отсылает ревизию, которая является общей для клиента и сервера на текущий момент. Это избавляет сервер от необходимости с помощью истории восстанавливать ревизию, на которой была основана присланная операция. Вновь применим трансформации:
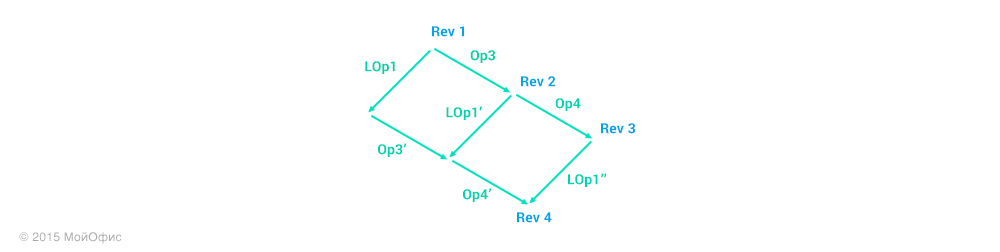
Здесь мы можем видеть, что на сервере необходимо применить именно операцию LOp1′′ и, соответственно, увеличить ревизию. Кроме того, трансформированную операцию мы должны разослать остальным клиентам, которые работают с документом:
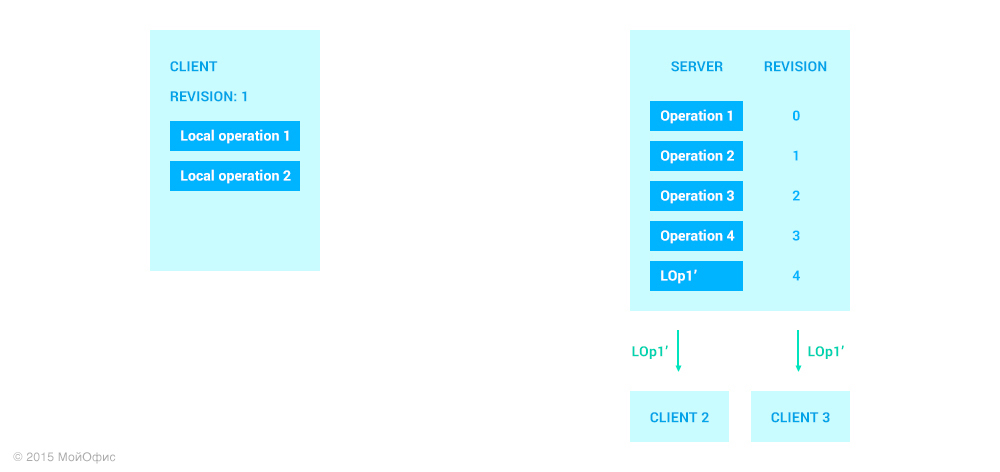
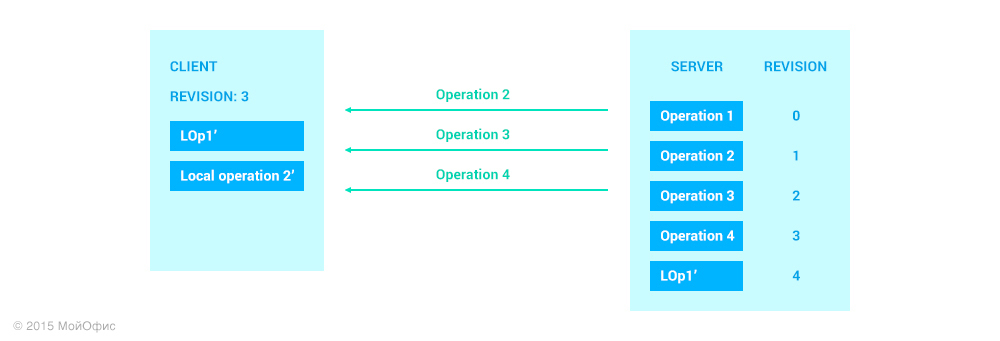
Обратите внимание на то, что состояние клиента не изменилось. Для того чтобы он смог увеличить ревизию, серверу необходимо отправить ему подтверждение. При этом подразумевается, что канал связи сохраняет порядок доставки сообщений, а это значит, что предварительно клиенту будут пересланы все операции с ревизией меньшей, чем у LOp1′.
При этом порядок действий, когда клиент получает операции от сервера, гарантирует, что после всех трансформаций первая из локальных операций будет иметь значение LOp1′, такое же, как соответствующая операция на сервере.
Получив сообщение с подтверждением, клиент увеличивает значение ревизии. Значение этой ревизии будет равно ревизии на сервере, которая соответствует отправленной операции. Также мы удаляем LOp1′ из списка локальных операций клиента, так как теперь она есть и на сервере.
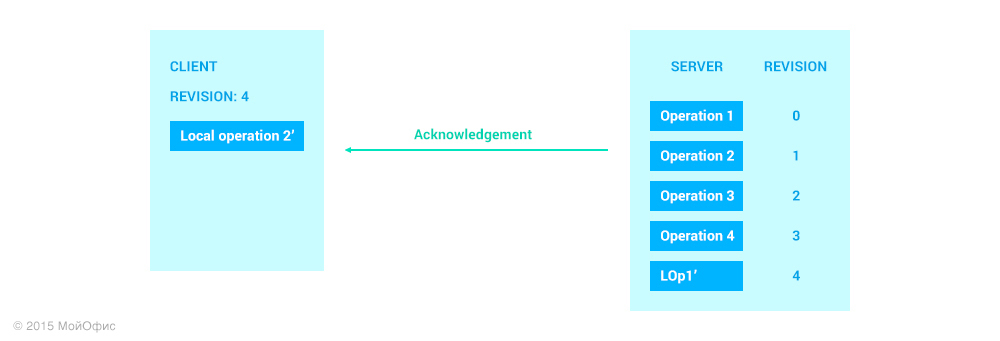
А что произойдет дальше с Local Operation 2?
«Что происходит дальше с Local Operation 2?» — спросите вы. Все описанное выше работает для первой локальной операции. Посмотрим, что будет со второй. Представим, что как только клиент добавил Local Operation 2, мы сразу отсылаем ее на сервер. При этом вполне возможно, что на сервере между этими операциями могут «вклиниться» операции от других клиентов:
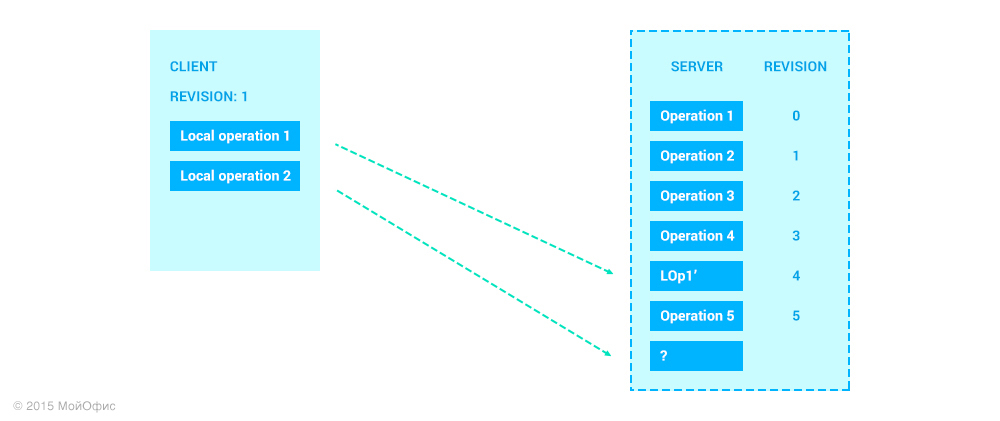
Теперь, чтобы понять, какую операцию применить на сервере, необходимо разрешить следующую задачу:
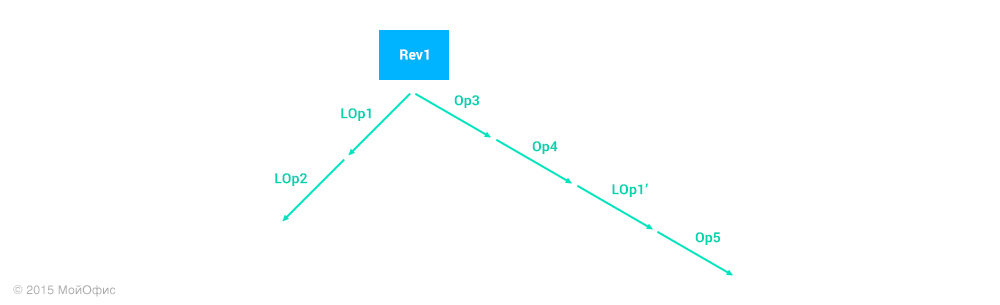
С точки зрения теории нам ничего не мешает это сделать. Достаточно много раз применить уже упомянутые трансформации, чтобы получить нужную операцию:
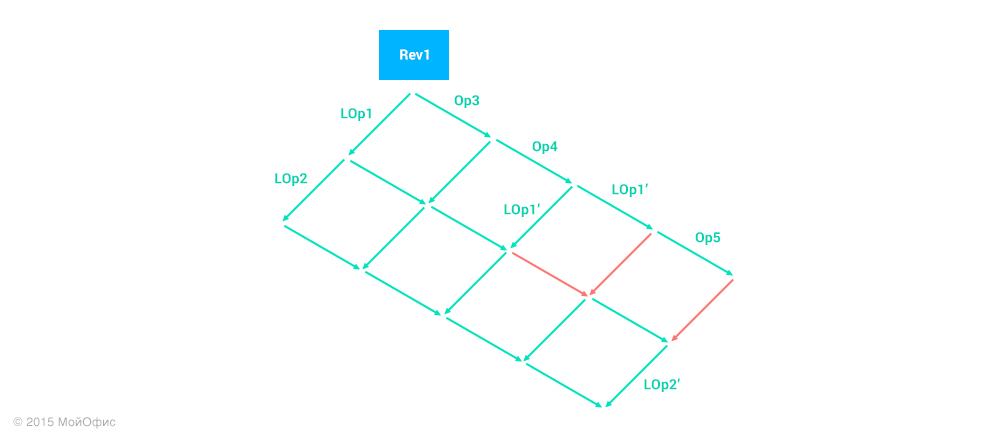
Я не стал обозначать все преобразования, иначе схема получилась бы очень громоздкой. Но стоит отметить, что операции, соответствующие красным стрелкам, — пустые (тождественные). Это означает, что операция LOp2′ — это те изменения, которые нам следует применить на сервере.
Давайте рассмотрим эти вычисления с практической точки зрения. Чтобы выполнить данные трансформации, серверу необходимо:
- Знать ревизию, с которой начинается диаграмма. В этом нет сложности, так как вместе с операцией мы можем отправить базовую ревизию.
- Иметь информацию о предыдущих локальных операциях данного клиента. В приведенной схеме это LOp1, но в общем случае их может быть любое количество. Причем важно иметь состояние этих операций именно на момент отправки LOp2, поскольку выше было показано, что, когда операция приходит от сервера, локальные операции будут трансформированы, что может привести к их изменению.
Условие «Иметь информацию о предыдущих локальных операциях клиента» означает, что нам необходимо либо отсылать вместе с LOp2 все предыдущие локальные операции, либо восстанавливать их с помощью трансформаций на сервере. Просто использовать операции от этого клиента в истории на сервере нельзя, так как они уже подверглись трансформациям. В первом случае сильно увеличивается сетевой трафик, а во втором возрастает нагрузка на сервер.
В алгоритме, который используют Google Docs и Wave, применяется простое, но эффективное решение, которое позволяет не выбирать из двух зол. Идея заключается в том, чтобы не отправлять следующую локальную операцию до тех пор, пока не получено подтверждение о том, что предыдущая была успешно применена на сервере. В нашем случае это означает, что LOp2 будет отправлена только после того, как мы получили от сервера сообщение с подтверждением (acknowledgement), относящимся к LOp1:
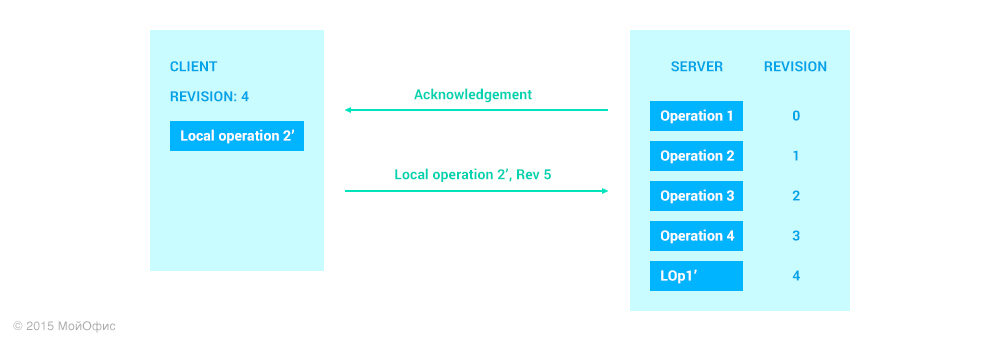
Этот же подход используется и нами.
Итог
Как эти правила работают «вживую», можно посмотреть на слайдах.
Client-Server OT в действии
Возможность совместного редактирования делает такую обыденную функцию, как отмена действия пользователя, весьма специфичной. Посмотрите на то, как это должно выглядеть со стороны пользователя.
Допустим, у нас есть два человека, которые редактируют разные части документа. Одному из них не понравилось последнее изменение, и он нажимает кнопку отмены. Если система поступит так, как делают локальные текстовые редакторы — откатит последнее изменение из истории всех правок, то это вполне может привести к отмене операции другого пользователя. В таком случае оба будут сбиты с толку:
- Тот, кто инициировал отмену, не увидит ожидаемого результата.
- У его коллеги внезапно будет удален только что введенный текст. Ну, или появится удаленный.
Это означает, что уместно отменять не последнюю по времени операцию, а последнюю операцию того пользователя, который инициирует отмену. В таком случае эффект будет более ожидаемым и близким к привычному, который мы можем наблюдать при редактировании локальных документов. Соответственно у каждого пользователя формируется свой undo-redo стек.
Однако в истории операций клиента последней может быть операция от другого пользователя, которую он получил от сервера. Из-за этого становится невозможным применить подход для undo-redo, который используется при редактировании локальных документов: при отмене из стека операций достается верхняя и откатывается. В нашем случае пришлось бы каким-то образом извлечь операцию из «середины» истории и трансформировать все последующие:
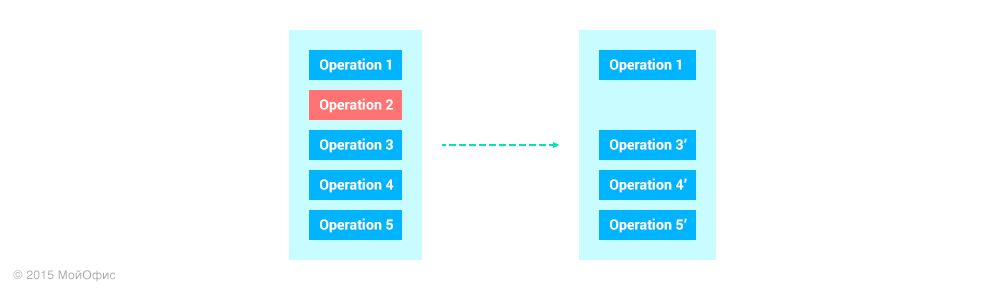
В используемом нами алгоритме важным свойством является то, что операции, которые уже согласованы с сервером, не меняются. И если это свойство будет нарушено, то алгоритм уже не будет работать. Значит, подобный принцип отмены нам не подходит.
Нам необходимо откатить операцию, уже погрузившуюся в пучину истории (стек операций документа). Для этого у нас остается один путь: создать новую операцию, которая будет отменять эффект первоначальной. Мы исходим из того, что для каждой операции можно сгенерировать обратную. Важно, что обратная операция может быть корректно применена лишь к тому состоянию документа, которое возникает непосредственно после выполнения исходной операции.
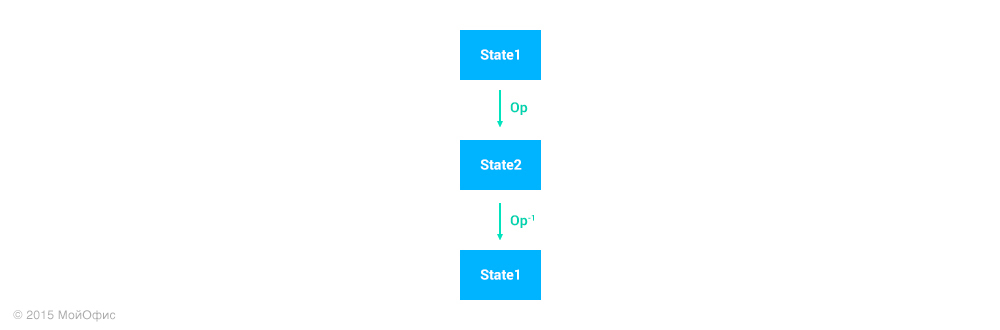
С помощью трансформаций мы можем «перенести» обратную операцию на текущее состояние документа на клиенте, как мы это делали ранее с правками:
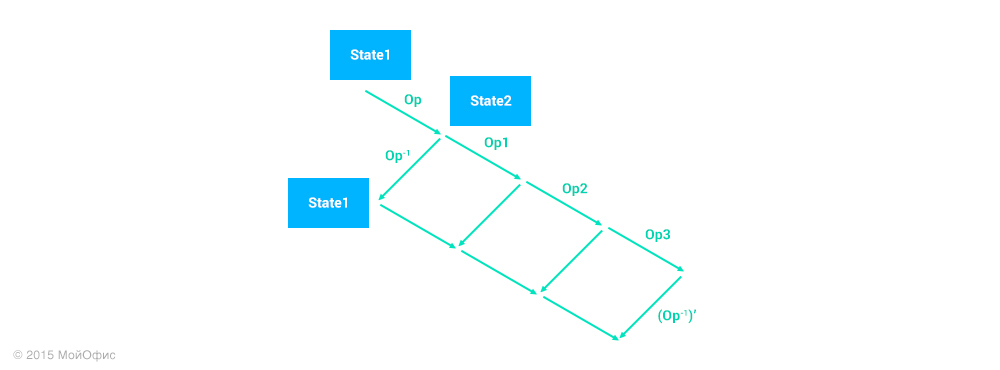
На диаграмме (Op-1)′ — это как раз нужная операция. Больше никаких изменений в существующем алгоритме не требуется: операция применяется локально и отправляется на сервер как любая другая. Ни сервер, ни другие клиенты не могут отличить undo-операцию от обычной. Информация о том, что это была операция отмены, сохраняется только у создавшего ее пользователя, поскольку она нужна для корректной работы redo.
In theory, there is no difference between theory and practice.
But, in practice, there is.
Johannes Lambertus Adriana van de Snepscheut
На данный момент у нас уже есть алгоритм, позволяющий обеспечивать неблокирующее одновременное редактирование с возможностью отмены операций. На этом этапе в большей части теоретических статей предполагается, что задача построения алгоритма решена. В качестве «тестового полигона» используется пример с редактированием одной строки, где операций редактирования всего две: вставка и удаление символа. Иногда приводят пример, где у символа есть какое-то свойство и, соответственно, появляется третья операция для изменения его значения. Я не просто так упоминаю общее количество операций, ведь нам необходимо уметь трансформировать любую из операций относительно любой другой, а значит для N операций нужно реализовать N2 трансформаций. Когда операций две или три, это не представляет проблемы.
На сегодняшний день интерфейс ядра нашего продукта содержит более пятидесяти функций по редактированию документа. Если каждую из них мы представим как отдельную операцию, то нам придется реализовать и оттестировать более 2500 трансформаций, что просто физически невозможно. К тому же мы постоянно добавляем новую функциональность, так что это количество продолжает расти.
Естественным решением в этом случае является отказ от взаимооднозначного соответствия между действиями пользователя и операциями. Набор операций должен быть минимальным, но таким, чтобы с помощью последовательности операций можно было бы описать любое действие пользователя. Причем, если мы хотим максимально ограничить количество операций, сами операции должны быть универсальны. Дело в том, что с точки зрения трансформаций нет разницы между операциями задания цвета шрифта или его размера. Так же как нет разницы между вставкой символа или вставкой абзаца — все это вставка в одномерную коллекцию. В результате получается, что останется три принципиально различных операции: вставка элемента, удаление и установка свойства объекта.
Такие продукты, как CoWord, представляют весь документ в виде последовательного списка разного типа элементов: буквы, переводы каретки, картинки и прочее. И для такой модели документа вполне хватает предложенных трех операций. Но проблема заключается в том, что эта модель не позволяет полноценно представить офисный документ cо стилями, заголовками, колонтитулами и таблицами.
Документ как дерево
Вместо списка естественно представить документ в качестве дерева, отражающего его иерархическую структуру. Упрощенно, документ в этой модели выглядит так:
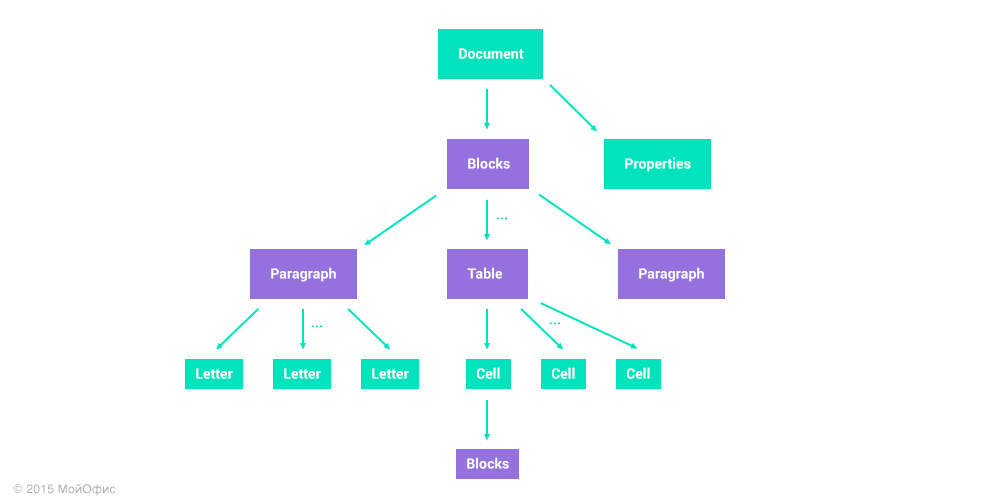
Я заведомо сократил количество типов элементов, чтобы упростить схему, но смысл сохранился. Документ представлен в виде дерева с двумя типами узлов:
- Узлы с фиксированной структурой отмечены зеленым цветом. В качестве примера можно взять корневой элемент. У любого документа в рамках этой модели будет всегда два дочерних узла: список блоков и набор свойств.
- Узлы-коллекции, которые могут содержать переменное количество дочерних узлов, отмечены фиолетовым. К примеру, блоков (параграфов или таблиц) в документе может быть разное количество. Аналогично с буквами в параграфе и строками и столбцами в таблице.
Имея такую модель документа, можно использовать те же три примитивные операции: вставка, удаление и установка свойства. При этом к каждой операции добавляется адрес узла в дереве документа, над которым она выполняется. Для операций вставки или удаления это должен быть адрес коллекции, для установки свойства — адрес узла, у которого мы хотим поменять данное свойство.
Трансформации операций над деревом
Адреса операций помогают нам при трансформациях. Допустим, у нас есть две операции — (Operation1, address1) и (Operation2, address2). Определим то, как влияет взаимное расположение узлов, над которыми они проводятся, на значение Inc ((Operation1, address1), (Operation2, address2)). Всего может быть четыре различных случая:
1. Узлы совпадают, address1 = address2.
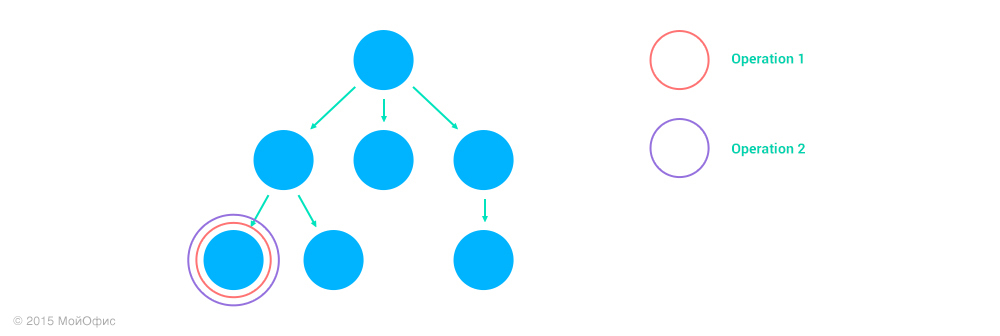
.
В этом случае трансформация проходит так, как если бы документ у нас был плоский. Адрес остается таким же:
Inc ((Operation1, address1), (Operation2, address2)) = (Inc (Operation1, Operation2), address1)
2. Operation2 действует над предком узла Operation1, address2 является префиксом address1.
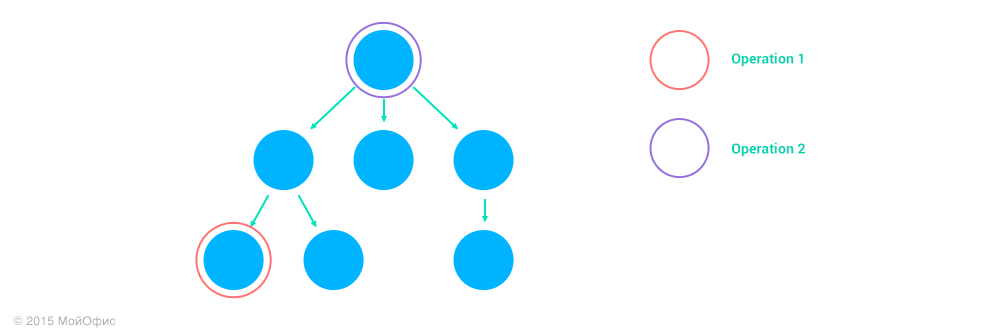
Если Operation2 удаляет предка узла Operation1, то в результате мы получим пустую операцию. Если не удаляет, то сама Operation1 не поменяется, но может измениться ее адрес, если Operation2 меняет коллекцию. Например, если Operation1 — это вставка символа во втором абзаце, а Operation2 — удаление первого абзаца, то в результате получим вставку символа с тем же индексом, но в первом абзаце:
Inc ((Operation1, address1), (Operation2, address2)) = (Operation1, Inc (address1, Operation2))
3. Operation1 действует над предком узла Operation2, address1 является префиксом address2.
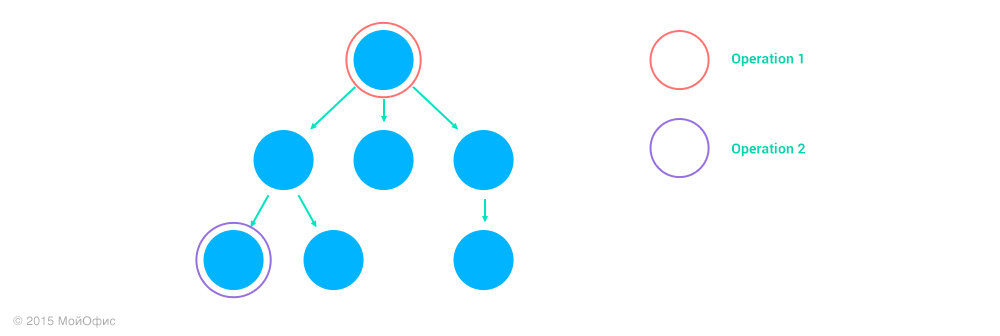
В этом случае Operation2 никак не влияет на Operation1:
Inc ((Operation1, address1), (Operation2, address2)) = (Operation1, address1)
4. Operation1 и Operation2 действуют над различными узлами, ни один из которых не является предком другого.
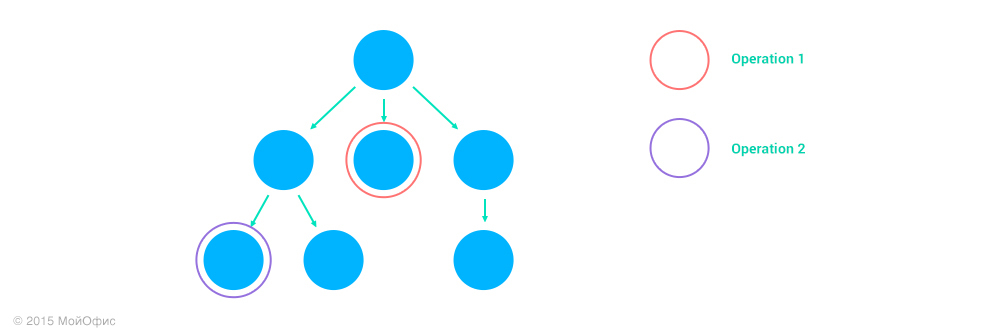
Тут тоже трансформация является тождественной:
Inc ((Operation1, address1), (Operation2, address2)) = (Operation1, address1)
Эти правила позволяют нам получить трансформацию для любой пары операций. Кроме того, операции над различными частями документа трансформироваться не будут, что положительно влияет на производительность.
Двумерные коллекции
Отдельно стоит упомянуть о таблицах. Я встречал несколько публикаций, где авторы рассматривают OT над иерархическим документом. Однако в качестве узлов-коллекций всегда использовались списки. Когда же речь заходила о таблицах, то говорилось, что их всегда можно задать как список строк или колонок, которые в свою очередь являются списком ячеек. Такой подход в корне неверен, поскольку не позволяет корректно взаимно трансформировать операции над строками и операции над колонками. И сейчас я расскажу почему.
Представим, что мы храним таблицу размером 2 на 2 в виде списка строк:
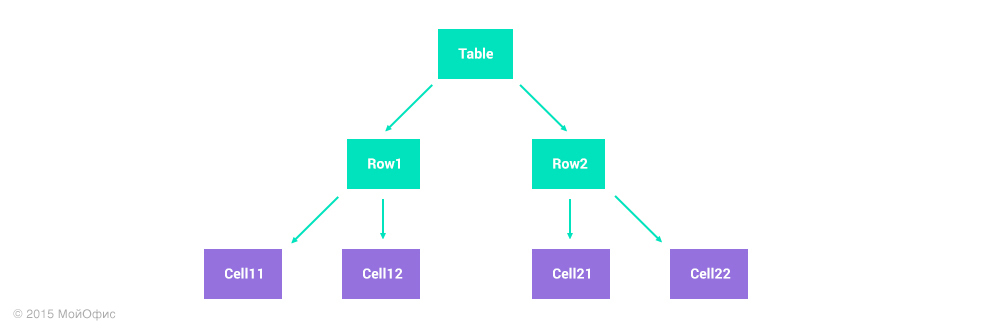
Допустим, один пользователь вставляет строку в конце таблицы, а второй параллельно удаляет правую колонку. У первого пользователя его действие описывается единственной операцией: insert (Table, 3, {Cell31, Cell32}). Второму же понадобятся две операции: remove (Row1, 2), remove (Row2, 2). Если применить все правила трансформаций, описанные выше, то в результате мы получим вот такое состояние таблицы:
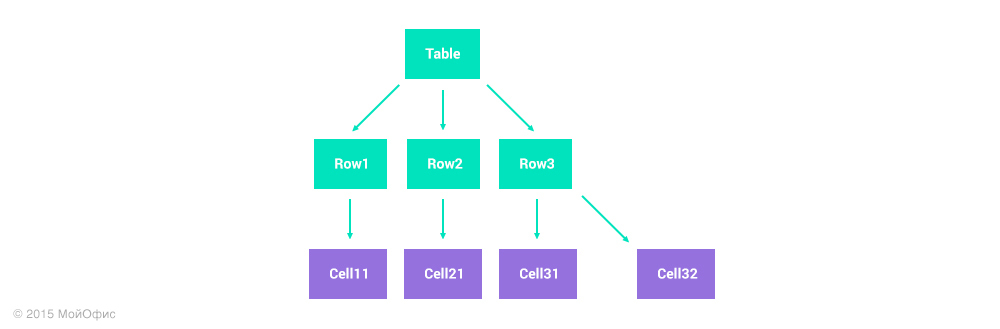
Либо мы допускаем не совсем прямоугольные таблицы, либо находим другой подход. Мы выбрали второй вариант. А точнее, представили таблицы как отдельный, двумерный тип коллекций. В отличие от списка, операций над ними может быть не две, а четыре: вставка и удаление столбцов и аналогичные для строк. И адрес дочернего элемента — ячейки — задается не одним числовым индексом, а парой. Этот подход позволяет корректно представлять и трансформировать операции над строками и колонками и не допускать ситуаций с неправильной структурой таблицы.
На этом хотелось бы выдохнуть и написать, что это все. Для OT невероятно точно подходит фраза «дьявол в деталях», так как сущие мелочи оборачиваются необходимостью решать принципиальные задачи и усложнять алгоритм. Поэтому в реальном алгоритме операций над списками у нас не две, а четыре. Причем одна из них никогда не выполняется. И измениться операция может не только в ходе трансформаций, но и в момент выполнения.
Охватить в этой статье все нюансы уже просто не представляется возможным, и мы оставим их для продолжения, а вторую статью на этом закончим.
До встречи!
