Симулятор машинок Брайтенберга
Просто захотелось написать симулятор машинок Брайтенберга. Корни у этой вещи растут из идей построения простеньких роботов, но также она интересна с точки зрения развития сложных систем.

Итак, что же это такое?
(Осторожно, в статье чрезвычайно много картинок и анимаций!)
Машинка брайтенберга — автомат, на самой простой логике из минимального числа элементов, который, однако, демонстрирует сложное поведение, которое внешний наблюдатель может принять за разумное (простое выглядит как сложное, «понты» роботов).
Их описано 6 типов, на основе некой конструкции под названием нейрод. Нейрод может принимать тормозящий либо ускоряющий сигнал, который влияет на количество импульсов на выходе. Нейросеть таких нейродов (даже самая простая: 2–8 элементов) может создавать несколько базовых моделей поведения. Принцип работы автоматов такой:
Сенсоры (реагируют на свет) → сеть нейродов → актуаторы (моторы)
Первый тип поведения, самый простой — когда нейродов нет и сигнал сенсора напрямую идёт к мотору. Тогда левый глаз крутит левый мотор тем сильнее, чем больше освещён, и тоже самое с правым. Такая система будет «убегать» от света.
Если перекрестить проводники (левый глаз к правому мотору и наоборот) то получим светолюбивого робота, он будет ехать, ускоряясь, к лампочке. О других типах подробнее по мере их моделирования.
Предполагалось (Брайтенбергом) посадить рой таких машинок 6 типов в комнату с лампочками, и тогда наблюдатель (гипотетический роботопсихолог) усмотрит в их передвижениях сложное поведение. Усмотрите ли такую сложность Вы — посмотрим. В статье будет много гифок с симуляциями =)
Пожайлуй сразу покажу такую комнату с несколькими машинками
Белые кружочки — лампочки. Цветные — автоматы разных типов.
Иногда красивее получается демонстрация с траекторией каждого автомата:
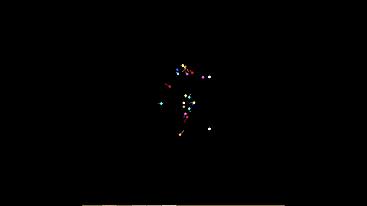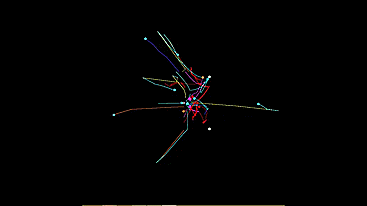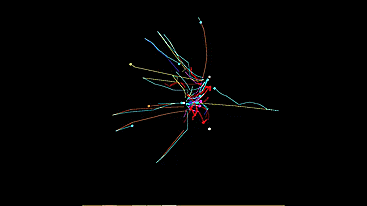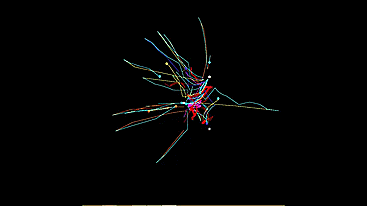
Итак, приступим. Первым я реализовал светолюбивый тип. Всю систему моделировать нет нужды. Сперва мне показалось что я могу просто поделить мощности источников света на на квадрат расстояния до них, сложить векторно и передать автомату полученый вектор «направление к свету» как вектор движения. Но получается совсем не то.
Во-первых — в системе Брайтенберга у машинки есть два светочувствительных элемента. Если они реализованы как направленные сенсоры, то смотрят вперёд, а если как ненаправленые, то не должны различать направления вперёд и назад. Так что я брал плоскость перпендикулярную вектору движения, и отражал «направление к свету», если оно указывало назад. Получились такие уши, которые не различают откуда раздался звук — спереди или сзади, а только справа или слева, и какой силы.
Во-вторых, апарат на колёсиках не может двигаться перпендикулярно вбок, у него есть максимальный угол поворота (за еденицу пройденого расстояния), максимальная скорость и инерция. Это всё я добавил обрезав угол вектор движения относительно вектора направления автоматона под некоторый максимальный, его же обрезав по модулю, и предварительно векторно сложив их: V_new = Inertia * V_old + (1 — Inertia) * LightDir.
...
switch (TypeOfAu)
{
case 1:
calcangle(); //заранее просчитываются cos и sin всех углов
GetLights(); //получаем вектор направления наибольшей освещ'нности
turn(true); //поворот системы координат на угол автомата
{
lightX = Math.Abs(lightX); // отражение векторов которые смотрели назад
SetMod(); // расчёт интенсивности света (модуль вектора света)
if (light > BackToNormalAfterProtectionClarion) Switch("state");
CutMod(); // обрезка по модулю к максимальной скорости
CutAng(ref lightX, ref lightY); // обрезка по допустимому углу поворота
}
turn(false); // возврат в исходную систему координат
break;
...
}
vx = (1 - inertia) * lightX * Vv + inertia * vx;
vy = (1 - inertia) * lightY * Vv + inertia * vy;
// Vv - константа реакции сенсора, переводит количество света в скоростьРезультат:

В итоге стали заметны особенности — к примеру, видно что машинки проезжающие точно посередине между двумя лампочками продолжают движение. Всё хорошо, можем на основе этой создавать новый тип.
Теперь будет боязнь света. Для этого нужно сделать всё тоже, но отразить вектор движения относительно текущей ориентации машинки (не отражение относительно её координаты! Иначе опять получится физически нереальный аппарат).
...
case 2:
...
turn(true); // внутри блока действий в повёрнутой системе координат
{
...
lightY = -lightY; // одна строчка отражения соответсвует перепутыванию проводов левого и правого сенсоров
}
turn(false);
break;
...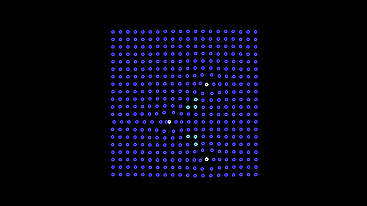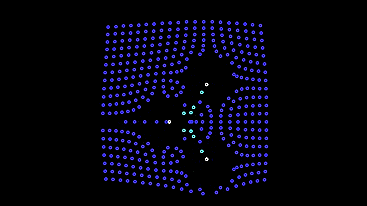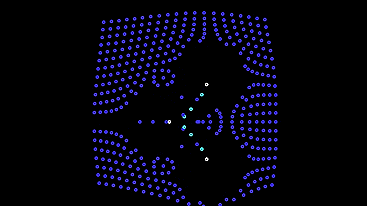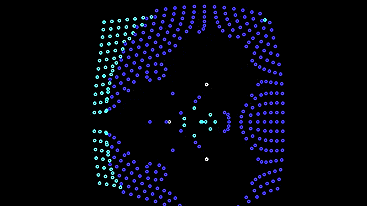
Единственный минус — такие автоматы убегают с экрана и оставляют за собой пустое поле. Поставим им защитный механизм от убегания — при низком освещении они будут менять своё поведение на первую модель, пока не вернутся к лампочкам.
Настроим теперь машинки с парой нейродов. Первая будет повторять модель светолюбивой машинки, но со встроеными нейродами на линиях. С сенсора будет идти тормозящий сигнал на нейрод, а с нейрода сигнал пойдёт на мотор. Теперь чем больше светим на сенсор, тем меньше сигналов к мотору — тем медленнее едет машинка. Такая система будет иметь проводку как первая модель, но вести себя больше подобно второй — убегать от света. Но если у первой с удалением от источника падала скорость, то эта наоборот: будет ускоряться. Поправим код для вычисления модуля вектора движения соответствующим образом и вуаля:

Когда я сделал эту машинку в первый раз мне показалось что она работает правильно, но что-то было не так… Вот это первая версия, где я перепутал какой-то знак.

Красивее за ними наблюдать в режиме записи треков — они рисуют что-то вроде глаза.

Теперь следующая машинка. Опять перекрестим провода, но уже с нейродами на них (в коде — уберём последнее отражение вектора):
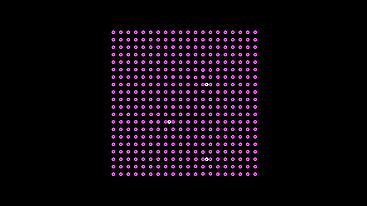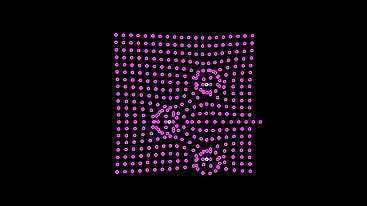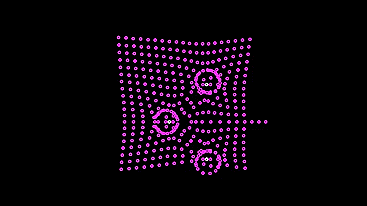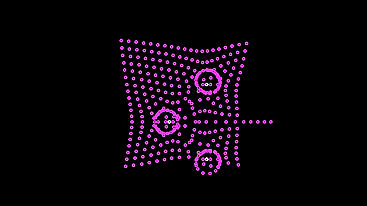
Эта машинка более мудрая, она не ломится к свету, рискуя разбить лампочку (а в реальной модели так и было бы), а останавливается поодаль, когда на сенсоры попадает достаточно света, чтобы тормозящий сигнал полностью остановил генерацию сигналов для мотора.
Номер пять. Машинка со сложной системой нейродов. За описанием можно посетить эту статью, а я пока расскажу как это делается простыми способами — добавляется барьер по количеству света, и меняется знак в операции отражения в зависимости от того выше порогового значения уровень света, или ниже. Реальная машинка должна убегать как третья, когда света мало, и ехать на свет как четвёртая, когда его много. Где-то будет ещё и внутренний круг, где она будет совсем останавливаться — я долго подбирал коэффициенты, часто менял их, но красивого убегания от «кромки света от костра» так и не добился. Всё равно внутренний круг остановки должен быть достаточно широким (занимать больше половины площади) — это связано с реализацией квадратичного затухания уровня света с увеличением расстояния, так что виновата физика, не я =)

И последняя. Эта должна менять свои модели по противоположному принципу — тянуться к свету когда его мало, и убегать когда много. Почитатели Азимова сразу поймут что такая машинка будет постоянно бегать по кругу на эквипотенциальной линии (линии постоянного уровня освещённости). И если продолжить прямую «безсенсорную» модель, которую я использовал до сих пор, то машинка будет просто доезжать до этой линии и останавливаться. В реальном мире её бег по кругу будет связан с тем что один из глаз находится внутри круга, а другой снаружи, и внутренняя нейродная структура создаст для алгоритма движения новый кейс — заставит двигаться перпендикулярно направлению на свет. Чтобы симулировать и этот тип автомата, мне пришлось добавить настоящее описание двух сенсоров, и чтобы на одном из них значение освещённости в какие-то моменты оказывалось ниже порогового, когда на другом — выше, нужно было разместить их на некотором расстоянии. Физическое расстояние между сенсорами называют паралаксом (например между глазами человека, или двумя телескопами в одной системе). Вот машинка после моих допилов (глаза на гуи не рисовал).

...
case 6:
calcangle();
double paralax = 0.01;
GetLights((angless) * paralax, (anglecs) * paralax);
SetMod();
double tempL = light; // значение интенсивности света в одном глазу из глобальной переменной переносится в темп - временную
GetLights((-angless) * paralax, (-anglecs) * paralax);
double CicleMaxSpeed = 4;
int sw = 0;
SetMod(); //после второго сетмода получаем два значения интенсивности света - одно в глобальной и одно во временной переменных, это значения на левом и правом глазу
...Изменение паралакса приводит к изменению точности

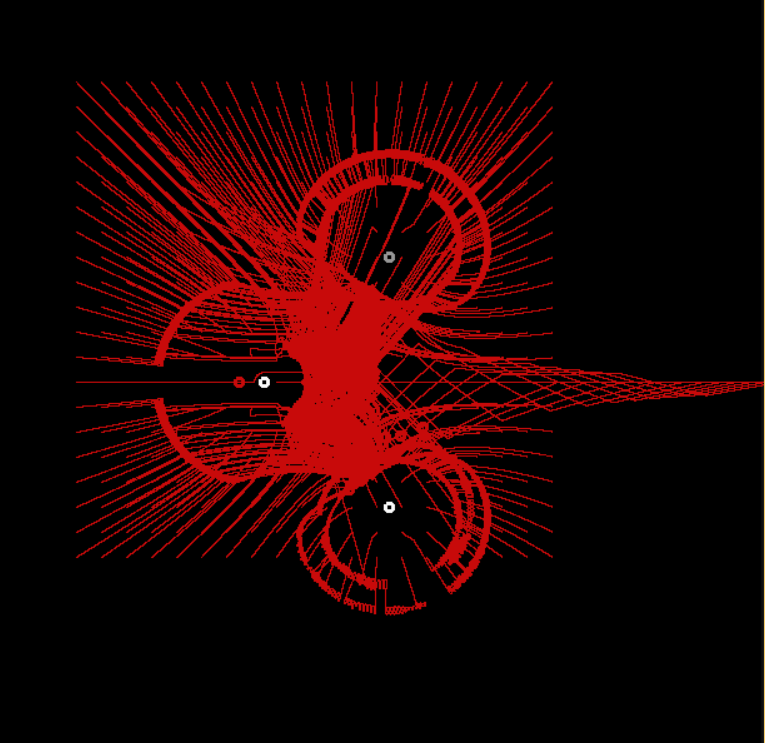
При некоторых значениях автомат движется почти по ровным дугам, при других — по волнистым траекториям, постоянно то приближаясь то отдаляясь. Похожее поведение у роботов в гонке по линии.
Теперь закинем семейство из разнотипных автоматов на поле.

Первая версия в начале статьи мне показалась несколько скучной, поэтому я сначала заставил некоторые лампочки время от времени гаснуть и зажигаться… А затем и вовсе — сделал перемешивающий алгоритм, который раз в какое-то время меняет тип машинки на какой-то другой, с тем чтобы она прошла «все воплощения»:

Без всего этого можно посмотреть на сетку всех типов на одном поле.

После этого я задумался о том, чтобы у машинок был физический размер (чтобы они не проходили друг сквозь друга), но расчёт коллизий — задача тяжёлая для компьютера, тем более с таким большим количеством участников, поэтому я просто сделал пару снимков и отключил режим

В принципе, в нём было всё тоже самое, только машинки толкались вокруг их ассимптотических траекторий, а не находились точно на них, вот и всё. Вернёмся в мир без коллизий)
Рассмотрим теперь систему на длинной выдержке — к чему она стремится?
Режим переключения лампочек не позволяет системе остаться статической картинкой, но светолюбы очень постарались — они прицепились к своим лампам и не успевают от них отбежать в период когда они выключены.
Их более мудрая версия — успевает, и в итоге есть стайка, которая движется по циклической траектории между тремя лампами.
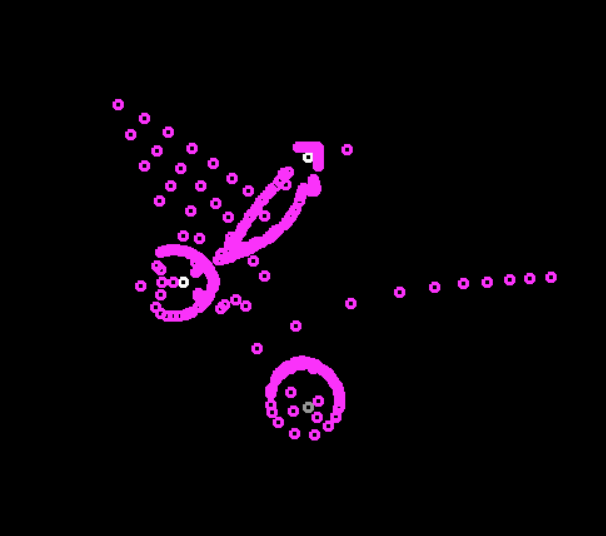
Светобоязливые работают иначе. Так как система защиты возвращает их с той же скоростью что и их скорость удаления — на каждом уровне, то они формируют ровный шум, примерно половина автоматов неспешно удаляется, другая половина возвращается в защитном режиме.

С их прокачанной нейродами версией дело обстоит иначе — они быстро разлетаются, но медлено собираются назад. Я ожидал что они в итоге сформируют ровный сужающийся круг, но нет. Они сохраняют несимметричную форму, и дают иногда красивые картинки

Иногда похожи на такой же хаос:

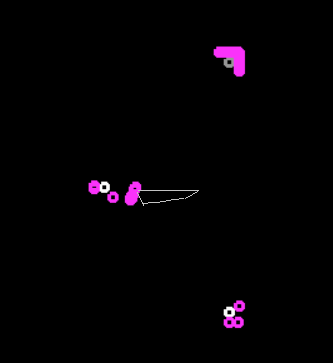
Меняющийся автомат чаще всего ведёт себя так же. Но в итоге они сбиваются в очень маленькие группы, которые достаточно кучно ездят от лампочки и к лампочке по вот таким рельсам.
Кроме нескольких автоматов, которые поймали «свою волну» и крутятся в правой части комнаты. Я ждал пока они примкнут к одному из трёх кланов, однако за 2 часа симуляции этого так и не случилось, похоже это тот самый случай странных динамически стабильных траекторий, как у того астероида, который облетает гравитационный колодец земли то справа то слева.
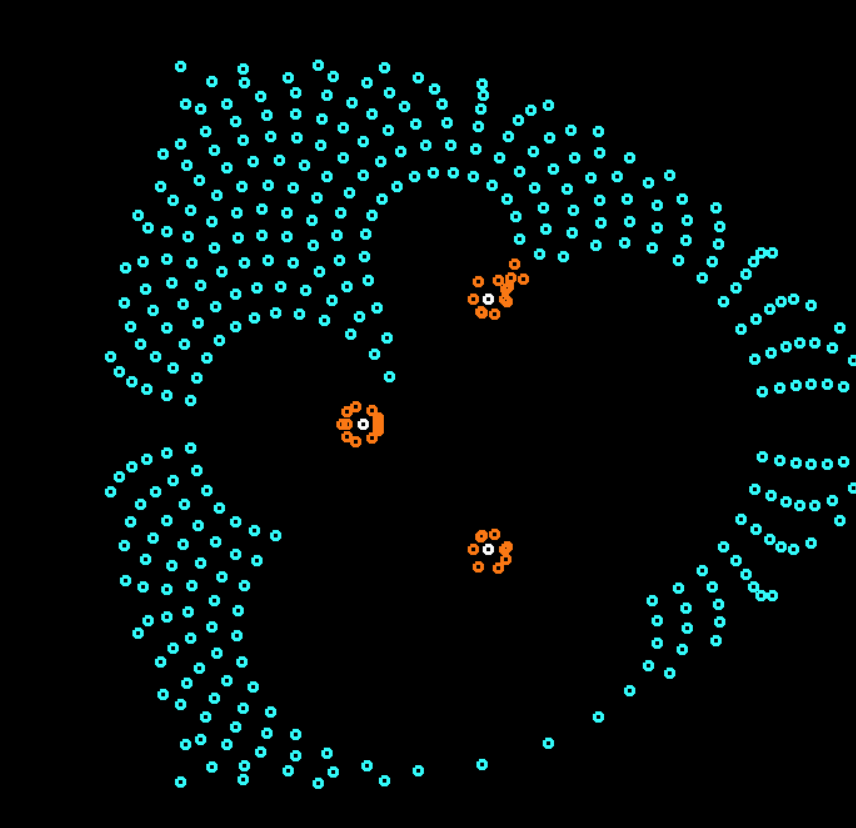
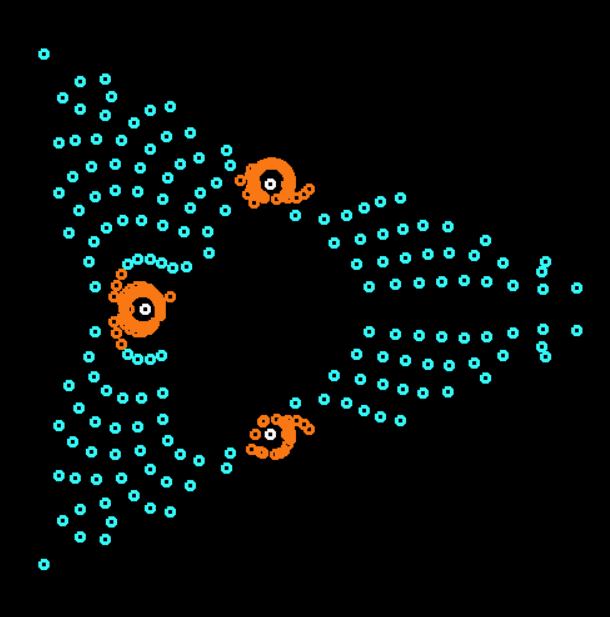
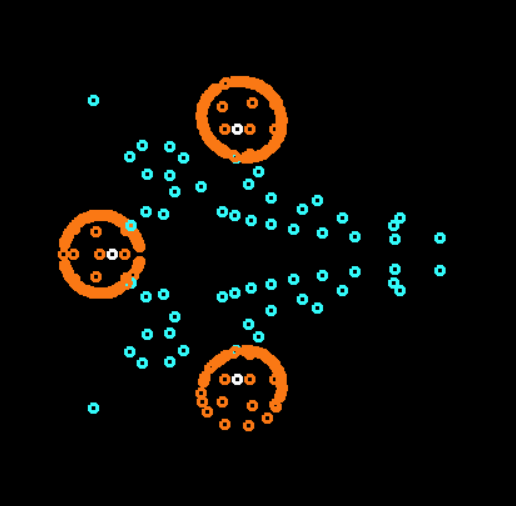
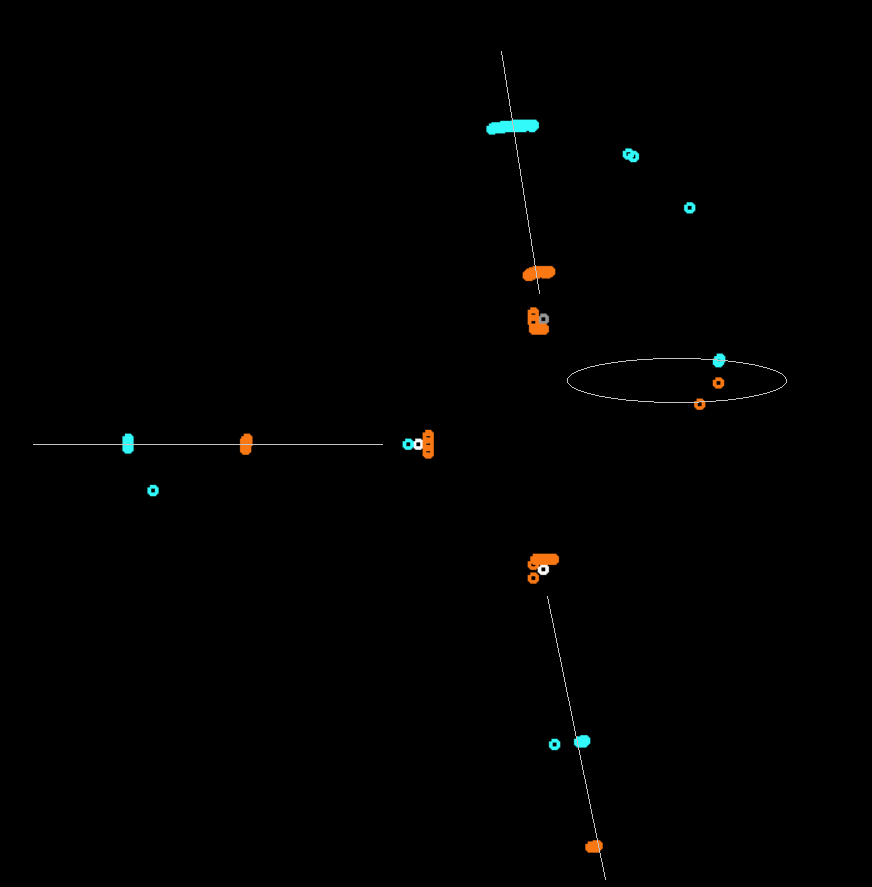
Циклические автоматы показали телефонную трубку (или улыбающуюся рожицу?), сбились в кучу, и стали сворачивать и разворачивать щупальца по очереди к работающим в данный момент лампам.
Рожица
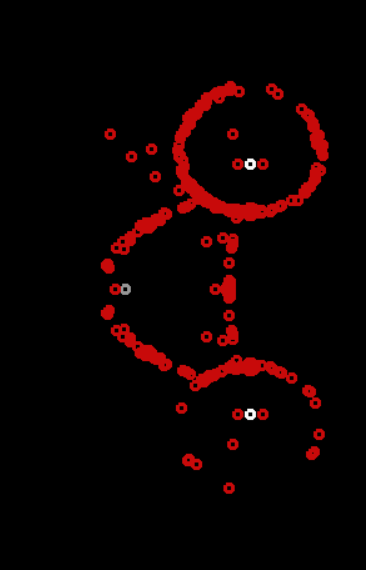
Стабильный режим

Тем временем, пока шли долгоиграющие симуляции, я подумал над другими вариантами и добавил ещё три нестандартных типа. Они ориентируются не на свет, а на другие автоматы.
Первый из них ждёт пока в окрестности появятся автоматы, и пытается следовать за ближайшим из них. В остальное время стоит и грустит.
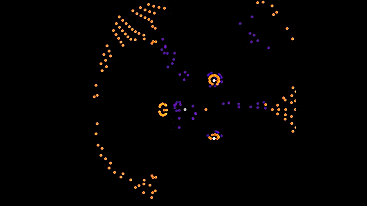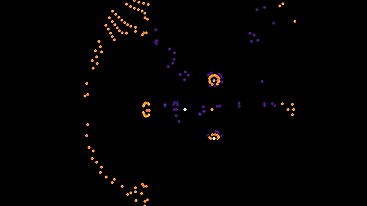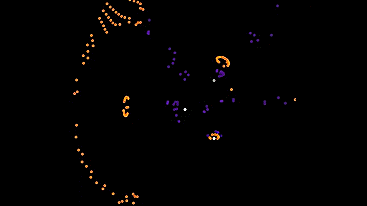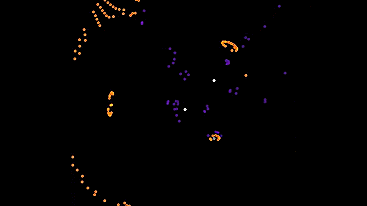
Можно назвать их собаками, потому что им нужен хозяева. Я поместил их на поле вместе с 5ым типом, иначе они бы все просто стояли.
Ещё один тип — усредняет координаты многих автоматов и бежит в толпу — «экстраверт».

Его антипод — интроверт, который пытается держать дистанцию.

В начале решётка имеет трансляционную симметрию и центральным автоматам некуда идти — в любую сторону они бы приближались к соседям, так что они ждут пока разбегутся крайние. Интересно это выглядит в режиме треков — мохнатая микросхема получается.
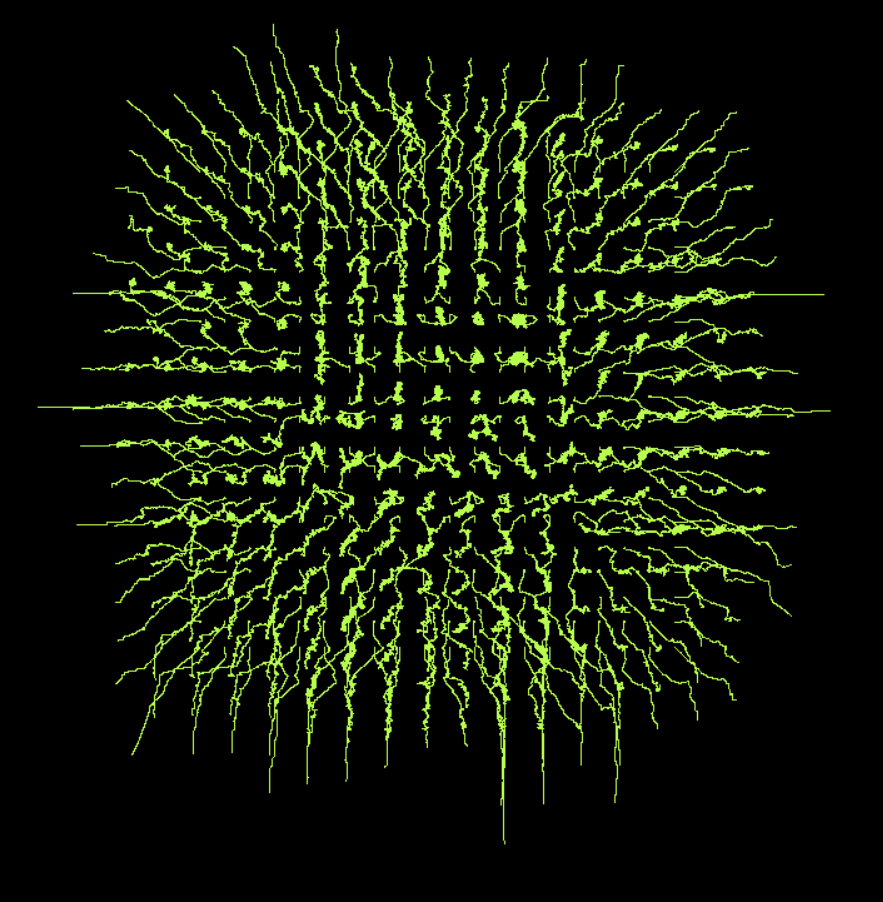
Теперь поместим все 9 типов (включая новые) и посмотрим на сетку. (перемешивание типов включено)
А в режиме треков они рисуют одуванчик

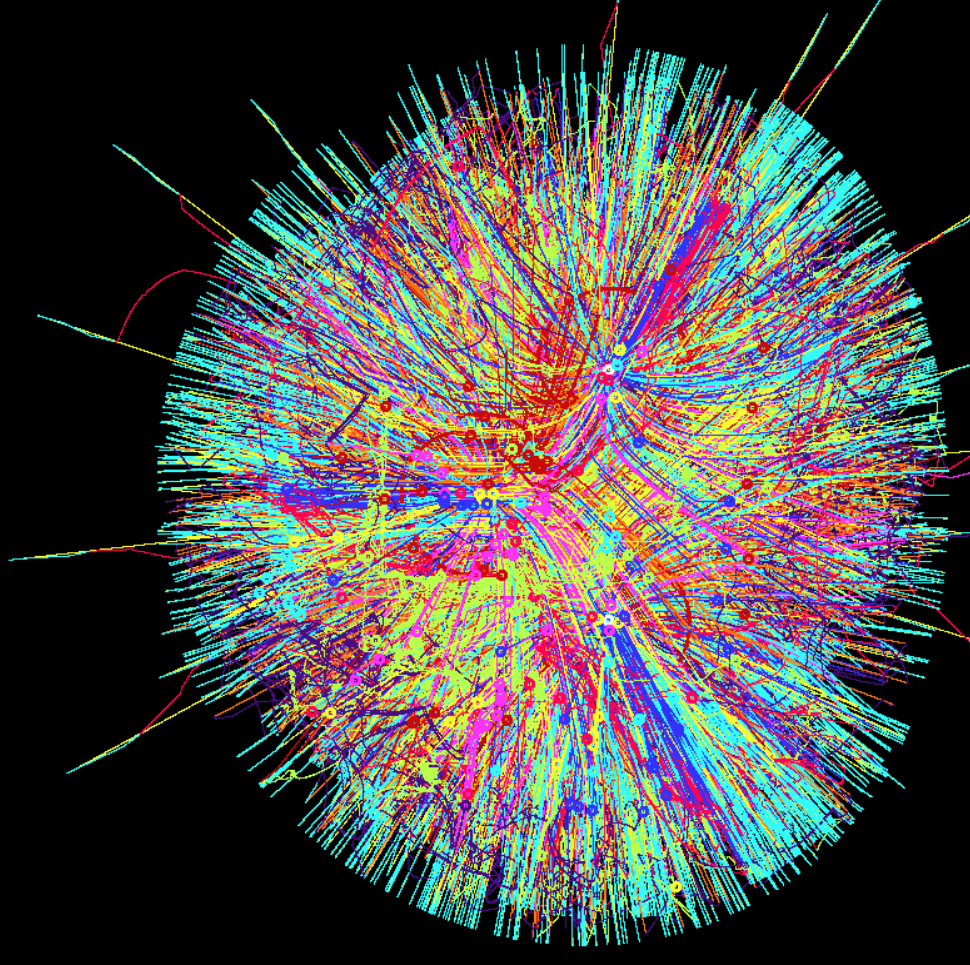
В центр я поместил источник света с отрицательным значением мощности. Не знаю, чего я ожидал, но антисвет хоть и приманивает обычно убегавших автоматов, но их поведение не становится похожим на «перекрещенные» аналоги светолюбов, а получается что-то третье, более сложное.
Ещё одуванчики, которые получились.




Так тоже получается одуванчик. Я заинтересовался, увидев отрисовку «паутинки» в уголке одной из симуляций — вдаль лучами уходили один за другим беглецы, а собаки за ними не успевали, и переходили от одного к другому вогнутыми полудугами. Подумал, что если сделать так массово, то получится паутинка, как её всегда рисуют. Поэтому закинул в комнату только эти два вида автоматов —, но что-то пошло не так. В любой конфигурации система неустойчива и собаки заваливаются в какую-то сторону, в итоге выходит просто ещё один одуванчик — и никакой паутины.

Добавил ещё одну лампу.


А вот… Эм… Дикобраз?

В общем, поведение, как на мой вкус действительно достаточно сложное. Но двинемся дальше. Попробуем показать нелинейность. Для этого хорошо подходит разбегающаяся версия. Расходимость от сферы (которой является эквипотенциальная по освещённости поверхность вокруг лампочки) почти гарантирует появление детерменированого хаоса.
Запустим такую же сетку, но очень маленького размера — чтобы начальные условия для машинок различались лишь чуть-чуть (автоматы выезжают почти из одной точки), и посмотрим как система разовьётся и что нам покажет.
Теперь запустим такую же маленькую сетку, но с машинками разных типов и включенным перемешиванием типов

Такие вот интересные картинки получаются… Для разнообразия можно сменить модель визуализации, скажем, соединить все машинки линиями (как будто бы они бы натягивали одну длинную нитку). Так удобнее наблюдать за тем как именно алгоритм комкает изначально ровную сетку машинок, и куда он отправляет разные её части — как они мигрируют по своему миру.
Получаются залипалки вроде той что в медиаплеере.
Иногда появляются интересные фигуры.



В общем, такой вот симулятор. Не стесняйтесь предлагать свои идеи и предложения в комментариях, что ещё можно добавить, или какой эксперимент поставить. Лично я считаю получившуюся штуку удобной демонстрацией для теории нелинейных систем — в ней можно искать ассимптотику, расходимости, любопытные паттерны, показывающие сложность простых систем… Людям может пригодится концепт как в автоматизации, так и начинающим в построении BEAM роботов — чтобы понять суть, ну и вообще — посмотреть цветные картинки.
Всем добра, роботопсихологи. Это всё.