Simulation theory: взаимосвязь квантово-химических расчётов и Реальности14.12.2018 12:49

Введение

О чём этот текст

Если человек услышит о «симуляции реальности», то в наиболее вероятно ему в голову придут или разные научно-фантастические произведения (типа Матрицы, Темного города, или Теоремы Зеро), или компьютерные игры. В случае людей, чьи головы засорены инженерным образованием, возможно всплывут пакеты типа КОМПАС-3D AutoCAD, Solid Edge или NX. Человек, слушающий научпоп, возможно вспомнит о всяком моделировании разных космических штуковин.

А ведь есть ещё один уровень реальности, который окажется незаслуженно забытым: тот, на котором происходит вся химия — это уровень атомов и молекул. Его тоже можно вполне успешно моделировать на компьютере. Поскольку в данном срезе реальности всем заведует квантовая механика, то подобные расчёты часто называют квантовой химией. И вот о её связи с Реальностью, изучаемой экспериментальными методами, мы и поговорим.

Этот текст будет об элементарнейших вещах. Но, практика чтения научных журналов и слушания различных докладов показывает, что об этом надо постоянно напоминать.

Текст рассчитан на людей понимающих и/или интересующихся тем, как живут атомы и молекулки.

Взято из https://xkcd.com/1791/

Краткая предыстория

Так случилось, что собрат по несчастью работы в российской науке предложил мне прочитать лекцию на своём спецкурсе для 2-х человек в одном из известных физических ВУЗов России. Но, по странному стечению обстоятельств её перенесли на проходившую параллельно студенческую конференцию… Там она особого интереса у студентов она не вызвала, а материал мне было очень-очень жалко, поэтому решил немного заспамить Хабр, попробовав превратить учебную лекцию в научно-популярную статью.

Физические методы исследования жизни молекул

Мы знаем из школьных курсов химии и физики, что все вещества состоят из атомов, молекул, ионов, или их комбинаций. И мы, вроде, даже знаем какой жизнью они живут. Но у этой инфы должны быть свои надёжные источники (методы исследования), и они действительно есть.
Таких способов подсмотреть за жизнью атомов существует очень и очень много. Желающие, например, могут ознакомиться с некоторыми из них поподробнее в классических учебниках
— Пентин Ю.А., Вилков Л.В. Физические методы исследования в химии. — М.: Мир, 2006,
— Драго Р. Физические методы в химии. — М.: Мир, 1981.
Но, грубо и достаточно легко выделяются 3 основные группы методов:

спектроскопические методы,
дифракционные методы,
различные методы микроскопии (не важно, просвечивающей или сканирующей, для нас это сейчас не существенно).

Про последнюю речи не будет, но её инструментарий не менее важен, чем у первых двух.

Почему не будет речи о микроскопии

(просто я в микроскопии не шарю от слова совсем)

Спектроскопические методы исследования вещества

Эта мощная группа методов обеспечивает нас очень и очень многим: от поиска и определения молекул в межзвёздной среде и на других планетах до банальной проверки на взрывчатые вещества в аэропорту.

Общий принцип работы спектральных методов

Когда говорят о спектроскопии, обычно имеется в виду следующий общий принцип работы.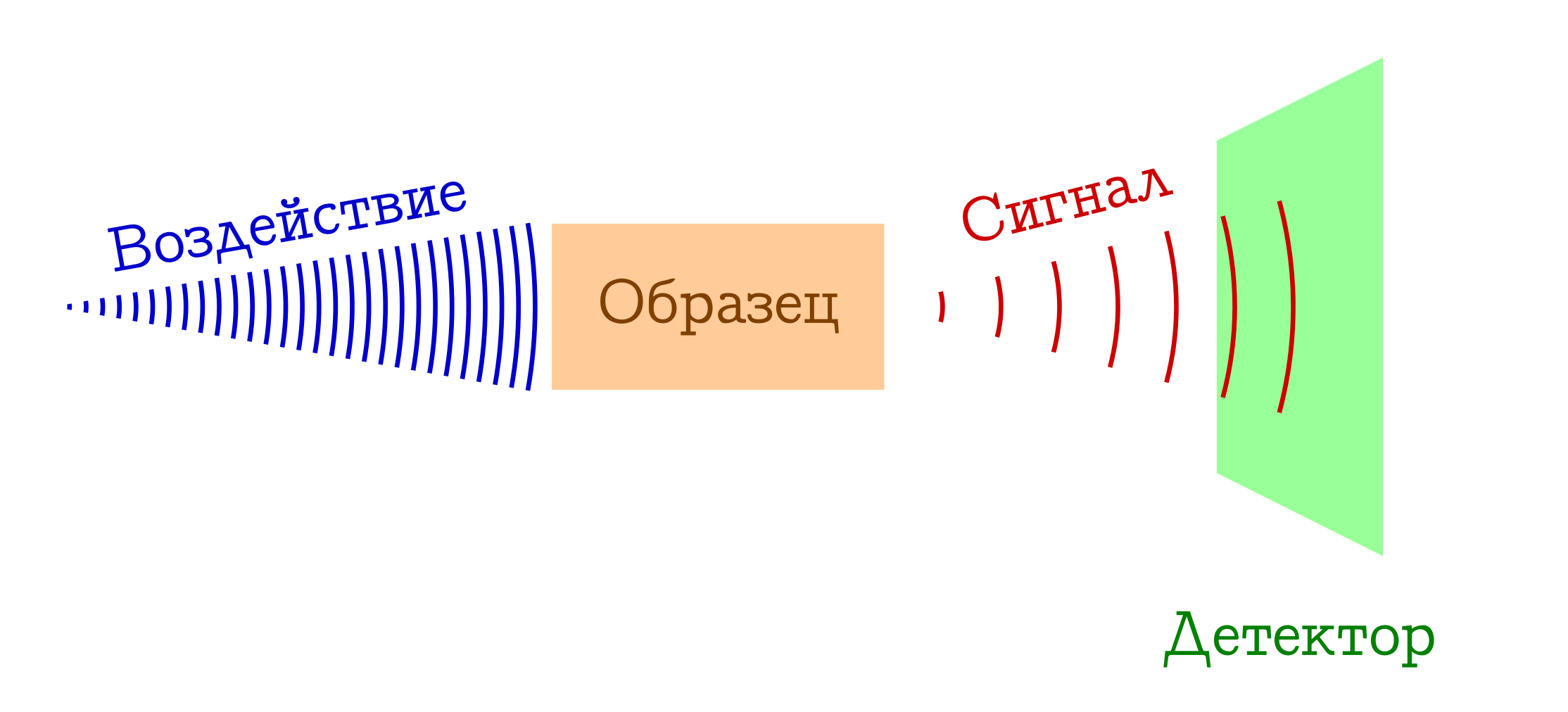

Общая схема спектральных методов исследования вещества

У нас есть нечто, чем мы (например, лампочкой/лазером/солнечным светом) воздействуем на интересующий нас образец. Чаще всего это электромагнитное изучение, но этим вполне могут быть электроны (например, в масс-спектроскопии с ионизацией электронным ударом) или коктейль всего возможного и невозможного из плазмы (например, в спектроскопии пламён, так любимой школьниками и студентами младших курсов химфаков). Так или иначе, на наш образец что-то должно подействовать.
С образцом при воздействии происходит нечто такое, что он меняет своё состояние. Это может быть переход на какой-то возбуждённый уровень (в любой спектрофотометрии или спектроскопии комбинационного рассеяния), или вообще развал молекулярной системы (как в масс-спектрах или фотоэлектронной спектроскопии). Но так или иначе образец в какой-то момент должен быть другим.
???
PROFIT!!! Мы регистрируем некий сигнал (испущенный или поглощённый) при этом изменении образца на молекулярном уровне. Это могут быть потерянные фотоны, затраченные на изменение образца (тогда имеем абсорбционную спектроскопию), или же наоборот, лишние фотоны, испущенные после предварительного возбуждения вещества (эмиссионную спектроскопию), изменение длины волны изначальных фотонов в результате взаимодействия с веществом (спектроскопия комбинационного рассеяния, более известная за рубежом как раменовская рамановская), ну или тупо осколки изначальных молекул (как в масс-спектрах или фотоэлектронной спектрскопии). Вариантов много — суть одна: сигнал есть!

В качестве примера подобных методов можно привести кучу разных буквочек:
NMR, ESR, MW, THz, IR, UV/Vis, XRF, MS, PES, EXAFS, XANES и т.д. и т.п.
Все (или многие из них) знакомы (или должны быть знакомы) каждому химику. Все эти методы — это (далеко неполный) стандартный арсенал уважающего себя исследователя, имеющего дело с веществами.

Спектральные диапазоны и их связь с жизнью молекул

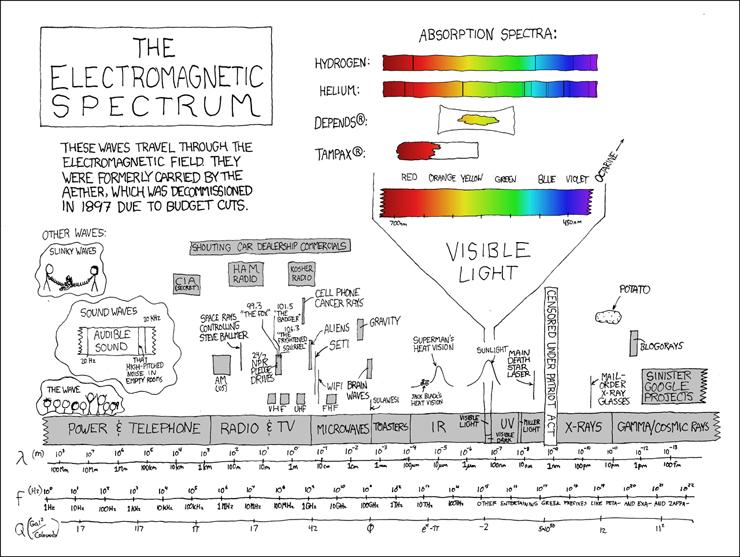
Взято из https://xkcd.com/273/

Поскольку в подавляющем числе случаев спектроскопия всё же завязана на электромагнитное излучение, то логично привязать диапазоны электромагнитного спектра к различным аспектам атомно-молекулярной жизни. Ведь частота используемых в спектроскопии электромагнитных волн является своего рода «часами», позволяющими засечь, сколько длится тот или иной процесс в молекулярных системах. А значит, меняя эту частоту можно изучать (и даже воздействовать) на разные молекулярные процессы.

Итак.

В сверхдлинноволновом диапазоне с химической точки зрения ничего интересного не происходит, так что о нём можно не вспоминать.
С частотой радио- и микроволн (и даже длинноволнового инфракрасного излучения, ИК=IR) вращаются разные молекулы в газовой фазе: большие и тяжёлые — в области радиоволн (более низкие частоты), а маленькие и легкие — в ИК (более высокие частоты).
В ИК же (в основном) происходят различные колебания молекул: всякие конформационные и другие не очевидные движения внутри молекул — в длинноволновом ИК, а валентные колебания (растяжения — сокращения длин химических связей) — в коротковолновом (до 4000 см–1).
Ну, а дальше идёт место спектра, где обитают разные электронные переходы (вплоть до области γ-квантов). При меньших частотах (видимый, УФ=UV и мягкий рентген) живут в основном переходы, связанные с валентными электронами.
Почему мы видим?
Кстати, именно, из-за электронных переходов мы и можем видеть: в наших глазах (в колбочках) содержатся структуры, имеющие в составе ретиналь. При поглощении фотона видимого цвета этой молекулой, в ней происходит разрыв двойной связи, что приводит к цис-транс изомеризации. И именно это изменение воспринимается нами как первичный сигнал, который далее передаётся в наш мозг.

Но при повышении энергии фотонов (т.е. при повышении частоты, как мы помним по формуле Планка $E=h\nu$ ) мы добираемся до всё более и более глубоких слоёв электронной структуры, пока не упираемся в рентгеновском диапазоне до финальных 1s-оболочек (или, как их зовут рентгенщики, K).

Так вот, выбирая правильную длину волны электромагнитного излучения, мы можем посмотреть подробнее на тот или иной процесс в молекулах.

Дифракционные методы исследования вещества

Теперь немного поговорим о дифракции. Принципиальная схема подобных экспериментов тоже проста.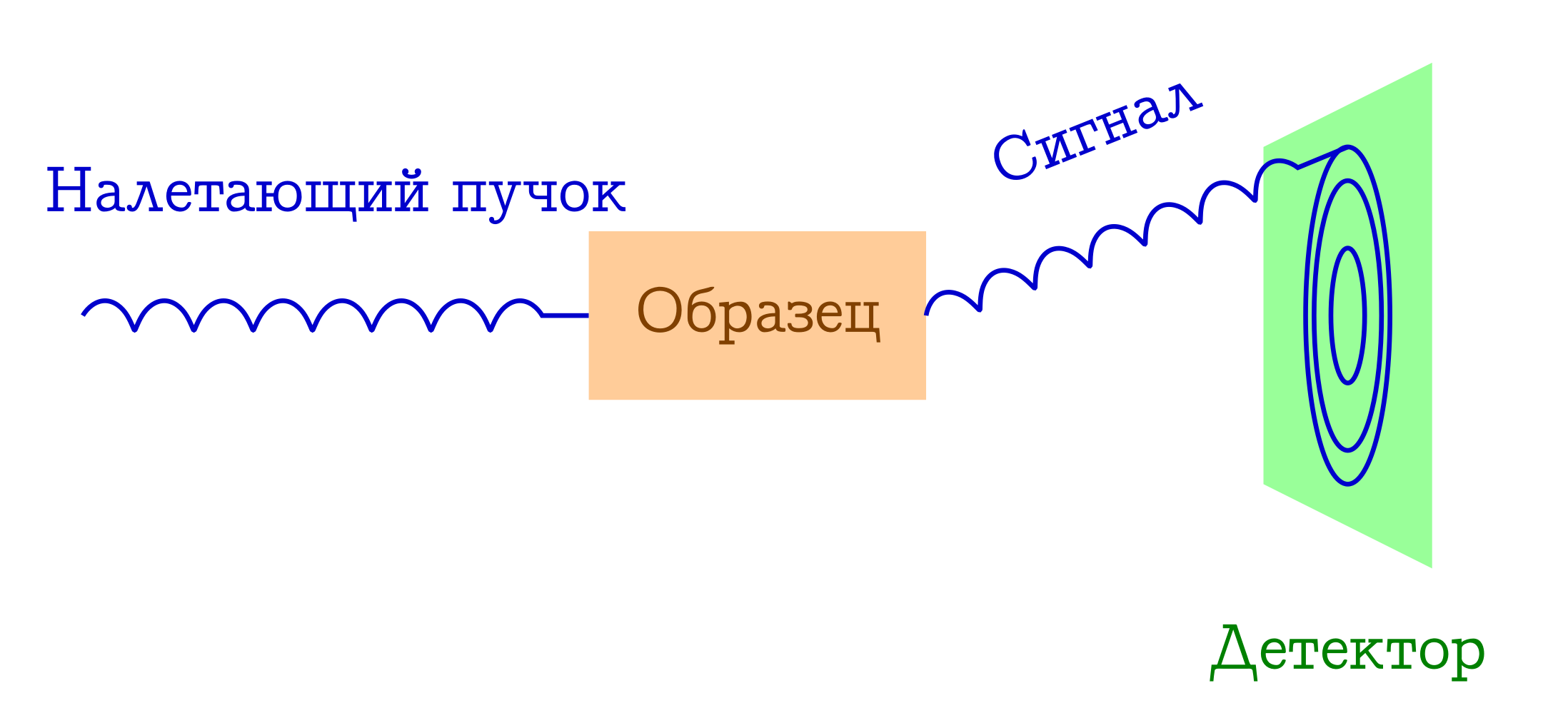

Общая схема дифракционных методов исследования вещества

На образец налетает пучок каких-то частиц. Чаще всего это или рентгеновские фотоны, или электроны, или нейтроны.
Эти частицы по разным механизмам упруго рассеиваются на атомах в интересующем нас образце (т.е. без изменения длины и фазы волны, просто меняют направление своего полёта). С самим образцом от этих налетевших частиц ничего не происходит: он просто не успевает на них среагировать.
Межатомные расстояния служат в качестве дифракционной решётки для налетевшего пучка, поэтому в результате на детекторе мы увидим красивую дифракционную картинку.

Из последнего пункта появляется условие на длину волны налетающих частиц (λ): она должна быть того же порядка или меньше, чем характеристический порядок межатомных расстояний, поэтому типичные λ для данных методов составляют 1 — 0.01 Å.

Основные типы ошибок при сравнении экспериментов и теоретических расчётов

В итоге мы имеем очень интересную картину: и в спектроскопии и в дифракции мы наблюдаем какой-то левый сигнал, который как-то косвенно свидетельствует о том, что происходит в молекулярной системе на самом деле.

Аналогия с платоновской пещерой

Картина эта до жути напоминает миф о пещере Платона. У нас есть некий Реальный Мир Молекул. Но мы видим только лишь тени от него на стенке пещеры (детекторе), которые являются неполным отображением всех интересных вещей, происходящих на этом уровне Реальности.

Но, по счастью, иногда мы можем теоретически рассчитать интересующий нас сигнал (как, например, в микроволновой, ИК или UV/Vis спектроскопии), а иногда мы можем из наблюдаемого сигнала извлечь интересующие нас величины, доступные для квантово-химического расчёта (например, расстояния между атомами в молекуле, дипольный момент и т.д.). И тут у нас возникает шанс, что численный и настоящий эксперимент могут объединиться в страстной стадии сравнения друг с другом… и здесь стандартно могут возникать 4 типа ошибок.

Внимание! Термин «ошибка» здесь означает не то, что результат сравнения заведомо получается неправильный. Просто почва для сравнения становится очень зыбкой и болотистой, и один неаккуратный шаг может легко запороть всю работу.

Разные условия эксперимента и/или расчёта (агрегатное состояние, температуры, давления и т.д.). Мы можем внезапно начать сравнивать между собой разные системы, по какой-то причине считая их одинаковыми. Например очевидно, что добавление одной или пяти чайных ложек сахара к чашке чая приведёт к одной и той же физической системе под названием «чай с сахаром», но свойства у этой системы будут очень разные. И это можно легко измерить. Например, термометром (замерив температуру чая сразу после растворения сахара) или языком (одним из т.н. органолептических методов анализа). Так что сравнивая полученные системы между собой (будь это реальная чашка сахара с чаем, или её компьютерная модель) надо не забывать, что сходство имеет свои границы, и что если мы уменьшим допустимую погрешность для «схожести», то в итоге отыщем различия.
Разный физический и/или математический смысл параметров (у параметра физического смысла в привычном смысле может вообще не быть). Тут тоже всё просто: если мы сравниваем 2 величины с похожим названием, то это не означает, что величины имеют один и тот же физический смысл. Например, рейтинг депутата среди всего населения города vs. рейтинг только среди бабулек. И то и то рейтинг (что бы это ни было), эти числа (или что это там) могут даже сильно коррелировать между собой, но смысл у этих параметров всё равно разный, и эту разницу можно обнаружить.
«Случайные» погрешности. Тут имеются в виду и некие систематические ошибки, о которых не известно экспериментатору/симулятору-теоретику, или действительно случайные ошибки в эксперименте/расчёте, которые невозможно контролировать и/или предсказывать. В принципе подобные вещи могут сами становиться предметом исследования различных интересных систематических эффектов

, или же просто оценка полезнейшего соотношения S/N («сигнал/шум»).
И последней стандартной ошибкой является произрастание рук экспериментатора/расчётчика из тазовой кости, то бишь обычные человеческие ошибки. Тут исследовать ничего не надо, достаточно перепроверить работу или повторить произведённый эксперимент, чтобы обнаружить и устранить соответствующий косяк.

О последних двух типах ошибок ничего более конкретного сказать нельзя, но вот про первые две, да если взять конкретный метод исследования, наговорить можно очень много чего. Поэтому на них и сконцентрируемся. Основной упор при этом мы будем делать на структурных различиях молекул.

Ошибка #1. Различия молекулярных свойств в разных условиях

NaCl: когда ошибок не возникает

Вот почему-то никому не приходит в голову сказать, что у монокристалла поваренной соли (NaCl), представляющей из себя огромную молекулу из ионов Na+ и Cl–, и у двухатомной молекулы NaCl, получаемой испарением этого кристалла при бешеных температурах, одна и та же, скажем структура.

И даже если мы предположим, что хотя бы расстояния между хлором и натрием (rNaCl) и там и там одинаково, то эксперимент нас поставит на место:

Где мы делаем ошибку

На самом деле при таком сравнении мы допускаем возможность Ошибки #2, но тут всё нормально, если мы оценим погрешности подобного сравнения, то они будут порядка 0.01 Å, что существенно меньше разности сравниваемых параметров. Т.е. это не погрешность, а реальный эффект.

Как самому получить расстояние между катионом натрия и анионом хлора в кристалле поваренной соли

Получение расстояния между атомами в двухатомной молекуле NaCl из экспериментальных данных тоже не такая уж и сложная процедура. Но проблема заключается только в том, что подобный эксперимент — штука сложная. Поэтому проще воспользоваться базой данных, где уже приведены нужные расстояния.

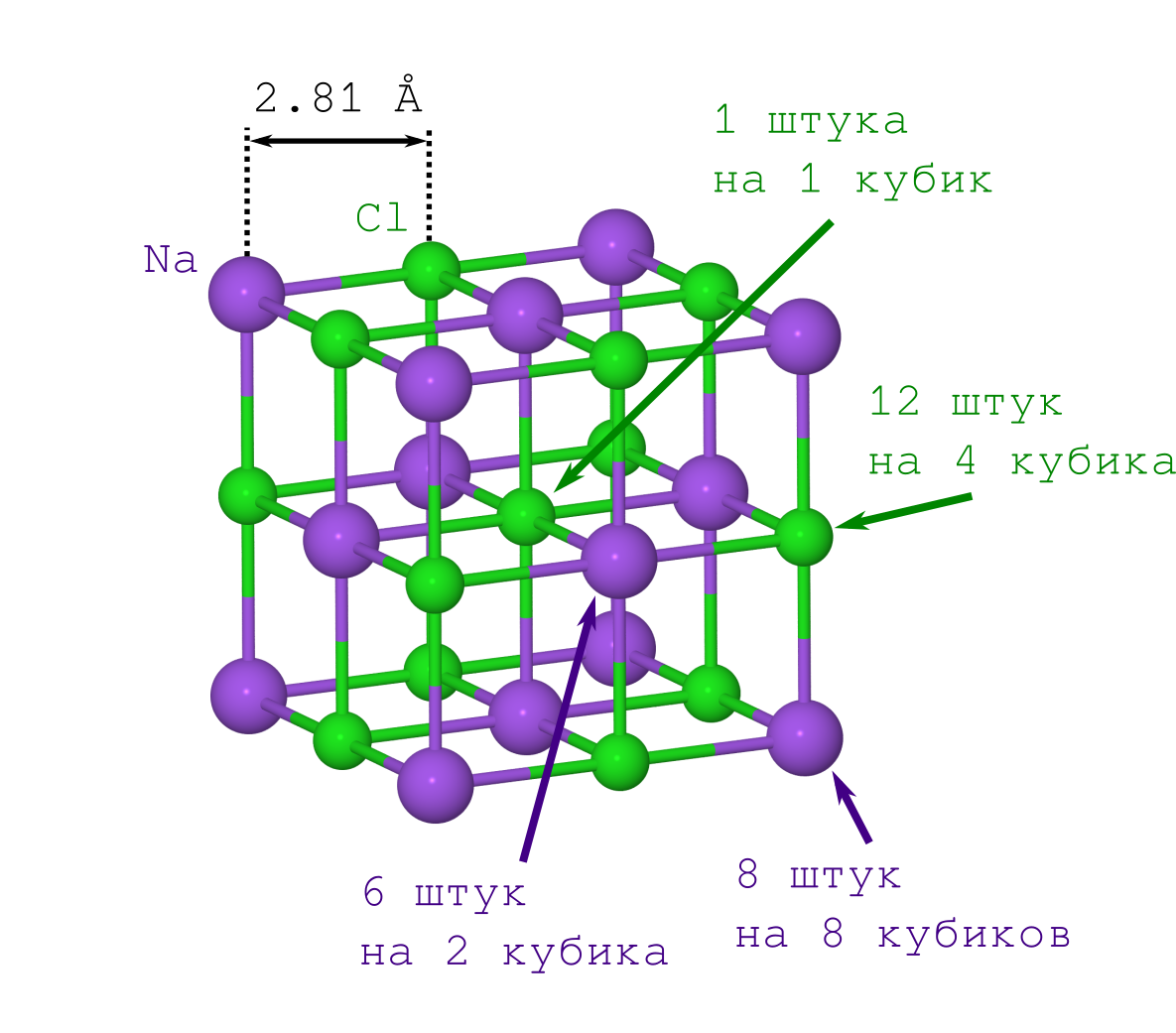
Но для получения расстояния между атомами в кристалле достаточно только плотности кристаллика поваренной соли ρ=2.165 г/см³, которую можно как легко достать из Википедии, так и померить самому в домашних условиях.

Для вычисления расстояния нам понадобится:

плотность кристалла NaCl (есть),
знание расположения ионов этого кристалла.

Если бы делали это впервые (скажем, в начале XX века), то пришлось бы помучиться со вторым пунктом. Но современным людям это уже и так известно: решётка NaCl имеет форму кубика, в котором чередуются между собой ионы Na+ и Cl– (см. картинку выше). Размножая указанный фрагмент кристалла («копипастя» указанный кусок и прилаживая его к предыдущей итерации грань к грани), мы получим кристалл NaCl любого желаемого размера и любой желаемой (майнкрафтовой) формы.
А значит плотность этого кубика должна быть такой же, что и у всего кристалла. Учитывая, что плотность это $\rho = \frac{m}{V}$ (т.е. масса на объём), то получается, что зная массу и геометрическое выражение для объёма мы можем посчитать и расстояние между атомами.

Объём кубика очевиден: длина ребра составляет удвоенное расстояние Na--Cl ( $L=2 r_\mathrm{NaCl}$ ), а значит искомый объём равен $V=L^3 = 8 r_\mathrm{NaCl}^3$ .
С массой же не так всё просто. Большинство атомов у нас лежат на вершинах, рёбрах и гранях кубика, а значит одновременно принадлежат нескольким из этих кубиков. Это надо учесть при вычислениях.

Начнём учёт с ионов Na+. Их у нас всего 2 типа (см. рисунок решётки кристалла):

те, что лежат в вершинах куба (их столько же, сколько и вершин куба, т.е. 8, и они одновременно лежат в 8 кубиках, поэтому надо будет делить это число на 8),
те, что лежат на гранях (их 6 штук, и они одновременно принадлежат 2-м кубикам).

В итоге получаем, что в нашем кубе содержатся $8 \cdot \frac{1}{8} + 6 \cdot \frac{1}{2} =4$ иона натрия.

Теперь о Cl–. Их тоже всего 2 типа (см. рисунок решётки кристалла):

те, что лежат на рёбрах куба (их 12 штук, и они находятся в совместном владении у 4-х кубиков),
тот Cl–, что в центре куба, он один и принадлежит только нашему кубику.

Поэтому нашем кубе содержатся $12 \cdot \frac{1}{4} + 1 \cdot \frac{1}{1} =4$ иона хлора.

Состав кристалла, очевидно, соответствует химической формуле NaCl, но масса нашего кубика оказывается равна (не забываем, что массы атомов в таблице Менделеева даются в атомных единицах массы):

$m = 4 \cdot ( \underbrace{M_\mathrm{Na}}_{23 \ \text{а.е.м.}} + \underbrace{M_\mathrm{Cl}}_{35.5 \ \text{а.е.м.}} ) = 234 \ \text{а.е.м.} = 234 \cdot 1.66 \cdot 10^{-24} \ \text{г} = 3.88 \cdot 10^{-22} \ \text{г} \ .$

Теперь же из соотношения $\rho = \frac{m}{V}$ мы можем составить уравнение на длину $r_\mathrm{NaCl}$ :
$r_\mathrm{NaCl}^3 = \left(\frac{m}{8 \rho} \right)$ ,
которое легко решается:
$r_\mathrm{NaCl} = \left( \frac{m}{8 \rho}\right)^{1/3} = \left( \frac{3.88 \cdot 10^{-22} \ [\text{г}]}{8 \cdot 2.17 \ [\text{г}/\text{см}^{3}]}\right)^{1/3} = 2.82\cdot 10^{-8} \ [\text{см}] = 2.82 \ [\text{Å}]$ .
От данных из рентгеновской кристаллографии 2.81 Å (например из Abrahams, S.C.; Bernstein, J.L. Accuracy of an automatic diffractometer. Measurement of the sodium chloride structure factors // Acta Crystallographica (1965) 18, 926–932) мы промазали всего на 0.01 Å, что достаточно круто.

Кто-то может подумать, что разница в 0.45 Å несущественна, но это почти что боровский радиус (0.52 Å), который равен наиболее вероятному расстоянию электрона, и по атомным меркам разница получается огромная.

Почему NaCl в виде 2-х атомной молекулы отличается от кристалла

Тут всё очень просто. Бесконечная решётка кристалла создаёт возможность необратимого «перепрыгивания» для 3s1 электрона натрия на атом хлора, поскольку получившаяся разность зарядов компенсируется взаимодействием с соседями.

В двухатомной молекуле 3s1 электрон натрия тоже хочет перепрыгнуть на атом хлора (ведь у них большая разность электроотрицательностей), но получающаяся разность зарядов тянет электрон обратно на натрий, в результате устанавливается «равновесие» между двумя резонансными структурами:

$\mathrm{Na:Cl \leftrightarrow Na^+ Cl^-}$

с ковалентной связью (слева) и ионной (справа), причём вторая более выражена.
Этот эффект можно измерить, поскольку реальный заряд на атомах будет не $\pm 1$ , как мы привыкли в школе, а нечто меньшее по модулю.

У молекулы NaCl в газовой фазе известны и расстояние между атомами (2.36 Å), и дипольный момент $d = q \cdot r_\mathrm{NaCl} = 9.0 \ [\text{Дебай}]$ , где $q\geq 0$ и есть искомый модуль зарядов атомов (у натрия заряд будет $+q$ , а у хлора $-q$ ). Дебай для нас не очень удобен, поэтому перейдём к единицам «заряд электрона на ангстрем» при помощи множителя 0.21, т.е. $d = 0.21 \cdot 9.0 = 1.9 \ [q_e\cdot \text{Å}]$ , и в результате решения простейшего уравнения получим: $q = \frac{d}{r_\mathrm{NaCl}} = \frac{1.9}{2.36} = 0.8$ . Вот эти «убежавшие» 0.2 заряда электрона и создают разницу между кристаллом NaCl и молекулой NaCl в газовой фазе.

Ферроцен

Стоит перейти от ионных кристаллов к молекулярным, в которых плотно упакованы молекулы, так сравнивать внезапно становится можно, причём без всяких оговорок.

Но о разнице не нужно забывать. И на эту тему имеется даже классический пример: молекула ферроцена.
Это простейшее сэндвичевое соединение. В нём нейтральный атом железа (как котлетка) зажат между двумя пятичленными ароматическими кольцами (булочками).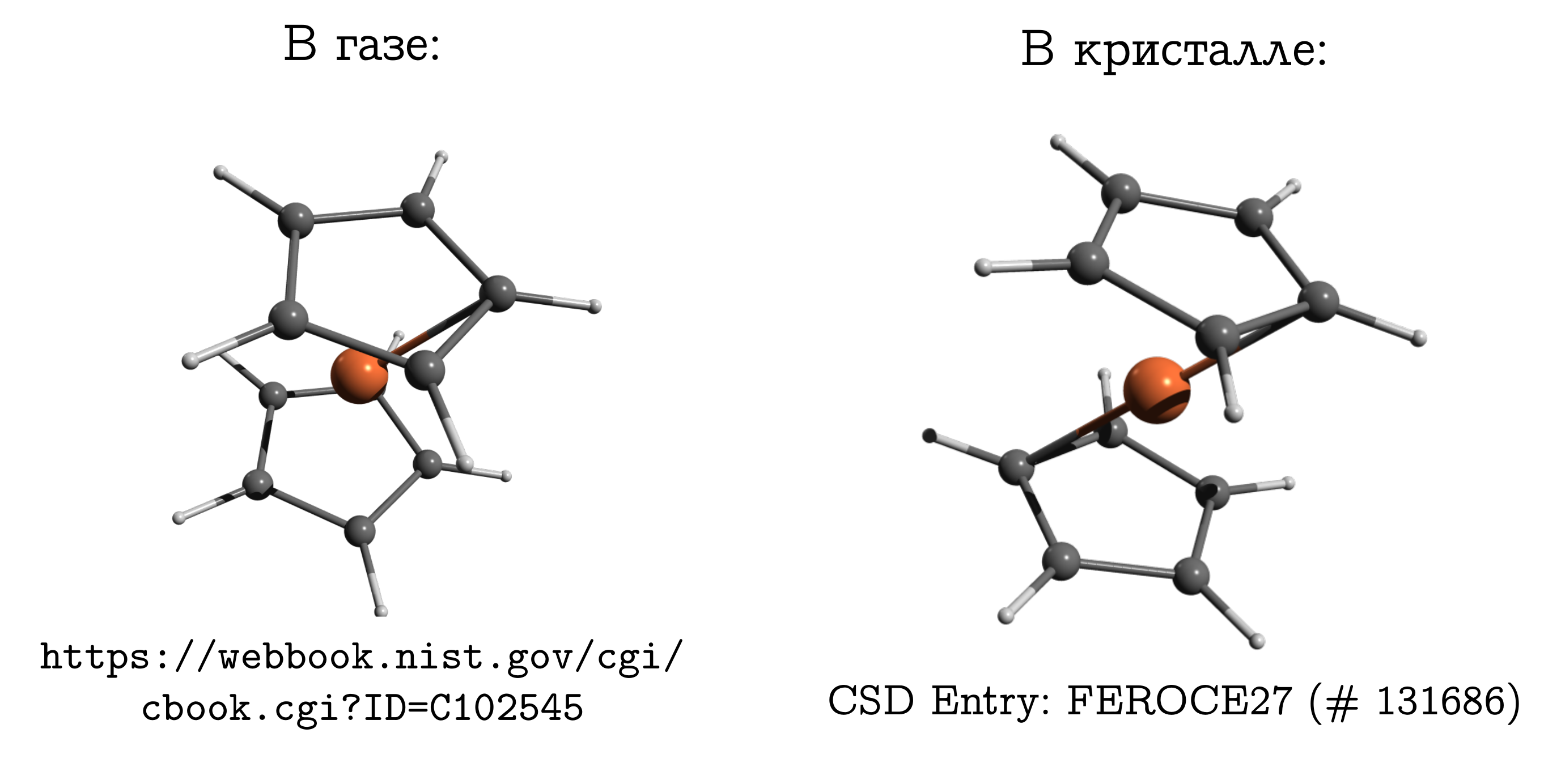

Эту молекулу можно достаточно легко испарить, и узнать, что наиболее стабильной структурой в газовой фазе является т.н. заслонённая конформация. В ней углероды и водороды верхнего и нижнего колец находятся друг напротив друга (см. картинку выше), поскольку в этом случае наиболее сильны дисперсионные взаимодействия между этими кусками молекулы, а дисперсионка — это всегда выгодно.

На самом деле…

Реальность ещё сложнее: в газе эти кольца вращаются друг относительно друга вдоль оси, связывающей центры колец и атом железа, но заслонённая конформация всё равно будет самой выгодной.

Если же мы возьмём кристалл ферроцена, то окажется, что там молекулы имеют другую стабильную конформацию (которую для углеводородов называют заторможенной), в которой водород и углерод одного кольца находятся над/под связью C--C другого. Между молекулами тоже есть дисперсионные взаимодействия, и подобная, вроде неудобная для молекулы, структура возникает из-за того, что молекулам проще уложиться близко друг другу только в неудобной для себя форме, а это личное неудобство компенсировать взаимодействием друг с другом.

Почему ферроцен так сильно отличается от этана

Человеку, знакомому с химией, обычно приходится пересиливать себя, чтобы запомнить структуру ферроцена в газе. Ведь у него есть воспоминания о этане (С2H6), у которого наиболее стабильной конформацией является заторможенная (когда водороды одного куска CH3 лежат «между» водородами другого CH3), т.к. в этом положении минимизируется межатомное отталкивание между электронными оболочками водородов.

Взято из www.chem.msu.su/rus/teaching/stereo

А здесь вся разница в расстоянии. Стандартной формой потенциала дисперсионных взаимодействий является потенциал Леннарда-Джонса (это, кстати, один, а не два мужика):

$V_\mathrm{LJ}(r) = \frac{A}{r^{12}} - \frac{B}{r^{6}}$

В нём первое слагаемое берётся из межатомного отталкивания, а второе — из межатомного притяжения, возникающего из флуктуаций электронной плотности. В целом, этот потенциал выглядит как-то так:

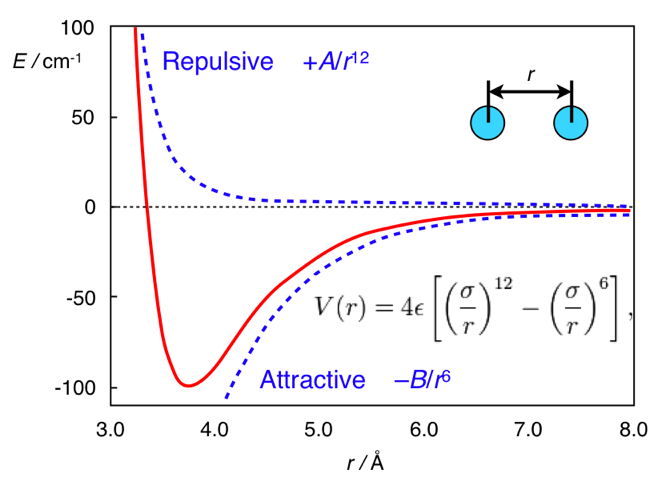
Потенциал Леннарда-Джонса. Взято из chemistry.stackexchange.com/questions/34214/physical-significance-of-double-well-potential-in-quantum-bonding

И в случае этана, атомы водорода находятся слишком близко друг к другу, поэтому они находятся (относительно её минимума) в левой части кривой, и для них характерно отталкивание. В случае же ферроцена, между кольцами есть прослойка нехилого размера (атом железа), из-за которого кольца оказываются достаточно далеко, чтобы не чувствовать межатомное отталкивание. И поэтому они находятся на правой (притягивающей) части потенциала.

Гистамин

В случае ферроцена мы увидели т.н. конформационные различия: молекула осталась одной и той же (т.е. никаких химических связей не порвалось и не образовалось), а её форма чуть-чуть изменилась.
Но отличия могут быть ещё более сильными, например, если в системе у нас возможны т.н. таутомерные превращения. Таутомеризация — это класс химических реакций, которые происходят так легко и быстро, что в итоге у нас могут одновременно существовать несколько изомеров одной молекулы, легко переходящие друг в друга. Эти изомеры называют таутомерами.
Стандартный пример подобного: кето-енольная таутомерия в кетонах:

Чаще всего, как и в этом примере, таутомерия связана с перескоком протона с одного тёпленького места на другое. И завязаны эти реакции на туннельный эффект, которому водород, как самый легкий из атомов, наиболее подвержен.
Подобные химические превращения характерны для многих биологических молекул, например для азотистых оснований, входящих в состав ДНК, или для сахаров.
Но вот при переходе от системы к системе часто меняются константы равновесия подобных реакций, поэтому в разных фазах мы можем наблюдать разный таутомерный состав.

Примером этого можно взять молекулу гистамина (см. рис. ниже).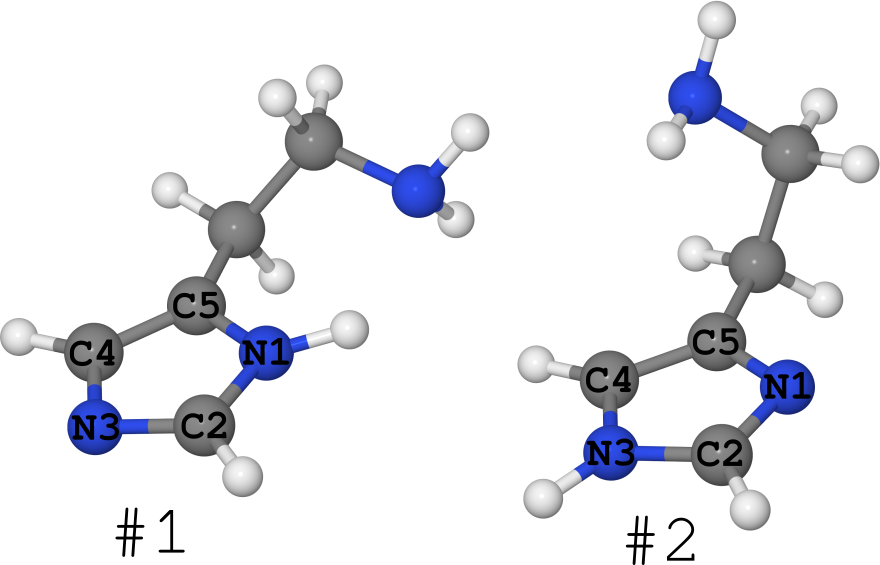

Она существует в виде 2-х таутомеров (про количество конформеров я вообще молчу, их очень много):

#1, где водород сидит на азоте N1,
#2, где водород сидит на азоте N3.

Так получилось, что для этой молекулы известна её структуры в разных фазах.

В кристалле она находится полностью «замороженной» в форме #1. (см. статью DOI: 10.1021/ja00796a011 и структуру в кембриджском банке структур под именем «HISTAN» и/или номером 1176642)
В водных растворах эта молекула существует в обеих формах, причём таутомера #2 заметно больше (DOI: 10.1021/ja027103x).
В газе же гистамин существует в равной степени в форме #1 и в форме #2 (DOI: 10.1021/ja980560m).

Т.е. разные фазы содержат разное количество разных молекул, а значит они — разные системы.

Вывод об Ошибке #1

Главный вывод, который нужно сделать из приведённых примеров таков:

При сравнении расчётов в одной фазе с экспериментом в другой надо быть готовым к систематическим отличиям.

Это не означает, что не надо сравнивать: сравнивать надо, но просто надо критичнее относиться к обнаруженным различиям и/или совпадениям, и по возможности оценивать подобные эффекты.

Ошибка #2. «Зоопарк» молекулярных параметров.

Вторая ошибка вкратце описывается так: если параметры называются похоже, но не одинаково — это разные параметры.
Чтобы понять, в чём же заключается источник подобного несогласия теории и эксперимента, придётся поподробнее разобрать и те стандартные экспериментальные методы, которые используются для получения молекулярных параметров, и модели, которыми аналогичные величины обсчитывают чисто из теории.
И здесь мы вновь будем говорить только о структурах.

Как получают экспериментальные структуры молекул

Чтобы как-то ограничить себя, поговорим только о методах исследования структуры одиночных молекул, т.е. о газовой фазе.
Основных источников подобной информации у нас два:

газовая электронография,
микроволновая спектроскопия.

На каждом из этих методов остановимся чуть поподробнее.

Газовая электронография

Метод достаточно старый, своё начало он берет в 30-х годах XX века, когда немецкие учёные Марк и Вирль провели первые эксперименты по дифракции электронов на газе.
Мало кто знает, но этот метод исследования причастен к получению трёх нобелевских премий по химии.

3 нобеля с электронографическим вкладом

Питер Дебай в 1936-м году получил свою награду с формулировкой:

»[for his work on] molecular structure through his investigations on dipole moments and the diffraction of X-rays and electrons in gases»

Это единственное явное упоминание газовой электронографии в заслугах лауреата, и не спроста. Основное уравнение электронографии для интенсивности молекулярного рассеяния носит имя Дебая.
собственно, уравнение Дебая

И несмотря на то, что об этом замечательном физике помнят что угодно (модель ионных растворов, его модель для расчёта теплоёмкости кристаллов), но только не электронографию, главный научный приз он получил (в частности) за неё.
Лайнус Полинг в 1954. Да, тот самый, получивший 2 личные нобелевские премии, да ещё и посадивший весь мир на витамин C, Великий Полинг. В бытность своей работы в Калтехе он, в частности, занимался газовой электронографией (см., например, DOI: 10.1021/ja01873a047). И конечно, знание структурной химии свободных молекул помогло ему создать знаменитую теорию химической связи (но не будем тут принижать и его большой кристаллографический бэкграунд).
Одд Хассель, лауреат 1969 года. Свою ½ нобелевской премии он получил за открытие конформационного равновесия. Сделал он это на основе электронографического исследования циклогексана. Эта молекула существует в виде двух конформаций: кресло (chair) и ванная (в английской традиции — лодка, boat).

Отсюда: www.shapeways.com/product/N5FE298DS/cyclohexane-2-molecules-boat-and-chair-form
Эти варианты расположения атомов быстро переходят друг в дружку, но в то время об этом не знали, и считали, что должна реализовываться только одна из структур. Только вот электронографический сигнал никак не хотел описываться ни одной из этих структур, и только комбинация сигналов от обеих конформаций смогла объяснить наблюдающуюся дифракционную картину (об этом можно подробнее почитать в книге И. Харгиттаи «Откровенная наука. Беседы со знаменитыми химиками»).

Схема самого метода очень проста (см. картинку ниже).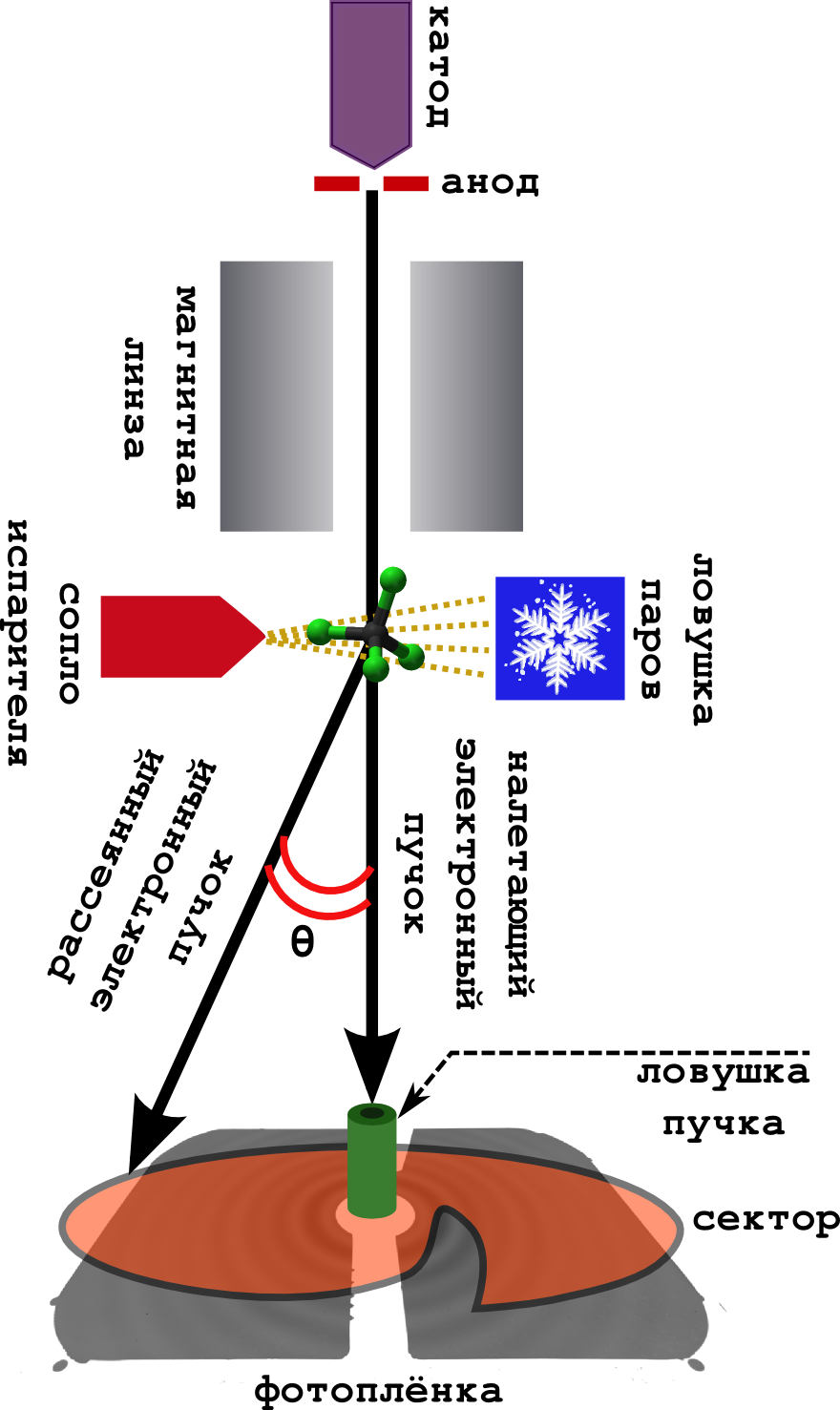

Дело происходит в вакууме.

С катода непрерывно выбиваются быстрые электроны, которые ускоряются в поле анода до энергий 40–60 кэВ.
Достаточно разбросанные (но быстрые) электроны фокусируются магнитной линзой, после чего они превращаются в узкий пучок.
Перпендикулярно пучку установлена камера с веществом. Образец нагревается до кипения, и получившийся пар выходит на встречу электронному пучку.
Электроны успешно рассеиваются на молекулах, и спокойно улетают дальше, где попадают на фотоплёнку.
Обычно перед фотоплёкой ставят т.н. секторное устройство. Это очень быстро вращающаяся ширма необычной формы. Дело в том, что у электрона вероятность отклониться от изначального направления (на большой углол рассеяния $\theta$ ), очень быстро падает. Поэтому, чтобы сгладить это падение интенсивности, сектор равномерно затмевает центральную часть фотоплёнки, оставляя дальнюю часть открытой. В результате получается более равномерно засвеченная картина.
Ловушка пучка ловит те электроны, что не рассеялись совсем (а их очень много).
Ну, и чтобы молекулы не летали по всему прибору, пачкая его, их вымораживают на холодной ловушке, охлаждаемой жидким азотом.

В итоге получается та самая дифракционная картина из концентрических колец, описываемая уравнением Дебая (это сигнал). Из неё можно потом вытащить напрямую различные молекулярные параметры.

Где можно найти лаборатории, занимающиеся газовой электронографией?

Их не так уж и много осталось.
Но в РФ их две: Москве (на Химфаке МГУ), и в Ивановском Химико-Технологическом Университете.

Микроволновая спектроскопия

Этот метод исследования молекул известен больше, поэтому о нём я поговорю чуть более кратко, на примере наиболее современной модификации: спектрометра с Фурье преобразованием (хз как по-русски, короче Fourier-transformed microwave spectroscopy).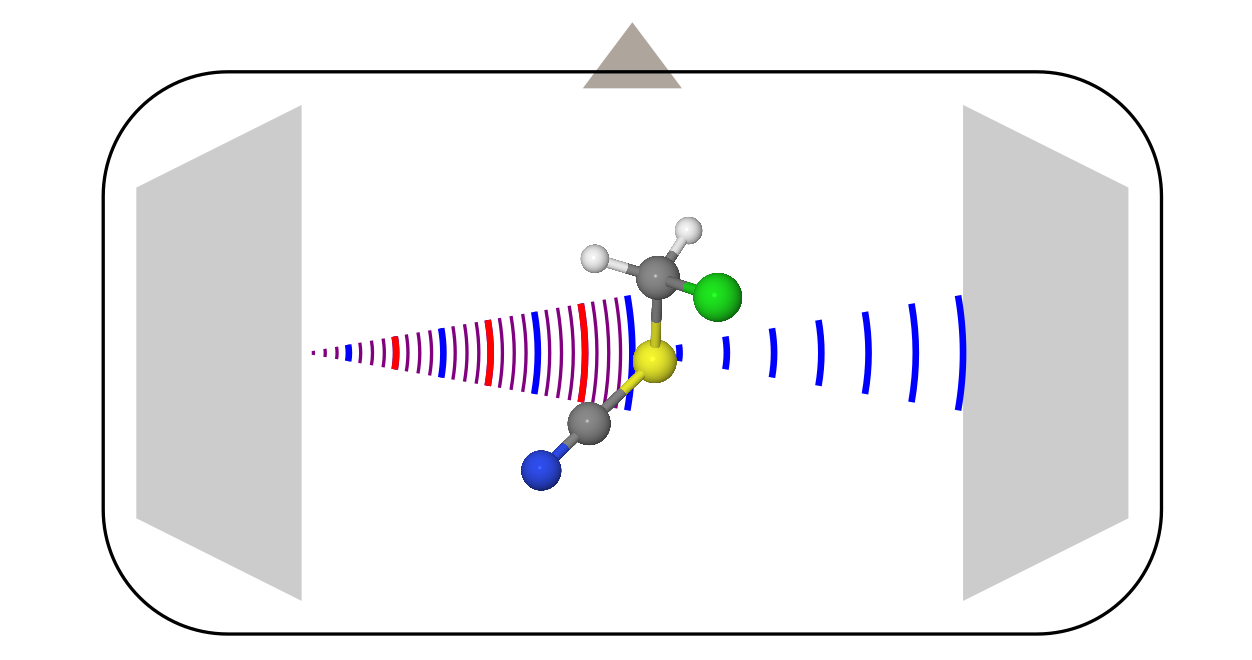

Конструкция тут уже более сложная, поскольку она требует кучу разной электроники (усилители, частотные модуляторы и т.д.). Всё это мы опустим, и поговорим только о том, что происходит внутри вакуумной камеры.

Друг напротив друга стоят две рупорные антенны (наподобие той, которой открыли реликтовое изучение). Одна из них служит в качестве передатчика, а вторая является приёмником.
Перпендикулярно этим антеннам стоит клапан, который запускает образец. Чаще всего он запускается в виде пара вместе с неким газом носителем (обычно это инертные газы) в режиме адиабатического расширения. В таких условиях молекулы быстро охлаждаются до температур около 0 К, что существенно упрощает спектр, делая его более податливым к интерпретации.
Когда молекулы заполняют всю камеру, передающая антенна облучает их сигналом с линейной частотной модуляцией. В частотном представлении это соответствует сумме всех частот в некотором диапазоне.
Некоторые молекулы поглощают это излучение на разных переданных частотах, и переходят в возбуждённое состояние. Но, через некоторое время они сваливаются обратно, начиная излучать то, что они нахапали при импульсе от передающей антенны. Это сваливание выглядит как убывающий осциллирующий сигнал (free induction decay). Вторая антенна его и регистрирует. Потом, после Фурье-преобразования записи этого сигнала во времени, получается обычный спектр от частоты.

В отличие от электронографии, которой было не важно, что за молекулы рассматривать, в микроволновой спектроскопии молекула должна обладать постоянным дипольным моментом (в редких случаях подходит и магнитно-дипольный момент, это характерно для радикалов, типа молекулы O2). Сигналом же тут является «интенсивность испускания vs. частота». Из этих спектров через некоторые модели извлекают вращательные постоянные, из которых уже потом достают структуру молекул.

Добро пожаловать в Зоопарк Молекулярных Параметров!

Теперь пришло время посмотреть на то, какие геометрические параметры мы можем вытащить из различных экспериментах. По-сути, каждый из типов величин обозначает что за модель была использована для подгонки экспериментального сигнала (чаще всего по методу наименьших квадратов). Большинство из приведённых параметров можно отыскать в обзоре Kuchitsu K., Cyvin S.J. // In: Molecular Structure and Vibrations / Cyvin S