Шифрование TEA, XTEA, XXTEA22.12.2020 20:18

Содержание статьи

Описание алгоритма шифрования TEA
Реализация TEA
Устраняем критические ошибки TEA и получаем XTEA (Block TEA)
Реализация XTEA
Еще лучше: XXTEA (Corrected Block TEA)
Криптоанализ алгоритмов шифрования

Введение

Рассмотрим некоторые определения, используемые в статье. Существуют два типа шифрования: симметричные и несимметричные.

В симметричных алгоритмах шифрования один и тот же ключ используется и для шифрования данных, и для их расшифровки. Этот ключ должны знать знать только отправитель и получатель, иначе данные в руках злоумышленников по сути не являются зашифрованными. Человек, зная ключ, который не должен знать, может расшифровать шифротекст и узнать, что вы попросили друга купить в магазине макароны.

В несимметричных алгоритмах шифрования уже используется не один ключ, а целых два: открытый и закрытый. Шифруются данные открытым ключом, расшифровываются только закрытым. Открытый ключ можно раздать всем желающим, а закрытый ключ требуется держать в тайне.

TEA, XTEA, XXTEA являются блочными алгоритмами шифрования. Это вид симметричного шифрования, который оперирует группами бит, фиксированной длины, которые называются блоками.

В данной статье рассматриваются блочные симметричные алгоритмы шифрования, которые в качестве фундамента используют сеть Фейстеля, как и большинство современных блочных шифров.

Ознакомиться с сетью Фейстеля подробнее можете в данной статье.

TEA

TEA a.k.a. Tiny Encryption Algorithm — блочный симметричный алгоритм шифрования. Достаточно скромный и не требуют большой памяти, быстр в выполнении и прост в реализации, благодаря чему нашел широкое применение в криптографии.

Перейдем к самому алгоритму. Данные делятся на блоки по 64 бит, а ключ на четыре части по 32 бита: . Если данные в битовом представлении не делятся на 64, то дополняем ее нулевыми битами. Далее происходит шифрование: целый 32 цикла по 2 раунда. Раунд — это один шаг цикла. То есть множество циклов еще разбивается на части. Для математического описания алгоритма введем операции:

$\delta = \left(\sqrt{5} - 1\right) \cdot 2^{31}$ -- чиселка, которая нужна для противостояния простым атакам. Можно было взять любую константу, автор шифра решил воспользоваться золотым сечением

$X \ll Y$ -- побитовый сдвиг числа X на Y бит влево (вправо аналогично)

$X \oplus Y$ -- побитовое исключающее ИЛИ — XOR

$X \boxplus Y$ -- сложение чисел по модулю $2^{32}$

На n-ом раунде на вход поступает блок, состоящий из двух частей: правой и левой $\left( L_n, R_n \right)$ , выходит тоже блок из двух частей $\left( L_{n+1}, R_{n+1} \right)$ по правилам:

Просто перебрасываем: $L_{n+1} = R_n$

Четный раунд:

Нечетный:

Заметим, что меняется только используемый ключ. Для наглядности приведем блок схема алгоритма:

Блок-схема TEA

Реализация TEA

Приведем код, в котором реализован TEA на языке программирования С. Авторами данного кода являются создатели самого шифра: David J. Wheeler и Roger M. Needham. Первоисточник — их статья.

k[0], k[1], k[2], k[3] — ключ, разбитый на четыре части
v[0], v[1] — данные, которые хотим зашифровать
encode — (true), когда хотим зашифровать данные, (false), когда хотим расшифровать

void tea(long* v, long* k, bool encode) {
  unsigned long y = v[0];
  unsigned long z = v[1];
  unsigned long sum = 0;
  unsigned long delta = 0x9e3779b9;
  unsigned long n = 32;
  
  if(encode) {
    
    // encoding
  
    while(n-- > 0) {
      sum += delta;
      y += ((z << 4) + k[0]) ^ (z + sum) ^ ((z >> 5) + k[1]);
      z += ((y << 4) + k[2]) ^ (y + sum) ^ ((y >> 5) + k[3]);
    }
  
  } else {
    
    // decoding
  
    sum = delta << 5;
  
    while(n-- > 0) {
      z -= ((y << 4) + k[2]) ^ (y + sum) ^ ((y >> 5) + k[3]);
      y -= ((z << 4) + k[0]) ^ (z + sum) ^ ((z >> 5) + k[1]);
      sum -= delta;
    }
  }
  
  v[0] = y;
  v[1] = z;
  
  return;
}

XTEA

В TEA со временем нашли серьезные уязвимости, что натолкнуло на его улучшение, что в последствии привело к созданию нового алгоритма XTEA.

XTEA a.k.a. eXtended TEA — алгоритм шифрования, в котором устранены критические ошибки TEA. Предоставлен теми же David J. Wheeler и Roger M. Needham. Как и TEA, оперирует блоками по 64 бита. Единственная разница в том, что в TEA ключ в каждом цикле выбирался одинаково, не было никакого разнообразия. В XTEA эту предсказуемость шифра убрали. Теперь выбор одного из четырех частей ключа выполняется с использованием золотого сечения (в конце математических операций просто берется остаток от деления на 4).

Перейдем к математике. На n-ом раунде $n \in [1; 64]$ снова на ход поступают данные, разделенные пополам: $\left( L_n, R_n \right)$ , выходят $\left( L_{n+1}, R_{n+1} \right)$ по правилам:

Снова просто перебрасываем: $L_{n+1} = R_n$

Четный раунд:

Нечетный:

Блок схема:

Блок-схема XTEA

Реализация XTEA

Снова приведем код, в котором создатели шифра David J. Wheeler и Roger M. Needham реализовали свой алгоритм на языке программирования С. То, как выглядит оригинальный код (он фактически ничем не отличается), можете посмотреть в их публикации.

v — исходные данные из 2 частей
k — ключ из 4 частей
N — число циклов (создатель шифра рекомендует 32)
long — 32 бита

void xtea(long* v, long* k, long N) {
  unsigned long y = v[0];
  unsigned long z = v[1];
  unsigned long delta = 0x9e3779b9;
  
  if(N > 0) {
    
    // encoding
    
    unsigned long limit = delta * N;
    unsigned long sum = 0;
    
    while(sum != limit) {
      y += (z << 4 ^ z >> 5) + z ^ sum + k[sum & 3];
      sum += delta;
      z += (y << 4 ^ y >> 5) + y ^ sum + k[sum >> 11 & 3];
    }
    
  } else {
    
    // decoding
    
    unsigned long sum = delta * (-N);
    
    while (sum) {
      z -= (y << 4 ^ y >> 5) + y ^ sum + k[sum >> 11 & 3];
      sum -= delta;
      y -= (z << 4 ^ z >> 5) + z ^ sum + k[sum & 3];
    }
    
  }
  
  v[0] = y;
  v[1] = z;
  
  return;
}

Обнаруженные у XTEA уязвимости привели к ряду улучшений: XTEA-1, XTEA-2, XTEA-3. Однако они не получили столь широкого применения на практике. Данные алгоритмы в статье рассматриваться не будут.

XXTEA

XXTEA a.k.a. Corrected Block TEA (т.к. XTEA называют еще Block TEA) — как понятно из названия, улучшенная версия XTEA. Авторами, снова являются David J. Wheeler и Roger M. Needham, которые просто улучшили свой старый алгоритм. Они утверждают, что для простоты использования и общей безопасности предпочтительнее использовать версию с большими блоками, если это применимо, по следующим причинам:

Изменение одного бита изменит примерно половину битов всего блока, не оставив следа
Даже если используется правильное использование постоянного изменения отправляемых данных (возможно, по номеру сообщения), только идентичные сообщения дают одинаковый результат, а утечка информации минимальна
Номер сообщения всегда следует проверять, поскольку эта избыточность является проверкой случайного принимаемого сообщения
Атака «человек посередине», судя по всему, невозможна
Если недопустимо иметь очень длинные сообщения, их можно разбить на блоки, скажем по 60 слов, и связать их аналогично методам, используемым для DES

Как уже описывалось выше, в XXTEA данные шифруются примерно таким же образом. Снова делим данные на блоки, которые еще поделим пополам, ключ, как и в предыдущих случаях, разбивается на четыре части. За один раунд зашифровывается одно слово из блока. Рассмотрим шифрование одного слова на n-ом раунде:

Пусть слово состоит из правого и левого частей. Константа $\delta$ такая же, как во все прошлые разы. Выберем сначала ключ (один из четырех): $K_{\left[ \left( \delta \cdot n \gg 2 \right) \oplus n \right] ~ \text{mod} ~ 4}$ . Рассчитаем два параметра:

$\alpha = \left( L \ll 2 ~ \oplus ~ R \gg 5 \right) \boxplus \left( L \gg 3 ~ \oplus ~ R \ll 4 \right)$
$\beta = \left( \delta \cdot n ~ \oplus ~ L \right) \boxplus \left( K_{\left[ \left( \delta \cdot n \gg 2 \right) \oplus n \right] ~ \text{mod} ~ 4} ~ \oplus ~ R \right)$

Тогда зашифрованное слово получится: $\left( \alpha ~ \oplus ~ \beta \right) \boxplus \left( LR \right), ~~~ LR - \text{слово целиком}$

Приведем блок-схему:

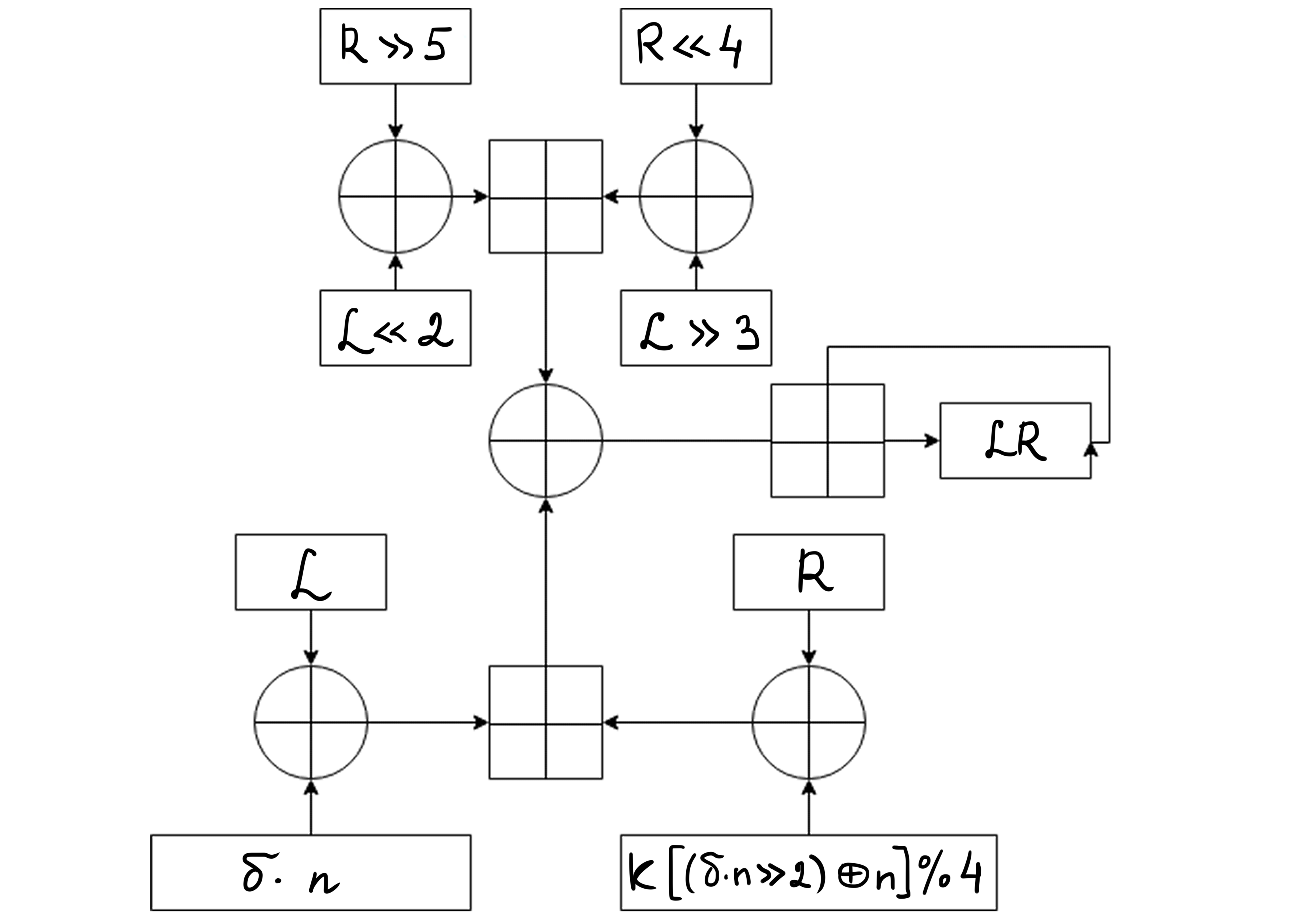Блок-схема XXTEA

Реализация XXTEA

Приведем код, предложенный самими авторами алгоритма шифрования — David J. Wheeler и Roger M. Needham. Подробнее в их статье.

v — слово из 2 частей
k — ключ из 4 частей
N — число циклов
long — 32 бита

#define MX (z >> 5 ^ y << 2) + (y >> 3 ^ z << 4) ^ (sum ^ y) + (k[p & 3 ^ e] ^ z)

long xxtea(long* v, long * k, long N) {
  unsigned long z = v[N - 1];
  unsigned long y = v[0];
  unsigned long sum = 0;
  unsigned long e = 0;
  unsigned long delta = 0x9e3779b9;
  
  long m = 0;
  long p = 0;
  long q = 0;
  
  if(N > 1) {
    
    // encoding
    
    q = 6 + 52 / N;
    
    while(q-- > 0) {
      sum += delta;
      e = sum >> 2 & 3;
      for(p = 0; p < N - 1; p++) {
        y = v[p + 1];
        z = v[p] += MX;
      }
      y = v[0];
      z = v[N - 1] += MX;
    }
    
    return 0;
  } else if(N < -1) {
    
    // decoding
    
    N = -N;
    q = 6 + 52 / N;
    sum = q * delta;
    
    while(sum != 0) {
      e = sum >> 2 & 3;
      for(p = N - 1; p > 0; p--) {
        z = v[p - 1];
        y = v[p] -= MX;
      }
      z = v[N - 1];
      y = v[0] -= MX;
    }
    
    return 0;
  }
  
  return 1;
}

Анализ TEA, XTEA, XXTEA

TEA не особо подвержен атакам дифференциального криптоанализа. Для 17 раундов получается сложность по времени порядка $2^{123}$ . Однако при «атаке на связанных ключах» TEA уязвим, так как ключи распределены внутри цикла статически (всегда один и тот же выбор). Еще возникает проблема с эквивалентными ключами: на каждый ключ есть три эквивалентных, которые зашифровывают и расшифровывают данные таким же образом.

XTEA, как ни странно, является более защищенным, чем TEA. Но из-за особенностей реализации (присутствие XOR) XTEA хуже справляется с дифференциальными и усеченными дифференциальными атаками, чем TEA. Лучший способ расправиться с XTEA шифрованием — дифференциальная атака на связанных ключах.

XXTEA уже неплох. E. Yarrkov в 2010 году реализует атаку на основе подобранного открытого текста против всего цикла XXTEA с широким блоком. Работа основана на дифференциальном криптоанализе. Чтобы зашифровать 212 байт и более, алгоритм выполняет всего 6 раундов, а тщательно подобранные битовые комбинации позволяют обнаруживать и анализировать лавинный эффект. Но E. Yarrkov говорит, что добавление двух дополнительных раундов устраняет эту проблему.