Серебряная пуля для кремлевского демона27.02.2021 10:32

image
Вот, наконец, в теме помех навигации мы и добрались до самого крутого и интересного. Причем, это интересное оказалось не таким уж сложным технически.

Это интересное — пространственная обработка сигналов с антенных решеток. В обычной, особенно любительской, практике радиосвязи и радионавигации такое все еще редко встречается. Виной тому дополнительные кратные затраты на количество радио-трактов. Но иногда это вполне допустимо. Например, в мобильной связи. Здесь широко применяется пространственная обработка, MIMO. Даже в обычной точке доступа WiFi она уже есть давно.

Хотя в любительской радиотехнике все еще мало примеров использования пространственной обработки, она начинает завоевывать свое место. Этому способствует снижение цен на платы SDR с 2×2 MIMO, такие как LimeSDR или XTRX. Существуют даже относительно недорогие решения и для Massive MIMO.

В практике спутниковой радионавигации антенные решетки встречаются еще реже. Наверное, это происходит из-за узости области знаний, но не только. Немаловажным фактором остается сложность схем обработки. Сигналы спутников GPS, ГЛОНАСС и других имеют на поверхности Земли столь малую мощность, что даже неискушенный нарушитель легко создает помеху, в миллионы раз превышающую эту мощность. Что уж говорить про государственных нарушителей, за которыми мне пришлось гоняться несколько лет назад. Вся Москва не даст соврать. Кремлевские демоны!

Проблема общенародная, поэтому срочно переходим к практике. Берем четырехканальную антенную решетку диапазона L1. Берем четырехканальную SDR-плату для спутниковой навигации. Соединяем.

image

Делаем синхронную запись сигнала с четырех антенн с подоконника. При этом с выхода LimeSDR излучаем гармоническую помеху на центральной частоте GPS L1 — 1575.42МГц. Спектр сигнала получается такой:

image

Для построения спектра мы используем программу на Matlab, полученную от prof. Dennis Akos и слегка модифицированную для работы с 16-битным комплексным сигналом. Здесь лежит архив с исходниками.

Кроме спектра, программа выводит более подробные параметры сигнала: гистограмма и график во времени.

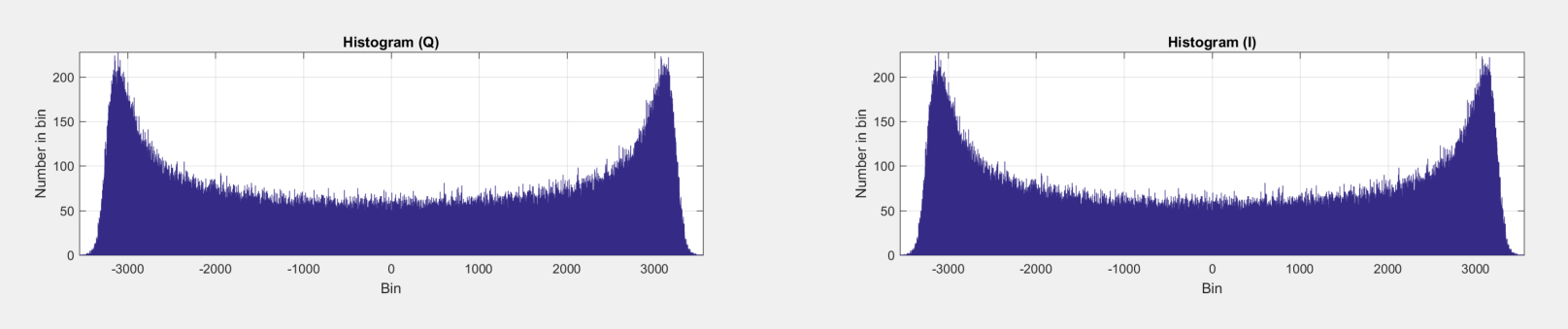
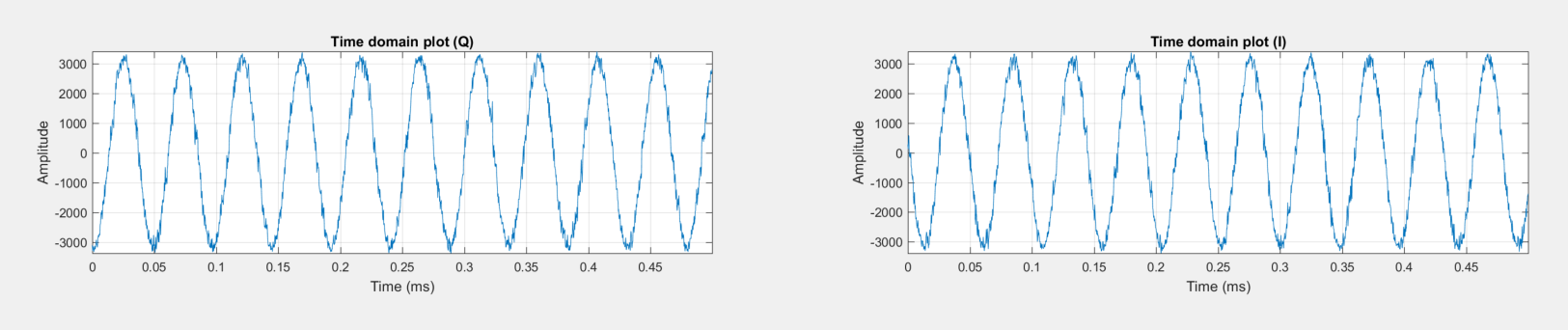
image
image

Анализ графиков показывает, что входной сигнал заполняет практически весь доступный динамический диапазон цифрового тракта. От максимума сигнала до шума примерно 60 дБ, что, даже с учетом усиления от обработки БПФ, довольно много. Проверим, что этого достаточно, чтобы сигналы спутников не находились коррелятором.

image

Как видно, «спектр» сигналов GPS L1 C/A-code равномерный, без всплесков. Это значит, что сигналы спутников не обнаружены. Проверяем так четыре файла (с каждой антенны) — ничего.

Теперь ударим легкой математикой по радио-электронной преступности. Возьмем такой простой код на Matlab: 

% clean up
clear;
close all;
clc;

% read data from 4 files
fileNames = ['c:\work\aj\habr1\dump2\Dump_15_channel_0.int16';...
             'c:\work\aj\habr1\dump2\Dump_15_channel_1.int16';...
             'c:\work\aj\habr1\dump2\Dump_15_channel_2.int16';...
             'c:\work\aj\habr1\dump2\Dump_15_channel_3.int16'];

countFiles = size(fileNames,1);
countInSamples = 5000000;
dataArr = zeros(countFiles, countInSamples);
fID = 0;
for i = 1:countFiles
    fID = fopen(fileNames(i,:));
    if (fID == -1)
        fprintf('This file does not exist: %s\n', fileNames(i,:));
        return;
    else
        data = fread(fID, countInSamples, 'int16');
        dataArr(i,:) = data;
        fclose(fID);
    end
end

countInSamples

% create I/Q array
dataArrIQ = zeros(countFiles, countInSamples/2);
for i = 1:countFiles
    k = 1;
    for j = 1:2:countInSamples
        dataArrIQ(i, k) = complex(dataArr(i, j), dataArr(i, j + 1));
        k = k + 1;
    end
end

20*log10(mean(abs(dataArrIQ),2))

res = (diag(diag(inv(corrcoef(dataArrIQ'))).^(-1)) / corrcoef(dataArrIQ')) * dataArrIQ;

20*log10(mean(abs(res),2))

% write the result into 4 files
for i = 1:countFiles
    out = zeros(1, countInSamples);
    for j = 1:(countInSamples/2)
        out(2*j-1) = real(res(i,j));
        out(2*j) = imag(res(i,j));
    end
    fID = fopen(strcat('out',num2str(i),'.int16'),'w');
    fwrite(fID, out, 'int16');
    fclose(fID);
end

Здесь специально приведен код со всеми потрохами, чтобы вы могли скопировать его и использовать для запусков и улучшений. После запуска этого простейшего пространственного компенсатора помех получаются выходные файлы, из которых мы выбираем лучший и опять проверяем на программном приемнике профессора Акоса.

image

По спектру мы видим, что помеха не пропала совсем, но уменьшилась по уровню примерно на 30 дБ. Почему же она не упала ниже? Следующий график даёт нам разгадку.

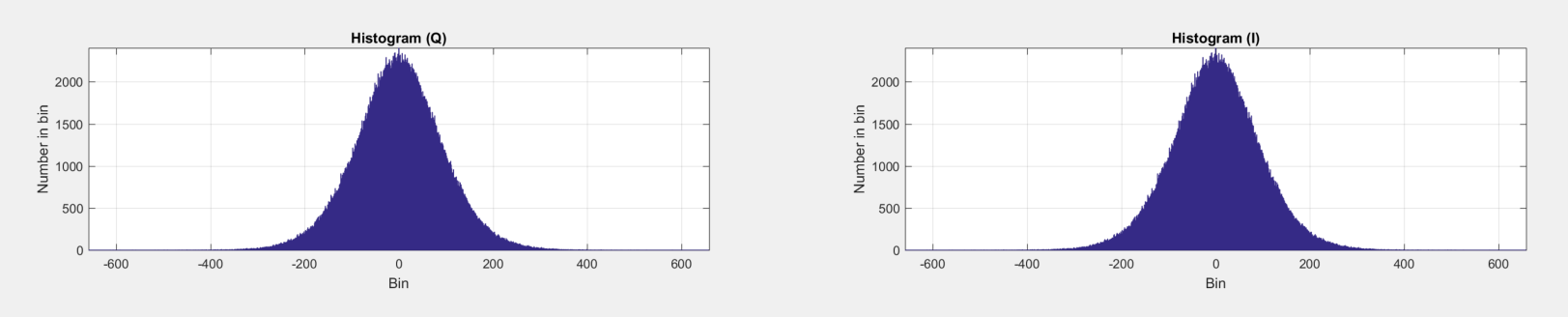
image

Статистика отсчетов на выходе компенсатора похожа на статистику шума. График спектра получен с помощью преобразования Фурье, которое «обнажает» гармонические составляющие смеси помехи и шума. А в широкой полосе маленькие остатки помех «тонут» в шуме. Ниже шума подавить помеху у нас не получилось. Физика. Хотя во временной области гармоника остается видимой.

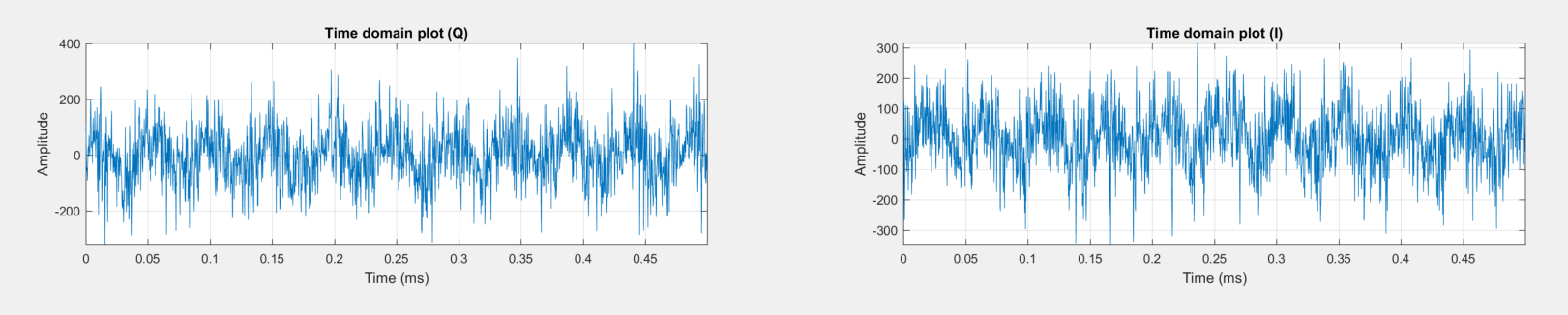
image

Итак, помеха уменьшилась на 30 дБ. Что же теперь покажет нам коррелятор? Сможет ли он найти сигнал?

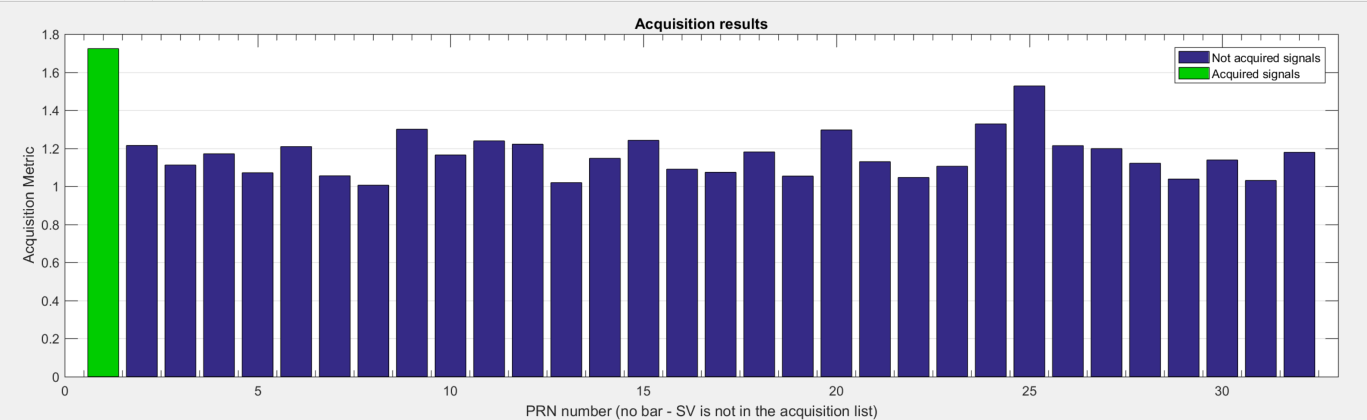
image

Вуаля! Сигнал найден! Приемник обнаружил спутник в номером 1. Уровень корреляции не очень, но давайте дадим приемнику немного поработать и посмотрим на результаты.

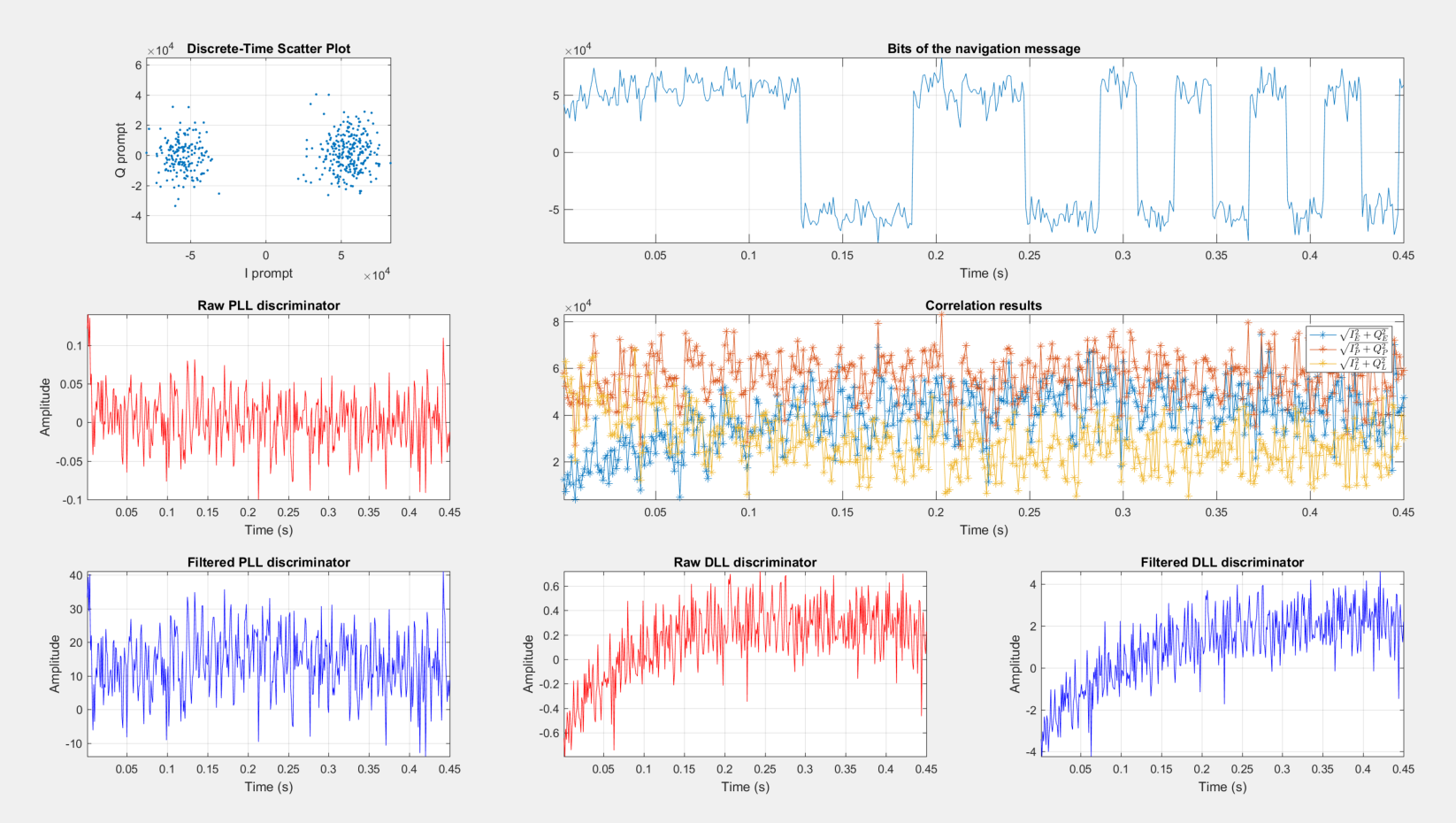
image

На верхних графиках мы можем довольно четко видеть сигнальное созвездие и результат демодуляции. Результаты работы коррелятора, петли по фазе и по задержке выглядят не очень. Они со временем загибаются. Это можно объяснить недостатками представленного алгоритма компенсатора, о которых мы поговорим позже. Но это не меняет главного: помеха удалена силой математики!

Благодаря Матлабу вся математика заключена в одной строчке кода: 

res = (diag(diag(inv(corrcoef(dataArrIQ'))).^(-1)) / corrcoef(dataArrIQ')) * dataArrIQ;

В более читаемом виде код будет таким: 

cm = corrcoef(dataArrIQ');
cc = diag(diag(inv(cm)).^(-1));
res = (cc / cm) * dataArrIQ;

Сначала вычисляется матрица автокорреляции входного сигнала. Затем эта матрица обращается и каждая строка обратной матрицы поэлементно делится на соответствующий ей диагональный элемент. Нормированная таким образом обратная матрица умножается на входной сигнал и в результате получается очищенный от помехи выходной сигнал. Смысл этой операции заключается в «декорреляции» сигналов, полученных с разных антенн и сильно коррелированных из-за присутствия помехи. Формула вычислений такая:

$\left(\begin{array}{c} y_1 \\ \vdots \\ \vdots \\ y_N \end{array}\right) = \left(\begin{array}{cccc} R_{11}^{-1} &0 &\ldots &0 \\ 0 &R_{22}^{-1} &\ldots &0 \\ \vdots &\vdots &\ddots &\vdots \\ 0 &0 &\ldots &R_{NN}^{-1} \end{array}\right) R \left(\begin{array}{c} x_1 \\ \vdots \\ \vdots \\ x_N \end{array}\right)$

Вот такой простой математикой можно вытащить GPS-приемник из пасти демона и получить вполне хороший SNR.

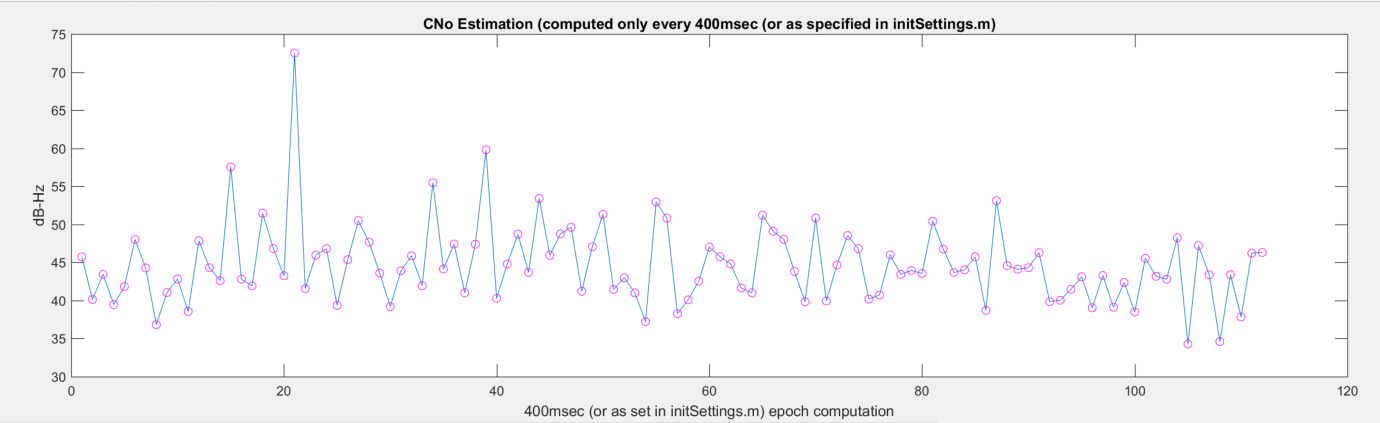
image

Есть один нюанс: так как помеха гармоническая, она может быть подавлена частотным фильтром, а не пространственным, без использования антенной решетки. Эта возможность сейчас встроена во все хорошие навигационные приемники. Компенсация гармонической помехи антенной решеткой рассмотрена нами с целью упрощения материала. Но это позволяет нам продемонстрировать принцип, который позволяет бороться и с широкополосными помехами. Компенсация широкополосных помех несколько сложнее. Мы надеемся рассказать о компенсации широкополосных помех в будущих публикациях.

Также недостатком представленного кода является интервал, на котором усредняются параметры помехи. Сейчас он равен длительности выборки. В реальности параметры меняются во времени и мы должны отслеживать эти изменения с нужным темпом.

Все рассказанное выше вы можете проделать сами. Код компенсатора берите из статьи. Код приемника от профессора Акоса здесь. Файлы с записями берите здесь. Не забудьте, они все вместе весят больше гигабайта.

Модифицируйте код, достигайте лучших результатов, публикуйте их. Кто знает, может быть кто-то из нас сможет приблизиться по характеристикам к лучшим изделиям отечественной промышленности, таким как это.

Большое спасибо за участие в подготовке этой статьи и кода в ней нашему математику-программисту vtsarik!

© Habrahabr.ru