Шапка-невидимка
/Давайте представим себе эдакую весьма неожиданную и необычную ситуацию, когда, прогуливаясь в чистом поле, мы вдруг обнаружили некий клад — сундук, полный всяких там драгоценностей. А почему бы и нет? Разве чудес на свете не бывает? Вот так вот — буквально голая степь, ни деревца, ни кустика. Одна лишь ёлочка произрастает поблизости и всё. А рядом прямо на поверхности травы стоит этот самый весьма дорогостоящий сундук, невесть кем и когда оставленный тут.
И схематически эта довольно-таки необычная ситуация отображена на рисунке 1 ниже. Так что предлагаю считать этот рисунок некой опорной точкой для всех предстоящих рассуждений и умозаключений.
 Рисунок 1.
Рисунок 1.
И всё бы тут ничего, но как на грех нами где-то вдалеке обнаружен некий незнакомый нам чужак, который пока ещё не заметил ни нас, ни клада. И, как это нетрудно догадаться в нынешней ситуации, ни малейших оснований для доверия к этому потенциальному свидетелю у нас не имеется. Скорее даже наоборот.
Правда отмечу, что этот незнакомец находится всё-таки далековато от нас, и поэтому он не вместился в рамки вышеприведённой схематической картинки. Но это вовсе не значит, что он вообще не существует, поскольку в любой момент может обнаружить нас и самое главное — нашу драгоценную находку. И тогда неизвестно, как развернутся все последующие события? Предлагаю для определённости считать, что он находится в правой части далеко за пределами изображения, откуда ему должен быть заметен наш сундук на фоне зелёной ёлочки.
Но снова как на грех у нас по каким-то тем или иным не зависящим от нас объективным причинам в данный весьма критический момент нет ни малейшей возможности забрать сундук с собой или, например, замаскировать его любым доступным способом. И остаётся только одно — каким-то образом скрыть этот клад от постороннего взора. На ёлочку этот потенциальный злопыхатель пусть любуется, сколько захочет. Но от нас требуется каким-то образом добиться, чтобы наша драгоценная находка оставалась для всех незаметной на фоне этой самой ёлочки.
Но тут даже дошкольник знает, что если уж вдруг потребовалось скрыть от посторонних глаз какой-нибудь объект, то его надо накрыть шапкой-невидимкой. Но только вот не надо пожалуйста насмехаться над детской наивностью, поскольку, как это известно, устами младенца очень даже часто глаголит самая банальная истина.
Поэтому предлагаю вполне по-взрослому и по-серьёзному сформулировать все необходимые технические требования к этой самой шапке-невидимке. Тем более, что их существует всего два:
шапка-невидимка должна быть незаметна сама по себе;
и при этом она должна скрывать расположенный под ней предмет.
Но вполне очевидно, что такого добиться крайне трудно. Например, если сделать такую шапку из прозрачного материала, то выполнения первого требования достичь удастся. Но всё это тем не менее не имеет ни малейшего практического смысла, поскольку второе требование по-прежнему не выполняется. Поэтому в данной ситуации надо поступить как-то иначе.
А что, если нам каким-то образом удастся заставить световые лучи, исходящие от одинокой ёлочки, огибать сундук, а потом возвращаться в исходное направление? Ведь в этом случае наблюдатель справа и в самом деле будет видеть одну лишь ёлку, и при этом — ни малейшего намёка на скрываемый перед ней объект. Схематически я эту ситуацию отобразил на рисунке 2, где световые лучи, исходящие от ёлки в правую сторону, где, напомню, находится незнакомец, образно отображены жёлтым цветом.
 Рисунок 2.
Рисунок 2.
Как видим, здесь каждый горизонтальный луч, трижды меняя своё направление и огибая тем самым скрываемый нами объект, снова возвращается к исходному направлению, как будто бы он никогда его не менял. Этим и создаётся обман зрения, благодаря чему огибаемый объект станет незаметным достаточно отдалённому наблюдателю справа.
«Но всё-таки, — вдруг вполне резонно спросите вы, — как далеко должен располагаться потенциальный наблюдатель, чтобы и в самом деле проявился эффект невидимости?» Математик, буквально мельком взглянув на эту принципиальную схему, вполне определённо ответит вам: «Бесконечно далеко», и будет в принципе совершенно прав. Но к счастью (или может к несчастью?) наш мир не столь уж идеален и точен, благодаря чему на практике хватит и стометрового расстояния. Правда даже эта цифра достаточно условна, поскольку во многом она зависит от размеров скрываемого объекта — в нашем случае сундука. Но мы всё равно чуть попозже, — когда предлагаемая мною модель уже будет окончательно обрисована в необходимых деталях, — поговорим о том, что же произойдёт на практике при недопустимом приближении нежелательного наблюдателя, и как можно будет попытаться решить эту проблему?
Однако математик или физик уже возможно заметил, что в процессе такого огибания увеличивается естественное расстояние, пройденное лучом от исходной точки до наблюдателя. Особенно это касается тех лучей, которые прорисованы ниже всего параллельно к уровню земли. Но по мере повышения горизонтального уровня этот эффект постепенно сводится на нет. Ну, а всё это вместе взятое приведёт к тому, что получаемое наблюдателем изображение будет немного запаздывать по времени, где нижняя часть изображения окажется наиболее устаревшей.
Но на практике это будет актуально лишь для особо динамичных объектов, просвечивающихся сквозь скрываемый предмет. Однако наша фоновая ёлочка очевидно не является объектом особой подвижности. Кроме того особо внимательный наблюдатель заметит этот релятивистский эффект лишь в том случае, если габариты нашего сундука будут составлять размеры от сотни тысяч километров и выше. Но мы ведь, будучи от рождения скромными людьми, вовсе не претендуем на такие космические масштабы. Не правда ли?
А теперь, собственно говоря, и подошло естественное время для вопроса:, а как можно на практике добиться такого огибания света. Современная наука знает несколько способов для изменения направления светового луча: например преломление или плавное изменение направления потока фотонов под сильным действием гравитационного или электромагнитного поля. Но всё это не совсем подходит для нашего случая, и остаётся лишь отражение света зеркальной поверхностью. Конечно же, в процессе такого отражения зеркало поглощает какую-то небольшую часть световой энергии. Но, как я уже говорил, ничего идеального в этом мире нет, и посему обычно приходится довольствоваться имеющимися возможностями.
Таким образом от нас с вами требуется построение такой криволинейной системы зеркал, которая бы и обеспечила продемонстрированный выше эффект обтекания. Строго говоря, для современной математики эта задача не представляет особой сложности. Но в рамках этой научно-популярной статьи мне едва ли дадут возможность приведения здесь математических формул и расчётов. К тому же там ничего особо сложного нет. Поэтому я на рисунке 3 привожу уже готовое решение этой прикладной математической задачи в виде системы криволинейных отражающих зеркал.
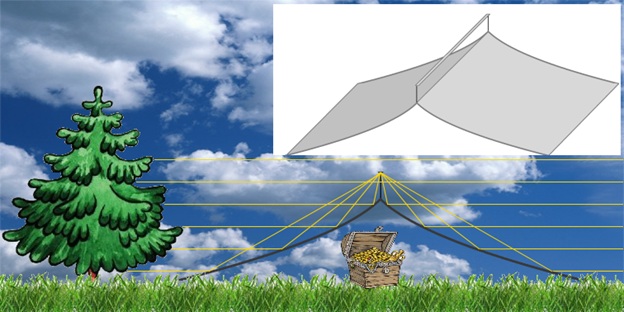 Рисунок 3.
Рисунок 3.
Эта система отображена на этой принципиальной схеме в вертикальном разрезе, а её объёмный ракурс для большей наглядности отображён там же в верхнем правом углу рисунка. Как видно отсюда, изображение в разрезе и в самом деле отдалённо напоминает широкополую шляпу, тогда как его же трёхмерное изображение больше похоже на свод криволинейной крыши. И в таком виде весь механизм трёхкратных зеркальных отражений вроде бы должен быть понятным, однако всё равно надо немного задержаться на верхнем горизонтальном плоском зеркальном рефлекторе
Всё дело тут в том, что, как это видно из вышеприведённой схемы, все горизонтальные световые лучи фокусируются там строго в одной математической точке. А это в свою очередь означает, что с позиций математики толщина этого рефлектора может быть нулевой. Однако в нашем материальном мире не существует твёрдых объектов без конкретного размера. И, каковой бы микроскопичной ни оказалась эта толщина в практической реализации, но она всё равно будет вполне осязаемой и возможно даже видимой. Тут всё дело в существующей на сегодняшний день технологии, и математика нам тут уже, увы, едва ли чем поможет.
Кроме того должны быть ещё какие-то боковые подпорки, удерживающие этот рефлектор навесу в требуемом положении. Так вот от технологов тут тоже потребуется добиться того, чтобы они тоже не бросались в глаза хотя бы уж с далёкого расстояния.
Математическое решение требует, чтобы между этим горизонтальным рефлектором и верхушкой свода существовал какой-то ненулевой просвет. Строго говоря, этого же требует и оптика, поскольку через это отверстие как раз и проходят все отражённые лучи света. Но дело тут не в этом, поскольку математически этот просвет не должен быть слишком уж узким, так как в этом случае форма свода при этом очень быстро становится почти что плоской и неспособной под собой укрыть более или менее крупный материальный объект. А в вырожденном математическом случае, когда этот просвет строго равен нулю, соответственная функция вообще вырождается в горизонтальную прямую или плоскость, если говорить об объёмной реализации этой системы. И по всем этим причинам на вышеприведённой схеме демонстрируется система, где высота этого злополучного зазора составляет 25% от общей высоты установки.
И ещё я пока не сказал, что математически этот свод можно продолжать и дальше — буквально до бесконечности — в обе стороны. В нашем случае — это уже под землю. Но даже, если при этом продолжении соответствующим образом приподнимать свод, это всё равно вскоре становится нерентабельным, поскольку этот свод постепенно становится всё более и более плоским, бессмысленно занимая при этом слишком уж большую площадь поверхности земли. Поэтому тут всё равно потребуется рано или поздно остановиться при достижении какой-то рациональности.
 Рисунок 4.
Рисунок 4.
В частности для большей наглядности я на рисунке 4 проиллюстрировал этот график для случая, когда высота зазора составляет всего 5% от общей высоты нашей оптической установки. Как это наверное хорошо заметно, в таком виде эта конструкция и в самом деле окажется слишком уж маловместительной и громоздкой по занимаемой ею площади.
И ещё наверняка многие уже заметили, что вышеприведённая система зеркал абсолютно симметрична по горизонтали. А это в свою очередь означает, что если удалённый потенциальный наблюдатель будет видеть одну лишь ёлку, то и ёлка, обладай она зрением, тоже видела бы этого наблюдателя прямо сквозь сундук с драгоценностями. Правда, в данном случае она расположена слишком уж близко к скрываемому нами объекту, а мы при этом даже приблизительно не знаем, где располагались бы глаза у этой гипотетической зрячей ёлки? Однако эти вопросы близости наблюдателя я уже повторно предлагаю отложить до более удачного момента.
Вместо этого подошёл черёд обсудить вопросы математической устойчивости найденного нами решения. Если говорить попросту, то насколько корректно будет функционировать эта система при изменении местоположения наблюдателя, на которого эта наша система сейчас буквально «нацелена». О математическом абстрактном бесконечно удалённом наблюдателе я сейчас не говорю, поскольку все его конечные перемещения ничего не изменят в общей системе функционирования.
А вот что произойдёт, если вполне материальный наблюдатель вдруг начнёт, например, движение по вертикали — буквально взлетать или взбираться на высокую гору. Да в этом случае и в самом деле система постепенно начнёт для него проявляться как бы из небытия — зеркала к примеру начнут отбрасывать световые блики и т.п. Поэтому оставлять её без присмотра нельзя, и кто-то должен постоянно следить за существенными перемещениями нежелательного наблюдателя, переориентируя наш зеркальный свод строго в его направлении и меняя тем самым положение всего приспособления вращением или наклоном в ту или иную сторону. Однако, согласитесь, что человек в качестве оператора тут даже не понадобится, поскольку со столь незамысловатыми манипуляциями очень даже легко справится современная электронная автоматика.
Итак, мы пришли к выводу, что сундук с драгоценностями всё-таки при определённых условиях можно спрятать от любопытных и нежелательных глаз. Но что увидит этот самый наблюдатель на месте, занятом невидимым сводом. Ведь форма свода вовсе не рассчитана нами на сокрытие этой площадки земной поверхности. А это в свою очередь означает, что на этом месте наблюдатель увидит лишь чёрное прямоугольное пятно в соответственном ракурсе зрения, которое в определённых случаях может и в самом деле выдать скрываемое нами местоположение.
Но, как оказалось, эта проблема очень даже легко решаема. Просто, как это видно из всех вышеприведённых схем, горизонтально симметричный свод будет корректно функционировать даже если, его перевернуть буквально вверх ногами. Причём никакого чёрного пятна на его месте в этом случае уже не будет наблюдаться. Однако вместо этого окажется видимой самая задняя внутренняя часть свода. Так вот, чтобы устранить ещё и этот недостаток, для достижения полной прозрачности достаточно будет накрыть эту конструкцию его зеркальной копией. И для большей наглядности всё это продемонстрировано на рисунке 5 чуть ниже.
 Рисунок 5.
Рисунок 5.
Конечно же, в данном случае, только что избавившись от одного досадного недочёта, мы сразу же приобрели вместо него новый недостаток. Просто теперь, как это наверняка нетрудно будет заметить, приходится каким-то образом обеспечить устойчивое положение этой достаточно неустойчивой конструкции так, чтобы все элементы этих подпорок были малозаметны хотя бы уж издали. Ведь это всё-таки — не какое-то там летательное приспособление, из-за чего и этот вопрос, в котором я к огромному моему сожалению совершенно некомпетентен, снова вынужденно переадресовывается мною технологам. Тем не менее, ничего технологически недостижимого тут всё равно пока не вижу
И вот наконец и наступило время, чтобы разобраться с тем, как поведёт себя наша оптическая система, если нежелательный наблюдатель всё-таки приблизился к ней на недопустимо малое расстояние. Правда перед этим потребуется выяснить, в чём тут принципиальная разница? Просто окуляр оптического прибора, равно как и зрачок глаза, воспринимают лишь те световые лучи, которые попали в их радиус.
Если вспомните, то наша установка рассчитывалась для беспрепятственной передачи горизонтальных параллельных между собой световых лучей. Однако такая схема лишь приближает бесконечно удалённого абстрактного наблюдателя, к которому все световые лучи от нашей установки и в самом деле приходят параллельными на такое немыслимое расстояние.
А, если взять реального наблюдателя на почтительном расстоянии, то к нему лучи приходят почти, однако не строго, параллельными. Тем не менее, на практике обычно существуют определённые допуски, которыми можно пренебречь без особого вреда для дела. Этим мы и пользовались до сих пор.
Но когда наблюдатель приближается слишком уж близко, пучок световых лучей всё меньше и меньше начинает напоминать параллельные линии. Говоря другими словами, максимально возможный допуск на погрешность когда-нибудь всё-таки зашкаливается. Впрочем, для большей наглядности я схематически отобразил эту ситуацию на рисунке 6, где, как и раньше, жёлтыми линиями образно отмечены световые лучи, сходящиеся к наблюдателю от фоновой ёлочки. Именно эти лучи и воспринимаются им, тогда как все остальные в данной ситуации можно без ущерба для дела проигнорировать.
 Рисунок 6.
Рисунок 6.
Очевидно, что наша оптическая установка, рассчитанная на параллельные лучи, в этом случае оказывается почти бесполезной, поскольку окажется достаточно хорошо заметной этому наблюдателю. И, чтобы снова добиться иллюзии прозрачности, нам придётся проводить другой расчёт для вычисления новой формы криволинейных зеркал. Кстати, в этом случае уже окажется потерянной симметрия свода по горизонтали, но это не столь уж и серьёзная потеря на мой взгляд.
Гораздо хуже тут то, что такой перерасчёт придётся производить всякий раз, как только изменится расстояние до наблюдателя. Получается, что наша зеркальная система должна уметь, подобно амёбе, адаптировать свою внешнюю форму почти под любые изменения окружающей обстановки. Однако эластичные зеркала — это пока, если я только не ошибаюсь, что-то из области фантастики. Так что, такой способ адаптации наверное всё-таки придётся отвергнуть буквально на корню как малоперспективный, поскольку в технологическом отношении, как вдруг оказалось, существует более простой и изящный способ.
И для этого нам придётся, оставив форму криволинейных зеркал неизменной, немного поманипулировать с горизонтальным рефлектором, слегка расширив его, например, в заднем направлении, чтобы дать ему возможность должным образом отражать теперь ещё и наклонные световые лучи, исходящие от нашей фоновой ёлочки. Таким образом, ширина этого рефлектора даже в математическом плане уже далеко не нулевая, что и отражено схематически на очередном рисунке 7. Так что отмечу, что лишь в этой весьма незамысловатой модернизации — единственное отличие от нашей первоначальной универсальной схемы, рассчитанной нами, если вспомните, на бесконечно удалённого абстрактного наблюдателя.
Правда, сундук с кладом, как это видно ниже, пришлось всё-таки переместить с его исходного места на поверхности почвы, поставив его внутри нашей оптической установки. Но, думается, что в данном случае это — не столь уж и принципиальный повод для придирок в мой адрес.
 Рисунок 7.
Рисунок 7.
Кстати, для того, чтобы данная оптическая система оставалось прозрачной в обоих направлениях просмотра, потребуется симметрично расширить плоские горизонтальные рефлекторы ещё и в правую сторону, что не отражено мною на вышеприведённой схеме. Стало быть, в таком виде эта система обеспечивает прозрачность лишь в одну сторону. Ну, а основная причина этой моей «недоделки» станет понятной чуть позже.
Итак, как теперь это видно, нам даже и в этом критическом случае удалось добиться от нашей установки иллюзии невидимости или прозрачности. Да, сундук с драгоценностями и в самом деле оказывается надёжно сокрытым от любопытных глаз наблюдателя. Да и система криволинейных зеркал оказывается тоже для него прозрачной. Но, вот лишь одна беда назревает в качестве небольшой ложки дёгтя для бочки мёда — достаточно широкие горизонтальные рефлекторы, отбрасывающие световые блики и совсем неуместные для нашей задачи зеркальные отражения фрагментов фоновой ёлочки, этому наблюдателю всё-таки будут заметны. И никуда от этого не денешься, особенно — на таком близком расстоянии. Именно поэтому я продлил рефлектор лишь в одном направлении, поскольку хотелось сделать его менее заметным и броским
Может быть, на этот недостаток и можно было бы закрыть глаза, например, замаскировав каким-то образом эти рефлекторы под какие-то материальные объекты или что-то в этом роде. Но, к сожалению, мне удалось обнаружить ещё одну «ложку дёгтя», о которой я, как человек честный и самокритичный, просто не имею права умолчать. Просто оказалось, что, наблюдатель, приблизившись к установке, увидит не только рефлекторы, но ещё и кое-что другое.
Всё дело тут в том, что до сих пор мы были в основном озабочены беспрепятственным прохождением световых лучей сквозь нашу оптическую установку, из-за чего почти на всех вышеприведённых схемах эта установка отображалась мною в горизонтальном продольном ракурсе, тогда как вид сверху нами пока не анализировался.
Но, казалось бы, чего тут может быть такого выдающегося? И так ведь вроде бы совершенно очевидно, что в этом ракурсе наша установка представляет собой прямоугольник, состоящий из двух симметричных частей. Однако предлагаю всё-таки не торопиться с поспешными выводами и повнимательнее присмотреться к нашей установке ещё и с этого ракурса. И на схематическом рисунке 8 всё это отображено наглядно.
Наблюдателя я расположил как и раньше — справа, но в данном случае мы смотрим на него сверху. То же самое касается и нашей зеркальной установки, которая по-прежнему располагается левее наблюдателя.
Так вот в этом ракурсе сразу же становится очевидным, что наша оптическая установка в нынешнем её состоянии передаёт наблюдателю на передний экран зеркального свода не всё фоновое изображение, которое загорожено от наблюдателя этим самым сводом. Просто часть боковых лучей, как это видно, тем или иным способом поглощается боковой частью свода. И эту зону «отчуждения» я для большей наглядности условно выделил на схеме особым розоватым полупрозрачным оттенком лишь только для того, чтобы она стала более заметной читателю этой статьи.
 Рисунок 8.
Рисунок 8.
Ну, а в результате того, что некоторые световые лучи от фонового изображения так и не доходят до наблюдателя, порождается визуальный эффект двух симметричных чёрных пятен по боковым краям переднего экрана установки, которые будут накладываться на фоновое изображение, загораживая его собой. Условно тут можно выразиться так, что это тень, отбрасываемая боковой «непрозрачной» частью нашей оптической установки.
На схематическом рисунке эти пятна смотрятся как чёрные прямоугольные треугольники, и аналогичным образом они будут смотреться в глазах наблюдателя. Только в его ракурсе они окажутся намного сильнее растянутыми по вертикали. Ну и естественно, если наша установка состоит из двух совмещённых сводов, как это было отображено в частности на рис. 7, то эти чёрные треугольники окажутся симметрично продублированными ещё и вниз, поскольку нижняя часть свода тоже будет оставлять свою собственную «тень»
И, чем ближе переместится наблюдатель к передней части установки, тем шире будут по горизонтали смотреться для него эти чёрные фигуры. И когда он, приближаясь дальше, наконец упрётся в нашу установку, черные треугольники для него вообще соприкоснутся друг с другом в самой широкой своей части.
Однако, как это видно на рисунке 8, от эффекта чёрных пятен всё-таки можно избавиться. Для этого потребуется, чтобы верхний ракурс нашей оптической установки представлял собой не прямоугольник, как сейчас, а симметричную трапецию, покрывающую собой зону «отчуждения» по бокам зеркального свода. В частности на последнем схематическом рисунке эта часть зоны «отчуждения» для наглядности слегка выделена яркостью. В этом случае все чёрные треугольные «тени» и в самом деле исчезнут, и свод установки снова станет для наблюдателя полностью прозрачным и невидимым. Но только вот беда, что форма и размеры этой трапеции полностью зависят от текущего положения этого столь непоседливого наблюдателя.
Ну что же, нам с вами на цепь его сажать, как какого-то дворового пса? Ну уж нет — ведь наше российское законодательство строжайше запрещает препятствовать свободному передвижению человека. И мы, как законопослушные граждане, обязанные уважать и чтить кодекс, просто не можем пойти на столь откровенный криминал ради достижения прозрачности нашей оптической установки.
Ну и плюс к этому — мы ведь ранее уже вроде бы договорились считать форму нашего оптического свода неизменной и незыблемой. Поэтому я больше не предлагаю механизм динамической адаптации формы свода под изменения местоположения наблюдателя.
Ну и что же из всего этого вытекает? Так вот, с огромным своим сожалением вынужден констатировать очевидное, что на достаточно близких расстояниях наша установка по тем или иным визуальным характерным признакам будет всё-таки заметна наблюдателю. Но всё-таки предлагаю проследить за тем, как она будет себя вести при его удалении?
Нетрудно заметить, что в этом случае чёрные «тени» начнут сужаться к краям переднего экрана и становится тем самым всё менее и менее заметными. Впрочем, почти то же самое касается и горизонтального плоского рефлектора, который в конечном счёте можно будет вернуть к его первоначальным «нулевым» размерам, рассчитанным для абстрактного бесконечно удалённого наблюдателя. И в какой-то не очень строго определённый момент времени установка снова станет почти полностью невидимой для наблюдателя. И даже бинокль едва ли поможет ему локализовать местоположение сундука с драгоценностями.
Напомню в связи с этим, что рассчитанная схема ориентирована во всех смыслах этого слова лишь на одного наблюдателя. А что произойдёт, если их много где-то там вдали? И растянулись они там многокилометровым фронтом? Увы — тут я тоже ничего поделать не могу. Искривление формы свода по дуге как бы для панорамного обзора тут совершенно бессмысленно, поскольку не только не даёт должного результата, а скорее даже наоборот — служит дополнительным средством привлечения постороннего внимания. Просто в этом случае боковые части сферически закруглённого свода начнут отбрасывать в глаза наблюдателей яркие зеркальные блики вроде солнечных зайчиков.
Так что идеальная шапка-невидимка у меня, как видите, увы, не получилась. Но, тем не менее, может быть получится у кого-нибудь из вас?
