Решение уравнения с целочисленным делением без перебора02.11.2018 14:32

Недавно на Тостере прозвучал вопрос, который не на шутку меня задел. Корнями он уходит в задачу, которую я приведу здесь в немного другой интерпретации:

Сдали как-то программисты проект в срок и получили премии. На радостях, прямо в ПН скинулись и на все деньги купили пива. В тот же день всё выпили, а во ВТ решили продолжить, но денег больше не осталось. Тогда они сдали бутылки, добавили вчерашнюю сдачу и снова затарились на все, как и вчера. То же проделали в СР и ЧТ. А в ПТ денег оказалось ровно на одну бутылку. Задумались — вспомнили цену одной бутылки, почём у них принимали тару (цены были без копеек), а сколько было денег изначально, никто назвать не смог. Проект был масштабный, премии большие — так что перебором не стоит. Каким же был минимальный бюджет в ПН, чтобы события сложились именно таким образом?

Рассуждая над ней следующим образом

спойлер
поскольку ребята каждый день покупали столько пива, сколько позволял им текущий бюджет (B, budget) — бюджет следующего дня (NB, next_day_budget) формировался из выручки от возврата тары и вчерашней сдачи. Две переменные сложнее одной, потому я перешёл к учёту ежедневного уменьшения бюджета (BL, budget_loss). Причём $BL = (P-R)N$, где P, price — стоимость одной бутылки пива; R, return — цена тары при возврате, а N — количество приобретённых за день бутылок, такое, что $N = B // P$. Тогда, можно заключить следующее:

$B = NB + (P-R)(B // P)$


я пришёл к уравнению, которое в абстрактном виде выгядит так (1):

$x = a(x // b) + c$

Пытаясь найти подход без перебора к решению такого рода уравнений я потратил не один час, но в итоге нашёл поистине чудесное решение, но поля книги слишком узки ;)

Без иллюзий на счёт первенства в этом вопросе, хочу лишь поделиться удовольствием, полученным в процессе. Если кто знает альтернативный метод или название этого, просветите меня; подобных мне призываю к обсуждению, а нетерпеливых — приглашаю под кат.
Рассмотрим полученное уравнение в таком виде (2):

$(x-c)/a = x // b$

поскольку правая часть может принимать только целочисленные значения, всё выражение имеет смысл лишь тогда, когда в левой части числитель кратен знаменателю. Из этого очевидно, что x мог бы иметь значения начиная с величины с и дальше с шагом a.

Тогда я рассмотрел уравнение (1) в виде двух функций $y1 = x$ и $y2 = a(x // b) + c$. При каком аргументе они пересекутся, таким и будет решение. Для примера я выбрал небольшие значения параметров таким образом, чтобы отобразить картину, как можно лучше. Итак, пусть a = 3, b = 7, c = 9.

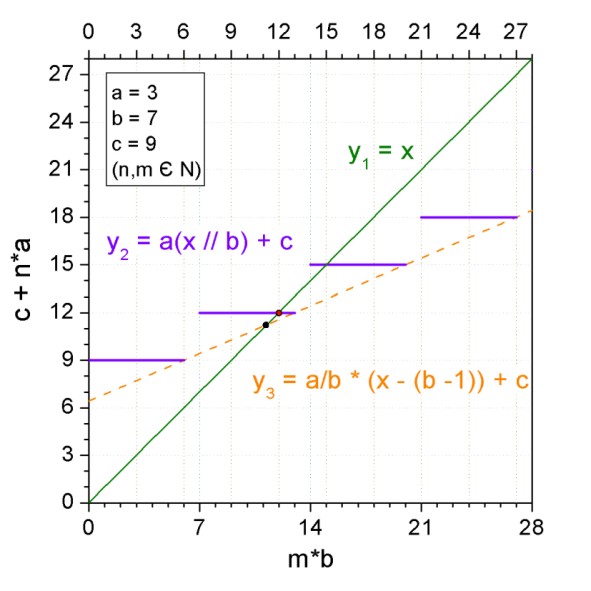
image


В силу ступенчатого характера второй функции графики y1 и y2 пересекаются в двух точках: при x1 = 12 и x2 = 15, но согласно условию, нас интересует именно первое значение, как меньшее. Так вот, для того, чтобы без перебора определить область пересечения, я ввёл третью функцию — это просто прямая, которая ограничивает функцию y2 снизу и имеет уравнение $y3 = a/b(x - (b-1)) +c$.

Теперь остаётся найти точку пересечения двух прямых (y1 и y3) и скорректировать ответ из ограничения на искомый x. Ведь исходя из условия, он может принимать только те значения, при которых соблюдается условие кратности числителя знаменателю в уравнении (2), т.е. $x = c + na$, где n — некий натуральный множитель. Для этого решим простое уравнение $x = a/b(x - (b-1)) + c$ и, если полученный корень не будет соответствовать нашим требованиям, сместим его до ближайшего подходящего. Поскольку вспомогательная функция y3 имеет положительный наклон, а все значения y2 находятся выше неё, то корректировку корня следует производить всегда в большую сторону. Так, в нашем случае, прямые пересекаются при x = 11.25 (чёрная точка на графике), и ближайшем большим значением, удовлетворяющим условие, будет 12 (красная точка), что и является ответом.

Поскольку в вопросе на Тостере стоял тег Python, ниже я приведу скрипт для решения этой задачи с использованием функции, для нахождения бюджета текущего дня на основании бюджета дня следующего. Применяем функцию нужное количество раз и, вуаля, получаем ответ! 

def this_day_budget(next_day_budget):
    a = bottle_price - tare_return_price
    b = bottle_price
    c = next_day_budget

    x = (a - a*b + b*c)/(b - a)
    if (x - c) % a:  # value does not match the increment
        x = ((x-c)//a + 1) * a + c
    return x

bottle_price = 7
tare_return_price = 4
party_duration_days = 5
last_day_budget = bottle_price

for days_to_party_end in range(party_duration_days):
    if days_to_party_end == 0:
        current_budget = last_day_budget
    else:
        current_budget = this_day_budget(current_budget)

print('first day budget was - %d' % current_budget)


Вместо заключения:

задачей в данном примере были обусловлены как значения параметров $a<b<c<x$, так и само уравнение $x=a(x//b)+c$; предлагаемый подход с небольшиими изменеиями применим и в других подобных случаях — целью публикации было лишь описание самого принципа без выведения универсального решения для общего случая — поэтому не судите строго (код на Python в т.ч.), и приятной всем пятницы!

© Habrahabr.ru