Решение систем линейных уравнений с помощью Python
Как-то я наткнулась на статью, где говорилось о SymPy— инструмент для решения систем уравнений, доступный на языке программирования Python. SymPy представляет собой бесплатную библиотеку для выполнения символьных вычислений. В отличие от численных методов, где компьютер манипулирует приблизительными числовыми значениями, символьные вычисления позволяют работать с уравнениями и выражениями, интерпретируя их как последовательность символов…

Учитывая, что линейные уравнения являются частью многих дисциплин, включая математику, физику, информатику и другие направления, я заинтересована в исследовании возможностей их решения с использованием Python.
Приятного прочтения)
Немного про систему линейных уравнений
Уравнение называется линейным, если оно содержит неизвестные только в первой степени и не содержит произведений неизвестных, т.е. если оно имеет вид , где
— коэффициент уравнения, а
— константа, не зависящая от x.
Система линейных уравнений объединяет n таких уравнений, каждое из которых содержит k переменных.
Визуально систему линейных уравнений можно представить следующим образом:
Системы линейных уравнений могут быть представлены в матричной форме , где
— это матрица коэффициентов системы линейных уравнений,
— вектор-столбец неизвестных, а
— вектор-столбец свободных членов. Библиотека SymPy предлагает функционал для работы с матрицами и позволяет решать системы уравнений через матричные операции.
Например, у нас есть система уравнений:
Предлагаю немного поиграть с ней и библиотекой.
Метод Крамера
Правило Крамера представляет собой ключевой метод для нахождения решений системы линейных уравнений. Этот метод опирается на вычисление определителей соответствующих матриц, поэтому его часто называют методом определителей. В контексте системы уравнений , где
— матрица коэффициентов, а
— столбец значений, правило Крамера выражает решение в виде отношения определителей, включающих матрицы, полученные заменой столбцов
на столбец
. Применять правило Крамера можно только в случае, если определитель матрицы
отличен от нуля, что указывает на её обратимость.
from sympy import symbols, Matrix
# Функция применения метода Крамера для решения системы линейных уравнений
def cramer_rule(A, B):
# Вычисление определителя главной матрицы
det_A = A.det()
# Проверка на случай, если определитель главной матрицы равен нулю
if det_A == 0:
raise ValueError("Определитель матрицы коэффициентов равен нулю, метод Крамера не применим.")
solutions = []
# Проходим по каждому столбцу матрицы и вычисляем определитель со заменой столбца на вектор значений
for i in range(A.shape[0]):
Ai = A.copy()
Ai[:, i] = B
solutions.append(Ai.det() / det_A)
return solutions
# Объявление символьных переменных
x1, x2, x3, x4 = symbols('x1 x2 x3 x4')
# Матрица коэффициентов системы уравнений
A = Matrix([
[1, 1, 1, 1],
[5, -3, 2, -8],
[3, 5, 1, 4],
[4, 2, 3, 1]
])
# Вектор значений
B = Matrix([0, 1, 0, 3])
try:
# Вызов функции для решения системы уравнений методом Крамера
solutions = cramer_rule(A, B)
# Вывод результатов
print("Решение методом Крамера:")
for i, sol in enumerate(solutions, start=1):
print(f"x{i}: {sol}")
except ValueError as e:
# Вывод сообщения об ошибке, если определитель главной матрицы равен нулю
print(e)

В коде представлена функция под названием cramer_rule, предназначенная для применения правила Крамера при решении систем линейных уравнений. Она сначала рассчитывает определитель основной матрицы , затем создаёт альтернативные матрицы, подменяя каждый из столбцов матрицы
вектором констант
вычисляя их определители. Решения переменных
получаются путём деления определителей этих альтернативных матриц на определитель основной матрицы
.
Затем в коде происходит объявление символьных переменных, а также формирование матрицы коэффициентов и вектора-столбца
, что необходимо для проверки эффективности правила Крамера.
В рамках блока try-except осуществляется вызов функции cramer_rule, чтобы найти решение системы уравнений с использованием метода Крамера. В случае, когда определитель основной матрицы оказывается равным нулю, происходит возбуждение исключения ValueError с последующим отображением соответствующего сообщения о невозможности решения. Если же определитель не равен нулю, результаты, представляющие собой решения системы, выводятся на экран.
Метод Гаусса
Метод Гаусса, известный также как гауссово исключение или преобразование системы уравнений к ступенчатой форме, представляет собой один из фундаментальных подходов к решению систем линейных уравнений. Этот метод включает выполнение элементарных операций над строками матрицы уравнений для её трансформации в ступенчатый или упрощённый ступенчатый вид, что значительно облегчает нахождение решений системы.
from sympy import Matrix, pprint
def print_row_reduced_matrix(matrix):
print("Ступенчатая матрица:")
pprint(matrix)
# Определение расширенной матрицы [A|B]
augmented_matrix = Matrix([
[1, 1, 1, 1, 0],
[5, -3, 2, -8, 1],
[3, 5, 1, 4, 0],
[4, 2, 3, 1, 3]
])
# Выполнение приведения матрицы к ступенчатому виду
row_reduced_matrix, _ = augmented_matrix.rref()
# Вызов функции для вывода ступенчатой матрицы
print_row_reduced_matrix(row_reduced_matrix)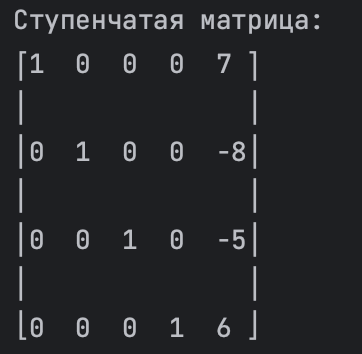
В представленном коде начинаем с определения расширенной матрицы, где в последнем столбце размещены свободные члены системы уравнений. Далее, используя метод .rref(), который предоставляется объектом Matrix библиотеки SymPy, преобразуем эту матрицу к ступенчатому виду.
После преобразования ступенчатая матрица отображается на экране с помощью функции print_row_reduced_matrix, что позволяет наглядно оценить изменения в структуре матрицы после применения метода Гаусса и определить лидирующие элементы.
Численное решение
Численное решение системы уравнений представляет собой процесс определения приблизительных значений переменных, когда точное аналитическое решение недостижимо или нежелательно. Этот подход часто используется в ситуациях, когда необходимо получить численное приближение для решения системы.
from sympy import symbols, Eq, nsolve
# Определение переменных
x1, x2, x3, x4 = symbols('x1 x2 x3 x4')
# Определение системы уравнений
equations = [
Eq(x1 + x2 + x3 + x4, 0),
Eq(5*x1 - 3*x2 + 2*x3 - 8*x4, 1),
Eq(3*x1 + 5*x2 + x3 + 4*x4, 0),
Eq(4*x1 + 2*x2 + 3*x3 + x4, 3)
]
# Начальное предположение для численного решения
initial_guess = [0, 0, 0, 0]
# Нахождение численного решения
numerical_solution = nsolve(equations, (x1, x2, x3, x4), initial_guess)
# Вывод результатов
print("Численное решение:")
print(f"x1 = {numerical_solution[0]}")
print(f"x2 = {numerical_solution[1]}")
print(f"x3 = {numerical_solution[2]}")
print(f"x4 = {numerical_solution[3]}")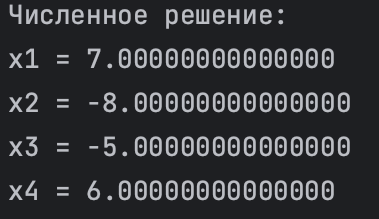
Код, который мы рассматриваем, задействует функцию nsolve из библиотеки SymPy для определения численного решения набора уравнений. Вначале определяются переменные x1, x2, x3 и x4 как символы. Далее, система уравнений представлена списком экземпляров Eq. Затем указывается начальное приближение для решения, представленное списком initial_guess.
Функция nsolve требует на вход список уравнений (equations), перечень символьных переменных (x1, x2, x3, x4) и начальное приближение (initial_guess). Она выполняет вычисление численного приближения значений переменных, которое максимально приближено к аналитическому решению, и возвращает полученные значения в форме списка.
Каждое найденное численное значение переменных x1, x2, x3 и x4 выводится отдельной строкой.
Метод наименьших квадратов
Метод наименьших квадратов — это статистическая процедура, применяемая для оптимального приближения данных. Она заключается в поиске такой функции, которая минимизирует общую сумму квадратов разности между фактическими значениями и значениями, предсказанными моделью. Этот метод особенно полезен при работе с переопределёнными системами линейных уравнений, то есть когда число уравнений превосходит число неизвестных.
from sympy import symbols, Matrix
# Определение переменных
variables = symbols('x1 x2 x3 x4')
# Определение матрицы коэффициентов
coefficients_matrix = Matrix([
[1, 1, 1, 1],
[5, -3, 2, -8],
[3, 5, 1, 4],
[4, 2, 3, 1]
])
# Определение матрицы значений
constants_matrix = Matrix([0, 1, 0, 3])
# Решение системы с помощью метода наименьших квадратов
least_squares_solution = coefficients_matrix.solve_least_squares(constants_matrix)
# Вывод решения
print("Решение методом наименьших квадратов:", least_squares_solution)
Здесь мы применяем функцию solve_least_squares от объекта Matrix библиотеки SymPy для решения системы линейных уравнений с избытком условий с использованием метода наименьших квадратов. Сначала вводятся переменные x1, x2, x3 и x4. Затем создаются матрицы: одна для коэффициентов (coefficients_matrix) и одна для свободных членов (constants_matrix) системы уравнений.
Функция solve_least_squares принимает эти две матрицы и находит вектор решений, который минимизирует сумму квадратов расхождений между произведением матрицы коэффициентов на вектор решений и реальными данными, содержащимися в матрице свободных членов.
Символьное решение
Символьное решение системы уравнений — это подход, при котором переменные обрабатываются как символы, и применяются математические алгоритмы для получения их точных аналитических значений. В отличие от численных методов, при которых значения переменных находят в числовом виде, символьное решение выдаёт формулы для переменных, возможно, включающие в себя другие символы.
from sympy import symbols, Eq, solve
# Определение переменных
x1, x2, x3, x4 = symbols('x1 x2 x3 x4')
# Определение системы уравнений
equations = [
Eq(x1 + x2 + x3 + x4, 0),
Eq(5*x1 - 3*x2 + 2*x3 - 8*x4, 1),
Eq(3*x1 + 5*x2 + x3 + 4*x4, 0),
Eq(4*x1 + 2*x2 + 3*x3 + x4, 3)
]
# Решение системы символьно
symbolic_solution = solve(equations, (x1, x2, x3, x4))
# Вывод решения
print("Символьное решение:", symbolic_solution)

В демонстрируемом коде начинают с определения символьных переменных x1, x2, x3 и x4, после чего уравнения системы формируются в коллекцию объектов Eq. Для символьного решения системы используется функция solve из библиотеки SymPy. Эта функция получает на вход список уравнений (equations) и список соответствующих символьных переменных (x1, x2, x3, x4), а возвращает словарь с аналитическими решениями для каждой из переменных.
В данной статье мы рассмотрели одну из функций библиотеки SymPy: решение систем линейных уравнений с использованием разных методов, выбор которых определяется конкретными задачами.
С точки зрения студента, важно не просто знание этих методов, важно глубокое понимание и умение применять их на практике, поскольку это может стать ценным опытом во многих областях науки и инженерии.
Выбор библиотеки SymPy для обзора был не случаен: она позволяет проводить символьные вычисления, обрабатывая выражения как серии символов, что значительно повышает точность математических операций. К тому же библиотека охватывает разнообразные сектора математики, включая решение уравнений и работу с матрицами. Дополнительным плюсом является её совместимость с другими инструментами, например с библиотекой Matplotlib, благодаря чему SymPy легко интегрируется для расширения своих возможностей.
Спасибо за прочтение)
