Репликация без конфликтов: CRDT в теории и на практике
В распределённых хранилищах или редакторах каких-либо данных часто бывает нужна поддержка внесения изменений оффлайн, без блокировок и конфликтов. Для этого применяются разные подходы, один из которых — алгоритмы и типы данных conflict-free replicated data type (CRDT).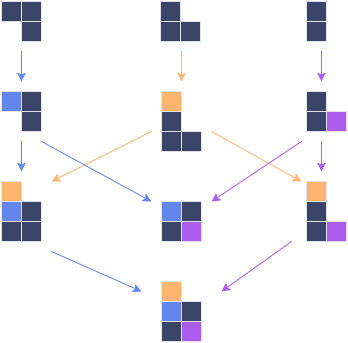
Сделать readonly-реплику просто и всем понятно, как. Возможность записи в реплику — сложная штука. Есть такая теорема CAP: согласованность данных (consustency), доступность (availability), устойчивость к разделению (partition tolerance) — выберите любые два. В CRDT эта задача решается обеспечением strong eventual consistency (SEC) и монотонности состояний.
Предположим, в реплики можно вносить изменения, которыми они каким-то способом обмениваются. Eventual consistency называется такая организация взаимодействия и хранения данных, при которой все реплики после прекращения внесения в них изменений когда-нибудь в конечном счёте придут в эквивалентное состояние.
Strong Eventual Consistency накладывает ещё одно ограничение: реплики, получившие одинаковые апдейты (не важно, в каком порядке), приходят в эквивалентное состояние немедленно после получения апдейтов.
Не надо путать SEC и последовательную консистентность (sequential consistency): допустим, в список, в котором можно добавлять и удалять элементы, не обязательно должен гарантировать последовательность добавление-удаление, чтобы удовлетворять SEC (например, может быть приоритет удаления надо добавлением).
В EC-системе могут быть конфликты. Конфликт — это изменения, которые будучи применёнными к разным репликам, приводят их в консистентное состояние, но при объединении состояний реплик нарушается некий системный инвариант. Конфликты разрешаются откатами состояний или другими способами, которые могут предполагать даже взаимодействие с пользователем.
В CRDT предполагается, что система обеспечивает SEC и её состояния монотонно прогрессируют, не приводя к конфликтам. Монотонность в этом смысле означает отсутствие откатов: операции нельзя отменить, вернув систему в раннее состояние. Состояния такой системы связаны отношением частичного порядка, в математике такая система с определённой на ней операцией объединения называется полурешёткой.
Полурешётка — это полугруппа, бинарная операция в которой коммутативна и идемпотентна (формальное объяснение есть в википедии, на русском и более подробно на английском, а тут с математикой).
Полурешётка — частично упорядоченное множество: элементы (не обязательно все) связаны отношением «следует за».
На полурешётке определена операция:
- идемпотентная: a ⋁ a = a
- ассоциативная: (a ⋁ b) ⋁ c = a ⋁ (b ⋁ c)
- коммутативная: a ⋁ b = b ⋁ a
Эта операция может быть или точной верхней гранью (least upper bound, LUB) для верхней (join) полурешётки, или точной нижней гранью (greatest lower bound) для нижней (meet) полурешётки.
Отличие дерева от полурешётки: 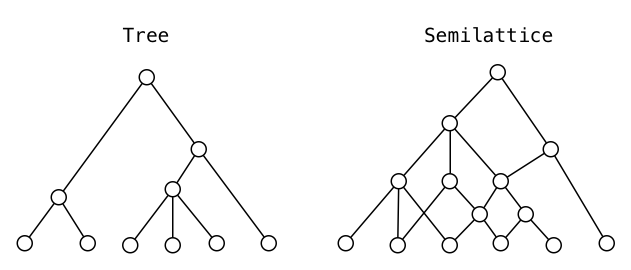
А это полная решётка, на ней определены и LUB, и GLB одновременно: 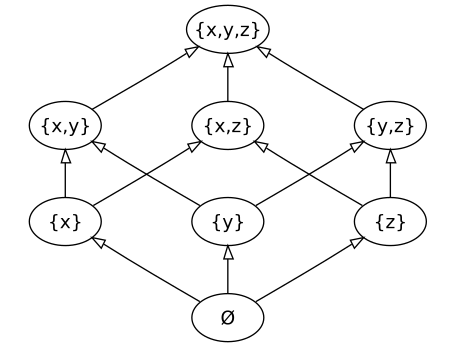
Пример верхней полурешётки изображён на КДПВ. Отличие в том, что для объединения элементов общий предок не обязателен. Вот такие алгебраические структуры нас сейчас и интересуют.
Множество состояний в системах контроля версий, таких как git или svn, представляют собой в некотором смысле полную решётку: на них определено отношение частичного порядка, ревизии имеют общего предка и могут быть смёржены. С элементами верхней полурешётки можно выполнить операцию join, сделав из двух элементов их объединение.
Для разных задач удобны разные способы организации взаимодействия и хранения данных. CRDT принято разделять на два класса:
- Коммутативные (commutative, CmRDT, op-based): предположим, у вас есть список. При добавлении элемента вы отправляете всем репликам только это измененённое состояние (добавленный элемент). Операции должны быть коммутативными, чтобы состояние реплики не зависело от порядка получения апдейтов.
- Основанные на хранении состояния (convergent: CvRDT, state-based): в этом случае отправляются не отдельные апдейты, а вся структура данных целиком (то есть, весь список, в случае списка). Структура данных должна поддерживать операции:
- query — прочитать что-то, не изменяя состояние (например: есть ли элемент в списке?)
- update — изменить структуру (например: добавить элемент в список)
- merge — замёржить состояние, пришедшее из другой реплики. Эта операция должна быть коммутативной, ассоциативной и идемпонетной: мёрж любых состояний в любых направлениях не «возвращает» систему в более раннее состояние, а монотонно увеличивает состояние системы. Если объединить все реплики, они должны прийти в эквивалентное состояние, объединяющее в себе все изменения, сделанные в репликах.
Наглядное сравнение: 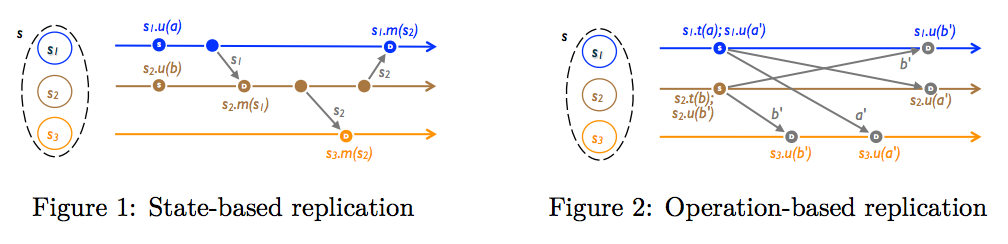
Классы CvRDT и CmRDT эквивалентны (доказательство этой теоремы есть в работе Marc Shapiro в «ссылках» внизу). Любую структуру CRDT можно представить и как CvRDT, и как CmRDT.
Однако с точки зрения требований к способу передачи данных, они разные: CmRDT требуют какого-либо способа доставки уведомлений репликам, в то время как всё, что нужно CvRDT — записать и прочитать состояние (но это состояние может быть достаточно большого размера).
Давайте сделаем список, в котором можно добавлять и удалять элементы. Он называется 2P-Set.
На реплике лежит два множества: добавленные элемент (A) и удалённые (R; это множество часто называют tombstone set), изначально пустые. При добавлении элемента, мы добавляем его в A, при удалении — в R. Проверка включения во множество состоит в проверке, нет ли элемента в R и есть ли он в A. Получается, удаление приоритетнее добавления: единожды удалив элемент, его уже нельзя добавить обратно: из R и A элементы не удаляются.
Математическая запись выглядит так: 
Это CvRDT-структура, которая для выполнения каждой операции передаёт весь список. Очевидным способом её можно сконвертировать CmRDT-эквивалент. Для простоты предположим совсем простой случай, когда add доставляется всегда до remove. Математическая запись CmRDT выглядит так:
payload — то, что расположено на реплике
initial — его начальное состояние
query — запрос состояния системы, не изменяющий её, выполняется локально на реплике
update — операция, изменяющая состояние системы
atSource — часть апдейта, которая выполняется на реплике-инициаторе
downstream — апдейты, которые будут выполнены на репликах для этой операции

Из известных, описанных в работах и реализованных в библиотеках, есть такие структуры:
- G-Counter: (grow-only) монотонно увеличивающийся счётчик
- PN-Counter: (positive-negative) счётчик, который можно уменьшать
- LWW-Register: (last-writer-wins) регистр с принципом последняя запись приоритетнее
- MV-Register: (multi-value) регистр с несколькими значениями
- G-Set: множество элементов без удаления
- 2P-Set: с приоритетным удалением
- PN-Set: использует счётчик операций включения-удаления
- LWW-Set: с приоритетом времени операции
- OR-Set: (observed-remove) список с идентификаторами
Есть ещё структуры, описывающие вершины и связи в графах, основанные на списках.
Обычный способ сделать CRDT-структуру — собрать её из других: например, 2P-set состоит из двух списков: добавленные и удалённые. На практике могут встретиться ограничения, накладываемые на операцию или объём передачи данных. В этом случае можно пойти на некоторые уступки. Например, если в список часто добавляются и удаляются элементы, список удалённых со временем сильно разрастётся. Можно сделать сборщик мусора, который бы удалял удалённые по какому-то разумному условию. Например, те, что удалены более года назад или те, нотификации о которых получили все реплики.
Operational Transformation — подход, применяемый обычно в редактировании текста. Оба подхода обеспечивают консистентность (EC). У OT более высокие требования к серверу, более сложные и менее стабильные алгоритмы. Также, в некоторых исследованиях показано, что алгоритмы OT иногда не сходятся (converge), как это заявлено в реализации. Однако однозначно сделать выбор и сказать, «что лучше», нельзя. Из известных CRDT редактирования текста есть, например, WOOT (WithOut Operational Transformation), Treedoc и Logoot.
В KeePass есть функция мёржа с файлом, мне в моей веб-версии надо было уделить мёржу особое внимание, чтобы сделать человеческий оффлайн с синхронизацией. KeePass назначает всем объектам уникальные идентификаторы и хранит ID всего удалённого в DeletedObjects. Для синхронизации графа директорий, в них хранится дата последнего изменения положения (location change date).
Но есть нюанс. У записей ещё есть история изменения, откуда можно удалять элементы. Записи в истории идентифицируются только по времени. Удалённые записи из истории никуда не сохраняются и при синхронизации. Что же это получается? Если удалить запись из истории и засинкать с предыдущим состоянием, она волшебным образом вернётся. Получается, в условиях синхронизации как основного сценария работы приложения история будет частенько появляться обратно.
Что делать?
Т.к. на другие клиенты повлиять нельзя, можно ввести ограничения. Рассмотрим те допущения, которые мы можем принять:
- файлы синхронизируются через центральное хранилище, а не p2p
- вместе с файлом всегда можно хранить любые метаданные на реплике
Исходя из этого, было принято решение с момента внесения изменений в файл до отправки изменений в хранилище хранить список удалённых и добавленных состояний истории (local tombstone set). При этом, конечно синхронизация с произвольными p2p-файлами из прошлого всё равно будет странной, но это уже не основной сценарий.
Для отправки изменений в хранилище клиент должен:
- сравнить ревизию файла (versionTag) с последней полученной
- если она изменилась, загрузить и замёржить
- если есть локальные изменения, залить с проверкой versionTag
- в случае конфликта goto 2
- очистить локальное состояние (tombstone set)
CRDT — Wikipedia
Readings in CRDT — много полезных публикаций про CRDT
CRDT — A digestible explanation with less math (GitHub) — небольшое описание CRDT без математики
crdt_notes (GitHub) — алгоритмы CRDT, собранные на одной страничке
Conflict-free replicated data types (paper) — введение в CRDT
A comprehensive study of Convergent and Commutative Replicated Data Types (paper) — подробное объяснение в деталях, с математикой и картинками, на 40 страниц
An optimized conflict-free replicated set — пример оптимизации структуры CRDT
kdbxweb (GitHub) — js-либа для работы с форматом KeePass с поддержкой мёржа, о которой шла речь
