Рекурсивный фильтр скользящего среднего

Да, дорогой читатель, такое тоже бывает, и может быть вкусно и полезно!
Как ты уже наверняка знаешь, дорогой читатель, существует два способа построения цифровых фильтров. Это рекурсивные фильтры, они же фильтры с бесконечной импульсной характеристикой (БИХ), и трансверсальные фильтры, они же фильтры с конечной импульсной характеристикой (КИХ). Самым простым и широко используемым фильтром КИХ является «фильтр скользящего среднего». Результат фильтрации такого фильтра, есть среднее арифметическое последних N отсчетов входного сигнала.

Или, в развернутом виде, для N=4:
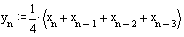
Функция на языке С реализующая фильтр скользящего среднего:
#define N (4)
int filter(int a)
{
static int m[N];
static int n;
m[n]=a;
n=(n+1)%N;
a=0;
for(int j=0;jКомплексный коэффициент передачи фильтра скользящего среднего, нормированный относительно частоты дискретизации, определится как преобразование Фурье от импульсной характеристики:
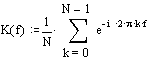
График амплитудно-частотной характеристики (АЧХ), нормированной относительно частоты дискретизации, при различных значениях длинны фильтра (N=4;8;16), приведен на рисунке:
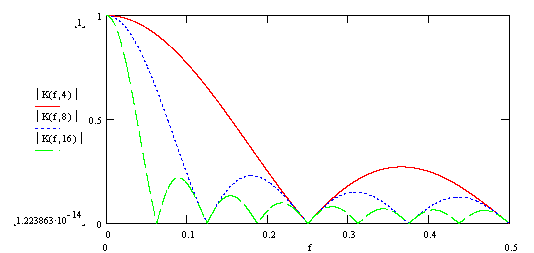
Соответственно, график фазо-частотной характеристики (ФЧХ):
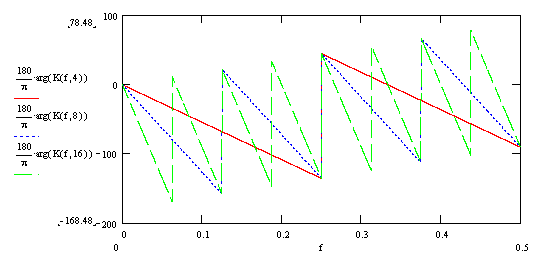
Данный фильтр нашел широкое применение в обработке сигналов, отчасти благодаря своей простоте, но самое главное его свойство — линейная фазо-частотная характеристика, и, соответственно, постоянное во всей полосе частот время запаздывания сигнала. Этот фильтр трансформирует амплитудный спектр сигнала, не затрагивая фазовый, что делает удобным его использование в системах регулирования. Фильтр скользящего среднего, благодаря своей линейной переходной характеристике, широко применяется при линейной интерполяции, передискретизации сигнала и т.п.
Главный недостаток фильтра скользящего среднего — вычислительная сложность, пропорциональная длине фильтра N. Для решения этой проблемы существует рекурсивный фильтр скользящего среднего. То есть, фильтр, имеющий те же характеристики, что и классический фильтр скользящего среднего, но реализованный по рекурсивной схеме. Такие типы фильтров широко известны в узких кругах, и называются: рекурсивные фильтры с линейной ФЧХ [Введение в цифровую фильтрацию. Под. ред. Богнера Р. М: 1976] или CIC-фильтры [DspLib]. Существует научная школа проф. Турулина И.И. [РГБ], занимающаяся исследованием подобных фильтров.
Покажем способ построения рекурсивного фильтра скользящего среднего на примере фильтра длинной N=4. Впоследствии нетрудно будет обобщить результаты на произвольную длину фильтра.
Как было отмечено выше, значение n-ного отсчета сигнала на выходе фильтра можно определить как:
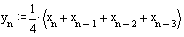
А значение предыдущего, ((n-1)-го) отсчета:
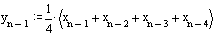
Вычтем из первого выражения второе, в результате получим:
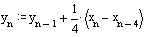
Нетрудно сообразить, что при произвольной длине фильтра N, уравнение запишется в следующем виде:
 (1)
(1)
На основании приведенного уравнения можно записать код фильтра на языке С, но сначала мы выполним проверку наших выкладок. Найдем частотные характеристики рекурсивного фильтра скользящего среднего, для чего выполним Z-преобразование уравнения фильтра. Хочу напомнить дорогому читателю, что для выполнения Z-преобразования необходимо заменить переменные (xn, yn) их Z-отображениями (X, Y), каждое понижение индекса переменной на единицу соответствует умножению Z-1.
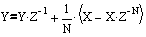
Решим полученное уравнение относительно Y/X –коэффициента передачи фильтра
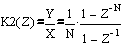
Перейдем из Z-области в частотную область, заменив 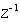 на
на 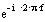 , и получим комплексный коэффициент передачи:
, и получим комплексный коэффициент передачи:
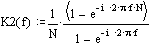
Построим график модуля комплексного коэффициента передачи (АЧХ фильтра), при различных значениях N=4,8,16:

А также аргумент комплексного коэффициента передачи (ФЧХ фильтра):

Как видно из приведенных графиков, частотные характеристики классического фильтра скользящего среднего и рекурсивного фильтра скользящего среднего полностью совпадают.
Перейдем к реализации фильтра. При непосредственной реализации по уравнению фильтра (1) в условиях целочисленной арифметики возможны некоторые трудности. При выполнении операции деления на N в целочисленной арифметике возникает потеря значащих разрядов, что приводит к нелинейным искажениям сигнала на выходе фильтра. Для разрешения этих трудностей необходимо исключить операцию деления из рекуррентного уравнения фильтра. Для чего умножим обе части уравнения фильтра (1) на N.
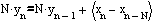
В полученном выражении выполним подстановку:
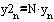

В результате уравнение фильтра (1) преобразуется в систему уравнений:

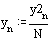
На основании системы уравнений фильтра запишем код, реализующий фильтр на языке С.
#define N (4)
int filter(int x)
{
static int n;
static int m[N];
static int y;
y=y+(x-m[n]);
m[i]=x;
n=(n+1)%N;
return y/N;
}Стоит отметить, что любители «совершенного кода» могут наложить ограничивающие требования на длину фильтра N. При длине фильтра, равной степеням двойки (2,4,8,16…), можно заменить операцию деления (/) арифметическим сдвигом (>>), операцию остаток от деления (%) — побитовой конъюнкцией (&).
Заключение.
Дорогой читатель, целью данной публикации не столько познакомить тебя с рекурсивным фильтром скользящего среднего, очень может быть, что ты про него прекрасно знаешь. Цель данной публикации познакомить тебя, дорогой читатель, с некоторыми практическими приемами анализа и синтеза цифровых фильтров. Посмотри, как просто мы перешли от трансверсального фильтра к рекурсивному, и Z-преобразование не так страшно, как его малюют. Надеюсь также, что метод повышения точности вычисления рекуррентных выражений в условиях целочисленной арифметики будет полезен тебе.
Успехов тебе, дорогой читатель!
Комментарии (4)
4 апреля 2017 в 09:45
0↑
↓
Ещё одна очевидная проблема рекурсивного фильтра — малейшее однократное повреждение данных приводит к перманентному искажению результата, а оно в реальных системах может произойти по разным причинам — космическое излучение, несанкционированная запись в область памяти массива со значениями и т.д. поэтому для надёжности иногда приходится пересчитывать по полной весь массив. Или должна быть какая-то обратная связь которая устранит расхождение.4 апреля 2017 в 09:48
0↑
↓
«Главный недостаток фильтра скользящего среднего — вычислительная сложность, пропорциональная длине фильтра N.» — ну надо ж было ляпнуть такую ерунду. Вычислительная сложность — одно сложение, одно вычитание, одно деление на константу (заменяется на умножение, а то и на сдвиг). O (1).
Вот памяти O (N) надо, это да. Поэтому на совсем мелких девайсах непопулярен. И других недостатков хватает.4 апреля 2017 в 10:00
0↑
↓
Автор имел в виду нерекурсивный фильтр (т.е. функция от предыдущих N входных отсчетов) —, а он реализуется как сумматор-делитель всех отсчетов, со сложностью O (N).
4 апреля 2017 в 10:00
0↑
↓
Зачем переменные static? это не позволяет делать в программе 2 параллельных фильтра.
