Реализация целочисленного БПФ на ПЛИС
Всем привет!
Однажды меня спросили заказчики, нет ли у меня в проектах целочисленного БПФ, на что я всегда отвечал, что это уже сделано другими в виде готовых, хоть и кривых, но бесплатных IP-ядер (Altera / Xilinx) — берите и пользуйтесь. Однако, эти ядра не оптимальны, обладают набором «особенностей» и требуют дальнейшей доработки. В связи с чем, уйдя в очередной плановый отпуск, который не хотелось провести бездарно, я занялся реализацией конфигурируемого ядра целочисленного БПФ.
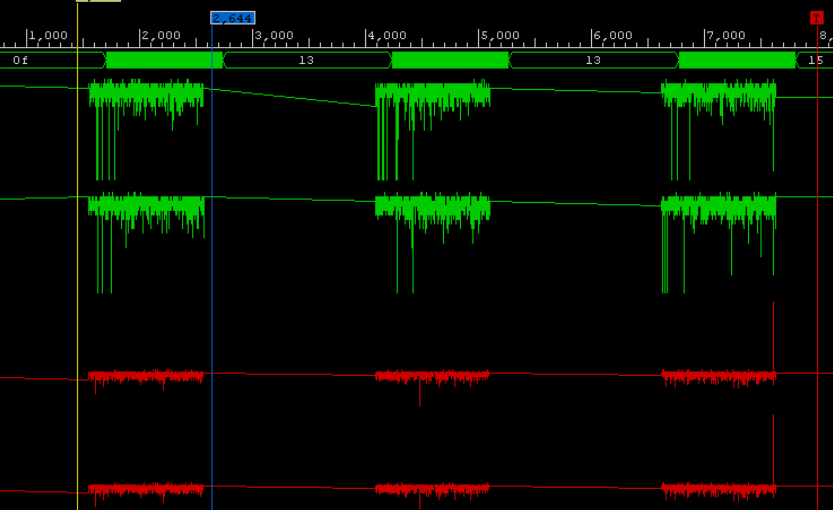
КДПВ (процесс отдладки ошибки переполнения данных)
В статье я хочу рассказать, какими способами и средствами реализуются математические операции при вычислении быстрого преобразования Фурье в целочисленном формате на современных кристаллах ПЛИС. Основу любого БПФ представляет узел, который носит название «бабочка». В бабочке реализуются математические действия — сложение, умножение и вычитание. Именно о реализации «бабочки» и её законченных узлов будет идти рассказ в первую очередь. За основу взяты современные семейства ПЛИС фирмы Xilinx — это серия Ultrascale и Ultrascale+, а также затрагиваются старшие серии 6- (Virtex) и 7- (Artix, Kintex, Virtex). Более старшие серии в современных проектах — не представляют интереса в 2018 году. Цель статьи — раскрыть трудности и особенности реализации кастомных ядер цифровой обработки сигналов на примере БПФ.
Введение
Ни для кого не секрет, что алгоритмы взятия БПФ прочно вошли в жизнь инженеров цифровой обработки сигналов, а следовательно, этот интрумент нужен постоянно. У топовых производителей FPGA, таких как Altera / Xilinx уже есть гибкие конфигурируемые ядра FFT / IFFT, однако они имеют ряд ограничений и особенностей, в связи с чем мне уже не раз приходилось пользоваться собственными наработками. Вот и в этот раз мне пришлось реализовать БПФ в целочисленном формате по схеме Radix-2 на ПЛИС. В своей прошлой статье я уже делал БПФ в формате с плавающей точкой, и оттуда вы знаете, что в для реализации БПФ применяется алгоритм с двухкратным параллелизмом, то есть ядро может обрабатывать два комплексных отсчета на одной частоте. Это ключевая особенность БПФ, которая отсуствует в готовых ядрах FFT Xilinx.
Пример: требуется разработать узел БПФ, осуществляющий непрерывную работу входного потока комплексных чисел на частоте 800 МГц. Ядро от Xilinx такое не потянет (реальные тактовые частоты обработки в современных ПЛИС порядка 300–400 МГц), либо потребует каким-то образом децимировать входной поток. Кастомное ядро позволяет без предварительного вмешательства тактировать два входных отсчета на частоте 400 МГц вместо одного отсчета на 800 МГц. Другой минус ядра FFT Xilinx связан с невозможностью принимать входной поток в бит-реверсном порядке. В связи с чем тратится огромный ресурс памяти кристалла ПЛИС для перестановки данных в нормальный порядок. Для задач быстрой свертки сигналов, когда два узла БПФ стоят друг за другом, — это может стать критичным моментом, то есть задача просто не ляжет в выбранный кристалл ПЛИС. Кастомное ядро БПФ позволяет принимать на входе данные в нормальном порядке, а выдавать — в бит-реверсном, а ядро обратного БПФ — наоборот, получает данные в бит-реверсном порядке, а выдает в нормальном. Экономится сразу два буфера на перестановку данных!!!
Поскольку большая часть материала этой статьи могла пересекаться с предыдущей, я решил выкинуть все самое ненужное, сделав большой упор на математические операции в целочисленном формате на FPGA для реализации БПФ.
Параметры ядра БПФ
- NFFT — количество бабочек (длина БПФ),
- DATA_WIDTH — разрядность входных данных (4–32),
- TWDL_WIDTH — разрядность поворачивающих множителей (8–27).
- SERIES — задает семейство ПЛИС, на которой реализуется БПФ («NEW» — Ultrascale, «OLD» — 6/7 серия ПЛИС Xilinx).
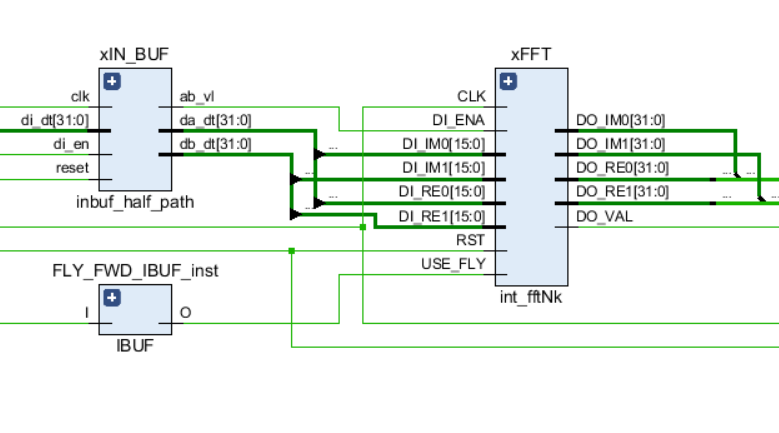
Как и любые другие звенья в цепи, БПФ имеет входные порты управления — тактовый сигнал и сброс, а также входные и выходные порты данных. Кроме того, в ядре используется сигнал USE_FLY, который позволяет динамически выключать бабочки БПФ для процессов отладки или возжности посмотреть исходный входной поток.
В таблице ниже приведен объем занимаемых ресурсов FPGA в зависимости от длины БПФ NFFT для DATA_WIDTH = 16 и двух разрядностей TWDL_WIDTH = 16 и 24 бит.

Ядро при NFFT = 64K стабильно работает на частоте обработки FREQ = 375 MHz на кристалле Kintex-7 (410T).
Структура проекта
Для удобства понимания особенностей тех или иных компонентов, приведу список файлов проекта и их краткое описание в иерархическом порядке:
- Ядра БПФ:
- int_fftNk — узел БПФ, схема Radix-2, децимация по частоте (DIF), входной поток — нормальный, выходной — бит-реверсный.
- int_ifftNk — узел ОБПФ, схема Radix-2, децимация по времени (DIT), входной поток — бит-реверсный, выходной — нормальный.
- Бабочки:
- int_dif2_fly — бабочка Radix-2, децимация по частоте,
- int_dit2_fly — бабочка Radix-2, децимация по времени,
- Комплексные умножители:
- int_cmult_dsp48 — общий конфигурируемый умножитель, включает в себя:
- int_cmult18×25_dsp48 — умножитель для небольших разрядностей данных и поворачивающих множителей,
- int_cmult_dbl18_dsp48 — удвоенный умножитель, разрядность поворачивающих множителей до 18 бит,
- int_cmult_dbl35_dsp48 — удвоенный умножитель, разрядность поворачивающих множителей до 25* бит,
- int_cmult_trpl18_dsp48 — утроенный умножитель, разрядность поворачивающих множителей до 18 бит,
- int_cmult_trpl52_dsp48 — утроенный умножитель, разрядность поворачивающих множителей до 25* бит,
- Умножители:
- mlt42×18_dsp48e1 — умножитель с разрядностями операндов до 42 и 18 бит на базе DSP48E1,
- mlt59×18_dsp48e1 — умножитель с разрядностями операндов до 59 и 18 бит на базе DSP48E1,
- mlt35×25_dsp48e1— умножитель с разрядностями операндов до 35 и 25 бит на базе DSP48E1,
- mlt52×25_dsp48e1— умножитель с разрядностями операндов до 52 и 25 бит на базе DSP48E1,
- mlt44×18_dsp48e2 — умножитель с разрядностями операндов до 44 и 18 бит на базе DSP48E2,
- mlt61×18_dsp48e2 — умножитель с разрядностями операндов до 61 и 18 бит на базе DSP48E2,
- mlt35×27_dsp48e2 — умножитель с разрядностями операндов до 35 и 27 бит на базе DSP48E2,
- mlt52×27_dsp48e2— умножитель с разрядностями операндов до 52 и 27 бит на базе DSP48E2.
- Сумматор:
- int_addsub_dsp48 — универсальный сумматор, разрядности операндов до 96 бит.
- Линии задержки:
- int_delay_line — базовая линия задержки, обеспечивает перестановку данных между бабочками,
- int_align_fft — выравнивание входных данных и поворачивающих множителей на входе бабочки БПФ,
- int_align_fft — выравнивание входных данных и поворачивающих множителей на входе бабочки ОБПФ,
- Поворачивающие множители:
- rom_twiddle_int — генератор поворачивающих множителей, с определенной длины БПФ считает коэффициенты на базе DSP ячеек ПЛИС,
- row_twiddle_tay — генератор поворачивающих множителей с помощью ряда Тейлора (NFFT > 2K)**.
- Буфер данных:
- inbuf_half_path — входной буфер, принимает поток в обычном режиме и выдает две последовательности отсчетов, сдвинутых на половину длины БПФ***,
- outbuf_half_path — выходной буфер, собирает две последовательности и выдает одну непрерывную равную длине БПФ,
- iobuf_flow_int2 — буфер работает в двух режимах: принимает поток в режиме Interleave-2 и выдает две последовательности сдвинутых на половину длины БПФ. Либо наоборот, в зависимости от опции «BITREV».
- int_bitrev_ord — простой преобразователь данных из натурального порядка в бит-реверсный.
* — для DSP48E1: 25 бит, для DSP48E2 — 27 бит.
** — с определенной стадии БПФ можно использовать фиксированное количество блочной памяти для хранения поворачивающих коэффициентов, а промежуточные коэффициенты высчитывать с помощью DSP48 узлов по формуле Тейлора до первой производной. В связи с тем, что для БПФ ресурс памяти важнее, можно смело жертвовать вычислительными блоками в угоду памяти.
*** — входной буфер и линии задержки — вносят существенный вклад в объем занимаемых ресурсов памяти ПЛИС
«Бабочка»
Все, кто хотя бы раз сталкивался с алгоритмом быстрого преобразования Фурье, знают, что в основе этого алгоритма лежит элементарная операция — «бабочка». Она преобразует входной поток, умножая входные данные на поворачивающие коэффициенты (twiddle factor). Для БПФ есть две классические схемы преобразования — децимация по частоте (DIF, decimation-in-frequency) и децимация по времени (DIT, decimation-in-time). Для DIT алгоритма характерно разбиение входной последовательности на две последовательности половинной длительности, а для DIF алгоритма — на две последовательности четных и нечетных отсчетов длительностью NFFT. Кроме того, эти алгоритмы отличаются математическими действиями для операции «бабочка».
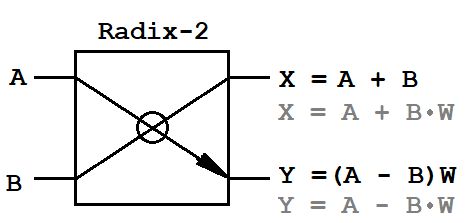
A, B — входные пары комплексных отсчетов,
X, Y — выходные пары комплексных отсчетов,
W — комплексные поворачивающие множители.
Поскольку входные данные — комплексные величины, то бабочка требует один комплексный умножитель (4 операции умножения и 2 операции сложения) и два комплексных сумматора (4 операции сложения). Это и есть весь математический базис, который необходимо реализовать на ПЛИС.
Умножитель
Следует отметить, что все математические операции на FPGA зачастую выполняются в дополнительном коде (2«s complement). Умножитель на ПЛИС можно реализовать двумя способами — на логике, используя триггеры и таблицы LUT, или на специальных блоках вычисления DSP48, которые давно и прочно вошли в состав всех современных ПЛИС. На логических блоках умножение реализуется с помощью алгоритма Бута или его модификаций, занимает достаточно приличный объем логических ресурсов и далеко не всегда удовлетворяет временным ограничениям на высоких частотах обработки данных. В связи с этим, умножители на ПЛИС в современных проектах практически всегда проектируются на базе DSP48 узлов и лишь изредка — на логике. Узел DSP48 — это сложная законченная ячейка, которая реализует математические и логические функции. Основные операции: умножение, сложение, вычитание, накопление, счетчик, логические операции (XOR, NAND, AND, OR, NOR), возведение в квадрат, сравнение чисел, сдвиг и т.д. На следующем рисунке представлена ячейка DSP48Е2 для семейства ПЛИС Xilinx Ultrascale+.

Путем нехитрой конфигурации входных портов, операций вычисления в узлах и выставления задержек внутри узла — можно сделать скоростную математическую молотилку данных.
Отметим, у всех топовых вендоров FPGA в среде проектирования есть стандартные и бесплатные IP-ядра для вычисления математических функций на базе узла DSP48. Они позволяют вычислять примитивные математичекие функции и выставлять различные задержки на входе и выходе узла. У Xilinx это IP-Core «multiplier» (ver. 12.0, 2018), которое позволяет конфигурировать умножитель на любую разрядность входных данных от 2 до 64 бит. Кроме того, можно задать способ реализации умножителя — на логических ресурсах или встроенных примитивах DSP48.
Оцените, сколько логики «кушает» умножитель с разрядностью входных данных на портах A и B = 64 бит. Если использовать узлы DSP48, то их потребуется всего 16.

Основное ограничение, накладываемое на ячейки DSP48 — разрядность входных данных. В узле DSP48E1, который является базовой ячейкой ПЛИС Xilinx 6 и 7 серии разрядность портов входа для умножения: «A» — 25 бит, «B» — 18 — бит, Следовательно, результат умножения представляет 43-битное число. Для семейства ПЛИС Xilinx Ultrascale и Ultrascale+ узел претерпел несколько изменений, в частности разрядность первого порта выросла на два бита: «A» — 27 бит, «B» — 18 — бит. Кроме того, сам узел называется DSP48E2.
Дабы не иметь привязку к конкретному семейству и кристаллу FPGA, обеспечить «чистоту исходного кода», и учесть все возможные разрядности входных данных, решено спроектировать собственный набор умножителей. Это позволит максимально эффективно реализовать комплексные умножители для «бабочек» БПФ, а именно — умножители и сумматор-вычитатель на базе DSP48 блоков. Первый вход умножителя — это входные данные, второй вход умножителя — поворачивающие множители (гармонический сигнал из памяти). Набор умножителей реализуется с помощью встроенной библиотеки UNISIM, из которой необходимо подключить примитивы DSP48E1 и DSP48E2 для дальнейшего их использования в проекте. Набор умножителей представлен в таблице. Следует отметить, что:
- Операция умножения чисел приводит к росту разрядности произведения как сумма разрядностей операндов.
- Каждый из умножителей 25×18 и 27×18 дублируются, по сути — это один компонент для разных семейств.
- Чем больше стадия параллельности операции — тем больше задержка на вычисление и больше объем занимаемых ресурсов.
- При меньшей разрядности на входе «B» можно реализовать умножители с бОльшей разрядностью на другом входе.
- Основное ограничение в наращивании разрядности вносит порт «B» (реальный порт примитива DSP48) и внутренний сдвиговый регистр на 17-бит.
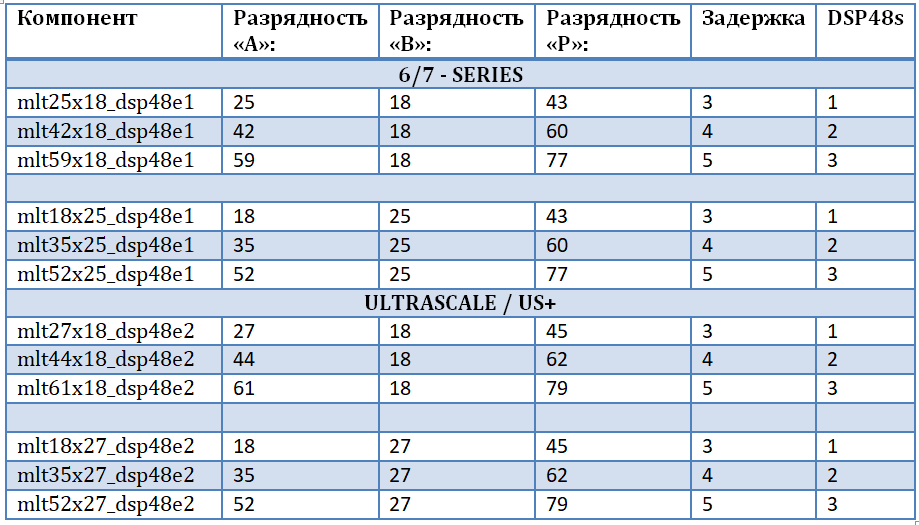
Дальнейшее увеличение разрядности не представляет интереса в рамках поставленной задачи по причинам, описанным ниже:
Разрядность поворачивающих множителей
Очевидно, что чем больше разрядность гармонического сигнала — тем точнее представляется число (больше знаков в дробной части). Но рзрядность порта B
Разрядность входных отсчетов
Разрядность данных типовых узлов приема и регистрации (АЦП, ЦАП) не велика — от 8 до 16 бит, и редко — 24 или 32 бита. Причем, в последнем случае эффективнее воспользоваться форматом данных с плавающей точкой по стандарту IEEE-754. С другой стороны, каждая стадия «бабочки» в БПФ прибавляет один разряд данных к выходным отсчетам из-за выполнения математических операций. Например, для длины NFFT = 1024 используется log2(NFFT) = 10 бабочек.
Следовательно, выходная разрядность будет на десять бит больше входной, WOUT = WIN + 10. В общем виде формула выглядит так:
WOUT = WIN + log2(NFFT);
Пример:
Разрядность входного потока WIN = 32 бит,
Разрядность поворачивающих множителей TWD = 27,
Разрядность порта «А» из списка реализованных умножителей в данной статье не превышает 52 бита. Это означает, что максимальное количество бабочек БПФ = 52–32 = 20. То есть возможно реализовать БПФ длиной до 2^20 = 1М отсчетов. (Однако, на практике, прямыми средствами такое невозможно в связи с ограниченностью ресурсов даже у самых мощных кристаллов ПЛИС, но это относится к другой теме и в статье рассматриваться не будет).
Как видно, это одна из главных причин, по которой я не стал реализовывать умножители с бОльшей разрядностью входных портов. Используемые умножители покрывают полный диапазон требуемых значений разрядности входных данных и поворачивающих множителей для задачи вычисления целочисленного БПФ. Во всех остальных случаях можно воспользоваться вычислением БПФ в формате с плавающей точкой!
Реализация «широкого» умножителя
На базе простого примера умножения двух чисел, не вписывающихся в разрядность стандартного узла DSP48, я покажу, как можно реализовать широкий умножитель данных. На следующем рисунке представлена его структурная схема. Умножитель реализует перемножение двух знаковых чисел в дополнительном коде, разрядность первого операнда X — 42 бита, второго Y — 18 бит. Она содержит два узла DSP48E2. Для выравнивания задержек в верхнем узле используется два регистра. Это сделано по той причине, что в верхнем сумматоре нужно правильно сложить числа из верхнего и нижнего узлов DSP48. Нижний сумматор фактически не используется. На выходе нижнего узла стоит дополнительная задержка произведения для выравнивания выходного числа по времени. Суммарная задержка — 4 такта.

Произведение складывается из двух компонент:
- Младшая часть: P1 = »0» & X[16:0] * Y[17:0];
- Старшая часть: P2 = X[42:17] * Y[17:0] + (P1 >> 17);
Сумматор
Аналогично умножителю, сумматор может строиться на логических ресурсах, используя цепочку переноса, или на DSP48 блоках. Для достижения максимальной пропускной способности второй метод предпочтительнее. Один примитив DSP48 позволяет реализовать операцию сложения до 48 бит, два узла — до 96 бит. Для реализуемой задачи таких разрядностей вполне достаточно. Кроме того, примитив DSP48 обладает специальным режимом «SIMD MODE», который распараллеливает встроенный 48-битный АЛУ на несколько операций с разными данными небольшой разрядности. То есть, в режиме «ONE» используется полная разрядная сетка в 48 бит и два операнда, а в режиме «TWO» разрядная сетка разбивается на несколько параллельных потоков по 24 бита каждый (4 операнда). Этот режим, используя всего один сумматор, помогает сократить количество занимаемых ресурсов кристалла ПЛИС на небольших разрядностях входных отсчетов (на первых стадиях вычисления).
Рост разрядности данных
Операция умножения двух чисел с разрядностями N и M в двоичном дополнительном коде приводит к росту выходной разрядности до Р = N + M.
Пример: для перемножения трехбитовых чисел N = M = 3, максимальное положительное число равно +3 = (011)2, а максимально отрицательное число — 4 = (100)2. Старший бит отвечает за знак числа. Следовательно, максимально возможное число при умножении — это +16 = (010000)2, которое образуется в результате умножения двух максимально отрицательных чисел -4. Разрядность выходных данных равна сумме входных разрядностей Р = N+M = 6 бит.
Операция сложения двух чисел с разрядностями N и M в двоичном дополнительном коде приводит к росту выходной разрядности на один бит.
Пример: сложим два положительных числа, N = M = 3, максимальное положительное число равно 3 = (011)2, а максимальное отрицательное число — 4 = (100)2. Старший бит отвечает за знак числа. Следовательно, максимальное положительное число — это 6 = (0110)2, а максимальное отрицательное число — это -8 = (1000)2. Разрядность выходных данных увеличивается на один бит.
Учет особенностей алгоритма
Усечение разрядности сверху:
Для минимизации ресурсов ПЛИС в алгоритме БПФ решено при умножении данных в бабочке никогда не использовать максимально возможное отрицательное число для поворачивающих коэффициентов. Эта поправка не вносит никакого негативного влияния в результат. Например, при ипсользовании 16-битного представления поворачивающих множителей минимальное число -32768 = 0×8000, а следующее за ним -32767 = 0×8001. Погрешность при замене максимально отрицательного числа на ближайшее соседнее значение составит ~0.003% и полностью приемлимо для реализации задачи.
Убрав в произведении двух чисел минимальное число, на каждой итерации можно сократить один неиспользуемый старший разряд. Пример: данные — 4 = (100)2, коэффициент +3 = (011)2. Результат умножения = -12 = (110100)2. Пятый бит можно отбросить, т.к. он дублирует соседний, четвертый — знаковый бит.
Усечение разрядности снизу:
Очевидно, что умножая в «бабочке» входной сигнал на гармоническое воздействие, не требуется тянуть выходную разрядность в следующие бабочки, а требуется округление или усечение. Поворачивающие множители представлены в удобном M-битном формате, однако на деле это обычный синус и косинус, нормированные к единице. То есть число 0×8000 = -1, а число 0×7FFF = +1. Следовательно, результат умножения обязательно усекается до исходной разрядности данных (то есть M бит от поворачивающих множителей усекаются снизу). Во всех реализациях БПФ, что мне довелось видеть, поворачивающие множители нормированы к 1 теми или иными способами. Следовательно, из результата умножения необходимо взять биты в следующей сетке [N+M-1–1: M-1]. Старший бит не используется (вычетаем дополнительную 1), младшие — усекаются.
Сложение/вычитание данных в операциях «бабочки» никак не подвергается минимизации и только эта операция вносит вклад в рост разрядности выходных данных на один бит на каждой стадии вычисления.
Отметим, что на первой стадии алгоритма FFT DIT или на последней стадии алгоритма FFT DIF данные необходимо умножить на поворачивающий множитель с нулевым индексом W0 = {Re, Im} = {1, 0}. В связи с тем, что умножение на единицу и ноль — примитивные операции, их можно не исполнять. В таком случае операция комплексного умножения вообще не требуется: вещественная и мнимая компоненты проходят «поворот» без изменений. На второй стадии используется два коэффициента: W0 = {Re, Im} = {1, 0} и W1 = {Re, Im} = {0, -1}. Аналогично, операции можно свести к элементарным преобразованиям и использовать мультплексор для выбора выходного отсчета. Это позволяет существенно сэкономить DSP48 блоки на первых двух бабочках.
Комплексный умножитель строится аналогично — на базе умножителей и сумматора-вычитателя, однако для некоторых вариантов разрядности входных данных дополнительные ресурсы не потребуются, о чем будет рассказано ниже.
Входной буфер и линии задержки и кросс-коммутаторы аналогичны тем, что описаны в предыдущей статье. Поворачивающие множители стали целочисленными с конфигурируемой разрядностью. В остальном — глобальных изменений в проектировании ядра БПФ — нет.
Особенности ядра БПФ INT_FFTK
- Полностью конвейерная схема обработки данных.
- Длина преобразования NFFT = 8–512K точек.
- Гибкая настройка длины преобразования NFFT.
- Целочисленный формат входных данных, разрядность конфигурируется.
- Целочисленный формат поворачивающих множителей, разрядность конфигурируется.
- Компактное хранение поворачивающих коэффициентов через разложение в ряд Тейлора до первой производной.
- Рост разрядности на каждой стадии вычисления и на выходе ядра!
- Хранение четверти периода коэффициентов для экономии ресурсов кристалла.
- БПФ: данные на входе — в прямом порядке, на выходе в двоично-инверсном.
- ОБПФ: данные на входе в двоично-инверсном порядке, на выходе — в прямом.
- Конвейерная схема обработки с двухкратным параллелизмом. Radix-2.
- Минимальная неразрывная длина пачки данных равна NFFT отсчетов*.
- Высокая скорость вычислений и небольшой объем занимаемых ресурсов.
- Реализация на последних кристаллах ПЛИС (Virtex-6, 7-Series, Ultrascale).
- Частота работы ядра ~375MHz на Kintex-7
- Язык описания — VHDL.
- Отсутствие необходимости операции преобразования bitreverse для связки БПФ+ОБПФ.
- Open Source проект без включения сторонних IP-Cores.
Исходный код
Исходный код ядра БПФ INTFFTK на VHDL (включая базовые операции и набор умножителей) и m-скрипты для Matlab / Octave доступны в моем профиле на гитхабе.
Заключение
В ходе разработки спроектировано новое ядро БПФ, обеспечивающее высокую производительность по сравнению с аналогами. Связка ядер БПФ и ОБПФ не требует перевода в натуральный порядок, а максимальная длина преобразования ограничена лишь ресурсами ПЛИС. Двукратный параллелизм позволяет обрабатывать входные потоки удвоенной частоты, чего не может делать IP-CORE Xilinx. Разрядность на выходе целочисленого БПФ линейно растет в зависимости от количества стадий преобразовани.
В прошлой статье я писал о дальнейших планах: ядра БПФ Radix-4, Radix-8, Ultra-Long FFT на много миллионов точек, FFT-FP32 (в формате IEEE-754). Если коротко, то они практически все разрешены, но по тем или иным причинам в настоящий момент не могут быть вынесены на публику. Исключение составляет алгоритм FFT Radix-8, к которому я даже не присупал (сложно и лень).
Не уверен, буду ли я заниматься цифровой обработкой на ПЛИС в будущем, но если я останусь в рядах разработчиков и радиоинженеров, то вскоре вы увидите и другие интересные проекты с открытым исходным кодом! В очередной раз выражаю благодарность dsmv2014, который всегда приветствовал мои авантюрные идеи. Спасибо за внимание!
