Разжёвываем линейно-квадратичный регулятор для управления перевёрнутым маятником
Продолжаю подробное описание использования линейно-квадратичного регулятора на примере управления перевёрнутым маятником. К слову сказать, термин «ЛКР» очень неточно отражает суть происходящего, как мне уже подсказали в комментариях, в русской школе теории управления этот подход называется «аналитическим конструированием регуляторов», что существенно точнее.
Как обычно, я стараюсь разжевать математику по-максимуму, чтобы материал был доступен заинтересованному школьнику. Я глубоко убеждён, что использование математики по-хорошему должно бы быть платным: любая формула должна быть использована только тогда, когда она призвана облегчить понимание, а не для того, чтобы выпендриваться.
Итак, это уже четвёртая статья, для лучшего понимания происходящего неплохо бы прочитать предыдущие три:
Вот фотография системы (кликабельно):

У меня только два источника информации о происходящем в системе, это два инкрементальных энкодера, один (1000 импульсов на оборот) показывает положение каретки, второй (2000 импульсов на оборот) даёт положение самого маятника. В предыдущей статье я считал импульсы при помощи самой же ардуины, но это довольно неточно и слабо устойчиво к зашумлённым показаниям энкодеров. Кроме того, это тратит и без того слабые вычислительные ресурсы атмеги. Сейчас я поставил одну микросхему HCTL-2032 (примерно пять евро штука на алиэкспрессе), она умеет считать импульсы двух энкодеров, предоставляя для этого 32-битные счётчики. Чтобы сэкономить ноги ардуины, между счётчиком и самой ардуиной стоит 74hc165, читающая один байт в параллель и отдающая этот байт последовательно.
По сравнению с прошлой статьёй у меня чуточку изменились параметры системы (другой драйвер двигателя плюс поставил энкодер на каретку), поэтому измеряю ещё раз параметры системы. Итак, с небольшим шагом (примерно в один вольт, от -24В до 24В) подаю постоянное напряжение на двигатель и измеряю изменение скорости каретки. Скорость каретки считается как разность между соседними положениями каретки делить на прошедшее время (о корректности такого подхода позже). Использовавшийся код можно увидеть здесь.
По горизонтали время в секундах, а по вертикали скорость движения каретки в метрах в секунду. Зашумлённые кривые — это результаты реального измерения, гладкие — это моя математическая модель системы. На сейчас задача посчитать именно модель для гладких кривых, приближающих реальность.

Выяснилось, что я слегка перестарался с мотором, на 24В каретка ускоряется примерно на 60 метров в секунду за секунду и жёсткости системы не хватает для разумного измерения чего бы то ни было. Поэтому обрезаю измерения на пятнадцати вольтах, в начальной части кривых можно видеть колебания в скорости каретки.
Итак, для каждого измерения считаю установившуюся скорость (высота плато) и рисую график, на котором по горизонтали поданное напряжение, а по вертикали установившаяся скорость.
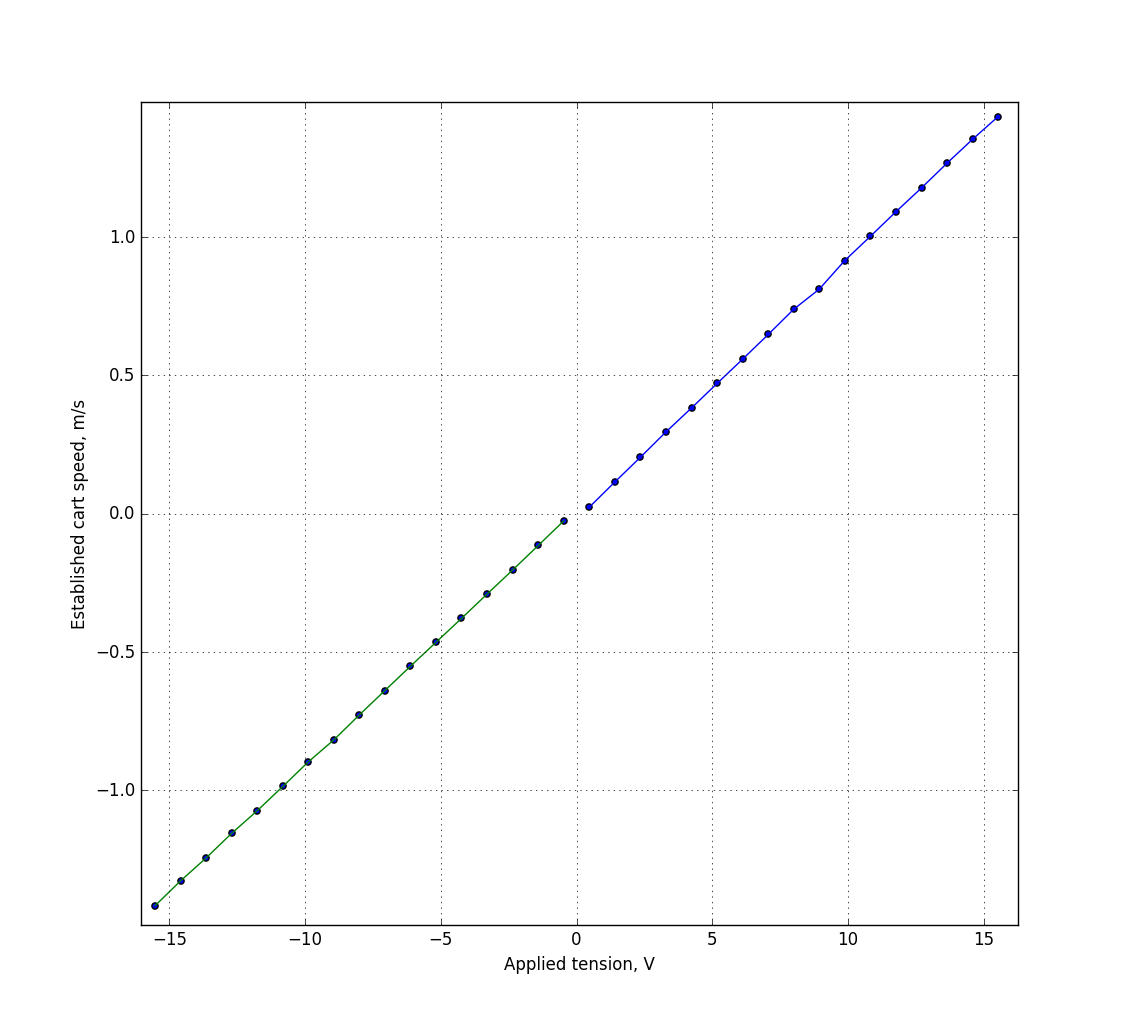
Если бы у меня в системе не было бы трения, то этот график был бы линейным, и моя модель строилась бы как v_{k+1} = a*v_k + b*u_k. И ведь он практически линеен на своей положительной и отрицательной частях одновременно, но эти две прямые не проходят через ноль. Это (в том числе) из-за трения. Мы видим, что если при положительном напряжении мы добавим, а при отрицательном отнимем буквально долю вольта, то график пройдёт через ноль и станет линейным.
Если мы хотим учитывать трение в системе, то модель строится следующим образом (не забудьте прочитать предыдущую статью, если неясно, откуда берётся эта формула):
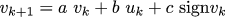
Итак, имея данные, нам нужно найти значения a, b и c. Фиттинг можно делать как угодно, учитывая, что он делается только один раз на десктопе, можно просто сделать три вложенных цикла. Вот код фиттинга, который мне говорит, что для дискретизации в 20 мс между измерениями a=.4, b = .06, c=-.01. То есть, напряжение, необходимое для компенсации трения у меня в системе, равно одной десятой вольта. Кривые, полученные таким приближением, наложены на реальное измерение на картинке выше.
Итого, на данный момент наша система может быть записана следующим образом:
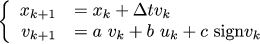
К сожалению, это не является линейным дифференциальным уравнением вида x_{k+1} = A x_k + B u_k, которое нужно для линейно-квадратичного регулятора. Кроме того, даже если бы не это, то мне нужно добавить ещё и маятник на каретку, а я не знаю как вывести зависимость положения и угловой скорости маятника от напряжения. Я бы предпочёл, чтобы у меня в качестве управления было бы не напряжение, а непосредственно ускорение каретки:

Окей, предположим, что мой регулятор использует ускорение в качестве управления. Но ведь в реальности-то я должен подать напряжение на мотор. Как его получить? Очень просто:

То есть, имея текущую скорость (состояние системы), мы легко можем посчитать напряжение, которое нужно приложить, чтобы получить необходимое ускорение. Таким образом, мы убили двух зайцев разом: и избавились от нелинейности в регуляторе, но при это оставив компенсацию трения, и получили интуитивно понятный контроль. Мне куда как проще представлять себе ускорение, нежели напряжение, которое очень нелинейно влияет на скорость.
Уравнения движения маятника
Итак, задача добавить маятник в нашу систему и записать соответствующие линейные уравнения для регулятора. Давайте приведём полный список необходимых для этого физических величин:
- m: масса маятника
- M: масса каретки
- f: сила, приложенная мотором к каретке через ремень
- 2l: длина маятника (l — это расстояние от петли до центра масс маятника)
- I: момент инерции маятника (к слову, а ваши шрифты позволяют видеть разницу между I и l?)
- θ (t): угол отклонения маятника от вертикали, в положении неустойчивого равновесия нулевой, увеличивается по часовой стрелке
- x (t): положение каретки
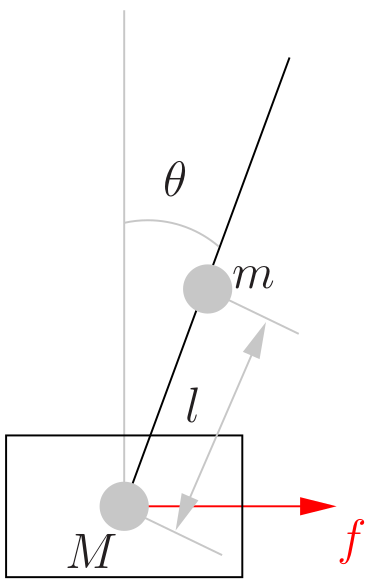
Итого, переменными моей системы будет четырёхмерный вектор, состоящий из положения каретки, её скорости, угла отклонения маятника и его угловой скорости. Задача на сейчас записать систему линейных дифференциальных уравнений вот такого вида:
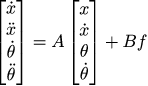
Если мы сумеем её записать в непрерывном виде, то потом просто дискретизуем и мы выиграли бой. Обратите внимание, что тут я использую в качестве управления приложенную силу, а не ускорение, но второй закон Ньютона нам покажет, как это сделать. Итак, нам нужно найти неизвестные матрицы A и B.
Запишем второй закон Ньютона для каретки: ускорение каретки, помноженное на массу, равняется сумме двух горизонтальных сил: первая сила — это наше управление, сила, приложенная через ремень электромотором. Вторая сила — это сила, с которой маятник, стараясь упасть или подняться, толкает каретку вбок. Чтобы её найти, можно записать координаты центра массс маятника как двумерный вектор (x (t) + l sin (θ (t)), l cos (θ (t))). Если мы продифференцируем дважды координату, то получим ускорение, а сила — это ускорение на массу. Поскольку нас интересует только горизонтальная составляющая, то имеет смысл брать только вторую производную от x (t) + l sin (θ (t). Итого:
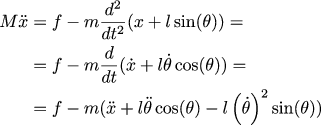
Это нелинейное уравнение, но оно может быть хорошо приближено линейным вокруг точки равновесия. Если угол близок к нулевому, то первый замечательный предел (ну или ряд Тейлора) говорят, что синус угла примерно равен углу. То же самое для косинуса: для углов, близких к нулевым, косинус почти равен единице. Ну и точно так же пренебрежём степенями, начиная с квадрата (если у нас скорость равна .1 радиана в секунду, то квадрат скорости даст совсем маленький вкла, поэтому пренебрегаем им смело):
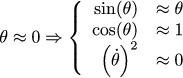
Тогда предыдущее уравнение может быть приближено линейным:

Теперь запишем второй закон Ньютона (версия для вращения) для маятника. Для начала, что такое второй закон Ньютона для вращения? Это сумма моментов равна угловому ускорению, помноженному на момент инерции. Момент инерции — это такой аналог массы для поступательного движения. Нас интересует проекция всех сил на прямую, перпендикулярную маятнику (ведь вращает только перпендикулярная составляющая, правда?) Ну и разумеется, эти силы надо помножить на плечо, чтобы получить момент. Сил, действующих на маятник, три: гравитация и горизонтальная и вертикальная составляющие силы реакции опоры, которые мы можем получить как и в прошлый раз, дважды взяв производную по времени от координат центра масс маятника:
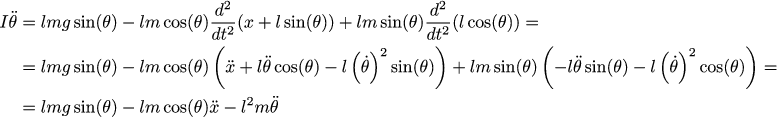
Приблизим его линейным уравнением:

Запишем уравнения (1) и (2) в систему:
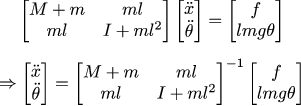
Для удобства назовём определитель матрицы буквой D:

Обратим матрицу:

Теперь запишем наши дифференциальные уравнения, по факту, мы нашли матрицы A и B:

Дискретизируем линейную систему
Итак, мы записали неперывное дифференциальное уравнение:

Для постоянного шага Δt получаем следующее:

Если мы обозначим через E единичную матрицу 4×4, то можно записать:

Момент инерции для стержня, который вращается вокруг конца, можно посмотреть здесь, поэтому упрощаем всё что можно:

Это и есть самое главное уравнение движения маятника.
Код вычисления коэффициентов регулятора можно взять здесь. Раньше я использовал наименьшие квадраты для подсчёта, но это всё же довольно громоздко, поэтому в новом коде матрица усиления считается напрямую.
Итак, ЛКР нам говорит, что если взять управляющую силу f_k = 24.95 x_k + 18.54 v_k + 70.44 θ_k + 14.96 ω_k, то отклонив маятник на 12° от вертикали, и уведя каретку на 20 сантиметров от положения рановесия, то мы должны получить следующее поведение системы:
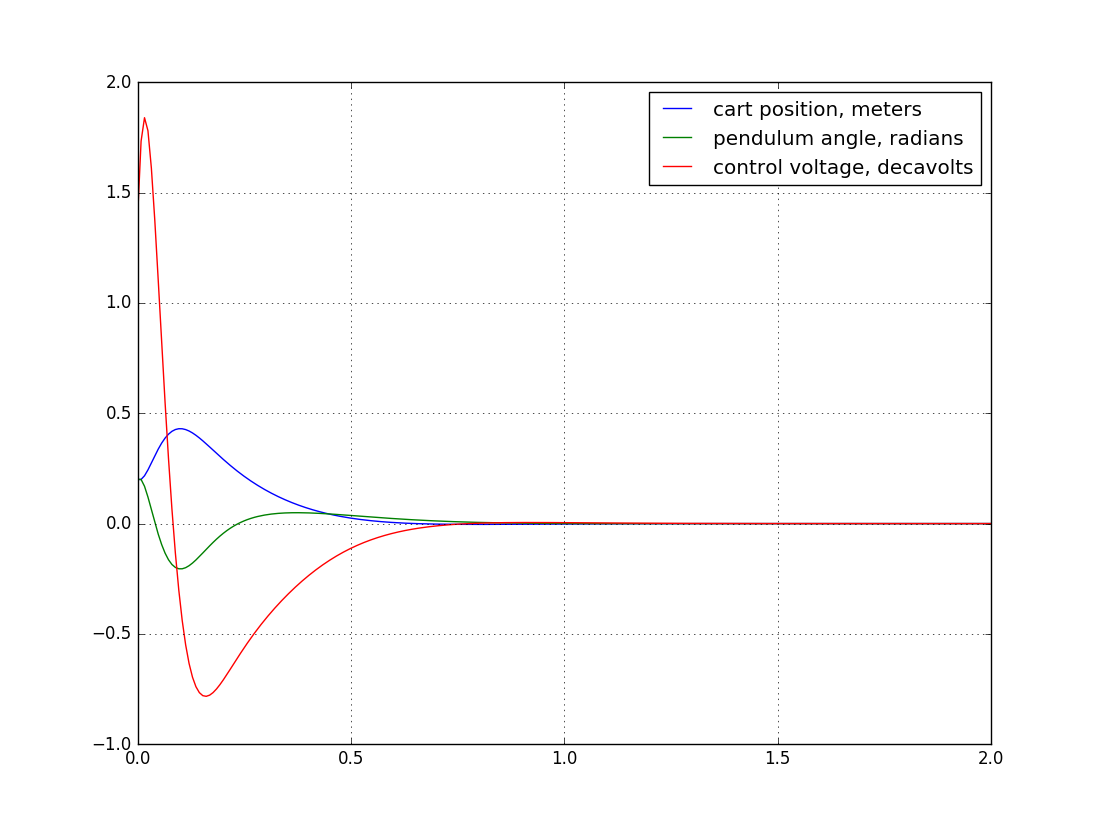
x_k — положение каретки, v_k — её скорость, θ_k — угол маятника, ω_k — его угловая скорость. Напряжение на графике дано в десятках вольт, чтобы примерно сравнять масштабы трёх графиков.
Вот таким у меня получился маятник, управляющий код можно посмотреть здесь:
В принципе, результатом я пока вполне доволен. Амплитуда отклонения каретки от желаемого положения в районе двух сантиметров, что довольно прилично. Почему она не стоит как вкопанная на нулевой позиции, ловя отклонения маятника очень маленькими движениями? Причин несколько. Самая простая — люфт в редукторе мотора, который составляет примерно пять миллиметров положения каретки, что означает, что каретке довольно дорого менять направление движения. Следующая, и не менее важная причина — это оценка угловой скорости движения маятника (ну и скорости движения каретки).
Как оценить скорость движения, если в наличии лишь инкрементальный энкодер? Самый простой способ — это взять два последних значения энкодера и поделить их разницу на прошедшее время.Это известно как конечные разности и довольно широко применяется на практике.
Давайте посмотрим на следующий график:
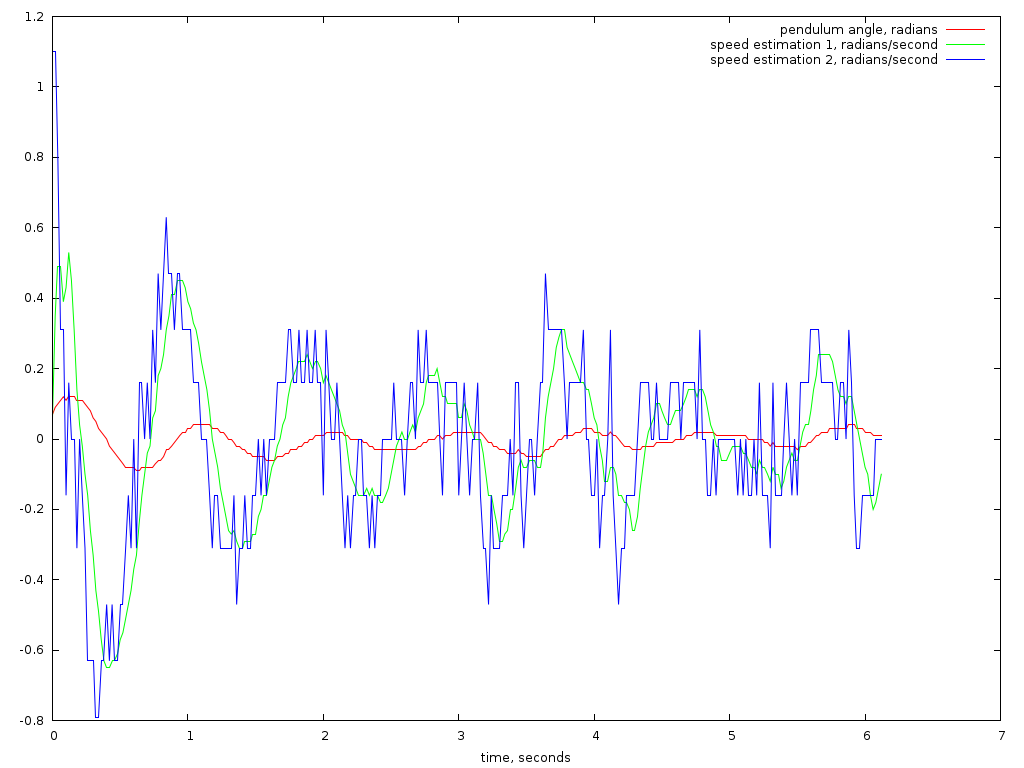
Я записал угол маятника в течение нескольких секунд, он показан красным. График слегка зашумлён из-за разрешения энкодера, но в общем и целом довольно гладкий. Скорость нам приходится находить синтетически из истории положения маятника. Если мы возьмём напрямую разность двух соседних положения и поделим на 20 миллисекунд, то это нам даст синий график. Польза конечных разностей в том, что они очень просто программируются. Их недостаток в том, что они драматическим образом усиливают любой шум измерений.
Если взять такую оценку скорости, то регулятор сходит с ума:
Единственная разница с предыдущим видео — это оценка скорости, ничего больше.
По-хорошему, нужно бы приблизить красную кривую каким-нибудь многочленом, и считать его производную, это основная идея фильтра Савицкого-Голея. Чтобы не ломать голову, я просто сгладил оценку скорости, взяв не соседние сэмплы, а разницу текущего сэмпла и восемь сэмплов тому назад, поделив на (20 мс*8). Такой подход сильно сглаживает оценку скорости, но его недостаток в том, что он вносит лаг в систему. Посмотрите на зелёную кривую: она явно отстаёт от реального положения вещей. Такая задержка в оценке и заставляет мой маятник слегка покачиваться.
К слову сказать, если взять фильтр Савицкого-Голея в лоб, то он тоже создаст похожую задержку. Таким образом, я нашёл разумный для меня компромисс между достижением цели и простотой артиллерии. Бороться с зашумлёнными измерениями я планирую совсем другими методами, это тема для последущих разговоров. Также в последующие разговоры будет входить автоматическая раскачка маятника, чтобы он сам поднимался из нижнего состояния в верхнее.
Stay tuned!
