Разработка системы мнемонического запоминания чисел
Я довольно давно поставил себе цель научиться запоминать числа, в основном просто как задача для саморазвития, очевидной практической выгоды не нашел. Однако хочется запоминать телефонные номера, маршруты транспорта, даты. Мне было трудно найти и начать пользоваться готовым решением, зато захотелось поработать над своим.
- Предпосылки
- Как проверить, хороша ли система?
- Проверяем несколько систем
- Как создать систему лучше
- Ссылка на репозиторий и послесловие
- Мнемоника — это способ запоминания с помощью цепочек ассоциаций. Удобнее всего запоминать цепочки слов, представляя себе каждое слово в виде образа и увязывая их вместе. Мозг легче запоминает такую графически-пространственную информацию. Например, можно запоминать ключевые слова из каждого тезиса к докладу. При этом важно верно выбирать образы, они должны быть одного порядка и не слишком абстрактными, иначе их взаимодействие не будет таким красочным и запомнить будет сложно.
- Для запоминания чисел используют кодирование цифр буквами — каждой цифре ставится в соответствие несколько гласных букв, обычно от 1 до 3. Двух- и трех- значные числа кодируются одним словом из, соответственно, двух и трех слогов. Или, если точнее, двух или трех вхождений гласных, слог может быть и один. Например, если 1 — это Д, 2 — это П, то 11 это дед, 12 это депо, а 22 это просто попа.
- Таким образом, для быстрого запоминания чисел необходимо знать наизусть какому числу какие буквы соответствуют и придумывать слова, увязывать их в цепочки.
- На практике, придумывать каждый раз слова медленно, поэтому нужно выучить 100 слов для чисел от 0 до 99. Профессионалы иногда знают слова до чисел до 999.
- При этом почему-то те мнемонические системы, которые я нашел, используют такие соответствия, что придумать слова сложно, запомнить тоже не очень. Они используют буквы, похожие на цифры по звучанию или написанию, чтобы было легче запомнить соответствие. Хотя легче не становится, т.к. 1–2 цифры такие не похожи, а вариантов «похожести» много.
- Отдельно отмечу, что использовать мнемоническую систему на английском языке я не взялся, ибо мне показалось, что знания языка не хватит, всё-таки думать быстро на нем не могу.
- Таким образом, встает вопрос, можно ли выбрать более удобные соответствия? Для выбора планировалось использовать полный перебор или методы машинного обучения.
Поскольку основным недостатком найденных систем я считаю сложность составления слов для некоторых чисел, то хотелось бы считать именно количество слов.
Вместо того, чтобы использовать какую-либо книгу, я использовал готовый частотный словарь. Словарь основан на национальном корпусе русского языка, который, в свою очередь, включает анализ многих книг, стихотворений разных жанров.
Частотный словарь доступен в виде csv-файла, который я решил проанализировать. Ниже скриншоты из Jupyter Notebook, для желающих в конце статьи имеется ссылка на github.
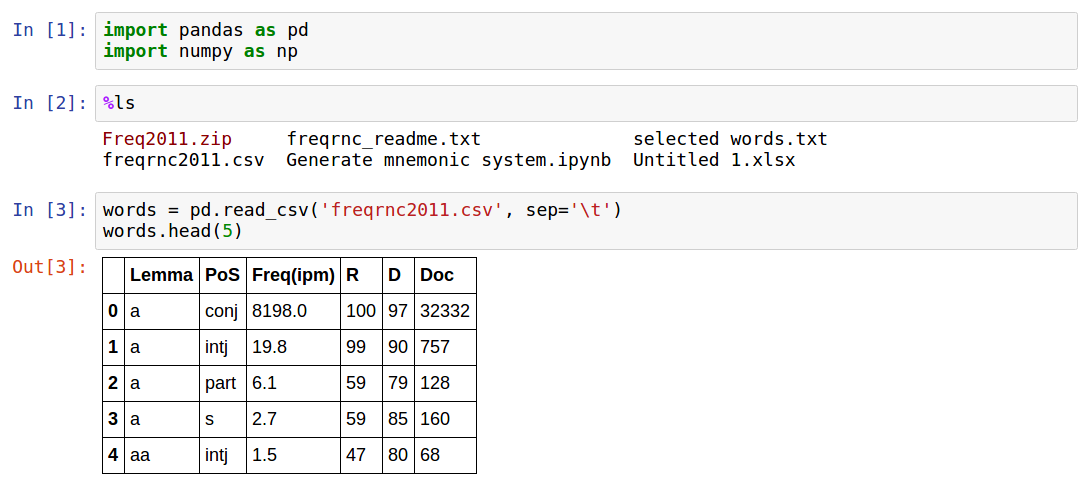
Как видно, данные содержат:
- само слово (лемму)
- обозначение части речи
- четыре метрики частоты, описанные во введнии к словарю
Я выбрал одну меритку часоты, поскольку мне важно только ранжирование. Методом проб и ошибок оказалось, что существительные — это «s».
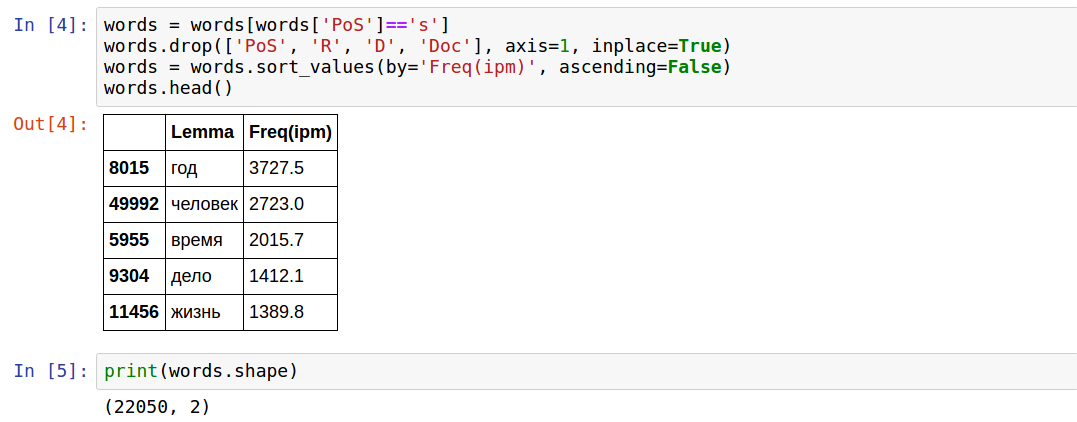
Таким образом, осталось два столбца и 22050 слов.
Однако среди этих слов есть много, которых я не знаю. Кроме того, я не хочу, чтобы основными в коде были «редкие» буквы, поэтому я решил отобрать слова, в которых таких редких букв нет. Как позже оказалось, идея не очень рабочая, но тем не менее.
Выбрав «простые» и «сложные» буквы, посчитаем их количество. Кроме того, выведем общее количество согласных букв в слове.
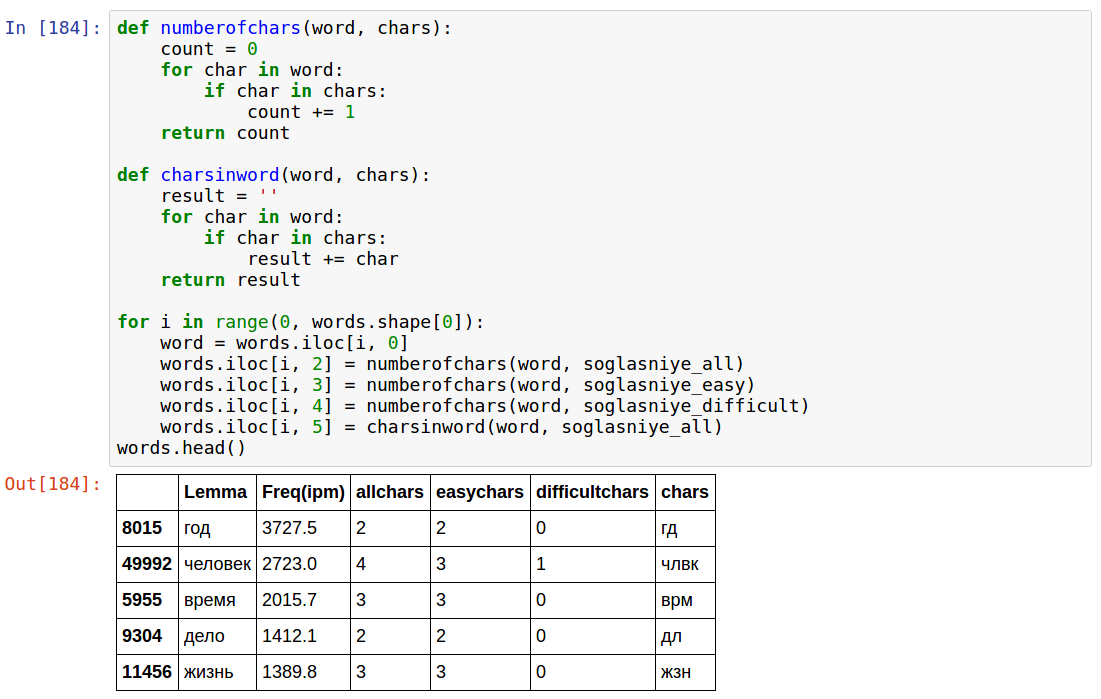
Отметим:
- allchars соответствует количеству цифр, которые можно зашифровать этим словом
- chars — это то, что можно напрямую соотнести с числом, если иметь соответствующее соответствие (я специально)
- этот код — единственный в данной статье, который работает не «моментально», а занимает около 10 секунд; я не стал думать, как сделать быстрее
Далее я подумал, что нужно отобрать слова с 2–3 согласными, без «сложных» букв, а также выбрать те, которые я знаю. Можно отрезать по своему усмотрению список отсортированный по частоте. Как позже я узнал, это идея тоже не очень, т.к. распределение слов неравномерное: всё-таки среди редких слов много известных.
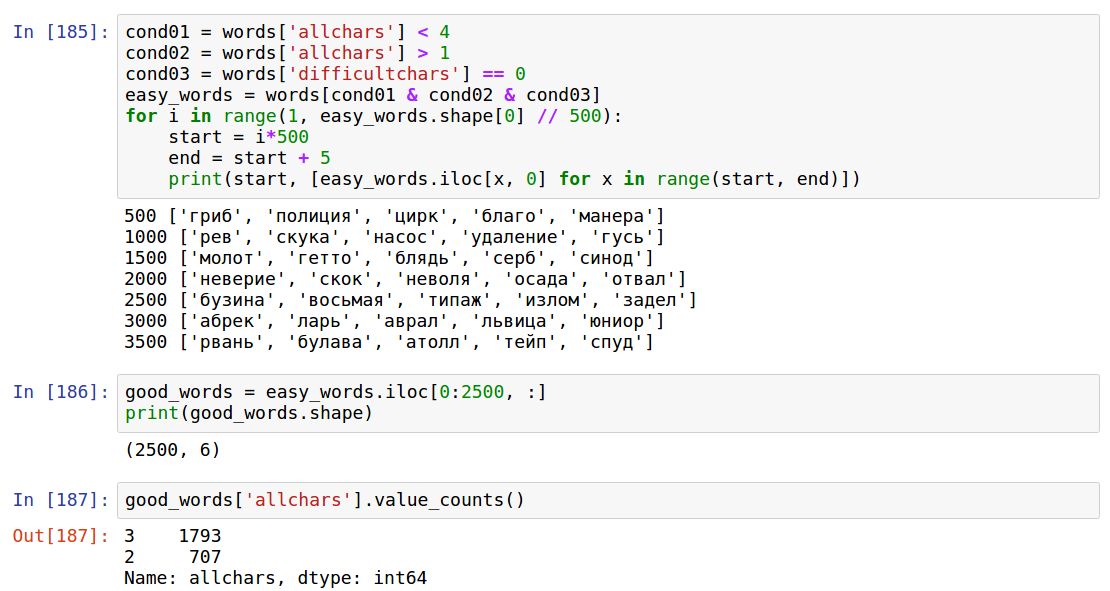
Так или иначе, в «хорошие» слова попало 2500 слов, поскольку я не знаю, что такое тейп и спуд. Из них 707 слов кодировали числа от 10 до 99 и 1793 числа от 100 до 999. Тут надо отметить, что 707 слов — это не так уж много для 90 чисел, меньше 10 слов на число, и это вместе с абстрактными и неизвестными.
Далее я задал следующие функции:
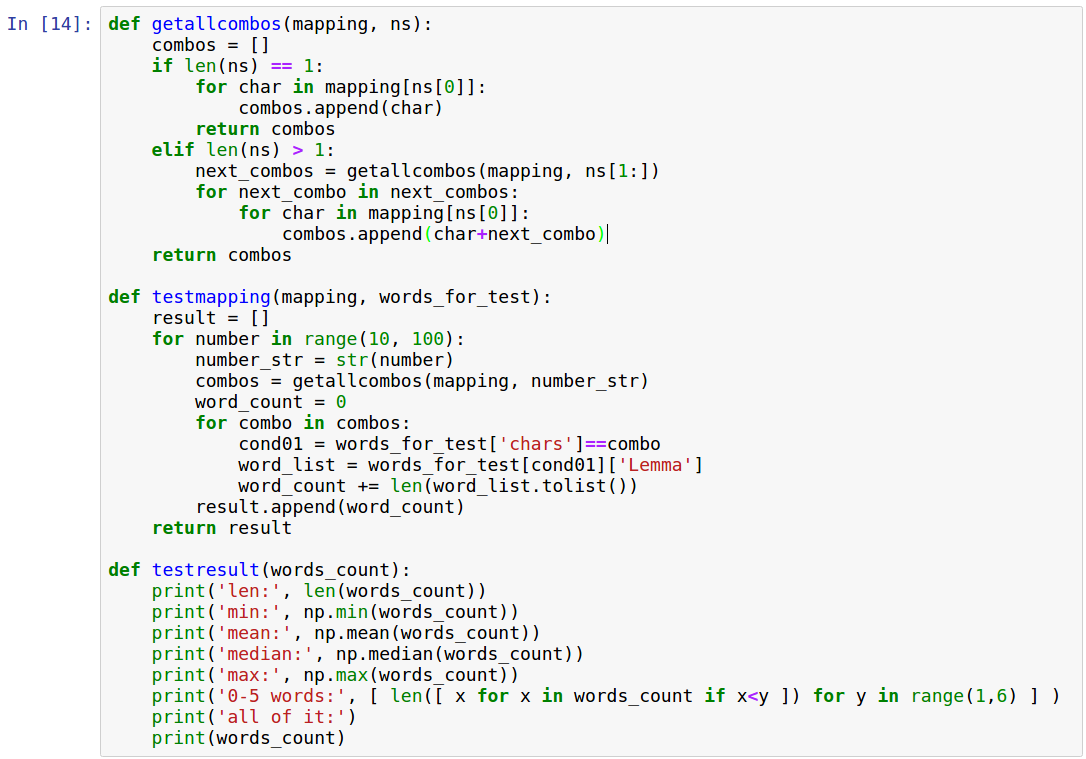
- getallcombos рекусрисвно считает все комбинации, которыми с помощью mapping (словарь число: буквы) можно закодировать число (ns — число в виде строки); возвращает список комбинаций
- testmaping проверяет сколькими словами из words_for_test (DataFrame с нашими столбцами, включая chars — только согласные) можно закодировать числа от 10 до 100 согласно предоставленному mapping; возварщает список с количеством слов для каждого числа
- testresult печатает некоторые статистики; учитывая опыт при подготовке, я для статьи оставил только строку с »0–5 words», которая показывает, сколько чисел удалось закодировать 0 словами, сколько лишь 1 словом и т.д.
Таким образом, для проверки любого мэппинга достаточно его задать и вызвать функцию тестирования.
Первой мне попалась система Джордано. На ней основаны многие мобильые приложения для обучения мнемонике, она упоминается и в интернете, см., например, тут.
Именно она мне показалась сложной в работе. Попробуйте, например, придумать слова для 84 или 11. Отмечу, что в приложениях есть уже готовые образы для чисел, но тогда нужно запомнить именно их, сто штук. В этом случае есть еще вариант запомнить какие-то свои, себе близкие образы.
Так или иначе, результаты теста такие:
Результаты по всем словам трудно сходу проинтерпретировать, а для «простых» слов видно, что для 22 чисел вообще нет ни одного слова.
Другой мэппинг, основанный на том, с какой буквы начинается название цифры, приводится на одном сайте саморазвития. Проверим:
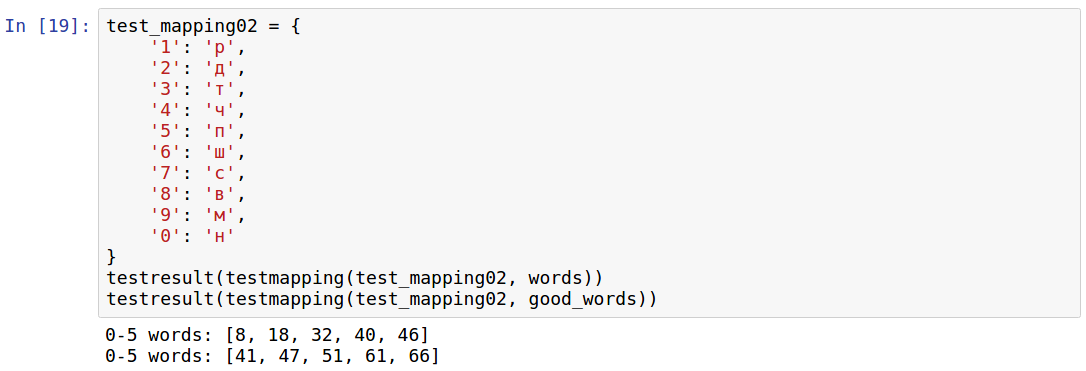
Как видно, стало сильно хуже, для 8 цифр вообще нет слов. Отмечу, что например мало слов где есть только две согласных буквы Р. Но и тем более плохая идея использовать для кода только редкие буквы вроде Ш и Ч.
В процессе подбора системы получше были следующие этапы:
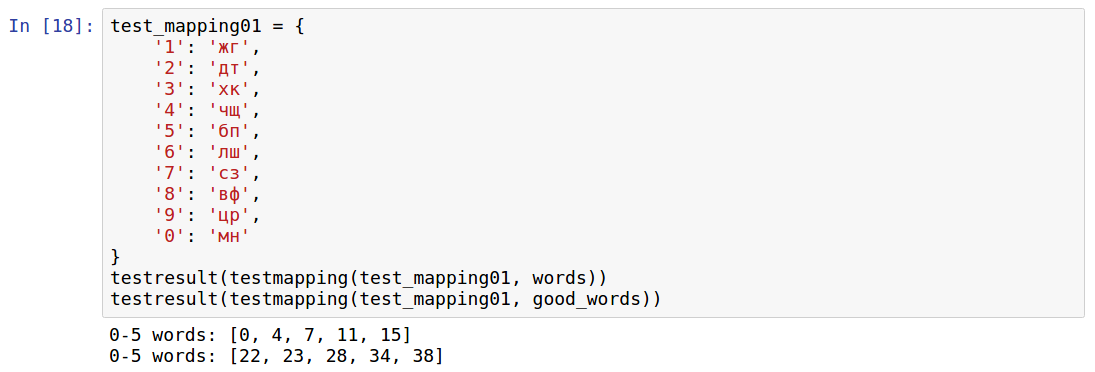
- [0, 4, 7, 11, 15] Наш бейзлайн из системы джордано
- Подумать над алгоритмом перебора или машинного обучения. Я не придумал и решил, что лучше подгонять на основе частоты встречаемости букв.
- [4, 8, 11, 15, 19] Сначала я взял все популярные буквы и закодировал ими. Буквы ФЧШЩ не использовал.
- [1, 1, 5, 5, 7] Добавил все буквы. Уже стало несколько лучше, но всё равно есть числа, которые нельзя закодировать, это недопустимое ухудшение.
- [1, 2, 5, 9, 16] Я до этого использовал частоту букв из интернета, а тут решил посчитать сам в корпусе, порасставлял буквы, лучше не стало.
- [0, 0, 1, 3, 5] И тут я понял теперь уже очевидную вещь. А вы догадались?
Я понял, что важна не частота встречания букв в слове в целом, а частота их нахождения на 1 и на 2 месте в слове (для кодирования двухзначных чисел). Нужно, чтобы для каждой цифры были такие буквы, чтобы вероятность найти одну из этих букв в начале или в конце слова была одинаковая.
Считаем частоты на 1 месте, на 2 месте и на 2 местах сразу:
Мне далее показалось проще скопировать вывод в табличный редактор и подобрать шифр так, чтобы частоты были максимально равномерно распределены между кодируемыми цифрами.
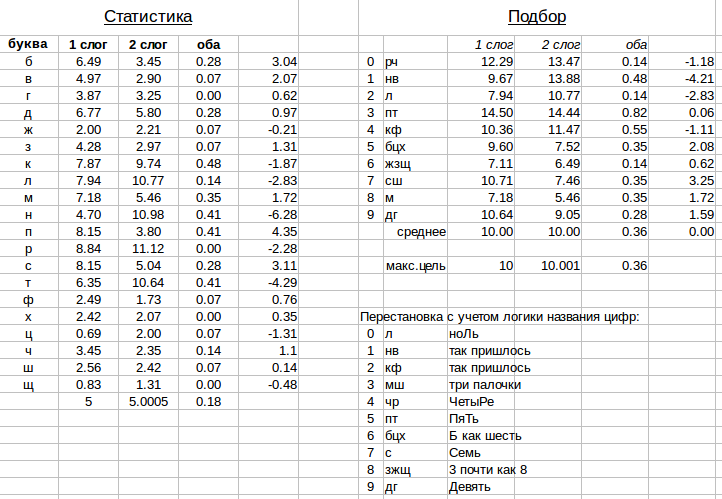
Посмотрим на результат:
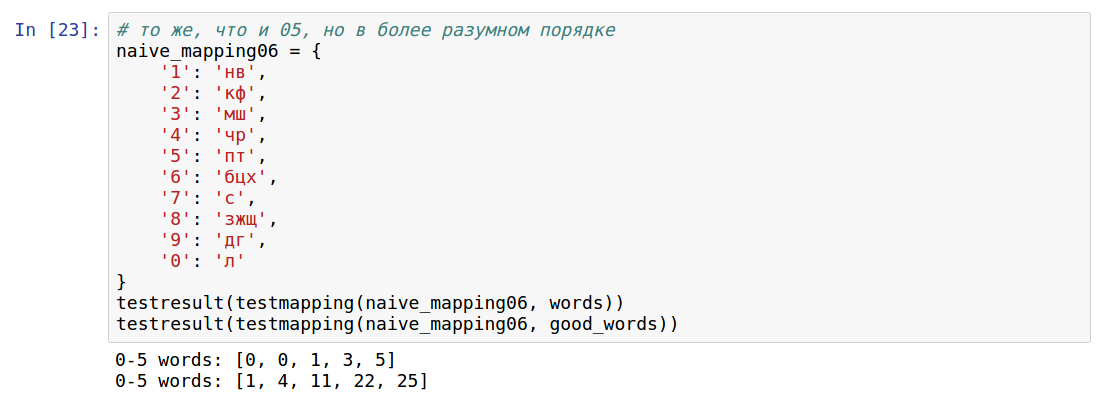
Как видно, для «простых» слов всё равно остались некодируемые буквы. Например, потому что никакое слово не содержит РР, а буквы Ч в «простых» словах не было. В итоге я решил, что правильнее считать по всем буквам.
Посмотрим на слова, которые вошли в итоговый список для некоторых чисел:
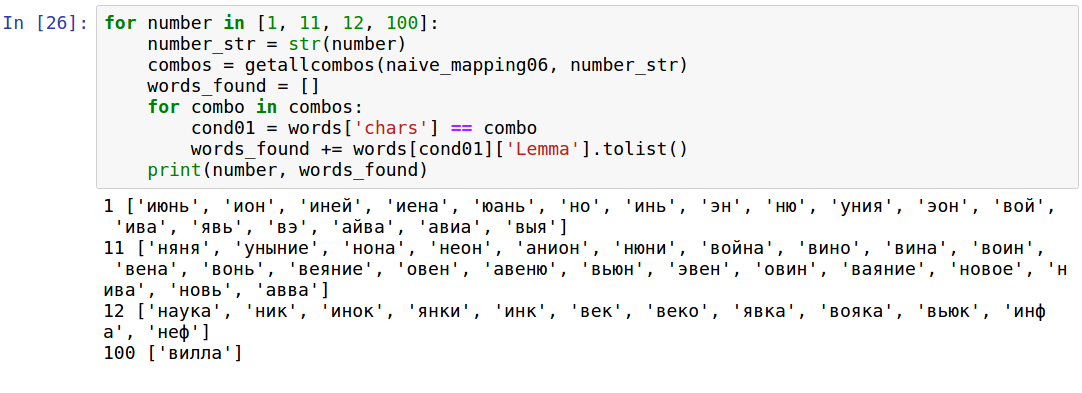
Как видно, по факту слов подходит несколько меньше. Мы не можем использовать уныние, войну, вину, вонь, веяние, новое, новь, а также слова, которых не знаем. Однако всё равно остается много хороших слов для всех чисел, в том числе трехзначных.
Код ноутбука, данные и текст статьи лежат тут: Github
Надеюсь, вам понравилось, а также буду рад советам:
- а как вы запоминаете числа?
- как сделать полный перебор допустимых вариантов мэппинга?
- как быстро освоить метод?
- про опечатки и возможные улучшения оформления статьи прошу писать в личные сообщения
