Разбор задач финального раунда RCC 2016

18-го сентября был проведен последний, финальный этап чемпионата по спортивному программированию Russian Code Cup 2016 года. Первое место в упорной борьбе занял Геннадий Короткевич, второе и третье места — Владислав Епифанов и Николай Калинин соответственно.
Турнирную таблицу финала можно найти здесь, призовой фонд в этом году впервые распределен на первые 25 мест рейтинга. Это не единственное нововведение — впервые в RCC имели возможность поучаствовать англоговорящие программисты, коих набралось более тысячи из 4.5 тысяч участников. Помимо традиционных для соревнования стран СНГ, в финальном раунде боролись представители Германии, Финляндии, Японии, Швейцарии, Китая и Южной Кореи. Кроме того, в этот раз был проведен зеркальный раунд на Codeforces — сразу после финала основного состязания, у всех желающих была возможность решить задачи финала в специально организованном соревновании для первого дивизиона, поучаствовало чуть больше 200 программистов.
Традиционно предлагаем вам разбор задач финала (тесты можно скачать здесь):
A. Церемония закрытия
B. Кактусофобия
C. Домашнее задание
D. Слалом
E. Шифр
F. Покрытие массива
A. Церемония закрытия
Ограничение по времени 2 секунды
Ограничение по памяти 256 мегабайт
Условие
Церемония закрытия Squanch Code Cup проводится в большом зале на n × m человек. Сам зал состоит из n рядов, в каждом из которых находится m стульев. Каждый стул имеет две координаты: (x, y) (1 ≤ x ≤ n, 1 ≤ y ≤ m).
На вход в зал столпилось две очереди: k человек находится в точке с координатами (0, 0), и n·m — k человек в точке с координатами (0, m + 1). У каждого человека должен быть билет на определённое место. Если у человека p с начальными координатами (x, y) билет на место (xp, yp), ему нужно будет пройти |x — xp| + |y — yp|.
Про каждого человека известна его выносливость, а именно какое максимальное расстояние он может пройти. Ваша задача узнать, можно ли распределить все билеты, чтобы каждый человек смог дойти до своего места.
Формат входных данных
Первая строка ввода содержит два натуральных числа n и m (1 ≤ n·m ≤ 104) — размеры зала.
Вторая строка содержит несколько целых неотрицательных чисел. Первое число k (0 ≤ k ≤ n·m) обозначает число людей с начальными координатами (0, 0). За ним следуют k чисел, обозначающих выносливость этих людей.
Третья строка содержит несколько целых неотрицательных чисел. Первое число l (l = n·m — k) обозначает число людей с начальными координатами (0, m + 1) За ним следуют l чисел, обозначающих выносливость этих людей.
Выносливость задается натуральными числами, не превышающими n + m.
Формат выходных данных
Если можно распределить билеты описанным способом, выведите «YES». Иначе выведите «NO».
Примеры
Входные данные:
2 2
3 3 3 2
1 3
Выходные данные:
YES
Входные данные:
2 2
3 2 3 3
1 2
Выходные данные:
NO
Решение
Эта задача решается жадным алгоритмом. Давайте отсортируем людей из первой очереди по тому, сколько они готовы пройти. И будем их поочерёдно расставлять, выбирая каждый раз место следующим образом: среди незанятых мест, до которых он может дойти, выберем то, которое наиболее удалено от второй очереди (точки с координатами (0, m + 1)). После распределения мест для первой очереди, мы сортируем людей из второй очереди и жадно расставляем их по свободным местам, начиная с минимального.
В задаче проходили грамотно написанные решения с асимптотикой не более O((nm)2), которые соответствуют описанию этого жадного алгоритма. Если пользоваться сетом, то асимптотику можно сократить до O(nm log(nm))
B. Кактусофобия
Ограничение по времени 2 секунды
Ограничение по памяти 256 мегабайт
Условие
Дерево — это связный неориентированный граф без циклов. Реберный кактус — связный неориентированный граф без петель и кратных ребер, в котором каждое ребро лежит не более чем на одном простом цикле.
У Васи есть реберный кактус, в котором каждое ребро покрашено в какой-то цвет. Вася хочет убрать из кактуса минимальное число ребер так, чтобы получилось дерево. При этом он хочет, чтобы количество различных цветов среди оставшихся ребер было максимально. Помогите ему узнать, сколько различных цветов может остаться в графе.
Формат входных данных
В первой строке дано два целых числа n, m (2 ≤ n ≤ 10 000) — количество вершин и ребер в графе Васи соответственно.
В следующих m строках дано по три целых числа u, v, c (1 ≤ u, v ≤ n, u ≠ v, 1 ≤ c ≤ m) — вершины, которые соединяет очередное ребро, и его цвет. Гарантируется, что описанный граф является реберным кактусом.
Формат выходных данных
Выведите одно целое число — максимальное количество различных цветов, которое можно оставить в графе.
Примеры
Входные данные
4 4
1 2 4
2 3 1
3 4 2
4 2 3
Выходные данные
3
Входные данные
7 9
1 2 1
2 3 4
3 1 5
1 4 5
4 5 2
5 1 6
1 6 4
6 7 6
7 1 3
Выходные данные
6
Решение
Разобьем граф на блоки — циклы и мосты. Нужно из каждого цикла удалить одно ребро, и при этом оставить в графе максимально много различных цветов.
Построим двудольный граф, в котором левая доля — блоки, правая — цвета. Из блока проведем ребра в каждый цвет, который есть в этом блоке (если цвет встречается несколько раз, проведем несколько ребер). Из цветов ребра в сток. Из истока ребра в блок, если блок — мост, то с пропускной способностью 1, иначе с пропускной способностью на 1 меньше длины цикла. Несложно видеть, что максимальный поток в этом графе и будет являться ответом.
Еще в этой задаче есть решение, не использующее потоки, и работающее за O(n), предлагаем придумать его в качестве упражнения.
C. Домашнее задание
Ограничение по времени 3 секунды
Ограничение по памяти 256 мегабайт
Условие
Сегодня Петя плохо вел себя на уроке математики, и учительница наказала его, дав ему дополнительное домашнее задание. Она назвала ему три числа n, m и k и сказала, чтобы он отметил на прямоугольной клетчатой доске размером n × m одну или несколько клеток. Отмеченные клетки должны образовывать связную фигуру. При этом должно быть ровно k способов выбрать три отмеченные клетки так, чтобы они образовывали «уголок» — все три выбранные клетки лежали внутри квадрата 2 × 2.
Множество клеток образует связную фигуру, если из любой клетки множества можно добраться до любой другой, перемещаясь в процессе с клетки на соседнюю по стороне. Петя знает, что задание непростое, поэтому попросил вас, как программиста и лучшего друга, помочь ему с этим заданием.
Формат входных данных
Входные данные содержат несколько тестовых наборов. В первой строке задано количество тестов t (1 ≤ t ≤ 100). Каждый из следующих t тестов описывается одной строкой из трех чисел n, m и k (3 ≤ n, m, n × m ≤ 105, 0 ≤ k ≤ 109). Гарантируется, что сумма n × m по всем тестам не превосходит 105.
Формат выходных данных
Для каждого теста выведите ответ на него. Если ответ существует, выведите n строк по m символов, где '*' означает отмеченную клетку, а '.' — неотмеченную. Если ответа не существует, в единственной строке выведите -1. После каждого теста, кроме последнего, выведите пустую строку.
Примеры
Входные данные
3
3 3 4
3 3 5
3 3 3
Выходные данные
**.
**.
…
***
**.
…
.**
**.
*…
Решение
Задача решается придумыванием конструктивного алгоритма.
- Для упрощения разбора случаев для всех n, m < 5 запустим полный перебор. Здесь, чтобы избежать неасимптотических оптимизаций и уложиться в TL, стоило сделать предподсчет.
- Теперь, не умоляя общности, можем считать, что m ≥ 5.
- Начнем расставлять звездочки подряд по таблице (по строчкам сверху вниз, в каждой строке слева направо). При добавлении каждой звездочки (кроме крайних) добавляется 4 новых уголка. При добавлении звездочки в конец строки добавляется 3 новых уголка, в начало — 1. Прекращаем процесс как только k становится меньше 4 или как только свободных клеток в таблице остается меньше 5.
- Дальнейшее развитие событий делится на два случая:
- осталась свободная строка
- не осталось свободной строки
- Первый случай. Раз осталась свободная строка, значит мы прервались, потому что k стало меньше 4. Тогда:
- k = 0: ничего добавлять не надо, все сошлось
- k = 1: если в текущей строке поставлено уже ≥ 2 звездочки, поставим звездочку в начало следующей строки, а если нет, то в конец текущей
- k = 2: если в текущей строке поставлено уже ≥ 3 звездочки, поставим звездочку во второй столбец следующей строки, а если нет, то в предпоследнюю клетку текущей
- k = 3: если в текущей строке поставлено уже ≥ 4 звездочек, поставим звездочки в первый и третий столбец следующей строки. Если поставлено три, поставим во второй столбец следующей и в предпоследний текущей. Если две — в начало следующей строки и в пред-предпоследний столбец текущей. Если одна — ставим звездочки в m — 1 и m — 3 столбцы текущей строки (нумерация с нуля).
- Второй случай. В таблице осталось 4 свободных клетки, куда можно поставить звездочки. Несложным перебором случаев можно вывести, что, ставя звездочки в эти клетки, можно получить следующие значения k: {0, 1, 2, 3, 4, 5, 6, 8, 9, 12, 15}. Разбор этих случаев остается читателю в качестве упражнения.
- Также стоило не забыть про случай прямоугольника 3 × m, где m ≥ 5 и k = 2 * (m — 1) — 8 — в этом случае надо оставить первый столбец пустым, а все остальные полностью заполнить.
D. Слалом
Ограничение по времени 2 секунды
Ограничение по памяти 256 мегабайт
Условие
Девочка Маша очень любит зимние виды спорта, и сегодня ей предстоит пройти лыжный слалом. Трасса схематически представляет собой клетчатый прямоугольник n × m. На поле размещены прямоугольные препятствия, занимающие некоторые клетки. Маша должна добраться из клетки с координатами (1, 1), в клетку (n, m). При этом из каждой клетки можно перейти либо на одну клетку вверх, либо на одну клетку вправо. В клетки, в которых расположены препятствия, попадать нельзя.
Таким образом, каждое препятствие можно обойти двумя способами: оно останется либо слева от траектории движения по трассе, либо справа. Маша любит разнообразие, и ей интересно, сколько существует различных способов пройти трассу. Проходы трассы считаются различными, если существует хотя бы одно препятствие, которое в одном проходе находится слева, а в другом справа от траектории Маши.
Ваша задача — помочь Маше узнать количество различных способов пройти трассу. Ответ может быть большим и Машу устроит значение по модулю 109 + 7. На рисунках ниже разобраны тесты из условия.
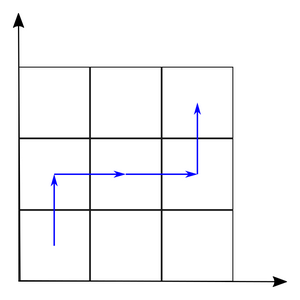

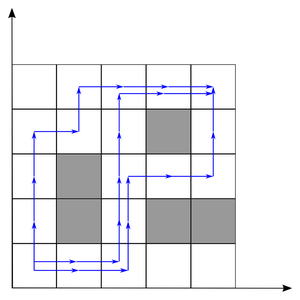
Формат входных данных
В первой строке входных данных содержатся три натуральных числа n, m и k (3 ≤ n, m ≤ 106, 0 ≤ k ≤ 105) — размеры трассы и количество препятствий соответственно. В следующих k строках находится по четыре натуральных числа x1, y1, x2, y2 (1 ≤ x1 ≤ x2 ≤ n, 1 ≤ y1 ≤ y2 ≤ m) — координаты левого нижнего и правого верхнего угла препятствия. Гарантируется, что в клетках (1, 1) и (n, m) нет препятствий, и все препятствия не имеют пересечений (но могут касаться).
Формат выходных данных
В выходной файл выведите единственное число — остаток от деления количества различных способов пройти трассу на число 109 + 7.
Примеры
Входные данные
3 3 0
Выходные данные
1
Входные данные
4 5 1
2 2 3 4
Выходные данные
2
Входные данные
5 5 3
2 2 2 3
4 2 5 2
4 4 4 4
Выходные данные
3
Решение
Для начала рассмотрим все возможные пути из начальной клетки в конечную, в которых перемещение из клетки идет либо вверх, либо вправо, а также они не пересекают препятствия. Введем понятие класса эквивалентности путей. Пути находятся в одном классе, если они не являются различными по определению из условии задачи. В данной задаче требовалось найти количество таких классов.
Решать задачу будем методом динамического программирования. Для каждого класса будем рассматривать самый нижний путь: сумма высот клеток, по которым он проходит, минимальна. Состояние динамического программирования — это количество таких нижних путей, проходящих через данную клетку. Тогда, когда мы встретим препятствие, все пути, которые проходят через клетки ниже его верха, могут разделится на два, если выше них нет другого препятствия, которое помешает это сделать. То есть при обработке препятствия в клетку над его верхней границей надо добавить сумму значений по клеткам ниже его верха, пути из которых имеют возможность разделиться.
Наивная реализация этого алгоритма требовала O(nm) памяти и O(nm2) времени, поэтому надо использовать дерево отрезков для оптимизации подсчета суммы при переходах динамического программирования, а также хранить не все поле, а только текущий столбец. Таким образом получается O(m) памяти, и время работы составляет O(n log m).
E. Шифр
Ограничение по времени 2 секунды
Ограничение по памяти 256 мегабайт
Условие
Недавно Боря увидел большое электронное табло. На табло зашифровано некоторое число. Само число состоит из n разрядов, каждый из которых записан с помощью маленькой латинской буквы. Рядом с табло находится табличка, которая описывает схему шифрования. Так для каждого разряда i и цифры j известен символ c, которым она кодируется. При этом разным цифрам могут соответствовать одинаковые буквы. Каждую секунду число, которое кодируется на табло, увеличивается на один. А через секунду после того, как все n цифр числа, зашифрованного на табло, оказываются равны девяти, табло издает очень громкий звук.
Андрей знает, какое число было зашифровано на табло в самом начале. Ему стало интересно, через сколько секунд Боря сможет точно определить это число. Считайте, что Боря абсолютно точно может замерять время, а также, что первый раз число на табло поменяется ровно через секунду после того, как Боря увидел табло.
Формат входных данных
В первой строке задано целое число t (1 ≤ t ≤ 100) — количество тестовых примеров. Описание каждого теста начинается с числа n (1 ≤ n ≤ 18) — количества символов в зашифрованном числе. В следующей строке записано n цифр без пробелов (возможно, с ведущими нулями) — зашифрованное число. В следующих n строках записано по десять символов. Если j-й символ в строке i равен c, то цифра j — 1 в i-м разряде (более старшие разряды описаны раньше) кодируется буквой c.
Формат выходных данных
Для каждого тестового примера в отдельной строке выведите одно целое число без ведущих нулей — минимальное количество секунд, которое необходимо, чтобы расшифровать число.
Примеры
Входные данные
3
2
42
abcdefghij
jihgfedcba
2
42
aaaaaaaaaa
aaaaaaaaaa
1
2
abcdabcdff
Выходные данные
0
58
2
Решение
Для начала рассмотрим решение, которое находит правильный ответ, но работает долго. Что обозначает, что Боря точно может определить, какое число было изначально? Это значит, что он может отличить его от любого другого числа. Поэтому рассмотрим все другие числа и для каждого найдем первый момент времени, когда его можно будет отличить от заданого. Для этого сравним, как кодируются два числа в первый момент времени. Если они кодируются одинаковым образом, то добавим к каждому единицу и сравним еще раз. Будем так продолжать пока два числа не будут кодироваться по-разному. Если вдруг одно из чисел не помещается на табло, то по условию задачи Боря об этом узнает из-за громкого звука, и значит в этот момент сможет отличить его.
Основная идея решения заключается в том, что нам не нужно проверять, что число можно отличить от всех 10n — 1 других. Утверждается, что если мы можем отличить число от такого же, в котором изменили ровно одну цифру, то можем отличить и от всех других чисел. Таким образом, необходимо узнать первый момент времени, когда можно отличить число от 9n других.
Заметим, что эту подзадачу тоже можно решать быстрее чем за 10n. Для этого переберем разряд, по которому можно будет отличить два числа, а также его значение. После этого найдем первый момент времени, когда одно из чисел примет именно такое значение и проверим, можем ли отличить два числа. Таким образом, получаем решение, которое работает за полиномиальное от количества цифр время.
F. Покрытие массива
Ограничение по времени 3 секунды
Ограничение по памяти 256 мегабайт
Условие
У Миши есть массив из n целых чисел. Он хочет выбрать k различных подотрезков в нем так, чтобы для каждого элемента массива нашелся хотя бы один выбранный отрезок, который его содержит. При этом Миша хочет, чтобы если просуммировать числа на каждом отрезке, а затем просуммировать получившиеся суммы, то итоговая сумма оказалась максимальна.
Формат входных данных
В первой строке дано два целых числа n, k (1 ≤ n ≤ 100 000, 1 ≤ k ≤ n·(n + 1) / 2) — количество элементов в массиве и количество отрезков, которые нужно выбрать.
Во второй строке дано n целых чисел ai ( — 50 000 ≤ ai ≤ 50 000) — элементы массива.
Формат выходных данных
Выведите одно целое число — максимальную сумму сумм чисел на отрезках, которую можно достичь, выбрав k отрезков так, что каждый элемент был покрыт хотя бы одним отрезком.
Примеры
Входные данные
5 4
6 -4 -10 -4 7
Выходные данные
11
Решение
Для начала заметим, что в ответ обязательно войдут min(k — n, 0) максимальных по сумме отрезков. Для решения задачи найдем сумму min(k — n, 0) максимальных отрезков и элементы, которые они покрывают, а также следующие за ними min(k, n) отрезков в явном виде. Сделать это можно с помощью бинарного поиска по значению суммы на отрезке и структуры данных вроде дерева Фенвика: для заданного значения суммы дерево Фенвика поможет найти и количество отрезков с хотя бы такой суммой, и сумму отрезков с хотя бы такой суммой, и множество покрытых элементов, и перечислить все отрезки с такой суммой за их количество. Эту часть решения можно сделать за O(n log2 n).
Немного отвлечемся. Рассмотрим, как можно решать задачу за n2 log n. Пускай мы перебрали x — количество максимальных по сумме отрезков в ответе (O(n) вариантов, поскольку min(k — n, 0) максимальных отрезков войдут в ответ обязательно). Пусть элементы с индексами i1, …, im остались непокрыты, и нужно их покрыть используя k — x отрезков. Заметим, что каждый из этих k — x отрезков обязан содержать хотя бы один ij-й, причем два отрезка не могут пересекаться по какому-нибудь ij-му. Можно отсортировать эти k — x отрезков лексикографически, и если l-й отрезок покрывает число ij, а l + 1-й отрезок покрывает ij + 1, то эти два отрезка либо пересекаются по какому-то подотрезку отрезка [ij + 1; ij + 1 — 1], либо не пересекаются по какому-то подотрезку отрезка [ij + 1; ij + 1 — 1]. Таким образом, если для каждого отрезка [ij + 1; ij + 1 — 1] выписать число, равное максимуму из его максимального подотрезка и минус минимального, то наилучшее покрытие — взять весь массив, но не взять минимальный префикс (до i1), минимальный суффикс (от im), и k — x максимальных чисел среди выписанных. Таким образом, решили задачу за n2 log n.
Чтобы соптимизировать это решение, можно хранить отрезки [ij + 1; ij + 1 — 1] в упорядоченном множестве. При добавлении нового максимального отрезка нужно удалить несколько ij-х, пересчитать в сете максимальные и минимальные подотрезки для затронутых отрезков (это можно сделать за O(1), зная максимальную сумму на префиксе и суффиксе подотрезка), и взять сумму k — x максимальных чисел из множества. Суммарно удалений ij-х O(n), поэтому вся эта часть работает за O(n log n).
***
Чемпионат Russian Code Cup входит в число инициатив Mail.Ru Group, направленных на развитие российской IT-отрасли и объединённых ресурсом IT.Mail.Ru. Платформа IT.Mail.Ru создана для тех, кто увлекается IT и стремится профессионально развиваться в этой сфере. Проект объединяет чемпионаты Russian AI Cup, Russian Code Cup и Russian Developers Cup, образовательные проекты Технопарк в МГТУ им. Баумана, Техносфера в МГУ им. М.В. Ломоносова и Технотрек в МФТИ. Кроме того, на IT.Mail.Ru можно с помощью тестов проверить свои знания по популярным языкам программирования, узнать важные новости из мира IT, посетить или посмотреть трансляции с профильных мероприятий и лекции на IT-тематику.
Комментарии (1)
20 сентября 2016 в 11:42
–2↑
↓
>Mail.Ru Group
Самая сложная задача: написать однострочник на Perl удаляющий Амиго.
