Разбираемся в ROC и AUC
Привет, Хабр!
В машинном обучение очень важны метрики оценки эффективности моделей. Среди таких метрик есть: кривые ROC и показатель AUC. Они позволяют оценивать бинарные классификаторы.
Кривая ROC — это график, который иллюстрирует производительность классификационной модели при всех возможных порогах классификации. Ось X данного графика представляет собой FPR, т.е ложноположительную частоту, а ось Y — TRP, т.е истинноположительную частоту. TPR также известен как Recall, и определяется как доля правильно классифицированных положительных результатов относительно всех положительных результатов в данных:
где TP — истинно положительные результаты, а FN — ложно отрицательные результаты.
FPR определяет долю ошибочно классифицированных отрицательных результатов относительно всех отрицательных результатов и вычисляется как:
где FP — ложноположительные результаты, а TN — истинно отрицательные результаты.
Кривая ROC представляет собой графическое представление компромисса между чувствительностью и специфичностью при различных порогах классификации. Идеальная модель классификации будет стремиться к точке в верхнем левом углу графика, где TPR равно 1, а FPR равно 0.
Показатель AUC (Area Under the ROC Curve) — это мера, которая позволяет суммировать производительность модели одним числом, измеряя площадь под кривой ROC. AUC колеблется от 0 до 1, где более высокое значение AUC указывает на более высокую производительность модели. AUC равный 0.5 указывает на отсутствие дискриминационной способности модели, тогда как AUC равный 1.0 означает идеальное различие классов.
Важные свойства AUC — это инвариантность к порогу классификации и масштабу предсказаний. Инвариантность к масштабу предсказаний означает, что AUC не зависит от масштаба вероятностей, которые генерирует модель. Например, две модели могут выдавать предсказания в различных масштабах, одна — в виде вероятностей от 0 до 1, а другая — в виде более широкого диапазона значений. Несмотря на эти различия, AUC будет одинаковым, если порядок ранжирования случаев от наиболее вероятного положительного до наиболее вероятного отрицательного сохраняется.
Построение кривой ROC на Питоне
Прежде всего, необходимо подготовить данные и обучить модель. Например, можно использовать логистическую регрессию для бинарной классификации. Сначала импортируем необходимые библиотеки и загружаем данные:
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
import matplotlib.pyplot as plt
# загрузка данных
url = "https://raw.githubusercontent.com/Statology/Python-Guides/main/default.csv"
data = pd.read_csv(url)
X = data[['student', 'balance', 'income']]
y = data['default']
# разделение данных на обучающую и тестовую выборки
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)Затем обучаем модель и делаем предсказания вероятностей:
# инициализация и обучение модели
log_regression = LogisticRegression()
log_regression.fit(X_train, y_train)
# предсказание вероятностей
y_pred_proba = log_regression.predict_proba(X_test)[:,1]Для расчета значений TPR и FPR используем функцию roc_curve, а затем строим кривую:
fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)
# построение ROC кривой
plt.plot(fpr, tpr)
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()Для оценки качества модели расчитаем площадь под ROC кривой, используя roc_auc_score:
auc = metrics.roc_auc_score(y_test, y_pred_proba)
print("AUC: %.3f" % auc)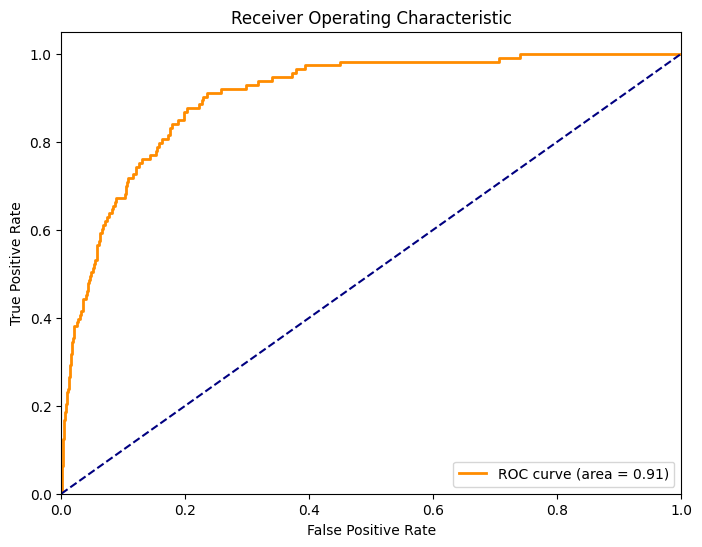
Дополним интерактивную визуализации с помощью plotly вместо matplotlib, что позволит добавить интерактивные элементы на график.
import plotly.graph_objs as go
trace = go.Scatter(x=fpr, y=tpr, mode='lines', name='AUC = %0.2f' % auc,
line=dict(color='darkorange', width=2))
reference_line = go.Scatter(x=[0,1], y=[0,1], mode='lines', name='Reference Line',
line=dict(color='navy', width=2, dash='dash'))
fig = go.Figure(data=[trace, reference_line])
fig.update_layout(title='Interactive ROC Curve',
xaxis_title='False Positive Rate',
yaxis_title='True Positive Rate')
fig.show()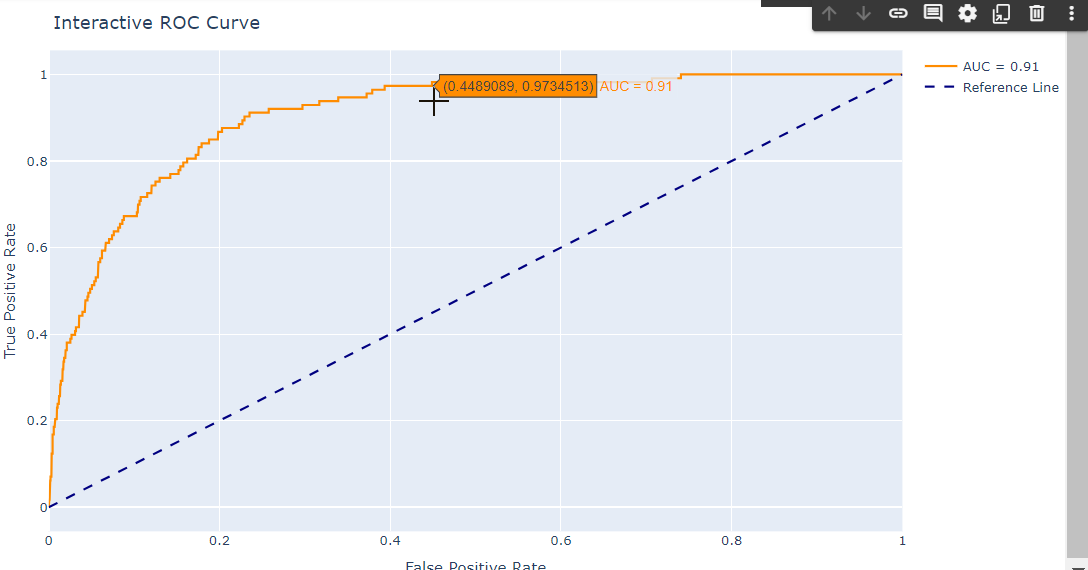
Полный код
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
import matplotlib.pyplot as plt
# Загрузка данных
url = "https://raw.githubusercontent.com/Statology/Python-Guides/main/default.csv"
data = pd.read_csv(url)
X = data[['student', 'balance', 'income']]
y = data['default']
# Разделение данных на обучающую и тестовую выборки
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# Инициализация и обучение модели
log_regression = LogisticRegression()
log_regression.fit(X_train, y_train)
# Предсказание вероятностей
y_pred_proba = log_regression.predict_proba(X_test)[:,1]
# Расчет ROC кривой
fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)
auc = metrics.roc_auc_score(y_test, y_pred_proba)
# Построение ROC кривой
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()
# Интерактивная визуализация с Plotly
import plotly.graph_objs as go
trace = go.Scatter(x=fpr, y=tpr, mode='lines', name='AUC = %0.2f' % auc,
line=dict(color='darkorange', width=2))
reference_line = go.Scatter(x=[0, 1], y=[0, 1], mode='lines', name='Reference Line',
line=dict(color='navy', width=2, dash='dash'))
fig = go.Figure(data=[trace, reference_line])
fig.update_layout(title='Interactive ROC Curve',
xaxis_title='False Positive Rate',
yaxis_title='True Positive Rate',
margin=dict(l=40, r=0, t=40, b=30))
fig.show()
Интерпретация кривой ROC и выбор порога классификации
Кривая ROC строится с TPR по оси Y и FPR по оси X для различных пороговых значений. Чем ближе кривая находится к верхнему левому углу графика, тем лучше производительность модели. Идеальный классификатор будет проходить через верхний левый угол (TPR = 1, FPR = 0), что означает высокую чувствительность и низкую частоту ложных срабатываний. Диагональная линия, проходящая через график, представляет собой классификатор, который не лучше случайного угадывания.
Оптимальное пороговое значение зависит от контекста задачи и баланса между TPR и FPR, который считается приемлемым. Например, в мед. диагностике может быть важнее минимизировать количество ложноотрицательных результатов (высокий TPR), даже за счет увеличения количества ложноположительных результатов (высокий FPR). Порог выбирается там, где кривая ROC касается линии, которая проведена из левого нижнего угла (FPR = 0, TPR = 0) к точке на кривой, которая обеспечивает баланс между чувствительностью и специфичностью.
Значение AUC как мы ранее говорили, лежит в диапазоне от 0 до 1, где 1 соответствует идеальному классификатору, а 0.5 — классификатору, работающему не лучше случайного угадывания. Высокое значение AUC указывает на то, что модель хорошо различает классы при различных порогах.
При использовании ROC кривой и AUC часто возникают ошибки, которые могут привести к неправильной интерпретации производительности классификационной модели (ну, без ошибок никак).
Одной из основных ошибок при использовании AUC является игнорирование влияния несбалансированных классов. Когда один класс значительно превышает другой по количеству примеров, модель может быть смещена в сторону большего класса, что влияет на TPR и FPR.
Способ минимизации:
Использование методов балансировки классов, таких как взвешивание классов в процессе обучения, использование техник пересэмплирования (oversampling меньшего класса и undersampling большего класса).
Рассмотрение других метрик в дополнение к AUC, таких как точность, полнота и F-мера, которые могут дать более полную картину при несбалансированных классах.
AUC часто интерпретируется как вероятность того, что случайно выбранный положительный пример будет оценен моделью выше, чем случайно выбранный отрицательный пример. Ошибка заключается в том, что высокий AUC не всегда указывает на высокую эффективность модели во всех ситуациях, особенно если классы сильно несбалансированы.
Способ минимизации:
Использование комбинированных подходов при оценке модели, включая анализ ROC кривой для определения оптимального порога классификации, который обеспечивает приемлемый баланс между TPR и FPR.
Рассмотрение структуры данных и специфики задачи при интерпретации AUC.
При использовании ROC кривой важно помнить, что ее форма зависит от выбора порогового значения классификации, что может привести к ошибочным выводам о производительности модели, особенно если порог выбран неоптимально.
Способ минимизации:
Изучение ROC кривой для разных порогов, чтобы понять, как изменение порога влияет на TPR и FPR.
Выбор порога, который обеспечивает наилучший компромисс между обнаружением положительных и отрицательных случаев в соответствии с бизнес-целями и затратами на ошибки.
Применение ROC и AUC в многоклассовых сценариях может быть затруднено, поскольку классические определения TPR и FPR предназначены для бинарной классификации.
Способ минимизации:
Применение метода one-vs-all или one-vs-one для расчета ROC и AUC для каждой пары классов в многоклассовой задаче.
Использование микро- или макро-усреднения для агрегации метрик.
Больше метрик и практических инструментов мои коллеги из OTUS рассматривают в рамках практических онлайн курсов. Переходите в каталог и выбирайте подходящее направление.
